一种构造逆标签及其损失函数的方法与流程

本发明属于深度学习与人工智能
技术领域：
，特别是一种基于逆标签的损失函数构造方法。
背景技术：
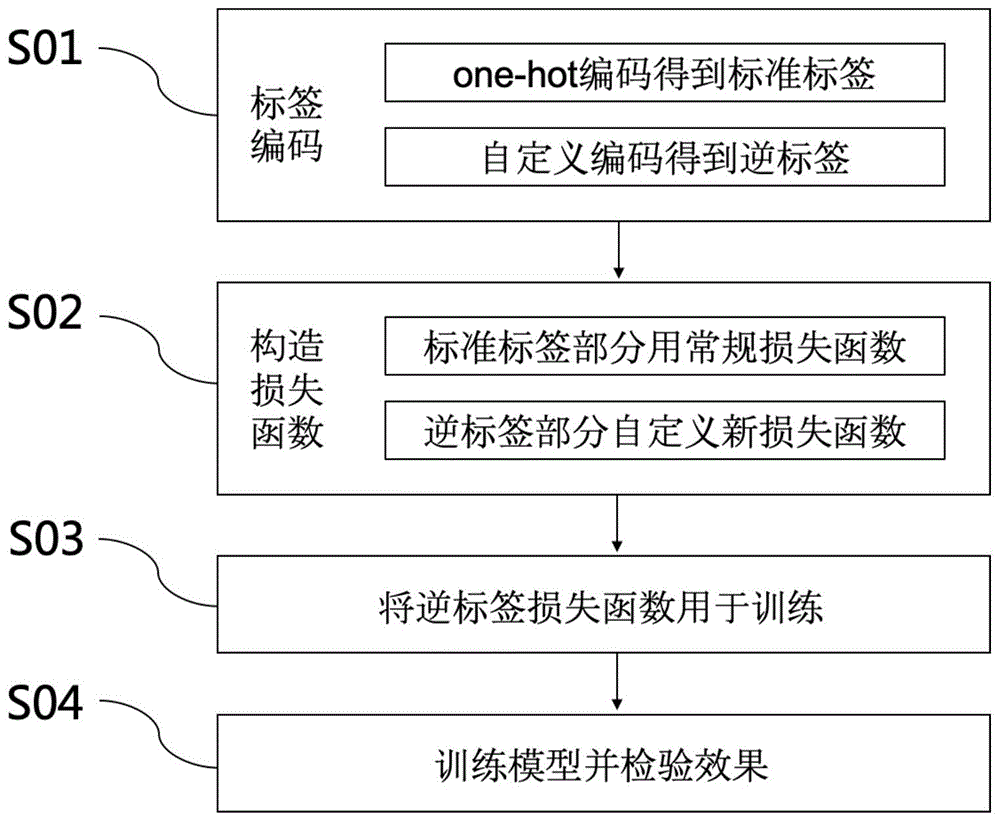
：分类问题，尤其是图像分类问题，是深度学习领域最重要，也是最常见的问题之一，目标是判断给定图像所属的类别。解决这类问题的一般方式为，构造一个卷积神经网络，网络通常由多个卷积层和全链接层构成，前者提取图像特征，后者进行分类任务，训练时将图像做预处理后输入网络，最后一层通常与类别数量一致，对应为各个类别上的概率，该概率向量与标签向量通过损失函数计算损失函数值，并反向求导，更新参数，以此不断迭代。一般损失函数的设计，只针对one-hot编码形式的标签向量，反向求导过程中，也只在标签类别对应位置上产生负的梯度，这类方法仅考虑标签位置的信息，而忽略了非标签位置的信息。技术实现要素：本发明的目的在于提供的一种构造逆标签及其损失函数的方法，实现了对非标签位置信息的利用，达到提高模型分类性能的目的。本发明的目的可以通过以下技术方案实现：一种构造逆标签及其损失函数的方法，包括如下步骤：步骤s01、对类别标签进行编码：对类别标签分别用one-hot编码产生标准标签向量和用自定义编码产生的逆标签向量；步骤s02、构造逆标签损失函数：逆标签损失函数由步骤s01中产生的标准标签和逆标签分别构造标准标签函数和逆标签函数，将标准标签函数和逆标签函数进行加权求和，即得到逆标签损失函数；步骤s03、将逆标签损失函数用于训练：设定步骤s02中逆标签损失函数的参数k，将参数k代入逆标签损失函数，并将逆标签损失函数代入实际应用场景，获得模型；步骤s04、训练模型并检验效果：训练模型得到一个分类器，用该分类器对新样本进行预测并检验效果。进一步地，所述步骤s1中标签编码包括常规one-hot编码和逆标签编码，one-hot编码将原始类别标签转化为标准标签向量，标准标签向量的形式为(0,0,…,1,…,0,0)，向量长度等于类别数量n，原标签对应位置为1，其他n-1个位置均为0；自定义编码方式将原类别标签转化为逆标签向量，所述逆标签的向量的形式为(1/n’,1/n’,…,0,…,1/n’,1/n’)，向量长度等于类别数量n，与标准标签相反，原标签对应位置为0，其他n-1个位置均为1/n’，n’等于n-1。进一步地，所述步骤s02中逆标签损失函数的计算公式为invloss＝celoss+k×inverselabelloss，参数k用于调节两部分比重，是超参数，其中，yi为标准标签第i个分量，pi为预测概率向量的第i个分量，zi为逆标签第i个分量。进一步地，所述参数k在不同应用场景下对应的数值不同。进一步地，所述步骤s04中，所述训练模型的性能采用如下定义的类别间马氏距离来度量，计算包括以下步骤：步骤t01、计算两类别中心位置，具体为求各个维度上的平均值，得到中心点，分别记为a、b；步骤t02、分别计算两类别方差和协方差矩阵，具体以步骤t01得到的中心点为均值，计算该类别全部样本到该中心点的方差，分别记为sigmaa、sigmab，及协方差矩阵，分别记为cova、covb；步骤t03、取两中心点a、b间的某一“中点”c，使得c点到a、b两点的马氏距离相同，为了方便计算，这一步可简化为ac与bc长度比值等于sigmaa、sigmab的比值；步骤t04、分别计算ac与bc的马氏距离，ac马氏距离用cova计算，bc马氏距离用covb计算；步骤t05、ac与bc的马氏距离相加即得到两类别间的马氏距离。本发明的有益效果：本发明提供的一构造逆标签及其损失函数的方法，通过对样本赋予逆标签，对标签信息进行了更为丰富发掘与利用，并设计相应的损失函数，与常规损失函数相结合，使得训练过程不仅产生标签位置的负的梯度，也产生非标签位置的正的梯度，达到增强原有损失函数训练能力、提升模型分类性能的效果。附图说明为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。图1为本发明中一种构造逆标签及其损失函数的方法的示意图；图2为本发明中逆标签产生过程的示意图；图3为本发明中构造权重系数的示意图；图4为本发明中计算两类别间距离的示意图。图5为本发明实施例中的样本图像。具体实施方式下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其它实施例，都属于本发明保护的范围。请参阅图1所示，一种构造逆标签及其损失函数的方法，包括如下步骤：步骤s01、对类别标签进行编码：对类别标签分别用one-hot编码产生标准标签向量和用自定义编码产生逆标签向量。请参阅图2所示，标签编码包括常规one-hot编码和逆标签编码，one-hot编码将原始类别标签转化为标准标签向量，标准标签向量的形式为(0,0,…,1,…,0,0)，向量长度等于类别数量n，原标签对应位置为1，其他n-1个位置均为0；自定义编码方式将原类别标签转化为逆标签向量，所述逆标签的向量的形式为(1/n’,1/n’,…,0,…,1/n’,1/n’)，向量长度等于类别数量，与标准标签相反，原标签对应位置为0，其他n-1个位置均为1/n’，其中，n’等于n-1，保证各位置数值求和等于1，如图2所示，例如，类别数量为5，对于一个标签为2的样本，标准标签产生过程为，生成一个5维向量，第2维度为1，其他维度为0，逆标签产生过程为，生成一个5维向量，第2维度为0，其他维度为1/(5-1)即1/4，即类别数量为5产生的标签向量为(0,1,0,0,0),逆标签向量为(1/4,0,1/4,1/4,1/4)；步骤s02、构造逆标签损失函数：逆标签损失函数由步骤s01中产生的标准标签和逆标签分别构造标准标签函数和逆标签函数，将标准标签函数和逆标签函数进行加权求和，即得到逆标签损失函数。标准标签部分直接使用现有的损失函数，如交叉熵损失(crossentropyloss)，作为标准标签函数，记作celoss，见公式(1)，其中，yi为标准标签第i个分量，pi为预测概率向量的第i个分量，该概率向量为模型输出结果，在训练过程中随着参数的更新不断变化，希望通过损失函数调节的部分；逆标签部分构造逆标签函数，记作inverselabelloss，见公式(2)，目的是其具有良好的求导性质，其中，zi为逆标签第i个分量，pi为预测概率向量的第i个分量；将标准标签函数和逆标签函数相加得到逆标签损失函数invloss，见公式(3)，其中，参数k用于调节两部分比重，是超参数；invloss＝celoss+k×inverselabelloss(3)步骤s03、将逆标签损失函数用于训练：设定步骤s02中逆标签损失函数的参数k，将参数k代入逆标签损失函数，并将逆标签损失函数代入实际应用场景，获得模型。请参阅图3所示，参数k有多种设定方式：1)方式一，在训练过程中保持恒定，一般设置在0.01，这种方式适用于加载预训练参数的模型，这种模型的特点是已经加载了模型在大型数据集上训练的参数，在初始就具有较好的特征提取能力，表现出较高的分类准确率；2)方式二，在训练过程中呈阶段性上升，如图3方式二中1-30轮训练为0，31-60轮训练为0.002，61-90轮训练为0.005，90-100轮训练为0.009，这种方式适用于没有加载预训练参数，且学习速度较慢的模型，前期准确率低仅使用交叉熵作为损失函数使其快速学习，后期逐步增强逆标签信息作为调节，使得学习过程更加稳健；3)方式三，在训练过程中逐步上升，从0开始，每个轮训练均匀增加k的值，结束时达到0.15左右，这种方式适用于没有加载预训练参数，且学习速度较快的模型，模型在初始准确率较低的情况下仅使用交叉熵损失以便快速学习，随着准确率的快速上升，逆标签信息也逐渐增强。具体模型的选择及训练参数的设定由实际应用场景决定。这一过程分为两个部分，首先选择或设计一个分类模型，图像分类任务中一般使用卷积神经网络，如vgg、resnet，然后选择训练方式并设定相关参数，包括损失函数、优化器、终止条件等，形成训练框架。步骤s04、训练模型并检验效果：训练模型得到一个分类器，用该分类器对新样本进行预测并检验效果。将实际应用场景中的数据输入步骤s03中搭建的训练框架，开启训练直至结束，得到参数已经训练好的模型，即分类器，其中，应用场景中的数据输入可为人脸识别问题中的人脸图像及其标签或医疗问题中的病情特征及其标签等。至此，整个学习过程结束，分类器可用于实际生产生活中，实现对新样本的预测。另外，为了检验分类器的性能，比较用普通交叉熵损失函数训练的分类器和用逆标签损失函数训练的分类器的优劣，通过类别间的马氏距离来衡量两分类器间的分类间隔，分类间隔越大，模型准确率、鲁棒性等性能越好。请参阅图4所示，马氏距离计算的是点与点之间的距离，通过计算类别间间距检验模型效果，两类别间的间距通过计算两类别中心的马氏距离来度量，两类别距离计算包括以下步骤：步骤t01、计算两类别中心位置，具体为求各个维度上的平均值，得到中心点，分别记为a、b；步骤t02、分别计算两类别方差和协方差矩阵，具体以步骤t01得到的中心点为均值，计算该类别全部样本到该中心点的方差，分别记为sigmaa、sigmab，及协方差矩阵，分别记为cova、covb；步骤t03、取两中心点a、b间的某一“中点”c，使得c点到a、b两点的马氏距离相同，为了方便计算，这一步可简化为ac与bc长度比值等于sigmaa、sigmab的比值；步骤t04、分别计算ac与bc的马氏距离，ac马氏距离用cova计算，bc马氏距离用covb计算；步骤t05、ac与bc的马氏距离相加即得到两类别间的马氏距离。具体实施方法为，将模型最后一层输出作为预测标签，通过分类器对新样本的预测得到众多新样本的预测标签，将每一个预测标签看作空间中的一个点，即得到众多新样本在预测空间中的分布。空间中每个类别的样本看作一个簇，计算各个簇即各个类别间的马氏距离，如计算类别1和类别2间的距离，并对两两类别间的距离取平均，即得到最终的分类间隔。对要进行比较的多个分类器求分类间隔，比较数值，数值越大，则分类器性能越好。实施例一：以糖尿病视网膜病变数据集(diabeticretinopathy)为例展示逆标签构建过程。该数据的病变情况有5种：没有病变(nodr)、轻微病变(mild)、中度病变(moderate)、严重病变(severe)、增殖性病变(proliferativedr)，分别记为0、1、2、3、4。图5所示的样本为该数据集中命名为9992_right的样本，该样本的病变级别为1，以该样本为例展示逆标签构造过程。步骤s01对病变级别即标签进行编码：1)标准one-hot编码：y＝[0,1,0,0,0]2)逆标签编码：z＝[1/4,0,1/4,1/4,1/4]步骤s02计算损失函数：不失一般性设定权重系数k为1，网络输出的向量p＝[0.1,0.5,0.3,0.05,0.05]，则invloss＝celoss+k×inverselabelloss＝0.693+1×0.026＝0.719步骤s03将逆标签损失函数用于训练：在深度学习模型中，使用逆标签损失作为损失函数。步骤s04训练模型并检验效果：对设定好的模型进行训练，并检验效果。为了衡量模型分类性能，可以计算自定义的类别间马氏距离，以类别“没有病变(nodr)”和类别“轻微病变(mild)”之间的距离为例，计算过程如下：步骤t01、对两类别的全部样本求均值得到两类别中心，不失一般性假定两类别中心分别为：a＝[5.253,2.377,1.044,-2.709,-6.415]b＝[-0.406,2.974,2.580,-0.998,-4.625]步骤t02、计算两类别方差和协方差矩阵，分别为：sigmaa＝7.59sigmab＝15.45cova＝[[3.38,-0.292,0.023,-1.133,-2.084],[-0.292,0.706,-0.058,-0.395,0.088],[0.023,-0.058,0.629,-0.106,-0.518],[-1.133,-0.395,-0.106,0.907,0.707],[-2.084,0.088,-0.518,0.707,1.974]]covb＝[[9.318,-0.178,-2.604,-3.004,-3.565],[-0.178,1.222,-0.065,-0.57,-0.503],[-2.604,-0.065,1.291,0.717,0.663],[-3.004,-0.57,0.717,1.47,1.411],[-3.565,-0.503,0.663,1.411,2.167]]步骤t03、找到“中点”c使得ac与bc的马氏距离相等：步骤t04、计算ac与bc的马氏距离之和即为两类别间的马氏距离：表1交叉熵损失函数与逆标签损失函数的结果对比错误率分类间隔交叉熵损失函数16.52％2.358逆标签损失函数15.93％2.478由表1可知，使用逆标签损失函数训练的模型具有更大的分类间隔，针对疾病定级问题，可以降低预测错误结果的偏离度；引入逆标签损失函数，学习算法在训练过程中更容易收敛到类别区分度更大的解，使得错误下降率达到了(16.52％-15.93％)/16.52％＝3.57％，显著降低了预测错误率。以上内容仅仅是对本发明的构思所作的举例和说明，所属本
技术领域：
的技术人员对所描述的具体实施例做各种各样的修改或补充或采用类似的方式替代，只要不偏离发明的构思或者超越本权利要求书所定义的范围，均应属于本发明的保护范围。当前第1页1 2 3