一种二氧化碳压裂过程中井筒温度的预测方法与流程

本发明属于石油地球物理勘探领域，涉及一种预测砂岩含烃储层的测井解释方法与装置。

背景技术：

页岩气co2压裂可以实现储层增产、提高页岩气采收率以及co2埋存三重目标，具有广阔的应用前景。co2压裂过程中，井筒内温度的变化会直接影响co2的携砂能力和造缝性能，并最终影响储层改造效果，因此有必要对井筒温度场进行模拟预测。

井筒温度场解析模型计算效率高，无稳定性和收敛性的限制，可用于工程上快速估算井筒温度场。常用的井筒温度场解析解为hasan和kabir提出的解析模型，但hasan模型针对采气井建立，在物理过程中注重采出而非注入，在求解方法上注重慢速流动的长期采气过程而非快速流动的短期压裂过程，无法适用于压裂过程，因此尚缺少针对co2压裂过程的井筒温度预测的方法。

技术实现要素：

本发明的目的在于提供能够实现快速进行二氧化碳压裂过程中井筒温度预测的方法，且该方法的预测结果相对准确。

为了实现上述目的，本发明提供了一种二氧化碳压裂过程井筒温度的预测方法，该方法包括：

1)获取参数；

2)基于获取的参数，计算在二氧化碳压裂过程井筒的待预测位置在待预测时间的具体温度，从而实现二氧化碳压裂过程中井筒温度的预测；计算所用公式为：

其中，

式中，tf为井筒温度即co2温度，℃；tsurf为地表温度，℃；gg为地温梯度，℃/m；z为待预测位置的井筒斜深即在井筒轴线方向上待预测位置距离地表的距离，m；θ为井筒与水平面夹角；△t为入口初始温度与入口流入温度之差即地表温度与注入温度之差，℃；t为待预测时间即待预测时间点距离co2压裂过程开始时间点的时间间隔，s；v为井筒内co2压裂液的流速，m/s；ct为热存储系数；φ为集总参数，℃/m；lr为松弛距离参数，1/m；cpf为co2压裂液的比热容，j/(kg·℃)。

上述二氧化碳压裂过程井筒温度的预测方法，既可以实现井筒某一位置在压裂过程中特定时间的温度预测；也可以实现井筒某一位置在整个压裂过程中的温度变化即分别预测待预测位置在压裂过程中各个时间点的温度；还可以预测在压裂过程中某某时间点井筒温度场分布即分别预测在压裂过程中某个时间点井筒各处的温度；还可以预测整个压裂过程的井筒温度场分布即分别预测在压裂过程的各个时间点井筒各处的温度。其中，井筒的位置以其所处的深度进行区分。

在上述二氧化碳压裂过程井筒温度的预测方法中，优选地，所述参数包括地表温度、地温梯度、松弛距离参数、井筒内co2压裂液的流速(井筒内co2压裂液的流速可以通过co2压裂液的施工排量结合井筒管径计算得到)、集总参数、热存储系数、井筒轴向与水平面夹角、地层深度即井筒斜深、待预测时间、co2压裂液的注入温度。

在上述二氧化碳压裂过程井筒温度的预测方法中，优选地，所述松弛距离参数lr满足如下公式：

式中：

其中，rto为油管外半径，m；rh为水泥环外半径，m；rco为套管外半径，m；rti为油管内半径，m；rci为套管内半径，m；cpf为co2压裂液的比热容，j/(kg·℃)；cpe为岩石比热容，j/(kg·℃)；cpan为环空比热容，j/(kg·℃)；λh为水泥环导热系数，w/(m·℃)；λan为环空导热系数，w/(m·℃)；λe为岩石导热系数，w/(m·℃)；ρe为岩石密度，kg/m³；ρan为环空密度，kg/m³；gr为格拉晓夫数，无因次；pran为环空区域普朗特数用于计算环空换热系数han；βan为环空流体热膨胀系数，1/℃；μan为环空流体粘度，pa·s；tc为套管温度，℃；w为井筒内co2压裂液的质量流量，kg/s；han为环空流体对流传热系数，w/(m²·℃)。

在上述二氧化碳压裂过程井筒温度的预测方法中，优选地，所述参数包括地层深度即井筒斜深、井筒内co2压裂液的质量流量、co2压裂液的注入温度、油管内径、油管外径、套管内径、套管外径、水泥环外径、环空密度、岩石密度、地表温度、地温梯度、环空比热容、岩石比热容、环空导热系数、水泥环导热系数、岩石导热系数、环空流体粘度、环空流体热膨胀系数、井筒内co2压裂液的流速、co2压裂液的密度、co2压裂液的比热容、集总参数、热存储系数、井筒轴向与水平面夹角、待预测时间。

在一具体实施方式中，上述二氧化碳压裂过程井筒温度的预测方法优选包括：

1)获取参数，所述参数包括地层深度即井筒斜深、co2压裂液的施工排量(co2压裂液的施工排量结合二氧化碳压裂液的密度确定井筒内co2压裂液的质量流量，计算得到co2压裂液的施工排量结合井筒管径能够确定井筒内co2压裂液的流速)、co2压裂液的注入温度、油管内径、油管外径、套管内径、套管外径、水泥环外径、环空密度、岩石密度、地表温度、地温梯度、环空比热容、水泥环比热容、岩石比热容、油管导热系数、套管导热系数、环空导热系数、水泥环导热系数、岩石导热系数、环空流体粘度、环空流体热膨胀系数、co2压裂液密度、co2压裂液的比热容、集总参数、热存储系数、井筒轴向与水平面夹角、待预测时间；

2)基于获取的参数，计算在二氧化碳压裂过程井筒的待预测位置在待预测时间的具体温度，从而实现二氧化碳压裂过程井筒温度的预测；计算所用公式为：

其中，

a＝vlr/[1+ct]，单位：1/s；

b＝a/lr，单位：m/s；

c＝bψ，单位：℃/s；

式中，tf为井筒温度即co2温度，℃；tsurf为地表温度，℃；gg为地温梯度，℃/m；z为待预测位置的井筒斜深，m；θ为井筒轴向与水平面夹角；△t为入口初始温度与入口流入温度之差即地表温度与co2压裂液的注入温度之差，℃；t为待预测时间，s；v为井筒内co2压裂液的流速，m/s；ct为热存储系数；φ为集总参数，℃/m；lr为松弛距离参数，1/m；rto为油管外半径，m；rh为水泥环外半径，m；rco为套管外半径，m；rti为油管内半径，m；rci为套管内半径，m；cpf为co2压裂液的比热容，j/(kg·℃)；cpe为岩石比热容，j/(kg·℃)；cpan为环空比热容，j/(kg·℃)；λh为水泥环导热系数，w/(m·℃)；λan为环空导热系数，w/(m·℃)；λe为岩石导热系数，w/(m·℃)；ρe为岩石密度，kg/m³；ρan为环空密度，kg/m³；gr为格拉晓夫数，无因次；pran为环空区域普朗特数用于计算环空换热系数han；βan为环空流体热膨胀系数，1/℃；μan为环空流体粘度，pa·s；tc为套管温度，℃；w为井筒内co2压裂液的质量流量，kg/s；han为环空流体对流传热系数，w/(m²·℃)。

在上述二氧化碳压裂过程井筒温度的预测方法中，优选地，步骤2)计算在二氧化碳压裂过程井筒的待预测位置在待预测时间的具体温度采用迭代法进行。在一具体实施方式中，在具体计算过程中uto的确定包括：步骤1：假设uto值为utos；步骤2：计算td；步骤3：计算th，tci，gr，pr，han；步骤4：计算uto；步骤5：判断|uto-utos|＜err，如为真则结束迭代，如为假则将uto赋值给utos后重复步骤2-步骤5；其中，tf的初始值即为原始地层温度，也即为tf＝tsurf+gg·z·sinθ。

在上述二氧化碳压裂过程井筒温度的预测方法中，优选地，迭代法的温度收敛条件为两迭代步之间温度差值绝对值小于0.01。

在上述二氧化碳压裂过程井筒温度的预测方法中，优选地，所述集总参数满足如下公式其中p为压裂液压力，pa。

在上述二氧化碳压裂过程井筒温度的预测方法中，co2压裂液的流速和/或二氧化碳压裂液的质量流量可以利用施工排量结合二氧化碳压裂液的密度以及管径计算得到。

本发明提供的co2压裂井井筒温度场的预测方法能够实现快速准确的估算co2压裂井井筒温度场。

附图说明

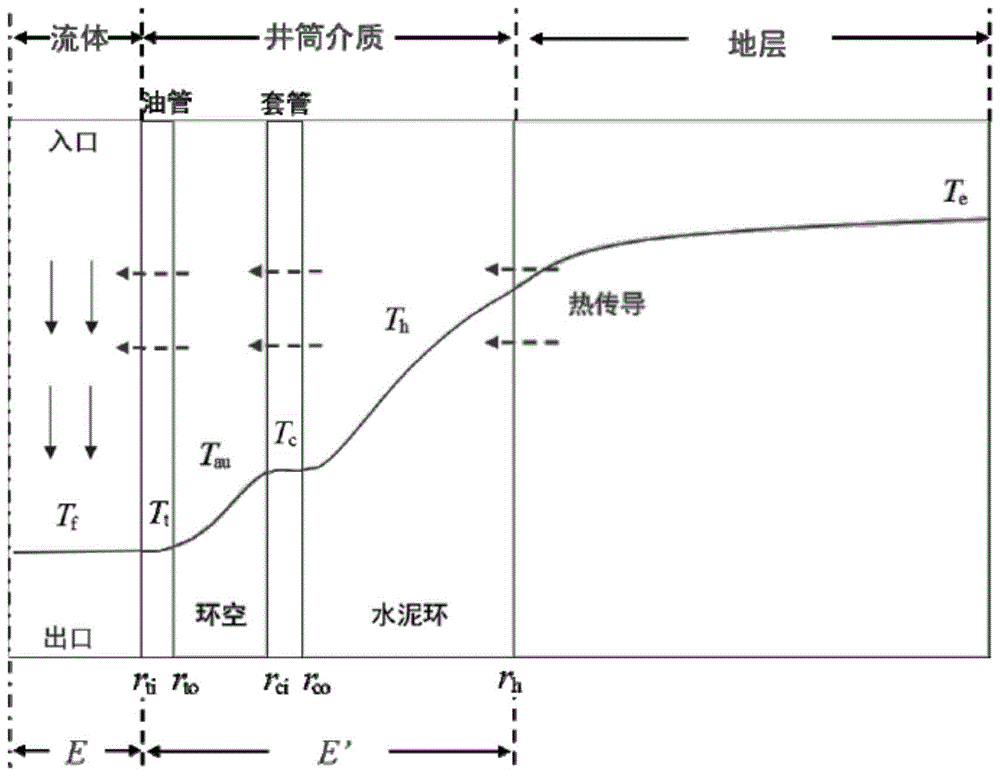
图1为压裂过程中井筒与地层温度场物理模型示意图。

图2为实施例1、对比例1、对比例2中采用不同方法预测co2压裂井施工120min时的井筒温度场图。

图3为实施例2、对比例3、对比例4中采用不同方法预测co2压裂井施工过程中井底温度变化图。

具体实施方式

为了对本发明的技术特征、目的和有益效果有更加清楚的理解，现对本发明的技术方案进行以下详细说明，但不能理解为对本发明的可实施范围的限定。

某油田xx井为直井，其进行co2压裂的具体井筒参数和岩石物理性质测试数据等请参见表1；在co2压裂过程中，具体施工排量为6m³/min，二氧化碳相关参数请参见表2。下述实施例1-2以及对比例1-4分别预测该井在co2压裂过程中井筒温度的情况。压裂过程中井筒与地层温度场物理模型示意图如图1所示。

表1

表2

其中，集总参数定义为：式中p为压裂液压力，pa。

实施例1

本实施例提供一种co2压裂过程中井筒温度的预测方法，该方法包括：

1)获取参数，所述参数包括井筒斜深、co2压裂液的注入温度、油管内径、油管外径、套管内径、套管外径、水泥环外径、环空密度、岩石密度、地表温度、地温梯度、环空比热容、岩石比热容、环空导热系数、水泥环导热系数、岩石导热系数、环空流体粘度、环空流体热膨胀系数、井筒内co2压裂液的流速、井筒内压裂液的质量流量，co2压裂液密度、co2压裂液比热容、集总参数、热存储系数、井筒轴向与水平面夹角、待预测时间(120min即7200s)；

2)基于获取参数计算在co2压裂过程进行到第120min时，井筒各位置的温度的分布情况(结果请参见图2)，从而实现co2压裂井井筒温度的预测；计算所用公式为：

其中，

a＝vlr/[1+ct]，单位：1/s；

b＝a/lr，单位：m/s；

c＝bψ，单位：℃/s；

式中，tf为井筒温度，℃；tsurf为地表温度，℃；gg为地温梯度，℃/m；z为待预测位置的井筒斜深，m；θ为井筒轴向与水平面夹角；△t为入口初始温度与入口流入温度之差即地表温度与注入温度之差，℃(此处为20℃)；t为待预测时间，s(进行到第120min则t取120×6＝7200s)；v为流速，m/s；ct为热存储系数；φ为集总参数，℃/m；lr为松弛距离参数，1/m；rto为油管外半径，m；rh为水泥环外半径，m；rco为套管外半径，m；rti为油管内半径，m；rci为套管内半径，m；cpf为co2压裂液的比热容，j/(kg·℃)；cpe为岩石比热容，j/(kg·℃)；cpan为环空比热容，j/(kg·℃)；λh为水泥环导热系数，w/(m·℃)；λan为环空导热系数，w/(m·℃)；λe为岩石导热系数，w/(m·℃)；ρe为岩石密度，kg/m³；ρan为环空密度，kg/m³；gr为格拉晓夫数，无因次；pran为环空区域普朗特数用于计算环空换热系数han；βan为环空流体热膨胀系数，1/℃；μan为环空流体粘度，pa·s；tc为套管温度，℃；w为井筒内co2压裂液的质量流量，kg/s；han为环空流体对流传热系数，w/(m²·℃)。

其中，步骤2)采用迭代法进行计算，tf的初始值为原始地层温度也即为tf＝tsurf+gg·z·sinθ，温度收敛条件为两迭代步之间温度差值绝对值小于0.01。

实施例2

本实施例提供一种co2压裂过程中井筒温度的预测方法，该方法具体过程以及涉及参数与实施例1相同，其区别仅在于，本实施例提供的预测方法计算在co2压裂过程中，井底位置的井筒温度的变化情况(结果请参见图3)。

对比例1

本对比例提供一种co2压裂过程中井筒温度的预测方法，该方法采用hasan解析方法对在co2压裂过程进行到第120min时，井筒各位置的温度的分布情况进行预测；其具体过程如下：

1)获取参数，所述参数包括井筒斜深、co2压裂液的注入温度、油管内径、油管外径、套管内径、套管外径、水泥环外径、环空密度、岩石密度、地表温度、地温梯度、环空比热容、岩石比热容、环空导热系数、水泥环导热系数、岩石导热系数、环空流体粘度、环空流体热膨胀系数、井筒内co2压裂液的流速、井筒内压裂液的质量流量，co2压裂液密度、co2压裂液比热容、集总参数、热存储系数、井筒轴向与水平面夹角、待预测时间(120min即7200s)；

2)基于获取参数计算在co2压裂过程进行到第120min时，井筒各位置的温度的分布情况(结果请参见图2)，从而实现co2压裂井井筒温度的预测；计算所用公式为：

其中，

式中，tf为井筒温度，℃；tsurf为地表温度，℃；gg为地温梯度，℃/m；z为待预测位置的井筒斜深，m；θ为井筒轴向与水平面夹角；△t为入口初始温度与入口流入温度之差即地表温度与注入温度之差，℃(此处为20℃)；t为待预测时间，s(进行到第120min则t取120×6＝7200s)；v为流速，m/s；ct为热存储系数；φ为集总参数，℃/m；lr为松弛距离参数，1/m；rco为套管外半径，m；rti为油管内半径，m；rci为套管内半径，m；cpf为co2压裂液的比热容，j/(kg·℃)；cpe为岩石比热容，j/(kg·℃)；cpan为环空比热容，j/(kg·℃)；λh为水泥环导热系数，w/(m·℃)；λan为环空导热系数，w/(m·℃)；λe为岩石导热系数，w/(m·℃)；ρe为岩石密度，kg/m³；ρan为环空密度，kg/m³；gr为格拉晓夫数，无因次；pran为环空区域普朗特数用于计算环空换热系数han；βan为环空流体热膨胀系数，1/℃；μan为环空流体粘度，pa·s；tc为套管温度，℃；w为井筒内co2压裂液的质量流量，kg/s；han为环空流体对流传热系数，w/(m²·℃)。

其中，步骤2)采用迭代法进行计算，tf的初始值为原始地层温度也即为tf＝tsurf+gg·z·sinθ，温度收敛条件为两迭代步之间温度差值绝对值小于0.01。

对比例2

本对比例提供一种co2压裂过程中井筒温度的预测方法，该方法采用数值方法对在co2压裂过程进行到第120min时，井筒各位置的温度的分布情况进行预测；其具体过程如下：

1、获取参数，所述参数包括井筒斜深、co2压裂液的注入温度、油管内径、油管外径、套管内径、套管外径、水泥环外径、环空密度、岩石密度、地表温度、地温梯度、环空比热容、岩石比热容、环空导热系数、水泥环导热系数、岩石导热系数、环空流体粘度、环空流体热膨胀系数、井筒内co2压裂液的流速、井筒内压裂液的质量流量，co2压裂液密度、co2压裂液比热容、集总参数、热存储系数、井筒轴向与水平面夹角、待预测时间(120min即7200s)；

2、对能量方程采用隐式迎风格式进行离散，得到离散方程为：

其中

式中，tf为井筒温度，℃；tsurf为地表温度，℃；gg为地温梯度，℃/m；z为待预测位置的井筒斜深，m；θ为井筒轴向与水平面夹角；△t为入口初始温度与入口流入温度之差即地表温度与注入温度之差，℃(此处为20℃)；t为待预测时间，s(进行到第120min则t取120×6＝7200s)；v为流速，m/s；ct为热存储系数；φ为集总参数，℃/m；lr为松弛距离参数，1/m；rco为套管外半径，m；rti为油管内半径，m；rci为套管内半径，m；cpf为co2压裂液的比热容，j/(kg·℃)；cpe为岩石比热容，j/(kg·℃)；cpan为环空比热容，j/(kg·℃)；λh为水泥环导热系数，w/(m·℃)；λan为环空导热系数，w/(m·℃)；λe为岩石导热系数，w/(m·℃)；ρe为岩石密度，kg/m³；ρan为环空密度，kg/m³；gr为格拉晓夫数，无因次；pran为环空区域普朗特数用于计算环空换热系数han；βan为环空流体热膨胀系数，1/℃；μan为环空流体粘度，pa·s；tc为套管温度，℃；w为井筒内co2压裂液的质量流量，kg/s；han为环空流体对流传热系数，w/(m²·℃)

3、给定入口温度为边界条件，将不同空间位置的方程组装起来可以得到下三角矩阵：

4、基于步骤1获取的参数，采用消元-迭代的方法求解步骤3中的矩阵，计算在co2压裂过程进行到第120min时，井筒各位置的温度的分布情况(结果请参见图2)，从而实现co2压裂井井筒温度的预测，计算所取时间步长为10s空间步长为10m。

对比例3

本对比例提供一种co2压裂过程中井筒温度的预测方法，该方法具体过程以及涉及参数与对比例1相同，其区别仅在于，本对比例提供的预测方法计算在co2压裂过程中，井底位置的井筒温度的变化情况(结果请参见图3)。

对比例4

本对比例提供一种co2压裂过程中井筒温度的预测方法，该方法具体过程以及涉及参数与对比例2相同，其区别仅在于，本对比例提供的预测方法计算在co2压裂过程中，井底位置的井筒温度的变化情况(结果请参见图3)。

对比对实施例1、对比例1及对比例2的结果，即将本发明提供的预测方法的预测结果与使用数值方法和hasan解析方法预测的预测结果进行对比。在空间域上，不同方法计算的120min时的井温剖面如图2所示，可以看出使用hasan解析方法进行预测与使用数值方法进行预测的预测结果偏差较大，而是用本发明提供的方法进行预测与使用数值方法进行预测的预测结果基本一致：施工120min后井温剖面最大偏差小于0.75℃。

对比对实施例2、对比例3及对比例4的结果，即将本发明提供的预测方法的预测结果与使用数值方法和hasan解析方法预测的预测结果进行对比。在时域上，井底温度随时间的变化如图3所示。由于使用hasan解析方法进行预测，采用了稳态假设计算温度梯度，使得非稳态方程中受温度梯度控制的对流传热效率被低估，导致使用hasan方法预测的井底温度随时间的变化率明显小于使用数值方法进行预测的预测结果，而采用本发明提供的方法预测的井底温度随时间变化趋势与采用数值方法预测的结果基本一致。

在空间域和时域上，本发明提供的预测方法与采用数值方法预测的结果相符，然而采用本申请提供的方法进行预测，大大降低了预测难度，提升了预测效率，更有益于实现快速准确的预测二氧化碳压裂过程的井筒温度。