基于稀疏表示和图像融合的高光谱图像超分辨率重建方法与流程

本发明涉及高光谱成像技术领域，具体涉及高光谱图像超分辨率的重建方法。

背景技术：

由于不同物理材料对光谱吸收不同，在某个特定波段下图像对某个缺陷会有较显著的反映，因此高光谱图像可以更准确地区分视觉上相似的物体。该特性有助于提高许多计算机视觉任务的性能，包括军事监视、目标探测等。然而，受限于成像传感技术、信噪比等因素的影响，光学系统难以获得既具有高光谱分辨率，又具有高空间分辨率的图像。

为了增强高光谱图像的空间分辨率，以进一步提高高光谱成像的应用范围，通常会采用图像融合方法或单幅图像超分辨率方法，从观测到的低分辨率图像中重建出不失真的高分辨率图像。常用的图像融合方法容易受到光谱失真的影响，使得输出图像难以保持准确的光谱信息。单幅图像超分辨率方法由于不能够获得足够的先验信息，空间分辨率提升有限。

近年来，有研究提出了一些基于深度学习的生成高分辨率高光谱图像的方法，这些方法主要通过额外的训练数据，以学习低空间分辨率图像和高空间分辨率图像之间的端到端映射，由于映射功能对于使用不同传感器采集的图像不相同，因此这些方法可能导致严重的光谱失真。

技术实现要素：

本发明提供一种基于稀疏表示和图像融合的高光谱图像超分辨率重建方法，通过将来自多光谱图像的空间信息与相同场景下增强过的高光谱图像融合，以生成高分辨率的高光谱图像。

一种基于稀疏表示和图像融合的高光谱图像超分辨率重建方法，包括：

基于函数的字典学习。采用近似赫维赛得函数(approximatedheavisidefunction，ahf)稀疏表示方法，重建出高分辨率的高光谱图像；

多光谱图像与高光谱图像映射关系学习。应用局部混合图像融合算法，将重建得到的所述高分辨率的高光谱图像与高分辨率多光谱图像融合，得到高分辨率高光谱图像

进一步地，本发明所提供的方法，可以在计算前，先将3d图像展开为2d矩阵，以便于计算，所述矩阵的行表示给定像素的光谱反射率，列表示特定光谱带中的完整图像。图像2d表示如下：

x^h∈r^wh×l，x∈r^wh×l，c^h∈r^wh×l。

进一步地，所述图像2d矩阵xh及x可以近似的表示为光谱字典基原子的线性组合：

x^h＝ψha，x＝ψla，

其中，ψ为光谱字典，a为对应的稀疏表示系数。ψl及ψh由近似赫维赛得函数生成，利用所述近似赫维赛得函数稀疏表示方法，可以计算得到粗略稀疏表示系数。

进一步地，可采用多尺度优化算法，通过多步迭代扩展图像，获取精细稀疏表示系数。

进一步地，所述多光谱图像与高光谱图像映射关系学习，可以是计算变换矩阵t∈r^l×l，以最终计算得到x＝tc。

本发明提供的采用近似赫维赛得函数稀疏表示方法，无需任何额外信息，可以将图像放大到任意尺寸，且能较好的保证光谱信息的准确性，同时，局部混合图像融合方法可以快速实现并行处理，极大的提高了运算效率。基于本发明提供的方法获取高分辨率高光谱图像，可以更高的保留高光谱图像的空间结构，同时更好的恢复细粒度纹理及粗粒度结构。

附图说明

为进一步阐明本发明的各实施例的以上和其它优点和特征，将参考附图来呈现本发明的各实施例的更具体的描述。可以理解，这些附图只描绘本发明的典型实施例，因此将不被认为是对其范围的限制。在附图中，为了清楚明了，相同或相应的部件将用相同或类似的标记表示。

图1示出根据本发明的一个实施例的一种基于稀疏表示和图像融合的高光谱图像超分辨率重建方法流程；

图2a及图2b示出本发明的一个实施例的基于近似赫维赛得函数稀疏表示方法的效果图；

图3a至图3e示出基于cave数据集中的一幅图像，使用本发明的一个实施例与其他方法所得的重建图像的效果对比示意图；以及

图4示出基于cave数据集中的另两幅图像，使用本发明的一个实施例与其他方法所得的重建图像的效果对比示意图。

具体实施方式

在以下的描述中，参考各实施例对本发明进行描述。然而，本领域的技术人员将认识到可在没有一个或多个特定细节的情况下或者与其它替换和/或附加方法、材料或组件一起实施各实施例。在其它情形中，未示出或未详细描述公知的结构、材料或操作以免模糊本发明的发明点。类似地，为了解释的目的，阐述了特定数量、材料和配置，以便提供对本发明的实施例的全面理解。然而，本发明并不限于这些特定细节。此外，应理解附图中示出的各实施例是说明性表示且不一定按正确比例绘制。

在本说明书中，对“一个实施例”或“该实施例”的引用意味着结合该实施例描述的特定特征、结构或特性被包括在本发明的至少一个实施例中。在本说明书各处中出现的短语“在一个实施例中”并不一定全部指代同一实施例。

需要说明的是，本发明的实施例以特定顺序对工艺步骤进行描述，然而这只是为了阐述该具体实施例，而不是限定各步骤的先后顺序。相反，在本发明的不同实施例中，可根据工艺的调节来调整各步骤的先后顺序。

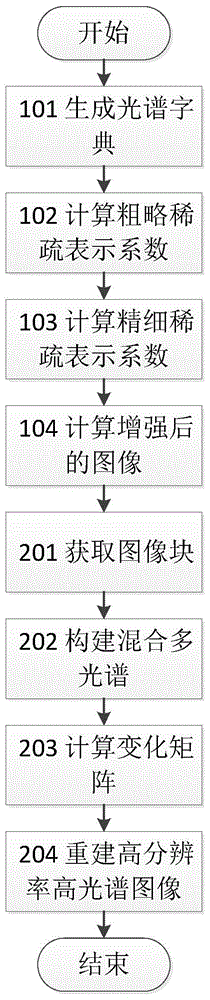
如图1所示，一种基于稀疏表示和图像融合的高光谱图像超分辨率重建方法，包括：

步骤101，生成光谱字典，

基于ahf，生成光谱字典ψ∈r^l.t，所述光谱字典的每一列表示图像中不同材料的反射光谱，定义ahf为：

其中ξ∈r，控制平滑度，取值越小，边缘越锐利；

将所述ahf扩展到二维空间，假设基础图像强度f定义在[0,1]²上，即f∈lp([0,1]²),p∈[1,∞),则f可以近似表示为：

其中，wj∈r,vj∈r²,cj∈r,

vj＝{(cosθt,sinθt)′,t＝1,2,…,k}表示k个不同方向，表示离散位置，其中m＝kq,z＝(x,y)′,q为输入图像的总像素数；

步骤102，计算粗略稀疏表示系数ac，解决优化问题s.t.‖a‖0<t,以获得粗略稀疏表示系数ac，其中a∈r^t，

通过采用增强拉格朗日乘数，将l1范数作为正则项，将所述问题转换为其中λ为加权参数，用以权衡稀疏性及重建误差；

粗略稀疏表示系数

步骤103，计算精细稀疏表示系数af，

通过多尺度优化算法提高超分辨率重建效果：

xⁱ＝x^i-1-dψa^i-1，

其中，d为下采样算子，x⁰＝x，a⁰＝ac，

则，精细稀疏表示系数其中k为迭代次数。

步骤104，计算增强后的图像，

xe＝ψaf；

结合图2，第一幅图像为低分辨率的ahf图像块，第二幅图像为高分辨率的ahf图像块；

步骤201，获取图像块，为充分利用图像的空间相关性，在图像块上执行局部混合图像融合方法，图像块ci的大小为p×p，其间可以重叠。对每一个图像块执行步骤202及步骤203；

步骤202，构建混合多光谱chi，

考虑到观测图像因受到大气影响而产生误差，将值为1的白像素与多光谱波段融合在一起，创建一个混合多光谱chi，

chi＝[ci(1),…,ci(3),1]^t

步骤203，计算变换矩阵ti，

ti＝xeichi^t(chichi^t+λi)^-1，

其中λ为正则化参数，i是与chichi^t具有相同尺寸的单位矩阵；

步骤204，重建高分辨率高光谱图像xh＝tc。

为进一步说明本发明的效果，结合图3及图4，具体描述本发明的实施方法：

选取cave数据集及harvard数据集中的高光谱图像作为实施对象：

首先，对于harvard数据集，取其左上角1024×1024大小的图像作为待处理图像，cave数据集保持不变。将处理过的这两个数据集作为高分辨率参考图像，如图3a及图4中第二列图像所示，用以比对重建结果；

接下来，通过高斯模糊和降采样处理得到输入的低分辨率图像，其中高斯模糊核的尺寸为5×5，行和列方向上的降采样因子为2，低分辨率高光谱图像如图3b及图4中第一列图像所示；

接下来，在近似赫维赛得稀疏表示方法中，将θt在[0,2π]上等间距采样选取16个角度，c从[-6,6]中等间距采样得到12个值，ξ从[0.1,10^-4]中采样，选取图像块的大小为6×6，图像块间的重叠为4，以得到精细系数矩阵af，进而得到增强的图像xe＝ψaf；

在局部混合图像融合方法中，选取图像块的尺寸为8×8，图像块间的重叠为4，计算得到变换矩阵t，进而重建高分辨率高光谱图像xh＝tc^h，如图3e及图4中第三列图像所示；

从峰值信噪比psnr、结构相似性ssim以及光谱相似度sam三个角度，将所述重建图像xh与x^h，及其他重建方法结果进行比对，其中psnr及ssim值越高表示重建效果越好，sam值越小表示光谱失真越小：

表1给出了如图3e所示的基于本发明提供的方法、如图3c所示的仅采用近似赫维赛得函数稀疏表示方法以及如图3d所示的仅采用局部混合图像融合三种方法所得到的重建图像的psnr、ssim以及sam数值对比。表2给出了基于本发明提供的方法、双三次插值法bicubic、最近邻插值法nearest以及非负结构稀疏表示方法nssr四种方法的psnr、ssim以及sam数值对比可以看出，本发明提供的超分辨率重建方法，改善了psnr、ssim以及sam数值，取得了更优的效果。

表1

表2。