一种基于序列Kriging代理模型的结构非梯度拓扑优化方法与流程

本发明属于结构与多学科优化设计领域，涉及一种基于序列kriging代理模型的结构非梯度拓扑优化方法。本方法适用于机械、仪器设备、航空航天等复杂装备的拓扑优化设计。

背景技术：

拓扑优化是解决结构及多学科优化材料最优布局设计问题的一种重要工具，目前主流方法包含变密度法，水平集法和渐进优化方法。这些方法大多根据具体优化问题推导伴随法灵敏度信息，采用梯度类优化算法进行求解，已经在机械、仪器、航空航天等装备的创新设计中得到成功应用。然而，实际工程中的许多问题，如碰撞、(材料、几何、接触)非线性、多场耦合等，无法得到解析灵敏度信息，且性能函数呈现多峰特性，梯度类优化算法无法获得全局最优解。

因此，现有的拓扑优化商业软件(如optistruct，tosca等)均采用变密度方法，只能解决柔顺性拓扑优化和基频最大化拓扑优化等易于推导灵敏度信息的特定问题，无法用于复杂多学科和非线性拓扑优化。本发明基于材料场级数展开，在大幅度减少拓扑优化设计变量的基础上，提出一种序列kriging代理模型优化算法，有效求解结构拓扑优化问题。本方法不需要设计灵敏度信息，大大降低了求解拓扑优化问题的难度，并且不存在棋盘格式、网格依赖性现象，可得到边界光滑的结构拓扑，适用于多学科、多场耦合等复杂结构材料布局优化问题。

技术实现要素：

针对传统拓扑优化方法需要推导梯度信息等复杂数学运算过程和使用门槛高的缺点，本发明提供一种有效的非梯度拓扑优化方法。该方法通用性好，不需要设计灵敏度信息，可以直接应用在复杂多学科优化和多场耦合优化问题，便于与各种有限元商业和自研软件进行对接。本发明适用于机械、仪器设备及航空航天装备等领域的材料布局拓扑优化设计。

为了达到上述目的，本发明采用的技术方案为：

一种基于序列kriging代理模型的结构非梯度拓扑优化方法，主要包括设计域材料场的缩减级数展开、非梯度拓扑优化模型建立和序列kriging代理模型算法求解三部分内容，具体步骤如下：

第一步，设计域材料场的缩减级数展开

1.1)确定结构设计域，定义材料场相关性。在结构设计域中定义材料场相关函数为c(x1,x2)＝exp(-||x1-x2||²/lc²)，其中x1和x2表示任意两个观察点的空间位置，lc为相关长度，||||为2-norm范数。在结构设计域中均匀选择np个观察点，通过相关函数计算所有观察点之间的相关性，构成一个np×np维的相关矩阵。相关矩阵具有对称正定性，且对角线为1。

1.2)对步骤1.1)中的相关矩阵进行特征值分解，将特征值λj(j＝1,2,...,np)从大到小排列；保留前m阶的特征值和对应的特征向量，保留准则为：选取的特征值之和占所有特征值总和的99％-99.9％。

1.3)以缩减级数展开的形式描述材料场，即x∈ωdes，其中，ηj(j＝1,2,...,m)为材料场展开系数，λj和ψj分别为1.2)中所提取的特征值和特征向量，cd(x)为步骤1.1)中通过计算空间中任意点与观测点相关函数而构成的相关向量，ωdes表示设计域。

第二步，非梯度拓扑优化模型建立

2.1)将整个结构进行有限元网格划分，建立1.3)中材料场与设计域有限单元相对密度之间的映射关系为(e＝1,2,...,nele)，ρe为每个有限元单元的相对密度，ρmin为相对密度的下限，的heaviside映射函数，光滑参数从0到20根据设计空间的调整阶梯性增加，xe是设计域中单元的坐标，nele是设计域内有限元单元的个数。

2.2)建立连续体非梯度拓扑优化模型如下：

s.t.g(u)＝0

gk(u,ρ)≤0,(k＝1,2,...,nc)

η^twiη≤1,(i＝1,2,…,np)

其中，η为设计变量，f(u,ρ)为目标性能函数，u为通过有限元分析得到的结构响应，ρ为设计域内单元密度ρe组成的与η相关的向量。g(u)＝0为有限元平衡方程，η^twiη≤1为有界场界限约束，gk(u,ρ)≤0为其他性能或者体积约束函数，nc为约束函数的个数。

将该优化模型变换为无约束优化形式为：

其中，p0是惩罚因子，根据公式确定其取值，floor(·)表示向下取整函数。模型的无约束化处理包含其他的内惩罚和外惩罚处理方式。

第三步，序列kriging代理模型算法求解

3.1)采用自适应设计空间调整策略，结合2.2)步骤建立的无约束优化模型，构成一系列无约束子优化问题。设计空间调整策略的步骤如下：

a)根据体积约束选择初始样本点η0，使得x∈ωdes，其中，fv为允许的材料体积比。

b)确定初始子设计空间ω0＝{|η-η0|∞≤r0}，其中r0根据公式得到：

r0＝maxr

s.t.|η-η0|∞≤r

(e＝1,2,...,nele)

其中，r0代表初始设计空间的大小，||∞为无穷范数，ζ是代表材料场上下界变化的参数，取值为0.5(无体积约束)或fv(有体积约束)。

c)采用kriging代理模型优化算法求解当前第k次子优化问题，以该最优解为下一次设计空间中心ηk，确定新的子设计空间为：

ωk+1＝{|η-ηk|∞≤rk+1}(k＝0,1,2,…)

rk+1＝0.95rk

其中，k和k+1为子设计空间次数。

d)当优化结果满足收敛准则|ηk-ηk-1|∞≤0.001时，结束优化。

3.2)针对每个子优化设计问题，使用的kriging代理模型方法进行求解，步骤如下：

a)使用拉丁超立方采样随机在每个子设计域中选择100-200个初始样本。

b)组合使用期望最大准则(ei)和最小响应面准则(mp)加点，进行优化求解。

c)满足停止准则(后续加点中连续多个新增样本不能使目标函数值降低)时，子优化问题收敛。

进一步的，所述的步骤1.1)中所述的相关长度lc选取为矩形设计域短边尺寸的30％-40％。

进一步的，所述的步骤3.1)所述的在每个子设计空间中使用的kriging代理模型算法进行优化求解。优化求解的方法还包含径向基函数，支持向量机，人工神经网络等代理模型方法。

本发明的有益效果为：不需要性能函数设计灵敏度信息，适合于解决复杂多场耦合、多学科和高非线性的拓扑优化问题。该方法不仅继承了密度法拓扑优化的简单形式，还能使拓扑结构边界清晰光滑，便于集成各种商用和自研有限元软件，是一种便于推广和工程应用的拓扑优化方法。

附图说明

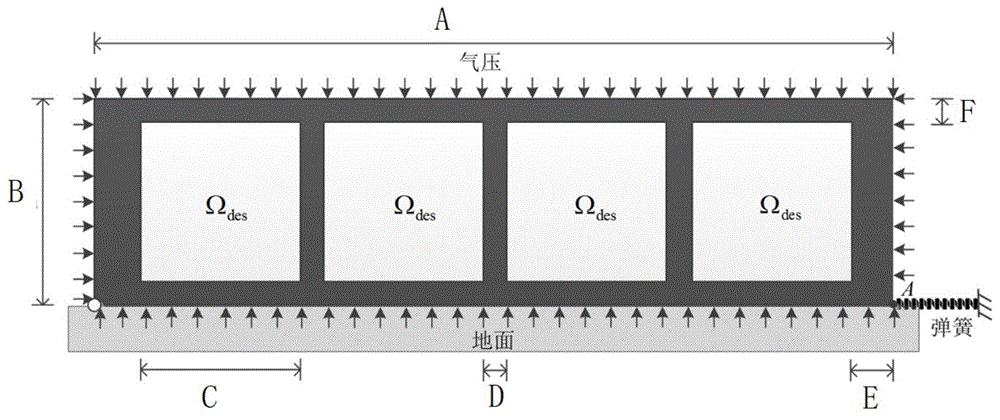
图1为本发明实施例提供的一种仿生软体机器人设计工况；图中，a：195mm；b：50mm；c：40mm；d：5mm；e：10mm；f：5mm。

图2为仿生软体机器人最优拓扑结构。

图3(a)为仿生软体机器人空心结构的位移和变形图。

图3(b)为仿生软体机器人优化后结构的位移和变形图。

具体实施方式

以下结合技术方案和附图详细叙述本发明的具体实施例。

一种基于序列kriging代理模型的结构非梯度拓扑优化方法，该拓扑优化方法通过材料场函数映射拓扑结构，并以材料场的控制参数作为设计变量。再将标准的拓扑优化模型进行无约束化处理，使用自适应设计空间调整策略和kriging代理模型方法进行求解。全过程不需要梯度信息推导，简单高效。

图1描述的是一个超弹性材料构成的仿生软体机器人优化问题，具体尺寸如图。图中40mm×40mm浅色正方形区域为结构设计域，整个结构外周受到气压作用，结构底部与地面无摩擦接触。材料属性采用3阶ogden超弹性材料。结构左下角铰支，右下角与弹簧连接。优化目标是右下角的水平位移绝对值最大化。

第一步，设计域材料场的缩减级数展开

1.1)选定相关函数和相关长度。选择相关函数c(x1,x2)＝exp(-||x1-x2||²/lc²)。在设计域中均匀选取1600个观察点，相关长度lc＝12mm。计算所有观察点之间的相关性，构成相关矩阵，相关矩阵具有对称正定性，且对角线为1。

1.2)对步骤1.1)中的相关矩阵进行特征值分解，将特征值从大到小排列。根据求解问题的精度保留前50阶的特征值和其对应的特征向量。

1.3)以缩减级数展开的形式描述材料场，即x∈ωdes，其中，ηj(j＝1,2,...,50)为材料场展开系数，λj和ψj分别为1.2)中所提取的特征值和特征向量，cd(x)为步骤1.1)中通过计算空间中任意点与观测点相关函数而构成的相关向量，ωdes表示设计域。

第二步，非梯度拓扑优化模型建立

2.1)将整个结构进行有限元网格划分，其中设计域划分为1600个单元，建立1.3)中材料场与设计域有限单元相对密度之间的映射关系为(e＝1,2,...,1600)，ρe为每个有限元单元的相对密度，ρmin＝0.001，的heaviside映射函数，光滑参数从0到20根据设计空间调整阶梯性增加，xe是设计域中单元的坐标。

2.2)以右下角位移绝对值最大化为优化目标，以相对材料体积不超过50％为约束条件，建立非梯度拓扑优化模型。并根据公式对原拓扑优化模型进行无约束化处理。

第三步，序列kriging代理模型算法求解

3.1)采用自适应设计空间调整策略，结合步骤2.2)建立的无约束优化模型，构成一系列无约束子优化问题。设计空间调整策略的步骤如下：

a)根据体积约束选择初始样本点η0，使得x∈ωdes，其中，fv＝50％。

b)确定初始子设计空间ω0＝{|η-η0|∞≤r0}，其中r0根据公式得到：

r0＝maxr

s.t.|η-η0|∞≤r

(e＝1,2,...,1600)

其中，r0代表初始设计空间的大小，||∞为无穷范数，ζ＝50％。

c)采用kriging代理模型优化算法求解当前第k次子优化问题，以该最优解为下一次设计空间中心ηk，确定新的子设计空间为：

ωk+1＝{|η-ηk|∞≤rk+1}(k＝0,1,2,…)

rk+1＝0.95rk

其中，k和k+1为子设计空间次数。

d)当优化结果满足收敛准则|ηk-ηk-1|∞≤0.001时，结束优化。

3.2)针对步骤3.1)中每个子优化设计问题，使用的kriging代理模型方法进行求解，步骤如下：

a)使用拉丁超立方采样随机在每个子设计域中选择100个初始样本。

b)组合使用期望最大准则(ei)和最小响应面准则(mp)加点，进行优化求解。

c)满足停止准则(后续加点中连续多个新增样本不能使目标函数值降低)时，子优化问题收敛。

利用带有自适应设计空间调整策略的序列kriging代理模型优化方法得到结构最优材料分布见图2。优化的拓扑构形与空心结构的位移和变形情况见图3，图3(a)中空心结构右下角位移绝对值为6.00mm，图3(b)中优化后结构角点位移绝对值为10.63mm。结果表明了优化方法的正确有效。

本发明的实质是以少量的材料场控制参数作为设计变量，拓扑优化问题采用序列kriging代理模型优化方法进行求解，不需要设计灵敏度信息。其对前述各实施例所记载的优化模型、方法、方案进行修改，或者对其中部分或者全部方法特征进行等同替换(例如采用其他设计空间调整策略、改变目标函数或约束具体形式等)，并不使相应方法与方案的本质脱离本发明各实施例方法与方案的范围。