一种用于开敞式TBM结构参数优化设计方法与流程

本发明涉及全断面岩石隧道掘进机(tunnelboringmachine，简称tbm)技术领域，具体涉及一种用于开敞式tbm结构参数优化设计方法。

背景技术：

全断面岩石隧道掘进机(tunnelboringmachine，tbm)广泛应用于轨道交通等基础设施建设中。tbm主机主要包括刀盘驱动系统和推进系统。其中，推进系统主要由支撑-推进-换步机构(gripping-thrusting-regrippingmechanism，gtrm)组成，而该机构是tbm实现连续、高效及精准掘进作业的核心传动机构，其动态性能的优劣将直接影响tbm整机的掘进效率。因此，有必要建立准确的tbm支撑-推进-换步机构动力学模型，分析机构的动态性能及其随参数的变化规律，进而为tbm动态设计与现场施工提供理论依据。

近年来，国内外学者针对tbm的结构特点及施工需求，研究了tbm支撑-推进-换步机构的动力学建模方法，并取得了一定的进展。其中，不少学者基于集中参数法建立了tbm支撑-推进-换步机构动力学模型。由于该模型具有简单、直观、实用等优点，因此被广泛应用于分析研究该类机构的动态性能，进而指导该类装备的设计与施工。与此同时，建立一个合理的模型也存在一些技术难题，例如在建模时若考虑因素较多，从而建立一个多集中参数、多自由度模型用来分析机构的动态性能，的确可以得到更加准确的计算结果，但同时也会存在以下问题：首先，考虑因素较多，会使问题变得更加复杂，将导致计算工作量增大、求解效率降低，不利于实现编程计算等等问题；其次，未能最大限度地忽略次要因素的影响，则模型直观性与实用性均会大大降低，若利用该模型来指导设计，将不利于抓住重点因素，会导致设计的盲目性，从而设计效率低；最后，当需要研究机构复杂的非线振动问题时，则必须在已有线性模型的基础之上再添加一些例如间隙、摩擦力等非线性因素，那么此时问题变得更加复杂，若不能做到简化，则可能无法得到准确收敛的结果。当前学者们在建模时考虑因素繁多，其中不乏存在较多次要因素，其中以4个集中参数的支撑-推进-换步机构动力学模型最为经典，通过实验初步证明该模型的确能够较准确地描述机构的动态特性，但同时也存在以下不足之处，即模型求解效率、直观性、实用性以及适用性等均略显不足。因此，有必要建立更加直观、实用且适用范围广的机构动力学模型，以期为后续tbm动态设计以及相关非线性振动研究提供理论基础。

技术实现要素：

针对现有技术，本发明提出一种用于开敞式tbm结构参数优化设计方法，其中建立了更加直观、实用且适用范围更广的tbm支撑-推进-换步机构动力学模型。

为了解决上述技术问题，本发明提出的一种用于开敞式tbm结构参数优化设计方法，主要包括：根据机构各构件间的刚度拓扑关系，最大限度地忽略次要因素及局部振动的影响，建立tbm支撑-推进-换步机构六自由度动力学简化模型；根据tbm支撑-推进-换步机构六自由度动力学简化模型，忽略其外部激励载荷和内部阻尼，建立机构无阻尼线性自由振动方程；基于tbm支撑-推进-换步机构无阻尼线性自由振动方程的特征值问题，求解该机构前4阶固有频率及振型，并数值仿真分析固有频率随其参数的变化规律；最后，以增大机构低阶固有频率、改善机构动态性能、提高tbm的工作效率与工作稳定性为设计目标，结合模型数值仿真结果，对tbm的结构参数进行优化。

进一步讲，本发明中，建立机构六自由度动力学简化模型的过程如下：

以水平方向为x轴方向，竖直方向为y轴方向，隧道轴向方向为z轴方向，建立坐标系xyz，选取机构质心沿x、y、z方向平移位移坐标xc、yc及zc与绕x、y及z轴轴线扭转位移坐标θcx、θcy及θcz为系统的广义坐标，利用牛顿-欧拉方法建立机构运动微分方程：

式(1)中，l1、l2、l3及l10分别代表机构质心oc与护盾总几何中心ob、推进油缸-主梁铰接点o3(o4)、撑靴几何中心o1(o2)及刀盘几何中心od沿z轴距离；l4、l7分别代表机构质心oc与推进油缸-主梁铰接点o3(o4)、撑靴几何中心o1(o2)沿x轴距离；l11、l13代表机构质心oc与刀盘几何中心od、扭矩油缸-鞍架铰接点o5(o6)沿x轴距离；l5、l6及l12分别代表机构质心oc与推进油缸-主梁铰接点o3(o4)、撑靴几何中心o1(o2)及刀盘几何中心od沿y轴距离；l8、l9分别代表破岩载荷等效作用点of与刀盘几何中心od沿y、x轴距离；r为刀盘半径；α、β分别代表推进油缸和扭矩油缸的倾斜角度；fdx(t)、fdy(t)、fdz(t)及tdz(t)分别代表滚刀破岩时沿x、y及z向等效力及绕z轴等效力矩；k1x、k2x、k3x、k4x和k1y、k2y、k3y、k4y分别代表各护盾与围岩支撑界面沿x、y向等效刚度；k6x和k6y分别代表撑靴与围岩支撑界面沿x、y向等效刚度；k5代表主梁一侧推进油缸总刚度；kn代表两侧扭矩油缸刚度；kzc代表支撑油缸刚度；ksx、ksy分别代表十字销轴沿x、y向等效刚度；kwx、kwy代表围岩沿x、y向等效刚度。

撑靴-围岩支撑界面沿x、y向等效刚度表示如下：

将机构的运动微分方程进一步整理为矩阵形式，得到：

式(3)中，u为广义坐标列阵，m为质量矩阵，k为刚度矩阵，c为瑞利阻尼矩阵，q(t)为广义激励力列阵；各矩阵的具体形式如下：

广义坐标列阵：

u＝[xcyczcθcxθcyθcz]^t(4)

质量矩阵：

m＝diag(mcmcmcjcxjcyjcz)(5)

刚度矩阵：

式(6)中，kij(i,j＝1,2,3,4,5,6)分别代表刚度矩阵各位置元素：

k11＝k1x+k2x+k3x+k4x+2k5sin²α+2k6x；k12＝0；k13＝0；k14＝0

k15＝(k1x+k2x+k3x+k4x)l1-2k5sin²αl2-2k6xl3；k16＝-k2xr+k4xr+2k5sin²αl5+2k6xl6；

k21＝0；k22＝k1y+k2y+k3y+k4y+2k6y；k23＝0；k24＝-(k1y+k2y+k3y+k4y)l1+2k6yl3；k25＝0；

k26＝(k1y-k3y)r；k31＝0；k32＝0；k33＝2k5z；k34＝-2k5zl5；k35＝0；k36＝0；

k41＝0；k42＝-(k1y+k2y+k3y+k4y)l1+2k6yl3；k43＝-2k5cos²αl5；

k44＝(k1y+k2y+k3y+k4y)l1²+2k6yl3²+2k5cos²αl5²；k45＝0；k46＝0；

k51＝(k1x+k2x+k3x+k4x)l1-2k5sin²αl2-2k6xl3；k52＝0；k53＝0；k54＝0；

k55＝(k1x+k2x+k3x+k4x)l1²+2k5sin²αl2²+2k6xl3²+2k5zl4²；k56＝0；

k61＝(-k2x+k4x)r+2k5sin²αl5+2k6xl6；k62＝(k1y-k3y)r；k63＝0；k64＝0；k65＝0；

k66＝(k2x+k4x+k1y+k3y)r²+2k5sin²αl5²+2kncos²βl13²

瑞利阻尼矩阵：

式(7)中，cij(i,j＝1,2,3,4,5,6)分别代表阻尼矩阵各位置元素；a和b均为比例阻尼系数，其取值可通过机构的基频和对振动能量贡献较大的频率值确定；

广义激励力列阵：

q(t)＝[fxfyfztxtytz]^t(8)

式(8)中，

fx＝-fdx(t)；fy＝-fdy(t)；fz＝-fdz(t)；tx＝-[fdz(t)l8-fdy(t)l10]；

ty＝-[fdz(t)l9-fdx(t)l10]；tz＝-tdz(t)。

本发明中，建立的机构无阻尼线性自由振动方程如下：

与之所对应的特征值问题为：

式(10)中，ωn、φn分别代表系统的第n阶固有频率和振型。

与现有技术相比，本发明方法的有益效果是：

(1)本发明中建立的tbm支撑-推进-换步机构动力学简化模型，其求解效率显著提高。基于机构组成及各构件间刚度拓扑关系，并在最大程度上忽略了次要因素的影响，建立机构六自由度动力学简化模型，该方法简单实用，且计算工作量小，求解效率得到显著提高。

(2)本发明中建立的tbm支撑-推进-换步机构动力学简化模型，其直观性和实用性均明显提高。tbm支撑-推进-换步机构结构较为复杂，其设计参数众多，设计时不便于抓住重点，容易导致盲目设计，设计效率低。本发明方法中所建立模型在最大程度上忽略了次要因素的影响，从而增强了模型的直观性和实用性，为后续动态特性参数影响分析奠定了基础，进而更有利于指导该类机构的动态设计。

(3)本发明中建立的tbm支撑-推进-换步机构动力学简化模型，其适用性得到提高。后续为分析机构非线性振动问题，模型中可能新增一些例如间隙、摩擦力等非线性因素，若继续采用tbm支撑-推进-换步机构多集中参数、多自由度动力学模型来研究其非线性振动问题则比较困难。然而，利用本发明方法所建立的tbm支撑-推进-换步机构一个集中参数、六自由度动力学简化模型则较好地克服了这一技术难题，适合在此模型的基础之上再添加某些非线性因素来研究机构复杂的非线性振动等问题。

综上所述，本发明方法可为该类装备的结构参数优化设计及进一步研究机构的非线性动态特性奠定良好的基础。

附图说明

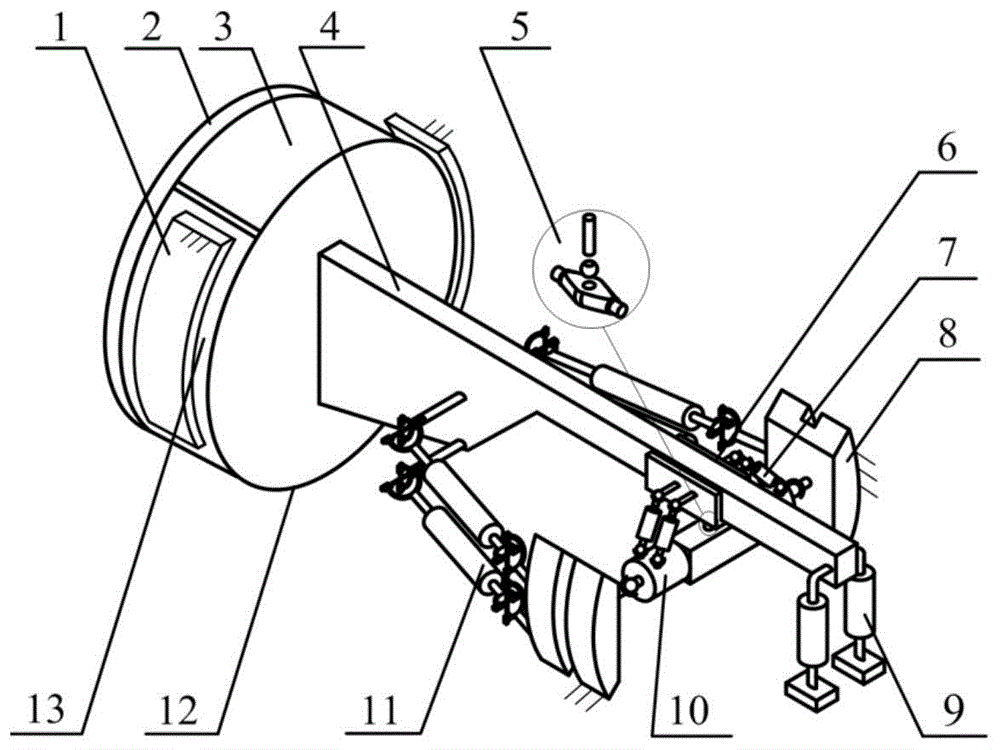
图1是本发明中涉及到的tbm支撑-推进-换步机构组成示意图；

图2是本发明中建立的动力学简化模型图；

图3(a)、图3(b)、图3(c)和图3(d)是本发明中通过动力学简化模型数值仿真得到的机构前4阶振型图，其中，图3(a)是第1阶，图3(b)是第2阶，图3(c)是第3阶，图3(d)是第4阶。

图4是本发明中通过动力学简化模型数值仿真得到的机构前4阶固有频率随扭矩油缸刚度变化的曲线图。

图5(a)、图5(b)、图5(c)和图5(d)是通过有限元模型仿真得到的机构前4阶振型图，其中，图5(a)是第1阶，图5(b)是第2阶，图5(c)是第3阶，图5(d)是第4阶。

图中：1-围岩，2-刀盘，3-顶护盾，4-主梁，5-十字销轴，6-鞍架，7-扭矩油缸，8-撑靴，9-后支腿，10-水平支撑油缸，11-推进油缸，12-底护盾，13-侧护盾。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面将结合附图和具体实施例对发明技术方案作进一步详细描述。

本发明提出的一种用于开敞式tbm结构参数优化设计方法，主要包括：根据机构各构件间的刚度拓扑关系，最大限度地忽略次要因素及局部振动的影响，建立tbm支撑-推进-换步机构六自由度动力学简化模型；根据tbm支撑-推进-换步机构六自由度动力学简化模型，忽略外部激励载荷、内部阻尼等因素，建立机构无阻尼线性自由振动方程；基于tbm支撑-推进-换步机构无阻尼线性自由振动方程的特征值问题，求解该机构前4阶固有频率及振型，并数值仿真分析固有频率随其参数的变化规律；最后，以增大机构低阶固有频率、改善机构动态性能、提高tbm的工作效率与工作稳定性为设计目标，结合模型数值仿真结果，对tbm的结构参数进行优化。

本发明的特点在于，在建立机构六自由度动力学简化模型中是根据机构各构件间的刚度拓扑关系，而且最大限度地忽略了次要因素及局部振动的影响，例如，将tbm支撑-推进-换步机构中小于整体转动惯量10％的单个质量块的转动惯量忽略不计，假设tbm支撑-推进-换步机构中的鞍架与主梁为一体，撑靴与水平支撑油缸为一体等。

下面详细说明本发明中建立tbm支撑-推进-换步机构一个集中参数、六自由度动力学简化模型的过程。

如图1所示，开敞式tbm支撑-推进-换步机构的结构是主要包括刀盘2、主梁4、鞍架6、推进油缸11、扭矩油缸7、撑靴8、水平支撑油缸10及后支腿9等，其中，刀盘2与主梁4固连，主梁4与鞍架8通过移动副连接，扭矩油缸7的两端分别通过球铰与鞍架6及水平支撑油缸10的缸筒连接，水平支撑油缸10通过球铰与撑靴8铰接，推进油缸11的两端分别通过球铰与主梁4和撑靴8连接，而鞍架6则通过由球铰及移动副组成的十字销轴5与水平支撑油缸10连接。

分析支撑-推进-换步机构中各弹性环节刚度拓扑关系可知，各驱动油缸油液相比系统中其余钢制构件均视为薄弱环节。为建立更加直观、实用且适用范围更广的机构动力学模型，在建模时最大限度的忽略次要因素和局部振动的影响，将整个机构视为一个集中参数，并把机构中所有驱动构件均视作弹性环节。基于上述分析与假设，定义系统广义坐标列阵

u＝[xcyczcθcxθcyθcz]^t

式中，xc、yc及zc分别代表机构质心沿水平、竖直及隧道掘进方向平移的位移坐标；θcx、θcy及θcz分别代表机构质心绕水平、竖直及隧道轴线扭转的位移坐标。

考虑液压驱动系统刚度、运动副刚度、阻尼及尺度参数等因素，建立机构处于一个掘进行程中任意位置的动力学模型，如图2所示。在图2中，od、ob及oc分别代表刀盘几何中心、护盾总几何中心及机构质心；of代表破岩载荷等效作用点；o1、o2代表两侧撑靴几何中心；o3、o4代表两侧推进油缸与主梁的铰接点；o5、o6代表两侧扭矩油缸与鞍架的铰接点；l1、l2、l3及l10分别代表oc与ob、o3(o4)、o1(o2)及od沿z轴距离；l4、l7分别代表oc与o3(o4)、o1(o2)沿x轴距离；l11、l13代表oc与od、o5(o6)沿x轴距离；l5、l6及l12分别代表oc与o3(o4)、o1(o2)及od沿y轴距离；l8、l9分别代表of与od沿y、x轴距离；r为刀盘半径；α、β分别代表推进油缸和扭矩油缸的倾斜角度；fdx(t)、fdy(t)、fdz(t)及tdz(t)分别代表滚刀破岩时沿x、y及z向等效力及绕z轴等效力矩；k1x、k2x、k3x、k4x和k1y、k2y、k3y、k4y分别代表各护盾与围岩支撑界面沿x、y向等效刚度；k6x和k6y分别代表撑靴与围岩支撑界面沿x、y向等效刚度；k5代表主梁一侧推进油缸总刚度；kn代表两侧扭矩油缸刚度；kzc代表支撑油缸刚度；ksx、ksy分别代表十字销轴沿x、y向等效刚度；kwx、kwy代表围岩沿x、y向等效刚度；c1x、c1y、c2x、c2y、c3x、c3y、c4x、c4y、c5x、c5y、cn、czc、csx、csy、cwx及cwy分别代表与上述弹性环节相对应的阻尼。

利用牛顿-欧拉法建立机构运动微分方程

式中，k6x和k6y代表撑靴-围岩支撑界面沿x、y方向的等效刚度，可表示为

将机构运动微分方程进一步整理为矩阵形式，得到

式中，u为广义坐标列阵，m为质量矩阵，k为刚度矩阵，c为瑞利阻尼矩阵，q(t)为广义激励力列阵。各矩阵的具体形式如下：

广义坐标列阵

u＝[xcyczcθcxθcyθcz]^t

质量矩阵

m＝diag(mcmcmcjcxjcyjcz)

刚度矩阵：

式中，kij(i,j＝1,2,3,4,5,6)分别代表刚度矩阵各位置元素：

k11＝k1x+k2x+k3x+k4x+2k5sin²α+2k6x；k12＝0；k13＝0；k14＝0

k15＝(k1x+k2x+k3x+k4x)l1-2k5sin²αl2-2k6xl3；k16＝-k2xr+k4xr+2k5sin²αl5+2k6xl6；

k21＝0；k22＝k1y+k2y+k3y+k4y+2k6y；k23＝0；k24＝-(k1y+k2y+k3y+k4y)l1+2k6yl3；k25＝0；

k26＝(k1y-k3y)r；k31＝0；k32＝0；k33＝2k5z；k34＝-2k5zl5；k35＝0；k36＝0；

k41＝0；k42＝-(k1y+k2y+k3y+k4y)l1+2k6yl3；k43＝-2k5cos²αl5；

k44＝(k1y+k2y+k3y+k4y)l1²+2k6yl3²+2k5cos²αl5²；k45＝0；k46＝0；

k51＝(k1x+k2x+k3x+k4x)l1-2k5sin²αl2-2k6xl3；k52＝0；k53＝0；k54＝0；

k55＝(k1x+k2x+k3x+k4x)l1²+2k5sin²αl2²+2k6xl3²+2k5zl4²；k56＝0；

k61＝(-k2x+k4x)r+2k5sin²αl5+2k6xl6；k62＝(k1y-k3y)r；k63＝0；k64＝0；k65＝0；

k66＝(k2x+k4x+k1y+k3y)r²+2k5sin²αl5²+2kncos²βl13²

瑞利阻尼矩阵：

式中，cij(i,j＝1,2,3,4,5,6)分别代表阻尼矩阵各位置元素；a和b均为比例阻尼系数，其取值可通过机构的基频和对振动能量贡献较大的频率值确定；

广义激励力列阵

q(t)＝[fxfyfztxtytz]^t

式中，

fx＝-fdx(t)；fy＝-fdy(t)；fz＝-fdz(t)；tx＝-[fdz(t)l8-fdy(t)l10]；

ty＝-[fdz(t)l9-fdx(t)l10]；tz＝-tdz(t)

根据机构运动微分方程，忽略其外部激励和内部阻尼，建立无阻尼线性自由振动方程

与之所对应的特征值问题为

式中，ωn、φn分别代表系统的第n阶固有频率和振型。

实施例1

以应用于辽宁大伙房输水工程的罗宾斯m264-311型tbm样机为例，其基本参数如表1所示；计算得到支撑-推进-换步机构处于初始掘进位置时的刚度、尺度及惯性参数如表2所示。

表1

表2

以表1、表2所给参数为例，根据特征值方程数值仿真分析机构前4阶固有频率及振型，结果分别如表3和图3所示。在图3中a代表振型矢量大小，l代表自由度(广义坐标)编号。

表3

从图3(a)、图3(b)、图3(c)和图3(d)中可见，机构前4阶振型分别主要表现为绕z轴扭转振动、沿x、z、y向平移振动。

以表1、表2中所给参数为例，并选取其中的扭矩油缸刚度参数kn为研究参数，研究其对机构固有频率的影响规律。具体做法为：

仅改变刚度参数kn，其它参数保持不变。根据特征值方程进行数值仿真，得到机构前4阶固有频率随刚度参数kn的变化曲线如图4所示。图中，点画线、点线、虚线和实线分别代表1～4阶固有频率变化曲线。

由图4可见，随着扭矩油缸刚度的增大，第1阶固有频率逐渐增大。表明通过调整扭矩油缸刚度参数的大小，可以增大第1阶固有频率，进而提高机构动态性能。因此，在tbm施工过程中，可以通过调整油液压力来实现增大扭矩油缸的刚度，进而实现提高tbm的工作效率和工作稳定性。研究结果为该类装备的结构参数优化设计提供了理论依据。

实施例2、

对本发明中建立的六自由度动力学简化模型的有效性分析

以上述tbm机型及表1、表2中所给参数为例，通过samcef建立支撑-推进-换步机构有限元模型并进行模态分析，得到前4阶固有频率及其模态振型分别如表4及从图5(a)、图5(b)、图5(c)和图5(d)所示。

表4

由图5(a)、图5(b)、图5(c)和图5(d)可见，机构前4阶振型分别为绕x轴扭转振动、沿z、x、y平移振动。

计算频率值相对误差如表5所示。

表5

由表5、图3(a)、图3(b)、图3(c)和图3(d)及图5(a)、图5(b)、图5(c)和图5(d)中可见，通过机构六自由度动力学简化模型仿真得到的前4阶固有频率及振型，与有限元模型仿真结果比较吻合，证明了本发明建模方法的有效性。

综上所述，本发明提供了一种用于开敞式tbm结构优化设计方法。该技术方案在满足能够准确描述机构基本动态特性的前提之下，基于机构组成及各构件间的刚度拓扑关系最大程度地忽略了次要因素的影响，不仅使模型的求解效率大大提高，还进一步提高了模型的直观性和实用性。除此之外，该模型的适用范围得到了拓宽。因此，本发明方法能够更好地满足工程实际的需求。

本领域技术人员可以理解附图只是一个特殊实施例的示意图，并不用以限制本发明。显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换和变型等，均应包含在本发明的保护范围之内。