一种风电场可用惯量评估方法与流程

本发明属于风电评估技术领域，尤其涉及一种风电场可用惯量评估方法。

背景技术：

本部分的陈述仅仅是提供了与本公开相关的背景技术信息，不必然构成在先技术。

风力发电因其清洁、高效和可再生等特点而成为了目前最具开发价值的新能源发电形式之一，但是随着风电在电网中渗透率不断提高，大量火电机组被风电所替代，整个电力系统的可用转动惯量持续减少，频率响应能力降低。在日益减少的火电机组逐渐难以独立承担不断增加的调频压力情况下，电网一定程度要求风电机组具备参与系统频率调整的能力。这种能力包含惯性响应、一次调频以及二次调频等多种时间尺度的频率响应方式。

发明人在研究中发现，目前国内外学者对于风电机组参与惯性响应的研究多集中于优化风机调频控制策略方面。文献“morrenj,haanswhd,klingwl,etal.windturbinesemulatinginertiaandsupportingprimaryfrequencycontrol[j].ieeetransactionsonpowersystems,2006,21(1):433-434.”提出了风机的虚拟惯量的概念，通过虚拟惯量控制风电机组可以吸收或释放转子动能来响应电网的频率波动。当风机通过降低转速释放旋转动能参与调频后，发电机转子需要吸收电网有功恢复转速，电网会出现频率的二次跌落现象。

针对该现象，文献“陈宇航，王刚，侍乔明，付立军，蒋文韬，黄河.一种新型风电场虚拟惯量协同控制策略[j].电力系统自动化，2015，39(05):27-33.”引入了风机转子动能评估因子的概念，根据该参数协调各台风机参与频率响应的方式，从而达到抑制频率二次跌落的目的。

文献“丁磊，尹善耀，王同晓，姜吉平，程法民，司君诚.结合超速备用和模拟惯性的双馈风机频率控制策略[j].电网技术，2015，39(09):2385-2391.”则是提出通过超速备用控制使风机越过mppt点运行，风机转子转速预留了可观的减速裕度，通过将减载控制和虚拟惯量控制相结合，最大化风电机组调频能力，同时可以有效解决转子转速恢复过程中造成的频率二次跌落问题。

相较而言，现有研究中针对风电机组或风电场参与电网调频服务能力的评估分析相对较少。文献“wul,infieldd.powersystemfrequencymanagementchallenges-aprobabilisticapproachtoassessingwindfarmpotentialforaidingsystemfrequencystability[c]//renewablepowergenerationconference.iet,2013.”及“wul,infieldd.towardsanassessmentofpowersystemfrequencysupportfromwindplant-modelingaggregateinertialresponse[j].ieeetransactionsonpowersystems,2013,28(3):2283-2291.”中提出一种基于虚拟惯量控制原理下的风机惯性能力的评估方法，通过对大气湍流的高斯概率分布模型进行分块处理来评估出特定平均风速下的风电场联合惯性响应能力。

在此研究基础上，“wul,infieldd.aprobabilisticapproachtoassessingcombineddroopandinertialresponsefromwindplant[c]//renewablepowergenerationconference.iet,2014.”中综合评估了惯性响应过程中的虚拟惯量控制以及下垂控制的联合调频效果，结果显示两种控制方式的协调运行可提高风电场有功功率的输出能力，提升风场调频性能。

此外，文献“leej,muljadie,sorensenp,etal.releasablekineticenergy-basedinertialcontrolofadfigwindpowerplant[j].ieeetransactionsonsustainableenergy,2015:1-10.”中的策略是通过评估风力发电机组可用惯性动能(kineticenergy，ke)来调整风机控制系统中虚拟惯量控制回路和下垂控制回路的增益。

由此可见，上述研究中均提出了确定惯性控制策略下的风场可用惯量评估方法。然而，所提方法中忽略了尾流效应、风剪切效应等环境因素影响，未考虑风场内各风机风速的时空分布特性，以及惯性响应过程中的大气湍流作用下的风速波动特性。同时，各算法中并未计及实时运行中风机处于故障停机状态对风机可用惯量的影响，所得评估结果与实际可用惯量值间的差值较大。因而，有必要构建考虑风场内各风机风速状况和运行工况下可用惯量评估方法。

技术实现要素：

为克服上述现有技术的不足，本发明提供了一种风电场可用惯量评估方法，为一种考虑风机风速分布和机组运行工况的可用惯量的概率化评估算法，能够减小算法评估结果与实际值的误差，为电力系统运行调度提供高可信度的风场可用惯量的评估结果。

为实现上述目的，本发明的一个或多个实施例提供了如下技术方案：

一种风电场可用惯量评估方法，包括：

基于物理因素影响下风场平均风速的时空分布特性，并利用混合copula函数，构建大气湍流影响下的瞬时风速条件概率分布模型；

以双馈风电机组虚拟惯量控制下的运行方式建立风机可用惯性动能和惯性功率增量的估算模型，并额外考虑实际运行中风场各风机的运行工况，得到基于一定置信度下全风场的可用惯量的区间评估曲线。

进一步的技术方案，通过对尾流效应、风剪切效应和时延效应三类物理影响因素进行分析获得风能在风场的位置分布和时间变化特性，进而利用copula函数在相关性分析中的优势，构建大气湍流影响下的短时风速条件概率分布模型。

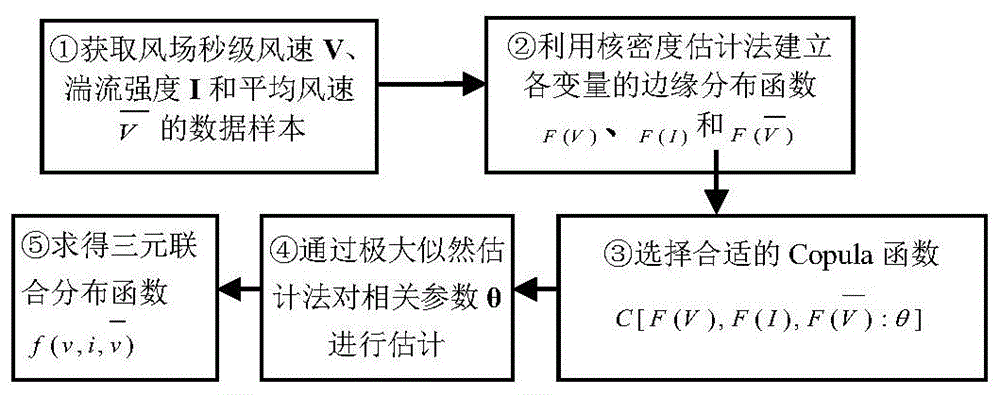
进一步的技术方案，获取风场秒级风速、湍流强度和平均风速的数据样本，利用核密度估计法建立各变量的边缘分布函数，选择合适的copula函数，通过极大似然估计法对相关参数进行估计，求得三元联合分布函数。

进一步的技术方案，全风况下按风电机组捕获有功功率和转子转速情况可分为启动区、最大功率跟踪区、恒转速区、恒功率区和切出风速区。

进一步的技术方案，将风机的可用惯量从能量和功率两个方面分为存储在风机上的可用惯性动能和惯性响应中惯性动能提供的可用惯性功率增量。

进一步的技术方案，可用惯量评估算法按风机故障情况和所处风速分区情况将风场内的单台风机的可用惯量可分为三种状态，分别为无可用惯量、恒定可用惯量和变化可用惯量；

无可用惯量和恒定可用惯量状态均以单个概率值表示，变化可用惯量状态通过连续的概率密度函数表示风机可用变量的分布情况。

进一步的技术方案，评估方法中，假定风场内各风机间仅存在尾流效应影响下的风速联系，对于风速分布已知情况下，在算法的区间估计时各风机可用惯量按独立随机变量处理。

进一步的技术方案，全风场的可用惯量置信区间的获取步骤如下：

step1:按风机的可用惯量评估方法分别获得风电场实时运行时每台风电机组可用惯量的概率密度函数f(e)和f(p)；

step2:对f(e)和f(p)积分获得可用惯量的概率分布函数φ(e)和φ(p)；

step3:采用二分查找-数值积分法求取可用惯量分布函数在和概率值处风机j对应的惯量值，即分别获得各风机j在置信度α下的可用惯量的置信区间；

step4:风场各风机可用惯量叠加求得全风场的可用惯量的置信区间。

本发明公开了一种风电场可用惯量评估系统，包括：

分布模型建立模块，基于物理因素影响下风场平均风速的时空分布特性，并利用混合copula函数，构建大气湍流影响下的瞬时风速条件概率分布模型；

求解模块，以双馈风电机组虚拟惯量控制下的运行方式建立风机可用惯性动能和惯性功率增量的估算模型，并额外考虑实际运行中风场各风机的运行工况，得到基于一定置信度下全风场的可用惯量的区间评估曲线。

以上一个或多个技术方案存在以下有益效果：

针对风电场参与调频服务时，惯性响应能力缺乏准确估计的问题，提出了一种考虑风场风速分布和风机运行工况的风场可用惯量概率化评估方法。分别从能量和功率两个方面，获得基于一定置信水平下的风场可用惯性动能和可用惯性功率增量的评估曲线。

本申请所提的置信区间评估结果误差较小，具有较高的可信度。

附图说明

构成本发明的一部分的说明书附图用来提供对本发明的进一步理解，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。

图1为本发明实施例两机尾流线性扩张示意图；

图2为本发明实施例风场风速联合分布函数构建流程图；

图3为本发明实施例全风况下dfig机组运行状况示意图；

图4为本发明实施例风电场风机布置示意图；

图5为本发明实施例90％置信度下风场可用惯量-风速曲线图；

图6为本发明实施例置信度为90％时风电场可用惯性动能置信区间图；

图7为本发明实施例置信度为90％时风电场可用惯性功率增量置信区间图；

图8为本发明实施例不同置信水平下风电场可用惯量评估曲线图；

图9为本发明实施例仿真结果统计图。

具体实施方式

应该指出，以下详细说明都是示例性的，旨在对本发明提供进一步的说明。除非另有指明，本文使用的所有技术和科学术语具有与本发明所属技术领域的普通技术人员通常理解的相同含义。

需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本发明的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。

在不冲突的情况下，本发明中的实施例及实施例中的特征可以相互组合。

本发明提出的总体思路：

风电场内风机一般采用确定的惯性响应策略，但由于受尾流、湍流等复杂环境因素影响，场内各风电机组的风速时空分布以及实时运行状况具有单机间的差异性，风场可用惯量值与标称值可能存在较大误差。为此，提出了一种考虑风机风速分布和机组运行工况的可用惯量的概率化评估算法。通过研究物理因素影响下风场平均风速的时空分布特性，并利用混合copula函数，构建大气湍流影响下的瞬时风速条件概率分布模型。以双馈风电机组(dfig)虚拟惯量控制下的运行方式建立风机可用惯性动能和惯性功率增量的估算模型，并额外考虑实际运行中风场各风机的运行工况，得到基于一定置信度下全风场的可用惯量的区间评估曲线。以实际风电场的结构及运行数据为例进行单个风场的可用惯量评估，通过simulink仿真平台搭建风场模型，利用统计数据验证置信区间评估结果的有效性。

实施例一

本实施例公开了一种风电场可用惯量评估方法，采用风电场测风塔测得的精度较高的风速信息，通过空气传播原理和混合copula函数构建风电场瞬时风速的概率分布模型。在此基础上，分析虚拟惯量控制在电网频率响应中的惯量释放情况，进一步从能量和功率两个方面给出了风电机组实时可用惯量的概率化评估方法。

首先介绍基于混合copula函数的风场风速建模，风场风速分布是影响风机运行情况的重要因素。因而，通过对尾流效应、风剪切效应和时延效应三类物理影响因素进行分析可以获得风能在风场的位置分布和时间变化特性。进而利用copula函数在相关性分析中的优势，构建大气湍流影响下的短时风速条件概率分布模型。

关于jensen尾流模型，尾流效应描述的是自然风从上游风机吹向下游风机时出现的风速递减的现象。目前，针对尾流效应模拟提出了许多模型，其中使用最为广泛的是jensen尾流模型，其计算基础为风机尾流扩张理论，即在不考虑湍流影响下，可近似认为尾流的影响随着距离呈线性扩张趋势，自然风经风机风轮后呈圆锥形扩散，且沿截面均匀分布。两机线性扩张示意图如图1所示。

综合考虑风场各风机对风机j的尾流效应，有

式中：v0表示上游机组自然风速；b(j,k)表示风机k对风机j的尾流影响系数，由机组k对机组j的遮挡面积ajk和机组j的扫风面积aj的比值决定；vwk为机组k尾流后的风速。

关于风剪切效应，风剪切效应指的是风速随垂直高度增加而增加的现象，对于山地风电场等复杂地形的风电机组，风剪切效应对轮毂高度处的风速的影响十分显著。考虑风剪切效应下的风速计算通常使用指数模型：

式中：v(z)为z高度处的风速；vh表示轮毂高度处风速；α为风剪切系数。

关于时延效应，风电场实时风况从上风向机组传递到下风向机组存在明显的时间延迟，并且在考虑尾流作用的情况下，风速受尾流影响下的时间延迟现象更加明显。当风速从风电场站场端到风机j的延迟时间为τ时，结合式(1),时延效应下风机j处的风速为

关于copula函数，通过分析风电场尾流效应、剪切效应和时延效应建立的风速模型能够较好的描述风场分钟级的平均风速的时空分布状况，但是对于秒级的频率响应，该风速模型不够精确。copula函数是一类描述多变量相依关系的连接函数，起初主要用于概率度量空间理论，后经改善被用于确定随机变量间的非参数估计中。利用copula连接函数的特点可进一步精确化描述考虑大气湍流影响下的瞬时风速的概率分布状况。sklar定理指出，存在一个copula概率分布函数c，对任意的x∈rⁿ有：

f(x1,x2,...,xn)＝c[f1(x1),f(x2),...,f(xn)](5)

式中：fi(xi)为随机变量xi的边缘密度函数；c为copula概率密度函数，令ui＝fi(xi)，则c可表示为

混合copula函数的相关结构比单个copula函数更加灵活，可以反映不同随机变量间的相关模式。现有文献提出了两元混合copula函数的概念，类似地，可以得到多元混合copula函数为

式中：ω1，ω2，ω3为各copula函数的权重系数，满足ω1+ω2+ω3＝1；α、β和γ为各copula函数的相关系数。

关于风速概率分布模型，风场风速建模的相关研究中已有文献对秒级瞬时风速的精确刻画。现有技术存在通过仿真模拟出考虑湍流、白噪声等多种影响因素的瞬时风速波形。在此基础上，考虑到实时运行时风场风速受大气湍流作用具有较大的波动性，即认为风机轮毂高度处风速在惯性响应中是变化的。因而，本申请提出利用混合copula函数建立综合考虑瞬时风速、大气湍流强度以及平均风速影响的三元联合分布函数，构建流程如图2所示。

核密度估计法(kerneldensityestimation，kde)是目前应用较为广泛的非参数估计方法之一，kde中不同核函数对于非参数估计结果影响较小步骤2中,通过kde可构建的概率密度函数

式中：n为样本数；h表示窗宽；k(·)表示核函数；xi为数据样本点i。同时本文采用高斯核函数k(δ)。

通过对风电场的风速和气象数据进行kde处理，可得到瞬时风速v、平均风速和湍流强度i的边缘密度函数f(v)、f(i)和再通过对密度函数积分获得所需边缘分布函数f(v)、f(i)和

阿基米德函数族中，clayton-copula、gumbel-copula和frank-copula分别适合描述下尾部、上尾部和对称数据的相依关系。因而，步骤3和4综合三种copula函数的优点，建立风场风速的三元混合copula函数为

式中：θ1，θ2，θ3分别三类copula函数关于v,i和三个随机变量的相关系数。

最后，步骤5是通过式(6)、(7)和(11)可以获得描述风电场瞬时风况的三元联合密度函数

构建风电场瞬时风速、湍流强度和平均飞速的三元分布函数直接目的是为式(13)的瞬时风速条件概率分布模型建立做基础，以此建立适合描述惯性响应过程的秒级精细风速状况的模型，从而更为准确的评估出风场的惯量状况。

后续多元分布模型主要是代入式(13)中的以及相同方法获得的中。

惯性响应时，对于实时运行的风电机组，认为已知平均风速和湍流强度条件下，瞬时风速的条件概率分布情况是确定的。由此可以给出基于特定平均风速和湍流强度下的瞬时风速的概率密度函数

式中：表示条件分布函数，推导过程如式(14)所示。其中，通过上述提出的联合密度函数构建流程求得。

基于特定平均风速和湍流强度下的瞬时风速的概率密度函数能够更为精确的描述的实时运行中风场瞬时风速的概率分布情况，从而由风速的分布建立单机以及全风场的可用惯量的概率分布模型。即式(26)和(27)的和两式。

可用惯量评估方法：虚拟惯量控制：随着双馈风电机组风轮重量不断增加，正常运行时风轮、转子等结构中存储的总惯性动能变的十分巨大。充分挖掘风机的转动惯量能够极大降低电网频率事故时的频率波动的最低点(最高点)，提高频率恢复速度。目前，通过电力电子设备对风电机组施加惯性控制环节可以使得风力发电机组在面临频率事故时能像同步机一样释放或存储风机转动部分的旋转动能，这种控制方式被称为虚拟惯量控制。不考虑风机主动减载运行情况下，当dfig采用虚拟惯性控制时，风机存储的惯性动能为

式中：ω为风机正常运行时的转子转速；j为包含发电机转子、风轮等多种转动结构的总转动惯量。

从功率角度出发，对存储在双馈风电机组旋转转子以及相关耦合旋转部件中的惯性动能求导可获得风机实时可提供的惯性功率支撑

式中：ωn为风机的额定转速；f为电网频率。

全风况下风机转子转速：双馈发电机组运行状况示意图3所示，全风况下按风电机组捕获有功功率和转子转速情况可分为启动区、最大功率跟踪区(mppt)、恒转速区、恒功率区和切出风速区。

对不同的分区按风速段计算相应概率值，见式(30)。

得到的各风速区的概率值主要用在式(28)、(29)和(31)中，通过风速分区来进行风场可用惯量的分类，进而描述整个风场的可用惯概率分布情况。

i&v启动区和切出风速以上：此时受风速状况限制，风机无法正常并网运行。因而，该风速区内，风电机组不参与电力系统频率响应，无可用惯量。

ii最大功率跟踪区：如图3所示，在中低风速下，通过风机mppt控制可以使得风机正常运行时，输出功率在输出曲线的最高点。风机捕获的机械功率pm如下式所示

式中：ρ为空气密度；cp为风能转换效率；λ为叶尖速比，定义为λ＝ωtr/v，其中：ωt为风机叶轮旋转角速度；β为桨距角；a为风机扫风面积。

风机工作在ii区时，风能转换效率cp最大，此时，桨距角β＝0，同时，风机运行满足式(18)

λ＝λopt(19)

通过上式求得最优叶尖速比λopt，由叶尖速比的定义可以得到线性化的风机转速-风速关系式

式中：ω为风力发电机转子转速；g为风机齿轮箱传递系数。

iii恒转速区:处于恒转速区的风机的转速随风速增加变化较小，但此时风机的捕获功率仍呈现上升趋势。根据现有文献所提出的风机功率曲线关系可推得近似线性化的转子转速的方程，其中各参量与图3对应。

iv恒功率区:当风机轮毂处的风速超过额定风速后，风机输出功率将不会继续增加，此时风力发电机转子转速和输出功率均恒定不变，且转子转速处于最高转速。

ω＝ωmax(22)

可用惯量评估方法，风电场内风机实时并网运行时，影响风场内风机可用惯量的因素主要归结为风场风况和各风机的运行工况两个方面。通过物理模型对风在场站内的传播进行分析，采用概率分布的形式描述各风机风速在惯性响应过程中的瞬时波动特性。本节中将在单个风机可用惯量评估算法中引入风机运行工况，主要考虑运行过程中风场机组故障情况以及风机惯性控制策略的状况。同时，本申请分析中将风机的可用惯量从能量和功率两个方面分为存储在风机上的可用惯性动能和惯性响应中惯性动能提供的可用惯性功率增量。

正常运行情况下(无减载控制)，风机转速随风速状况变化处于不同的区域，在考虑尾流影响下，风场内不同转速区风机的可用惯量因风速状况不同存在较大的差异。因而，从单台风机的可用惯量出发，进而评估全风场的可用惯量的方式能显著提高估算精度。对于单台双馈风电机组，其转动机构中存储的旋转动能在惯性响应过程中是无法全部释放，这是因为当风力发电机转子转速降低到最低允许转速ωmin(通常为0.7p.u)时，风机将会退出运行。因而，风场内某风机j的可用转子惯性动能为

由图3可以看出，全风速下各风机运行状况具有较大的差异。风机并网运行后，在中低风速状态下的双馈风机能保持mppt状态(区域ii)运行，但需保证ej>0，即风机轮毂处实际风速时(区域ii2)，风机才开始具有惯性响应能力。当达到额定风速后，风机j的转子转速保持恒定不变，可用惯量为确定值。最后，处于切出风速区的风机无法正常运行，风机失去惯性响应的能力，即无可用惯量。综上所述，全风况下风机j的可用惯性动能按风速状况可分为下式所示的四个阶段。

类似的，结合式(16)和(20-22)，从功率角度考虑，虚拟惯性控制下的风机j在全风速状况下的可用惯性功率增量可以表示为

此处得到的单台风机j的可用动能和功率支撑分布模型g(v)和h(v)将用于式(28)和(31)中，即反函数g^-1(ej)和h^-1(pj)。

上述分析中给出了风机j可用惯量-风速的两个关系式g(v)和h(v)，可以看出，不考虑机组运行状态时，单个风机的可用惯量可由风速决定。同时，风机j在惯性响应内的风速可由函数分布描述。因而，结合随机变量反函数概率密度理论可以得到实时运行中特定平均风速和特定湍流强度下风机j的可用惯性动能和可用惯性功率增量的概率密度函数模型

此外，单台风机装机容量的不断增加的情况下，实时评估过程中对于风机运行状态已经无法忽视，因为单台大容量风电机组的故障直接会使得整个风场惯性输出能力突降。假设由风机统计数据得到风机j的故障率为pj时，单机j的可用惯量的概率密度函数分别为

pξ＝pi+pii1+piv+pv(29)

式中：pi,pii1,piv,pv表示风机运行在图3所示对应风速区域i,ii1,iv和v的概率值。对于任意风速区x，px的表达式为

可以看出，所提可用惯量评估算法按风机故障情况和所处风速分区情况将风场内的单台风机的可用惯量可分为三种状态，分别为无可用惯量、恒定可用惯量和变化可用惯量。无可用惯量和恒定可用惯量状态均以单个概率值表示，变化可用惯量状态通过连续的概率密度函数表示风机可用变量的分布情况。相应的，从功率释放角度出发，可用惯量的分布情况为

评估方法中对上述风速模型主要处理有两点：1)应用于式(30)来获得各风速分区对应概率值。2)应用于式(28)和(31)中的和来描述ej和pj处的概率密度值。

整个评估模型的处理中，首先是通过分析风机虚拟惯性控制策略情况获得各分区状况下单台风机可用惯量，即式(24)和(25)。进而以此为基础建立考虑风机故障概率以及风速概率分布情况下的单台风机可用惯量分布,(28)和(31)。最后利用叠加求和的方式获得全风场可用惯量的置信区间结果，即式(32)-(35。

可用惯量置信区间：相对于确定性的评估结果，以一定置信度下的置信区间的形式给出的风电场可用惯量评估结果对系统调度更有参考性和指导性。本文的评估算法里，假定风场内各风机间仅存在尾流效应影响下的风速联系，对于风速分布已知情况下，在算法的区间估计时各风机可用惯量按独立随机变量处理。因而，全风场的可用惯量置信区间的获取步骤如下：

step1:按上文所提的风机j的可用惯量评估方法分别获得风电场实时运行时每台风电机组可用惯量的概率密度函数f(e)和f(p)。

step2:对f(e)和f(p)积分获得可用惯量的概率分布函数φ(e)和φ(p)

step3:采用二分查找-数值积分法求取可用惯量分布函数在和概率值处风机j对应的惯量值，即分别获得各风机j在置信度α下的可用惯量的置信区间

ωej＝[ejd,eju](32)

ωpj＝[pjd,pju](33)

step4:风场各风机可用惯量叠加求得全风场的可用惯量的置信区间为

算例及仿真：以西北某实际风电场(简称风场a)为例，采用的风场实测的风速数据进行单个风场可用惯量的评估。风电场a有6排共108台双馈异步风电机组，风电场场站内风机布置示意图如图4所示。

评估算法对比分析：

以风电场a结构布局进行全风速风场可用惯量的评估，设定整个评估算例以负荷突增情况下，电力系统频率跌落为场景，分析风场实时可释放的惯性动能情况。

风场a盛行风向为西，即θ＝90°。取可用惯量评估的置信度水平为0.9，当风场接收到电网频率跌落信号，控制系统控制风机参与惯性响应，通过评估算法得到不同风电场场端风速下的全风场的可用惯量区间评估结果如图5所示。算例中标称值曲线是通过忽略风场内各机组差异，采用单机等值化处理得到的风场可用惯量评估结果。

从图5可以看出，风速小于切出风速情况时，风电场存储的旋转动能整体随场端风速增加呈上升趋势。启动风速后的小部分风速区，风场仍不具备惯性响应能力，这主要是因为该风速区中风场a内的各风机转子转速均低于最低转速ωmin，转速无下调裕度，因而风场仍无法向电力系统提供惯性响应支撑。

当处于中高风速区时，风场开始具备参与惯性响应的能力，此时风场的可用惯量随风速升高快速增加，相应的置信区间也在不断扩大，并且由于忽略各风机的运行差异，标称算法结果始终高于所提算法的评估结果。对于部分达到额定风速后运行的机组，发电机转速不在增加，惯性动能保持恒定，但全风场总的可用惯量由于尾流存在仍呈现上升趋势。此时，由图5曲线可知，标称算法中所有机组均被视为恒转速运行状态，风场可用惯量处于恒定不变的状态，所得评估结果偏高。

当风场场端风速超出切出风速(25m/s)时，部分前排风电机组将退出运行，出现风场总的可用惯量的骤降现象,而标称算法中所有机组均与电网解列，评估曲线骤降到0值。两种算法相比，所提方法可有效减少估算结果与实际值之间的误差，同时置信区间形式的评估曲线可提供该电网运行调度更为直观可信的参考结果。

实时运行，以风电场a夏季某日上午6时至12时实测风速数据进行可用惯量评估。评估算法综合考虑了尾流效应、时延效应、风剪切效应以及大气湍流等各类影响因素。从惯性响应的能量角度分析，整个风电场可用惯量变化曲线图6所示。

所取的上午6时至12时的时间窗口内，风场场端风速保持在9.5-14m/s之间变化，大部分风机运行在图3所示的区域ii(mppt)和区域iii(恒转速区)。结合图6评估曲线可知，整个可用惯量评估曲线基本呈现出跟随实时风速变化趋势同步改变的现象，能够为电力系统调度提供直观的风场可用惯量的时变情况。对于任意时刻，0.9置信度下的风场可用惯量真值可视为在置信下界和置信上界间。

另一方面，从风电场内双馈风机惯性响应过程中的有功功率释放角度出发，实时的风场可用惯量评估曲线为图7所示。

由图6和图7可知，风场风机存储的旋转动能和短时可增发的有功功率实时评估曲线基本一致，均能实时地显示风场可用惯量的变化趋势。两类阶梯状的评估曲线均出现了可用惯量数值陡升或陡降现象，这类现象主要是由于所提实时评估算法在计算存在着时间间隔，相邻时间间隔内的风速变化越大，风场的可用惯量结果变化也更剧烈。

多种置信度水平下的评估结果能够突出风场可用惯量的裕度大小。选取不同置信度水平下，可以得到风场可用惯量曲线为图8所示。

如图8所示，黑线所示的不考虑湍流条件的评估曲线。可以看出，考虑大气湍流下各置信度下的可用惯性动能的评估与无湍流下的曲线保持同步变化趋势。随着置信度的提高，可用惯量的置信区间不断增大，即区间评估的风险减少，但相应的算法的输出评估结果波动范围变大。因此，当系统决策者制定调度计划时，可根据实时电网的运行情况以及各风电场的不同置信度下的可用惯量评估曲线来制定基于特定风险性下的最优调频方案，同时也可根据可用惯量评估曲线变化情况对风电场实时惯性响应调频策略进行针对性的调整。

置信区间评估方式有效性验证：上述算例结果证明了所提算法能有效减小可用惯量评估结果与实际值间的误差，但并未对所得置信区间评估结果的有效性进行验证。现阶段，风机的惯性响应能力可以视为风机“隐藏”的一种能力，通常仅在接收到电网频率事故信号时才会显现出来。目前的研究难以直接获取大量风场实时运行时惯性响应状况的数据信息。因而，本文通过在simulink平台搭建等效的6排双馈异步风电机组的风场模型，对每台风电机组施加多组按分布的风速模拟实际风场的实时风速状况，并对每台风机均施加虚拟惯量控制环节，设定系统在特定时间发生频率事故，记录各类风况下的功率输出曲线，并获得风机旋转动能释放情况，最后通过统计大量仿真结果来验证区间评估结果的有效性。

通过对320组仿真结果进行统计，统计结果如图9所示。当不考虑湍流影响时，通过不同的系统中风机联合转动惯量j算例估计，使得所提算法所得结果与统计结果相比,得到风机可用惯性动能保持较少误差水平，从而估算出仿真系统风机的转动惯量j。当考虑湍流影响时，通过所提区间评估方法进评估，算法结果与实际统计数据相比，超出置信区间的误差比例如表1所示。可以看出，所提方法在置信度较高时误差较小，各置信度下误差均为超出风险上限，因而所提算法能较好地评估出风场实时运行中的惯性响应状态与能力。

表1不同置信度水平评估结果误差

本申请针对风电场参与调频服务时，惯性响应能力缺乏准确估计的问题，提出了一种考虑风场风速分布和风机运行工况的风场可用惯量概率化评估方法。分别从能量和功率两个方面，获得基于一定置信水平下的风场可用惯性动能和可用惯性功率增量的评估曲线。以西北某实际风场的结构和风速数据对本文所提的评估算法进行算例分析。结果表明，本文所提的方法具有较强的参考性和指导性。同时，利用simulink搭建等效风场模型进行仿真验证，由大量的统计结果可以看出本文所提的置信区间评估结果误差较小，具有较高的可信度。此外，随着后续参与惯性响应等调频服务的风场数量的提高，可进一步通过实际风场惯性响应数据验证所提方法的有效性。

实施例二

本发明公开了一种风电场可用惯量评估系统，包括：

分布模型建立模块，基于物理因素影响下风场平均风速的时空分布特性，并利用混合copula函数，构建大气湍流影响下的瞬时风速条件概率分布模型；

求解模块，以双馈风电机组虚拟惯量控制下的运行方式建立风机可用惯性动能和惯性功率增量的估算模型，并额外考虑实际运行中风场各风机的运行工况，得到基于一定置信度下全风场的可用惯量的区间评估曲线。

实施例三

本实施例的目的是提供一种计算装置,包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述程序时实现以下步骤，包括：

基于物理因素影响下风场平均风速的时空分布特性，并利用混合copula函数，构建大气湍流影响下的瞬时风速条件概率分布模型；

以双馈风电机组虚拟惯量控制下的运行方式建立风机可用惯性动能和惯性功率增量的估算模型，并额外考虑实际运行中风场各风机的运行工况，得到基于一定置信度下全风场的可用惯量的区间评估曲线。

实施例四

本实施例的目的是提供一种计算机可读存储介质。

一种计算机可读存储介质，其上存储有计算机程序，该程序被处理器执行时执行以下步骤：

基于物理因素影响下风场平均风速的时空分布特性，并利用混合copula函数，构建大气湍流影响下的瞬时风速条件概率分布模型；

以双馈风电机组虚拟惯量控制下的运行方式建立风机可用惯性动能和惯性功率增量的估算模型，并额外考虑实际运行中风场各风机的运行工况，得到基于一定置信度下全风场的可用惯量的区间评估曲线。

以上实施例二、三和四的装置中涉及的各步骤与方法实施例一相对应，具体实施方式可参见实施例一的相关说明部分。术语“计算机可读存储介质”应该理解为包括一个或多个指令集的单个介质或多个介质；还应当被理解为包括任何介质，所述任何介质能够存储、编码或承载用于由处理器执行的指令集并使处理器执行本发明中的任一方法。

本领域技术人员应该明白，上述本发明的各模块或各步骤可以用通用的计算机装置来实现，可选地，它们可以用计算装置可执行的程序代码来实现，从而，可以将它们存储在存储装置中由计算装置来执行，或者将它们分别制作成各个集成电路模块，或者将它们中的多个模块或步骤制作成单个集成电路模块来实现。本发明不限制于任何特定的硬件和软件的结合。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。

上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。