一种欺骗路径生成方法及装置与流程

本发明涉及路径规划技术领域，特别是指一种欺骗路径生成方法及装置。

背景技术：

一些场景中，通常会提供一些虚假信息来迷惑对方。比如，一方需要从位置a移动至位置b，但不希望另一方获取到自己的真实路径，该方可以设定虚假位置c，并在位置a、b、c之间规划欺骗路径，以隐瞒自己的真实路径。

现有方案中，大多是由相关人员设定欺骗路径，而由于环境因素及其他各种因素的复杂性，需要相关人员具备丰富的经验才能制定出合适的欺骗路径。合适的欺骗路径可以理解为消耗对方较多时间或者其他资源的路径，或者也可以理解为让对方较难确定出真实路径的路径。

可见，现有方案过多依赖人工经验，因此目前亟需一种自动规划出欺骗路径的方案。

技术实现要素：

有鉴于此，本发明的目的在于提出一种欺骗路径生成方法及装置。

基于上述目的，本发明提供了一种欺骗路径生成方法，包括：

确定起始节点、真实目标节点、预设虚假目标节点和多个中间节点；

基于最短路径规划模型和识别方行为模型，获取给定观测情形下的候选节点集合在每个中间节点位置处的后验概率分布，所述候选节点集合包括所述真实目标节点和预设虚假目标节点；

基于所述后验概率分布，评估中间节点的欺骗量级；

根据中间节点的欺骗量级，求解预设目标函数下的候选子路径；

将所述候选子路径组合成欺骗路径，所述欺骗路径以所述起始节点为起始点。

可选的，所述基于最短路径规划模型和识别方行为模型，获取给定观测情形下的候选节点集合在每个中间节点位置处的后验概率分布，所述候选节点集合包括所述真实目标节点和预设虚假目标节点，包括：

利用如下算式，计算所述后验概率分布：

y＝costdifms(s，g，n)；

其中，p(g|n)表示所述后验概率分布，n包括所述起始节点s、所述候选节点集合g和中间节点，α表示归一化因子，β表示一个预设常数，β大于0，costdifms表示意图的代价差，g表示所述真实目标节点和所述预设虚假目标节点，n表示最近观测到被识别方的位置，n＝o^|o|，o表示给定观测情形对应的观测序列。

可选的，所述基于所述后验概率分布，评估中间节点的欺骗量级，包括：

基于示伪策略和/或藏真策略、以及所述后验概率分布，评估中间节点的欺骗量级。

可选的，基于示伪策略以及所述后验概率分布，评估中间节点的欺骗量级，包括：

利用如下算式，评估中间节点的欺骗量级：

基于藏真策略以及所述后验概率分布，评估中间节点的欺骗量级，包括：

利用如下算式，评估中间节点的欺骗量级：

基于示伪策略和藏真策略、以及所述后验概率分布，评估中间节点的欺骗量级包括：

combi(o·n)＝ω1·simulation(o·n)+ω2·dissimulation(o·n).

其中，o表示给定观测情形对应的观测序列，n表示最近观测到被识别方的位置，n＝o^|o|，gr表示所述真实目标节点，p(gi|o.n)表示所述后验概率分布，g表示所述候选节点集合，simulation表示基于示伪策略得到的欺骗量级，dissimulation表示基于藏真策略得到的欺骗量级，ω1表示预设第一权重值，ω2表示预设第二权重值，combi表示基于示伪策略和藏真策略得到的欺骗量级。

可选的，所述预设目标函数为：以欺骗量级最大为目标的函数；所述根据中间节点的欺骗量级，求解预设目标函数下的候选子路径，包括：

利用如下算式，求解候选子路径：

目标函数为：

约束条件为：

x＝{x∈{0，1}^|e||r^tx≤r}

其中，k表示节点之间的边，若边k被通行，则xk＝1，否则xk＝0，magk表示边k上的欺骗量级值，-∞<magk<+∞；k∈fs(i)表示节点i的出边集合，k∈rs(i)表示节点i的出边集合，n表示所有节点的集合，s表示所述起始节点，gr表示所述真实目标节点，r表示s-gr路径的可用资源总量，e表示所有k组成的集合。

可选的，所述预设目标函数为：以欺骗量级最大以及路径最长为目标的函数；所述根据中间节点的欺骗量级，求解预设目标函数下的候选子路径，包括：

利用如下算式，求解候选子路径：

目标函数为：

约束条件为：

x＝{x∈{0，1}^|e||r^tx≤r}

其中，k表示节点之间的边，若边k被通行，则xk＝1，否则xk＝0，magk表示边k上的欺骗量级值，-∞<magk<+∞,rk大于0，rk表示通行边k所需要的资源；k∈fs(i)表示节点i的出边集合，k∈rs(i)表示节点i的出边集合，n表示所有节点的集合，s表示所述起始节点，gr表示所述真实目标节点，r表示s-gr路径的可用资源总量，e表示所有k组成的集合。

可选的，所述将所述候选子路径组合成欺骗路径，所述欺骗路径以所述起始节点为起始点，包括：

基于预设环路条件，识别所述候选子路径组合成的环路；

基于所述起始节点、所述真实目标节点、以及识别出的环路，生成由候选子路径组成的欺骗路径。

基于上述目的，本发明还提供了一种欺骗路径生成装置，包括：

确定模块，用于确定起始节点、真实目标节点、预设虚假目标节点和多个中间节点；

获取模块，用于基于最短路径规划模型和识别方行为模型，获取给定观测情形下的候选节点集合在每个中间节点位置处的后验概率分布，所述候选节点集合包括所述真实目标节点和预设虚假目标节点；

评估模块，用于基于所述后验概率分布，评估中间节点的欺骗量级；

求解模块，用于根据中间节点的欺骗量级，求解预设目标函数下的候选子路径；

组合模块，用于将所述候选子路径组合成欺骗路径，所述欺骗路径以所述起始节点为起始点。

可选的，所述获取模块，具体用于：

利用如下算式，计算所述后验概率分布：

y＝costdifms(s，g，n)；

其中，p(g|n)表示所述后验概率分布，n表示所述候选节点集合，α表示归一化因子，β表示一个预设常数，β大于0，costdifms表示意图的代价差，s表示所述起始节点，g表示所述真实目标节点和所述预设虚假目标节点，n表示最近观测到被识别方的位置，n＝o^|o|，o表示给定观测情形对应的观测序列。

可选的，所述评估模块，具体用于：

基于示伪策略和/或藏真策略、以及所述后验概率分布，评估中间节点的欺骗量级。

应用本发明所示实施例，确定起始节点、真实目标节点、预设虚假目标节点和多个中间节点；基于最短路径规划模型和识别方行为模型，获取给定观测情形下的候选节点集合在每个中间节点位置处的后验概率分布，候选节点集合包括真实目标节点和预设虚假目标节点；基于后验概率分布，评估中间节点的欺骗量级；根据中间节点的欺骗量级，求解预设目标函数下的候选子路径；将候选子路径组合成欺骗路径，欺骗路径以起始节点为起始点；可见，本方案提供了一种自动规划出欺骗路径的方案，不依赖人工经验。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例提供的一种欺骗路径生成方法的流程示意图；

图2为本发明实施例提供的一种欺骗路径生成装置的结构示意图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚明白，以下结合具体实施例，并参照附图，对本发明进一步详细说明。

需要说明的是，本发明实施例中所有使用“第一”和“第二”的表述均是为了区分两个相同名称非相同的实体或者非相同的参量，可见“第一”“第二”仅为了表述的方便，不应理解为对本发明实施例的限定，后续实施例对此不再一一说明。

为了达到上述目的，本发明实施例提供了一种欺骗路径生成方法及装置，该方法及装置可以应用于各种电子设备，具体不做限定。下面首先对本发明实施例提供的欺骗路径生成方法进行详细说明。

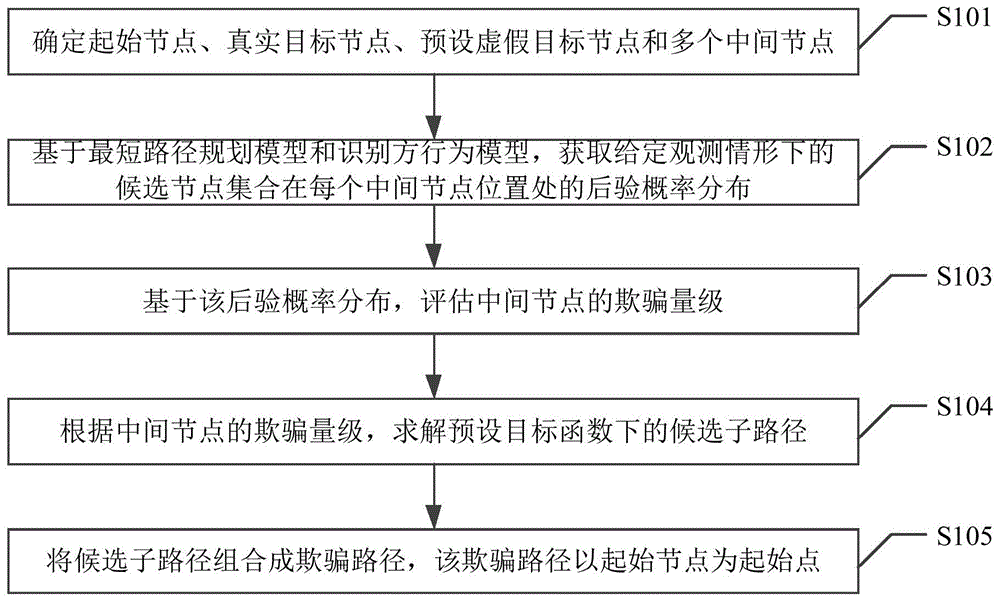
图1为本发明实施例提供的一种欺骗路径生成方法的流程示意图，包括：

s101：确定起始节点、真实目标节点、预设虚假目标节点和多个中间节点。

举例来说，真实目标节点可以理解为路径的真实终点，预设虚假目标节点可以理解为用于迷惑识别方的虚假终点。需要生成欺骗路径时，起始节点和真实目标节点是已知的；可以基于实际地理情况，预先设定虚假目标节点。

一般来说，生成的欺骗路径位于一个区域中，该区域可以为一个城市，一个省份，或者其他行政区域，或者也可以基于实际地理情况，预先设定欺骗路径所在的区域。将该区域进行划分得到多个中间节点，比如，可以将该区域进行均匀划分，每1公里划分一个节点，这些节点即为中间节点，或者说，中间节点可以理解为该区域中划分的最小单元。由于本方案规划的是欺骗路径而不是最优路径，区域中的各个位置都有可能成为欺骗路径中起始节点与真实目标节点之间的节点，因此，可以将区域中的最小单元都作为中间节点。

s102：基于最短路径规划模型和识别方行为模型，获取给定观测情形下的候选节点集合在每个中间节点位置处的后验概率分布，所述候选节点集合包括所述真实目标节点和预设虚假目标节点。

最短路径规划模型和识别方行为模型为预先获取到的，具体获取方式不做限定。

一种实施方式中，可以利用如下算式，计算所述后验概率分布：

其中，p(g|o)表示所述后验概率分布，g表示所述候选节点集合，o表示给定观测情形对应的观测序列，α表示归一化因子，β表示一个预设常数，β大于0，s表示所述起始节点，g表示所述真实目标节点和所述预设虚假目标节点，costdifrg表示意图的代价差，optc表示被识别者行为与观测o一致时从s到g而产生的最优代价，表示被识别者行为与观测不一致时从s到g而产生的最优代价。意图也就是可能的目标节点，包括真实目标节点和预设虚假目标节点。

本实施方式中，可以根据被识别者在两种条件下实现其意图的代价差(costdifference)，定义意图的后验概率：一种是被识别者行为与观测一致而产生的代价、另一种则是不一致产生的代价，参见上述式2。

代价差越小，该意图是真实意图的概率越大，因此可以通过对比不同意图的代价差，生成可能意图集合(候选节点集合)上的概率分布。比如，可以采用玻尔兹曼分布(boltzmanndistribution)假设，即：

由此通过上述式1和式2，可以得到可能意图集合(候选节点集合)的后验概率分布。

或者，另一种实施方式中，可以分别确定每个意图下，符合与不符合(或部分不符合)观测的两条最优路径间的代价差，代价差反映了每个节点的意图不确定性。这种实施方式中，后验概率分布表示为p(g|n)，n包括所述起始节点s、所述候选节点集合g和中间节点，

y＝costdifms(s，g，n)；

其中，p(g|n)表示所述后验概率分布，n包括所述起始节点s、所述候选节点集合g和中间节点，α表示归一化因子，β表示一个预设常数，β大于0，costdifms表示意图的代价差，s表示所述起始节点，g表示所述真实目标节点和所述预设虚假目标节点，n表示最近观测到被识别方的位置，n＝o^|o|，o表示给定观测情形对应的观测序列。

costdifrg和costdifms分别表示不同算法计算得到的意图的代价差，角标rg和角标ms可以理解为不同的算法标识。

本实施方式中，可以将路径规划问题域定义为三元组d＝<n，e，c>，其中，n是非空的节点集合，n包括起始节点s、候选节点集合g和中间节点；e是节点间边的集合；c表示通过每条边的具体代价。

在路径规划问题域中，路径π表示为节点序π＝no，n1……nk，从而对于每个节点i∈0,1……k-1；(ni,ni+1)∈e。πⁱ表示路径π的第i个节点。|π|表示路径长度，同样也是路径π中边的数目，π^|π|＝nk。路径π的代价cost为通行所有边的代价，即所有路径的集合定义为π，所有始于节点π⁰＝n1，终止于π^|π|＝n2的路径集合为π(n1,n2)。

可以将一个路径规划问题定义为一个<d，s，g>三元组，其中，d＝<n，e，c>，d为上述路径规划问题域，s∈n，s表示起始节点，g∈n，g表示目标节点(真实目标节点和预设虚假目标节点)。

路径规划问题的解或解路径是对应问题域d，满足π⁰＝s和π^|π|＝g的路径π。这些路径解的集合为π(s,g)。最优路径是所有解路径中代价最小路径。两个节点之间的最优代价是这两个节点之间的最优路径代价，节点ni到nj的最优代价定义为optc(ni,nj)。可以采用a*算法(a-staralgorithm，一种静态路网中求解最短路径的直接搜索方法)确定最优路径。

在路径规划中考虑欺骗行为，可以理解为存在某敌对的观察者试图了解路径走向。下面给出路径规划问题域中的概率意图识别问题，即元组<d，g，s，o，prob>，其中，d为上述路径规划问题域，表示意图集合，也就是候选节点集合，s∈n，s表示起始节点，o＝o1……om∈n，其中，m大于0，o表示观测序列，prob表示目标节点的先验概率，可以假设其是等概率的。

意图的概率分布g：pr(g|o)为上述问题的解，表示给定观测序列o时g∈g为真实目标的概率。gr∈g表示被识别方的真实意图，或者说gr表示真实目标节点，解的质量由其能否在所有g∈g\{gr}中保证pr(gr|o)≥pr(g|o)来决定。

s103：基于该后验概率分布，评估中间节点的欺骗量级。

欺骗路径规划试图最小化其真实目标节点被识别出的概率。

一个欺骗路径规划(deceptivepathplanning，dpp)问题可以表示为元组<<d,s,gr>,g,p>，其中：

<d,s,gr>表示一个路径规划问题，其中d＝<n，e，c>，d为上述路径规划问题域，s∈n，s表示起始节点，表示意图集合，也就是候选节点集合，p(g|o.n)表示给定观测序列o时目标节点(真实目标节点和预设虚假目标节点)的后验概率，p表示上述最短路径规划模型和识别方行为模型。

欺骗是“所感知现实的扭曲”，并有两种实现方式：“示伪”和“藏真”，又或称为“否定”和“欺骗”，其中，示伪可以理解为：给观察者以一种将机动到其他目标的印象；藏真可以理解为：使规划者模糊其真实目标。

dpp问题的解即规划得到具有欺骗性的路径，而解的质量可用量级、密度和程度三个不同指标进行衡量。

路径中某一步是真实的(truthfulstep)，当且仅当，在该节点处真实目标概率gr大于其他可能目标点的概率，即所有g∈g\{gr}，p(gr|o.n)>p(g|o.n)。否则该步是欺骗性的。

当某一个虚假目标节点的概率严格大于真实目标节点gr概率时，是示伪(simulation)性欺骗。即存在g∈g\{gr}，使得p(gr|o.n)<p(g|o.n)。

可以根据虚假目标节点支配真实目标节点的程度定量化描述示伪性。支配程度越高，示伪性欺骗越强。

其中，o表示给定观测情形对应的观测序列，n表示最近观测到被识别方的位置，n＝o^|o|，gr表示所述真实目标节点，p(g|o)表示所述后验概率分布。simulation(o.n)表示位置n对应的、基于示伪策略得到的欺骗量级。n可以理解为一个点位，一个中间节点也可以理解为一个点位，将中间节点与n进行对应，便得到了中间节点的欺骗量级。

如果示伪欺骗策略成功，识别方将只能把资源部署到错误的位置上去。

当真实目标节点gr的概率与其他虚假目标节点概率差值小于某阈值τ时，是藏真(dissimulation)性欺骗。即存在g∈g\{gr}，使得|p(gr|o.n)-p(g|o.n)|<τ。

严格的藏真欺骗发生于τ＝0时，意味着存在一个虚假目标节点其识别概率与真实目标节点概率一致。由于这种情况在概率化模型中出现次数极少，可以允许藏真欺骗在一个可接受区间内发生，例如真实目标的后验识别概率相对于其他假目标不具有支配性。可以采用香农熵(shannon'sentropy)定量化描述藏真欺骗：

dissimulation(o.n)表示位置n对应的、基于藏真策略得到的欺骗量级。n可以理解为一个点位，一个中间节点也可以理解为一个点位，将中间节点与n进行对应，便得到了中间节点的欺骗量级。

若藏真策略成功，识别方将由于不同意图具有相似的后验概率，无法判断资源的部署位置。此时，识别方将在不存在任何观测信息的假设下进行决策。

一种实施方式中，可以基于示伪策略以及所述后验概率分布，评估中间节点的欺骗量级，具体可以包括：

利用式5，评估中间节点的欺骗量级：

另一种实施方式中，可以基于藏真策略以及所述后验概率分布，评估中间节点的欺骗量级，具体可以包括：

利用式6，评估中间节点的欺骗量级：

再一种实施方式中，可以基于示伪策略和藏真策略、以及所述后验概率分布，评估中间节点的欺骗量级具体可以包括：

combi(o·n)＝ω1·simulation(o·n)+ω2·dissimulation(o·n).(式7)其中，o表示给定观测情形对应的观测序列，n表示最近观测到被识别方的位置，n＝o^|o|，gr表示所述真实目标节点，p(gi|o.n)表示所述后验概率分布，g表示所述候选节点集合，simulation表示基于示伪策略得到的欺骗量级，dissimulation表示基于藏真策略得到的欺骗量级，ω1表示预设第一权重值，ω2表示预设第二权重值。ω1和ω2的具体数值可以根据实际情况进行设定，但要求ω1+ω2＝1，combi表示基于示伪策略和藏真策略得到的欺骗量级。

combi(o.n)表示位置n对应的、基于示伪策略和藏真策略得到的欺骗量级。n可以理解为一个点位，一个中间节点也可以理解为一个点位，将中间节点与n进行对应，便得到了中间节点的欺骗量级。

根据意图隐藏或欺骗的主观强度不同，人们通常在其行为中混杂了示伪和藏真两种效果。这种实施方式中，提出一个综合策略：当真实目标节点gr的识别概率不大于其他虚假目标节点识别概率与阈值τ之和时，是综合性欺骗(combination，即示伪与藏真的综合)。即存在g∈g\{gr}，使得|p(gr|o.n)≤τ+p(g|o.n)|。

将这种策略定量化描述为示伪与藏真策略的线性组合，参考上述式7。相比于示伪策略和藏真策略，综合策略更加灵活全面，既可表现虚假意图，又可隐藏真实意图。

s104：根据中间节点的欺骗量级，求解预设目标函数下的候选子路径。

路径规划中的欺骗可以通过最大化其量级曲线下的包裹面积实现：

对于离散场景，式8可表示为：

其中，i表示路径中的节点，δl表示时间片的长度，t表示时刻。

基于与式9类似的思路，下面介绍一种基于欺骗量级的欺骗最大化模型模型，记为mdm-p，在模型求解过程中，存在以下假设条件：动作的结果是确定性的；对于识别双方，行为模型是可观测的；欺骗方在欺骗路径规划中是理性的。

该模型的数学形式为：

问题：在有向网络n中沿s-gr路径有资源约束地最大化欺骗的量级期望；有向网络n可以理解为上述生成的欺骗路径所在的区域。

参数：i∈n，i表示是网络中的节点(包括起始节点s、g＝{gr、g1……g|g|-1}，g表示候选节点集合，gr表示真实目标节点，g中其他节点为预设虚假目标节点，k＝(i，j)∈e表示网络中的边，j表示网络中的另一个节点，k∈fs(i)表示节点i的出边集合，k∈rs(i)表示节点i的出边集合。

数据：magk表示边k上的欺骗量级值，-∞<magk<+∞；rk大于0，rk表示通行边k所需要的资源，也即边的初始长度；r表示s-gr路径的可用资源总量。

变量：若边k被通行，则xk＝1，否则xk＝0。

基于量级的欺骗最大化模型为：

(目标函数)；

其中，x＝{x∈{0，1}^|e||r^tx≤r}，式10可以理解为约束条件。欺骗方(被识别方)在资源约束r下，沿着路径s-gr最大化欺骗的期望量级。mdm-p的目标函数可以理解为：以欺骗量级最大为目标的函数。

在路径规划领域，网络中的边可以视为动作，因此在上述模型中，边k＝(i,j)的欺骗量级与节点j上的欺骗量级相同，这样，可以把定义在节点上的欺骗量级，转换到网络中的边或动作上。上述约束条件是流量平衡约束，保证优化生成的路径从节点s开始，至gr终止。另外，上述约束条件也保证集合n\{s、g1……gm}中节点i的访问与离开次数相同。

应用上述模型mdm-p的优势有以下几点：一，使用量级指标定量化描述每个节点上的欺骗，为后续不同的欺骗策略提供了一个公共的计算基础，从而拓展了模型在不同场景下的适应性；第二，将欺骗量级定义在节点上，允许欺骗路径以一种全局方式在完整网络上规划。

下面再介绍其他两种模型mdm-p1和mdm-p2：

其中，mdm-p1可以为：

(目标函数)；

约束条件参考上述式10。mdm-p模型的目标函数只要求期望量级的最大化，但约束条件(式10)无法保证优化产生的边与完整路径相连。而mdm-p1通过重构mdm-p为双目标优化问题，可以解决这一问题。

mdm-p2可以为：(目标函数)；

约束条件参考上述式10。mdm-p2同样解决了上述mdm-p中的问题。而且mdm-p2模型的优化复杂度低于mdm-p1模型的优化复杂度，使用mdm-p2模型求解的计算量较低，效率较高。

mdm-p1和mdm-p2的目标函数可以理解为：以欺骗量级最大以及路径最长为目标的函数。

上述mdm-p、mdm-p1和mdm-p2等模型的计算结果为优化后的变量x，x中的非零元素表示欺骗者通行的边，这些边组成欺骗路径，因此将这些边称为候选子路径。

s105：将候选子路径组合成欺骗路径，所述欺骗路径以所述起始节点为起始点。

假设s104中求解得到的候选子路径组成集合e’。如果不存在环路，给定起始节点s和真实目标节点gr，通过端到端的方式即可生成欺骗路径；比如，假设e’＝{(s，n1)，(n1，n2)，(n2，gr)}，则对应的路径为s→n1→n2→gr。

但欺骗路径中大多都存在环路，一种实施方式中，可以基于预设环路条件，识别所述候选子路径组合成的环路；基于所述起始节点、所述真实目标节点、以及识别出的环路，生成由候选子路径组成的欺骗路径。

一种实施方式中，可以遍历所有可能覆盖集合e’的边的顺序组合。例如，假设e’＝{(s，n1)，(n1，n3)，(n1，n2)，(n2，n1)，(n3，gr)}，则通过遍历所有可能的边的顺序组合，得到路径s→n1→n2→n1→n3→gr。但如果欺骗路径中存在多条环路，则利用遍历的方式则复杂度较高。

发明人发现，环路的出现满足以下条件：

|fs(s)|-|rs(s)|＝1，且|fs(s)|＞1；或

|fs(gr)|-|rs(gr)|＝-1且|rs(gr)|＞1；或

|fs(i)＝|rs(i)|＞1，其中n′为边集e′出现的节点集合。

可以识别满足以上条件的节点，将这些节点纳入集合n”，也就是说，n”中的节点位于欺骗路径的环路中。

由于满足i∈n”\{gr}，|fs(i)|＝2，以及i＝gr时|fs(i)|＝1的情况时，总会存在一条边j∈fs(i)，该边的末节点存在一条返回节点i的路径；因此，对于节点i∈n”\{gr}，总存在|fs(i)|-1(或i＝gr，i，gr∈n时，|fs(i)|)个数目的不同路径轨迹，从边e∈fs(i)的末节点返回i。

一种实施方式中，在遇到节点i∈n”时，可以首选寻找一条从集合fs(i)某条边的末节点到节点i的可通行路径，并将这些路径上覆盖的边加入到有序边集中，循环该步骤直到fs(i)中不存在可返回节点i的元素。

举例来说，可以采用如下方式，识别所述候选子路径组合成的环路：

假设给定原始路网d＝<n，e，c>、起始节点s、真实目标节点gr和候选节点集合g的情况下，从优化结果x辨识出带有环路的欺骗路径。首先从d和x中抽取子路网d'＝(n',e',c')，初始化有序边集path。在集合e'中所有的边都被加入path时，识别过程才会终止。对于不处于带环路路径轨迹上的节点，可以通过端对端的方式将其加入到pat}中。而对于正处于环路上的节点，根据上述条件的判断，生成所有从fs(temp)某条边的末节点j出发的路径轨迹，并将轨迹覆盖边的集合coveredgeset加入到path中。对于这两种情况(不处于带环路路径轨迹上的节点和正处于环路上的节点)，都需要继续执行额外的两个步骤：其一，从集合e'中删除已覆盖边；第二，将temp定位到新的节点。

这样，得到了最终生成的欺骗路径。

应用本发明图1所示实施例，确定起始节点、真实目标节点、预设虚假目标节点和多个中间节点；基于最短路径规划模型和识别方行为模型，获取给定观测情形下的候选节点集合在每个中间节点位置处的后验概率分布，候选节点集合包括真实目标节点和预设虚假目标节点；基于后验概率分布，评估中间节点的欺骗量级；根据中间节点的欺骗量级，求解预设目标函数下的候选子路径；将候选子路径组合成欺骗路径，欺骗路径以起始节点为起始点；可见，本方案提供了一种自动规划出欺骗路径的方案，不依赖人工经验。

与上述方法实施例相对应，本发明实施例还提供了一种欺骗路径生成装置，如图2所示，包括：

确定模块201，用于确定起始节点、真实目标节点、预设虚假目标节点和多个中间节点；

获取模块202，用于基于最短路径规划模型和识别方行为模型，获取给定观测情形下的候选节点集合在每个中间节点位置处的后验概率分布，所述候选节点集合包括所述真实目标节点和预设虚假目标节点；

评估模块203，用于基于所述后验概率分布，评估中间节点的欺骗量级；

求解模块204，用于根据中间节点的欺骗量级，求解预设目标函数下的候选子路径；

组合模块205，用于将所述候选子路径组合成欺骗路径，所述欺骗路径以所述起始节点为起始点。

作为一种实施方式，获取模块202具体用于：

利用如下算式，计算所述后验概率分布：

y＝costdifms(s，g，n)；

其中，p(g|n)表示所述后验概率分布，n表示所述候选节点集合，α表示归一化因子，β表示一个预设常数，β大于0，costdifms表示意图的代价差，s表示所述起始节点，g表示所述真实目标节点和所述预设虚假目标节点，n表示最近观测到被识别方的位置，n＝o^|o|，o表示给定观测情形对应的观测序列。

作为一种实施方式，评估模块203具体用于：

基于示伪策略和/或藏真策略、以及所述后验概率分布，评估中间节点的欺骗量级。

上述实施例的装置用于实现前述实施例中相应的方法，并且具有相应的方法实施例的有益效果，在此不再赘述。

所属领域的普通技术人员应当理解：以上任何实施例的讨论仅为示例性的，并非旨在暗示本公开的范围(包括权利要求)被限于这些例子；在本发明的思路下，以上实施例或者不同实施例中的技术特征之间也可以进行组合，步骤可以以任意顺序实现，并存在如上所述的本发明的不同方面的许多其它变化，为了简明它们没有在细节中提供。

另外，为简化说明和讨论，并且为了不会使本发明难以理解，在所提供的附图中可以示出或可以不示出与集成电路(ic)芯片和其它部件的公知的电源/接地连接。此外，可以以框图的形式示出装置，以便避免使本发明难以理解，并且这也考虑了以下事实，即关于这些框图装置的实施方式的细节是高度取决于将要实施本发明的平台的(即，这些细节应当完全处于本领域技术人员的理解范围内)。在阐述了具体细节(例如，电路)以描述本发明的示例性实施例的情况下，对本领域技术人员来说显而易见的是，可以在没有这些具体细节的情况下或者这些具体细节有变化的情况下实施本发明。因此，这些描述应被认为是说明性的而不是限制性的。

尽管已经结合了本发明的具体实施例对本发明进行了描述，但是根据前面的描述，这些实施例的很多替换、修改和变型对本领域普通技术人员来说将是显而易见的。例如，其它存储器架构(例如，动态ram(dram))可以使用所讨论的实施例。

本发明的实施例旨在涵盖落入所附权利要求的宽泛范围之内的所有这样的替换、修改和变型。因此，凡在本发明的精神和原则之内，所做的任何省略、修改、等同替换、改进等，均应包含在本发明的保护范围之内。