一种旋转陶瓷基复合材料叶片的模态计算方法与流程

本发明属于复合材料力学分析技术领域，具体涉及一种旋转陶瓷基复合材料叶片的模态计算方法。

背景技术：

陶瓷基复合材料因具有耐高温、密度小等优点，成为未来航空材料的候选者。转子叶片作为航空发动机典型热端部件，运用陶瓷基复合材料可以降低重量并承受更高的涡轮前进口温度。转子叶片在实际工况下，需要承受很大的离心力。一方面，离心力增强了叶片的弹性恢复力，使得叶片各阶固有频率提高。另一方面，陶瓷基复合材料的非线性本构造成旋转过程中的损伤，使得旋转叶片的模态计算区别于普通金属材料。

叶片受离心力作用而产生径向拉应力，在模态分析中将其作预应力处理。事实上，复合材料目前更广泛地被应用在风力机叶片上。yanbincui(cuiy，shil，zhaof.modalanalysisofwindturbineblademadeofcompositelaminatedplates[c]//2010asia-pacificpowerandenergyengineeringconference.ieee，2010.)、zhou，liqun(zhoulq，xingsh，liyp.dynamicanalysisforwindturbinecompositeblade[j].appliedmechanicsandmaterials，2013，364：102-106.)、xingshuaiheng(shuaihengx，liqunz，yupingli，etal.windturbinecompositebladedynamiccharacterresearch[j].journalofmechanicalstrength，2014.)等人均对复合材料风力机叶片进行了模态计算，并分析了铺层角度的影响。zhengguang-hua(guang-huaz，jia-linli，xuet，etal.vibrationmodalanalysisofcompressorbladebasedonansys[j].internationaljournalofplantengineeringandmanagement，2017，22(2).)基于ansys软件对压气机叶片进行了强度和模态计算，分析了离心力对模态参数的影响。qiangyang(yangq，fangkq，shaoc.vibrationcharacteristicsanalysisofaeroenginecompositeblade[j].advancedmaterialsresearch，2012，583：57-61.)使用非接触式激光扫描振动计测量了航空发动机复合材料叶片模态响应，并与fem结果进行了对比分析。目前的工作大多基于有限元软件进行预应力模态计算，研究离心力对叶片模态的影响，但是均未定性、定量地考虑复合材料由于弹性模量下降引起的结构软化现象。因此，确有必要对现有技术进行改进以解决现有技术之不足。

技术实现要素：

本发明针对现有技术中的不足，提供一种旋转陶瓷基复合材料叶片的模态计算方法。

为实现上述目的，本发明采用以下技术方案：

一种旋转陶瓷基复合材料叶片的模态计算方法，其特征在于，包括如下步骤：

步骤1、对陶瓷基复合材料叶片划分有限元网格，并获得单元、结点信息；

步骤2、计算单元动能、应变能，获得离心力载荷下有限元形式的运动控制方程；

步骤3、基于损伤组装结构的弹性刚度矩阵、初应力刚度矩阵、离心力刚度矩阵，以及步骤2计算的运动控制方程，进行离心载荷下的静力分析获得预应力；

步骤4、将预应力加载到结构上进行模态分析，求解广义特征值问题获得离心力载荷下的模态；模态包括固有频率ω和固有振型向量φ。

为优化上述技术方案，采取的具体措施还包括：

进一步地，步骤1中，对陶瓷基复合材料叶片进行有限元网格划分，并提取有限元程序可识别的单元、结点信息；基于有限元原理，组装与应力状态无关的形函数矩阵[n]、质量矩阵[m]、等效离心力载荷{qc}等。

进一步地，步骤2中，计算单元动能te和应变能ue分别为

式中，ρ是材料密度，u是瞬时位移，是瞬时速度，r是旋转单元的初始位置向量，ω是旋转角速度，表示单元绕轴做定转速ω的旋转运动，ve是单元体积，v表示体积，{ε}是单元应变，[d]是弹性矩阵；

代入拉格朗日方程

式中，t表示总体动能，是系统用广义坐标表示的动能，t表示时间，{q}表示广义力，{δ}表示广义位移，即叶片上各节点在离心力作用下的位移；

化简获得有限元形式的运动控制方程

式中，{qc}表示离心力荷载向量；反对称陀螺阵[mg]与旋转角速度ω一次方成正比，对前几阶频率影响较小，可忽略；[ke]是系统弹性刚度矩阵，包括小位移刚度矩阵[k0]和大变形刚度矩阵[kn]，分别为

式中，[b0]是线性几何矩阵，与节点位移无关；[bn]是非线性几何矩阵，是节点位移的函数；e表示单元数；因为是用有限元求解，所以单元的各矩阵需要组装成结构的总体矩阵；所以，这边的方程表示在每个单元内积分获得单元的各矩阵，然后组装成总体矩阵；

初应力刚度矩阵[kσ]是由离心载荷产生的附加刚度矩阵，导致应力刚化现象，由下式给出

式中，矩阵[g]是形函数对坐标的偏导组装的矩阵，与位移无关；矩阵[m]是9×9由六个应力分量组成的矩阵，与应力直接相关；

离心力刚度矩阵[kc]是由旋转引起的对称阵，与旋转角速度ω的二次方成正比，由下式给出

式中，[s]是由单位旋转角速度向量在x、y、z轴上的投影组成的矩阵；

可以表示成ω·[s]。

进一步地，步骤3中，进行离心载荷下的静力分析，对于静力学问题，位移{δ}与时间无关，则其对时间的一阶和二阶偏导均为0，即代入式(4)可得

([ke]+[kσ]-[kc]){δ}＝{qc}(9)

运用牛顿-拉斐逊迭代法求解上式，获得预应力。

进一步地，步骤3中，运用牛顿-拉斐逊迭代法求解上式，具体的迭代过程分成四步：

3-1)选取初始位移{δ}0＝[k0]^-1{qc}，并计算出离心力刚度矩阵[kc]；

32)根据初始位移{δ}0，依次计算出当前应力状态下的初应力刚度矩阵[kσ]和大变形刚度矩阵[kn]；预应力则是由离心载荷引起的，并以初应力刚度矩阵[kσ]的形式，作为附加刚度矩阵出现在控制方程中；

3-3)运用下式进行迭代求解

{δ}i＝([ke]i-1+[kσ]i-1-[kc])^-1{qc}(10)

式中，i表示迭代序号，第i步的位移是由上一步的计算结果得到的；

3-4)规定{δ}i≈{δ}i-1时计算收敛，{δ}i即为旋转态叶片平衡位置的位移；

其中，每一迭代步均考虑弹性模量降低引起的结构软化，区别于一般的线性材料；根据每一步的位移依次计算出当前状态下的应力、应变；进一步获得割线刚度，用于计算各刚度矩阵中反映材料性能的弹性矩阵[d]，实现刚度的实时折减。

进一步地，步骤4中，根据步骤3的结果获得当前转速下的离心应力分布，并以预应力形式对叶片进行模态计算

求解广义特征值问题

([ke]+[kσ]-[kc]-ω²[m]){φ}＝0(12)

式中，ω是模态中的固有频率，{φ}是模态中的固有振型向量，即可获得离心力载荷下陶瓷基复合材料叶片的模态。

本发明的有益效果是：本发明提供的一种旋转陶瓷基复合材料叶片的模态计算方法，综合考虑了由弹性模量下降引起的结构软化和离心力引起的结构刚度加强现象。运用牛顿-拉斐逊法，并在每个迭代步中进行刚度的实时折减，能够给出离心力载荷下陶瓷基复合材料叶片的模态响应和应力、应变响应。相比于现有的计算方法，本发明考虑了陶瓷基复合材料的非线性本构对叶片模态的影响。

附图说明

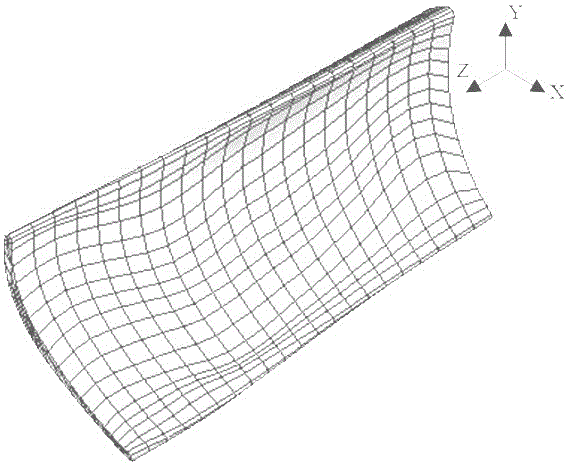
图1本发明中陶瓷基复合材料叶片模型。

图2本发明中陶瓷基复合材料叶片第一阶固有频率与转速关系。

具体实施方式

现在结合附图对本发明作进一步详细的说明。

实施例：对如图1所示的陶瓷基复合材料叶片施加离心载荷，转速ω从0增大到2000rad/s。

步骤1：对陶瓷基复合材料叶片进行有限元网格划分，并提取有限元程序可识别的单元、结点等信息。基于有限元原理，组装与应力状态无关的形函数矩阵[n]、质量矩阵[m]、等效离心力载荷{qc}等。

其中叶片绕着y轴旋转，离心力的等效节点载荷由下式计算

步骤2：推导有限元形式的运动控制方程，并获得方程中各刚度矩阵的计算公式，如式(4)-(8)所示。

步骤3：进行离心载荷下的静力分析获得预应力。静力学问题的控制方程如式(9)所示。运用牛顿-拉斐逊迭代法求解上式，具体的迭代过程分成四步：

3-1)选取初始位移{δ}0＝[k0]^-1{qc}，并计算出离心力刚度矩阵[kc]；

3-2)根据初始位移{δ}0，依次计算出当前应力状态下的初应力刚度矩阵[kσ]和大变形刚度矩阵[kn]；

3-3)运用式(10)进行迭代求解；

3-4)规定{δ}i≈{δ}i-1时计算收敛，{δ}i即为旋转态叶片平衡位置的位移。

上述步骤中，每一迭代步均考虑弹性模量降低引起的结构软化，区别于一般的线性材料。根据每一步中的位移可依次计算出当前状态下的应力、应变。进一步获得割线刚度，用于计算各刚度矩阵中反映材料性能的弹性矩阵[d]，实现刚度的实时折减。

步骤4：根据步骤3中的结果获得当前转速下的离心应力分布，并以预应力形式对叶片进行模态分析。求解广义特征值问题获得离心力载荷下陶瓷基复合材料叶片的模态。

将考虑材料非线性的计算结果和只考虑离心力刚化作用的计算结果绘制在图2中。横坐标为转速；纵坐标为第一阶固有频率。由图2可知，随着离心载荷的增大，第一阶固有频率ω1均增大，表明固有频率受叶片旋转刚度加强效应的影响很大。在较小转速下，材料的损伤不明显，两条曲线几乎无差别。随着转速的增大材料损伤程度加剧，会发现固有频率增大的程度被减弱，是非线性本构造成的结构软化现象的表现。

需要注意的是，发明中所引用的如“上”、“下”、“左”、“右”、“前”、“后”等的用语，亦仅为便于叙述的明了，而非用以限定本发明可实施的范围，其相对关系的改变或调整，在无实质变更技术内容下，当亦视为本发明可实施的范畴。

以上仅是本发明的优选实施方式，本发明的保护范围并不仅局限于上述实施例，凡属于本发明思路下的技术方案均属于本发明的保护范围。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理前提下的若干改进和润饰，应视为本发明的保护范围。