一种基于3D视觉聚类和匹配的机器人乱序目标分拣方法与流程

本发明涉及机器人乱序目标分拣识别方法，特别是涉及一种基于3d视觉聚类和匹配的机器人乱序目标分拣方法。

背景技术：

随着工业机器人在智能分拣、装配制造等领域的广泛应用，企业生产模式逐渐由传统的以人力为主导转向以机器人为主导。传统的分拣方法针对多品种小批量工件主要依靠工人操作，这种方法需要较高的雇佣成本，随持续时间和工作强度的增长，分拣准确率也会受到大幅影响，且由于劳动时限，作业效率不高。随着生产制造业向自动化、智能化和信息化的转型，机器视觉使用成本的逐步降低，搭载视觉装置的机器人分拣系统受到了重点关注。

机械臂分拣系统作为工业机器人技术和计算机视觉技术相结合的智能化设备，能够依靠高度的稳定性和先进的识别算法在复杂的生产环境进行作业。目标分拣识别的方法多基于rgb二维图像，使用canny和sobel算子等提取工件轮廓进行模板匹配，或者提取sift、surf等特征点进行匹配、筛选、滤除等，能够获得较好的识别效果。另一方面，为了更好地适应光照条件变化、应对某些工件纹理不凸显、充分利用几何形状特征等，基于3d视觉的识别算法，逐渐成为了国内外制造企业和研究机构的关注热点。

然而，由于3d点云的有效特征描述子如fpfh、shot、vfh等的识别范围和准确性均有一定的限制，无法很好适应场景多变化和工件多品种、多位姿的生产环境，通用性、普适性的缺失，制约了3d视觉在实际中的广泛应用。3d点云识别主要存在以下问题：①视觉装置通常只获取单一视角的有限数据，且存在工件堆叠、环境约束、传感器性能等引起的点云残缺现象；②某些规则工件的法线一致性较高，多数以法线为基础的点云描述子效用甚微；③形状结构相似的工件特征相近，难以准确识别。

技术实现要素：

发明目的：为了克服上述现有的技术缺陷，提供了一种基于3d视觉聚类和匹配的机器人乱序目标分拣方法。该方法提供了针对分拣过程中多种类、多姿态工件的目标识别和位姿估计算法，具有较强的适应性，能够针对形状结构接近的工件和堆叠无序的摆放场景进行识别估计，满足作业任务的需要，提高机械臂分拣系统的准确性和稳定性。

技术方案：为实现上述发明目的，本发明提供以下技术方案：

一种基于3d视觉聚类和匹配的机器人乱序目标分拣方法，包括以下步骤：

(1)对采集的分拣场景点云通过ransac算法滤除分拣场景点云平面，并采用超体聚类和lccp算法对堆叠分拣场景进行分割点云平面，得到多个种类的分拣场景点云簇；

(2)通过pca计算主轴向量，将分拣场景点云沿主轴方向投影到三维平面，并查询三维点邻域得到各分拣场景点云簇的堆叠状态；

(3)通过拟合一个最小二乘意义下的微切平面，估计分拣场景点云中各点的法线，并利用角度判据提取各分拣场景点云簇和目标模型的边缘；

(4)结合各分拣场景点云簇的堆叠状态和边缘点云生成不同的边缘候选匹配集合，利用super4pcs粗匹配获取初始位姿，再通过icp精匹配进行排序识别和位姿估计。

进一步的，步骤(1)中对于采集的分拣场景点云，首先采用基于随机采样一致性ransac算法对分拣场景背景进行删除，滤除分拣场景点云平面，具体为：

(101)随机从分拣场景点云中抽取子点云样本；

(102)用最小方差计算子点云样本对应的平面方程ax+by+cz＝d的平面模型参数a,b,c,d，其中，x,y,z表示三维点空间坐标变量；

(103)用该模型参数验证剩余点云，计算剩余点云中某一点pi至该平面的距离di＝|axi+byi+czi-d|，其中，xi,yi,zi表示点pi的三维坐标分量；

(104)选取误差范围t，若di≤t则点pi被认为在给定的误差范围内；

(105)如果较多的点在给定误差范围t之内，则该随机选取的样本最优，否则回到步骤(101)，循环进行；

(106)最后根据平面模型参数，滤除场景点云中在误差范围之内的点云子集。

进一步的，步骤(1)中超体聚类具体为：

(111)对输入的分拣场景点云布置规律的区域生长晶核，晶核在空间中均匀分布；

(112)指定晶核半径rseed和晶粒距离，以及最小晶粒的结核范围，控制结晶过程；

(113)然后使所有晶核在点云体素的八叉树中进行搜索，根据体素差异同时吸纳相似晶粒，区域生长从而形成数量较多的超体素块；体素差异公式为：

；

其中，dc、dn、ds分别表示点云体素的颜色差异、法线差异、距离差异，wc，wn，ws分别表示对应的权重，体素差异小于d的吸纳入晶核。

进一步的，步骤(1)中采用lccp算法对堆叠分拣场景进行分割点云平面，具体为：

(121)通过cc和sc判据计算超体聚类得到的超体素块之间的凹凸关系；cc判据利用相邻两面中心连线向量与法向量夹角、相邻两面相交关系进行判断，公式为：

；

；

；

其中，为相邻超体素块质心的法线向量，为相邻超体素块质心位置向量，表示两个相邻超体素块的连接关系，可表示某超体素块的相关属性，其中ni分别为超体素块i的法线向量、与相邻超体素块的边集合，表示基础凸性判据所得的凸性连接判断，表示通过基础凸性判据得到凸性连接判断的推论，β表示相邻超体素块的法线夹角，βthresh为判断相邻超体素块是否为凸性连接的阈值；

sc判据作为补充，判断相邻两面是否真正连通和单独面是否存在，解决cc判据无法区分的情况；将作为相邻两平面法向量的叉乘，公式为：

；

；

；

其中，表示两个相邻超体素块i和j的质心连线向量和法线叉乘向量之间的最小角度，β表示相邻超体素块的法线夹角，表示判断相邻超体素块是否为凸性连接的角度阈值，βoff表示实验得出的角度常值，分别取60°、25°，a表示常系数，取为0.25。表示法线向量和的夹角，表示补充判据(sc)所得的超体素块间凸性连接判断；

最终两相邻面的凹凸性判据为：

；

其中，表示组合ccb判据和cce判据得到的扩展凸性判据(cc)，对相邻超体素块进行凸性连接判断；

(122)在标记完各个超体素块的凹凸关系之后，采用区域增长算法将超体素块聚类成较大的不同物体的点云簇pm，0<m≤c，m∈n，完成点云场景的分割。

进一步的，步骤(2)中首先对分拣场景点云中所有三维坐标点进行中心化处理，利用pca算法计算投影主轴方向，将分拣场景点云投影到三维平面中；具体为：

(201)对于分拣场景点云p＝{pi,0≤i≤n,pi∈r³}，对所有三维坐标点pi进行中心化处理，公式为

(202)计算中心化处理后的分拣场景点云p'的协方差矩阵xx^t；

(203)对协方差矩阵xx^t做特征值分解；

(204)取最小特征值对应的特征向量wmin＝{apca,bpca,cpca}作为投影主轴方向；

(205)任意取参数dpca，构造平面apcax+bpcay+cpcaz+dpca＝0作为投影面，得到投影后的平面点云集q＝{qi,0≤i≤n,qi∈r³}。

进一步的，步骤(2)中查询三维点邻域得到各分拣场景点云簇的堆叠状态的方法为：

投影后的点云以最大分散程度分布在三维平面中，然后遍历平面点云集，对于其中的每一点构造球邻域，当邻域中存在与球心点所属点云簇不同的点时，则判断这两个点云簇堆叠，最后记录所有点云簇的堆叠状态；具体步骤如下：

(211)遍历投影后的平面点云集q，对于其中每一点qi，构造球邻域ui(qi,δ)＝{x|qi-δ<x<qi+δ}；

(212)然后在邻域中进行搜索，当使得且则判定与存在堆叠，其中，为平面点云集q中不同簇的点云，0<m1≤c，0<m2≤c，m1∈n，m2∈n，m1≠m2。

进一步的，步骤(3)中通过拟合一个最小二乘意义下的微切平面，估计分拣场景点云中各点的法线，具体为：

(301)在点云簇pm，0<m≤c，m∈n，中某点pi处，通过它的k个近邻点pij(j＝1,2,…,k)拟合一个最小二乘意义下的微切平面t(pi)，微切平面t(pi)的平面方程表达式为：

aix+biy+ciz+di＝0；

其中，x，y，z表示三维空间坐标变量，ai，bi，ci，di为微切平面t(pi)的参数；

则看出微切平面t(pi)的拟合属于线性最小二乘问题，对应的目标函数为：

；

(302)通过目标函数公式求得微切平面t(pi)参数ai，bi，ci，di，在求解平面法向量时需要对矢量进行单位化处理，即为：

；

所以，pi点处的单位法矢量为：

进一步的，步骤(3)中利用角度判据提取各分拣场景点云簇和待分拣目标模型的边缘，具体为：

(311)对于分拣场景点云簇的每一场景点pi估计单位法线向量

(312)选取正交于法线的任意单位向量叉乘运算得从而在场景点pi处建立坐标系

(313)将pi与近邻域的其它点pj(j＝1,2,…k,j≠i)分别做差，得方向向量：

；

然后计算方向向量在微切平面坐标系下的角度：

；

(314)对于集合a＝{angleij}(j＝1,2,…,k,j≠i)，按照大小顺序排序，再按照如下方式取最大值：

；

如果difi>anglethreshold，则认为场景点pi∈边缘点集b，遍历分拣场景点云中的所有场景点pi(i＝1,2,…n)进行判断，即获取点云边缘b。

进一步的，步骤(4)中结合各分拣场景点云簇的堆叠状态和边缘点云生成不同的边缘候选匹配集合，具体为：

(401)获取分拣场景中各点云的堆叠状态；

(402)如果分拣场景点云不存在堆叠，则定义候选匹配集合l＝{b1,b2,…,bc}，其中bm(m＝1,2,…,c)为场景分割后的各点云簇边缘；

(403)如果某点云pi(1≤i≤c)存在堆叠，则将其对应的边缘bi均匀采样固定的点数，设这个值为num，将bi中采样的每一个点分别作为球心，然后构造球邻域查询最近邻k个点，公式为：

k＝frac·s(0.5<frac<1)；

其中，frac为选取的固定比例，s为bi的总三维点数；

将搜索到的k个近邻点形成点集bij(1≤j≤num)，添加到候选匹配集合中，候选匹配集合为l＝{b1,b2,…,bij,…bc}。

进一步的，步骤(4)中利用super4pcs粗匹配获取初始配准位姿，具体为：

(411)选取四点集对：在候选匹配集合l中依次选取边缘bi，作为源点云，选取模型库中待分拣目标模型的边缘bmodel，作为目标点云，首先从bi中选择三个不同的点，然后以共面不共线原则确定第四个点，组成基e＝{pa,pb,pc,pd}，其中线段papb和pcpd相交于o点，夹角为θ；可得相应比例r1,r2，点距d1,d2如下：

；

；

d1＝||pa-pb||；

d2＝||pc-pd||；

在bmodel中确定集合s1，s2：

s1＝{(qi,qj)|qi,qj∈bmodel,||qi-qj||∈[d1-ε,d1+ε]}；

s2＝{(qi,qj)|qi,qj∈bmodel,||qi-qj||∈[d2-ε,d2+ε]}；

s1，s2中的点对分别满足点距近似为d1,d2的条件，基于仿射不变性的原理，对于s1中的每一对点(qi,qj)，计算由比例r1确定的交点o1，即o1ij＝qi+r1(qj-qi)，同理，对于s2中的每一对点(qi,qj)，计算由比例r2确定的交点o2，即o2ij＝qi+r2(qj-qi)；在s1与s2中搜索满足e1ij与e2ij近似相等的点对，同时满足连线夹角也为θ，这样由(d1,d2,r1,r2,θ)从bmodel中提取出唯一的与基对应的四点集{qa,qb,qc,qd}；

(412)计算位姿变换矩阵：由对应点集{pa,pb,pc,pd}与{qa,qb,qc,qd}计算刚体变换矩阵t，使用t对源点云bi进行变换，统计变换后的点云与目标点云bmodel中最近点距离小于某个阈值δ的点的数目用以表征t的质量，迭代进行上述步骤，直至找到最优的t使得两点云足够接近，此时的变换矩阵记为t0i，作为源点云bi的初始配准位姿，t0i为：

；

其中，r0i为旋转矩阵，t0i为平移向量；

再通过icp精匹配进行排序识别和位姿估计，具体为：

(413)将bi按照初始匹配位姿矩阵t0i变换，公式如下：

bi'＝r0ibi+t0i；

(414)对于bi’中的每一个点pi’，寻找bmodel中最近邻点qi，定义误差函数e(r,t)为：

；

pi'＝rpi+t；

(415)如果误差函数e(r,t)小于给定阈值，或者迭代次数达到设定值，停止迭代计算；否则更新旋转矩阵r和平移向量t继续进行刚体变换，重新计算bi’和e(r,t)，并存储使误差e较小的变换矩阵r、t，直到目标函数emin满足误差要求；

(416)对于候选匹配集合l中的每一边缘bi，在足够的迭代次数之后，得到最终的icp误差集合为{emini}(i＝1,2,…,s)，其中的最小值为：

emin'＝min{emin1,emin2,…,emins}；

识别的结果定义为emin'对应边缘bi的类别，识别目标的位姿依据使误差函数为emin'的变换矩阵估计。

有益效果：与现有技术相比，本发明方法可有效解决机械臂目标分拣作业中的工件目标识别和位姿估计问题，通过对物体的三维感知实现了对具有堆叠、遮挡、乱序等特点的多目标物体的识别、分类和匹配定位，有利于实现工业机器人的自主识别和抓取动作的规划，从而提高搬运、分拣作业的抓取效率和准确程度。

附图说明

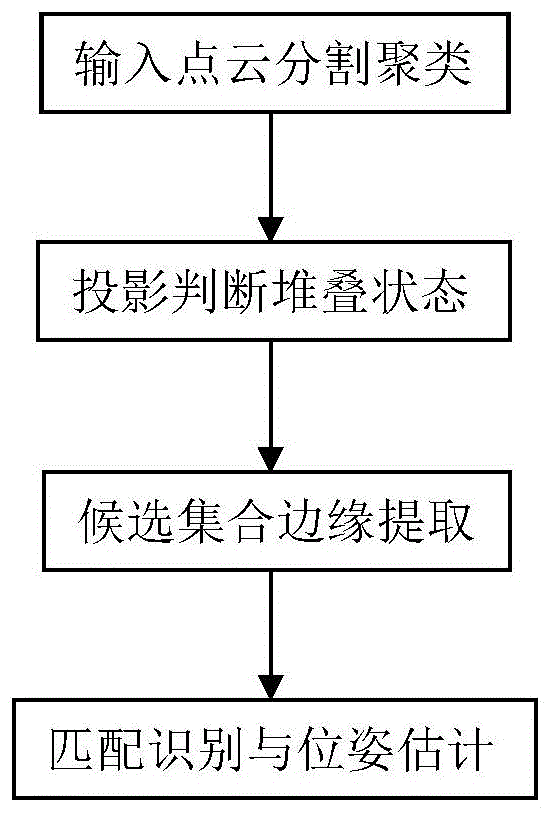
图1为本发明方法总体流程图；

图2为场景点云分割聚类流程图；

图3为超体聚类的模型示意图；

图4为点云簇堆叠状态判断流程图；

图5为边缘点集的提取流程图；

图6为边缘判断的计算示意图；

图7为匹配识别定位流程图。

具体实施方式

下面结合附图和具体实施方式对本发明的技术方案做进一步说明。

图1为本专利所提出的基于3d视觉聚类和匹配的机器人乱序目标分拣方法的总体流程图。算法的具体步骤如下：

1、对采集的分拣场景点云通过随机采样一致性ransac算法滤除分拣场景点云平面，并采用超体聚类和局部凸连接(locallyconvexconnectedpatches，lccp)算法对堆叠分拣场景进行分割点云平面，得到多个种类的分拣场景点云簇；

如图2所示，本步骤分为三个层次执行：对于采集的3d分拣场景点云，首先采用基于随机采样一致性ransac算法滤除平面；然后对分拣场景点云中布置规律的区域生长晶核，根据定义的体素差异公式在点云体素的八叉树中搜索，进行超体聚类；接下来结合扩展凸性判据(extendedconvexitycriterion，cc)和补充判据(sanitycriterion，sc)判断区域的凹凸性，最后用区域增长算法将超体素块聚类成较大的点云簇，并通过局部凸连接算法完成场景点云的分割。

(1)基于随机采样一致性ransac算法滤除平面

本发明采用ransac算法对背景进行删除，该算法的具体步骤如下：

a)随机从分拣场景点云中抽取子点云样本；

b)用最小方差计算子点云样本对应的平面方程ax+by+cz＝d的平面模型参数a,b,c,d，其中，x,y,z表示三维点空间坐标变量；

c)用该模型参数验证剩余点云，计算剩余点云中某一点pi至该平面的距离di＝|axi+byi+czi-d|，其中，xi,yi,zi表示点pi的三维坐标分量；

d)选取误差范围t，若di≤t则点pi被认为在给定的误差范围内；

e)如果较多的点在给定误差范围t之内，则该随机选取的样本最优，保留平面模型参数，否则回到a)步骤，循环进行；

f)最后根据平面模型参数，滤除场景点云中在误差范围之内的点云子集。

(2)场景点云的超体聚类

超体聚类是一种点云预处理的方法，该算法的具体步骤如下：

a)对输入的分拣场景点云布置规律的区域生长晶核，其在空间中均匀分布；

b)如图3所示，指定晶核半径rseed和晶粒距离，以及最小晶粒的结核范围，控制结晶过程；

c)然后使所有晶核在点云体素的八叉树中进行搜索，根据体素差异同时吸纳相似粒子，区域生长从而形成数量较多的超体素块。体素差异公式为：

其中，dc、dn、ds分别表示点云体素的颜色差异、法线差异、距离差异，wc，wn，ws表示对应的权重，体素差异小于d的可吸纳入晶核。

(3)局部凸连接聚类

在获取超体素块的基础上，为了得到种类不同的子点云簇，需要利用局部区域的凹凸性关系进行聚类。具体步骤如下：

a)通过扩展凸性判据(cc)和补充判据(sc)计算超体素块之间的凹凸关系。扩展凸性判据(cc)利用相邻两面中心连线向量与法向量夹角、相邻两面相交关系进行判断，公式为：

其中，为相邻超体素块质心的法线向量，为相邻超体素块质心位置向量，表示两个相邻超体素块的连接关系，可表示某超体素块的相关属性，其中ni分别为超体素块i的法线向量、与相邻超体素块的边集合，表示基础凸性判据所得的凸性连接判断，表示通过基础凸性判据得到凸性连接判断的推论，β表示相邻超体素块的法线夹角，βthresh为判断相邻超体素块是否为凸性连接的阈值。

sc判据作为补充，判断相邻两面是否真正连通和单独面是否存在，解决cc判据无法区分的情况。将作为相邻两平面法向量的叉乘，公式为：

其中，表示两个相邻超体素块i和j的质心连线向量和法线叉乘向量之间的最小角度，β表示相邻超体素块的法线夹角，表示判断相邻超体素块是否为凸性连接的角度阈值，βoff表示实验得出的角度常值，分别取60°、25°，a表示常系数，取为0.25。表示法线向量和的夹角，表示补充判据(sc)所得的超体素块间凸性连接判断。

最终两相邻面的凹凸性判据为：

其中，表示组合ccb判据和cce判据得到的扩展凸性判据(cc)，对相邻超体素块进行凸性连接判断。

b)在标记完各个超体素块的凹凸关系之后，采用区域增长算法将超体素块聚类成较大的物体点云簇pm(0<m≤c,m∈n)，完成点云场景的分割。

2、通过pca主成分分析计算主轴向量，将分拣场景点云沿主轴方向投影到三维平面，并查询三维点邻域得到各分拣场景点云簇的堆叠状态

在对分拣场景点云分割得到不同种类点云簇后，由于堆叠的点云会互相遮挡，引起点云的缺失，进而影响目标识别的准确性，为了适应分拣中多变的工件摆放位姿，需要对堆叠状态判断，进行针对性处理。如图4所示，首先对场景点云中所有三维坐标点进行中心化处理，利用主成分分析算法计算投影主轴方向，将场景点云投影到三维平面中。接下来遍历平面点云集，对于其中的每一点构造较小的球邻域，当邻域中存在与球心点所属点云簇不同的点时，可判断这两个点云簇堆叠，最后记录所有簇的堆叠状态。具体步骤如下：

(1)点云pca投影

首先对分拣场景点云中所有三维坐标点进行中心化处理，利用pca算法计算投影主轴方向，将场景点云投影到三维平面中。具体步骤如下：

a)对于分拣场景点云p＝{pi,0≤i≤n,pi∈r³}，对所有三维坐标点pi进行中心化处理，公式为

b)计算中心化处理后的分拣场景点云p'的协方差矩阵xx^t；

c)对协方差矩阵xx^t做特征值分解；

d)取最小特征值对应的特征向量wmin＝{apca,bpca,cpca}作为投影主轴方向；

e)任意取参数dpca，构造平面apcax+bpcay+cpcaz+dpca＝0作为投影面，得到投影后的平面点云集q＝{qi,0≤i≤n,qi∈r³}。

(2)判断分拣场景各点云的堆叠状态

投影后的点云以最大分散程度分布在三维平面中，接下来遍历平面点云集，对于其中的每一点构造较小的球邻域，当邻域中存在与球心点所属点云簇不同的点时，可判断这两个点云簇堆叠，最后记录所有簇的堆叠状态。具体步骤如下：

a)遍历投影后的平面点云集q，对于其中每一点qi，构造球邻域ui(qi,δ)＝{x|qi-δ<x<qi+δ}；

b)然后在邻域中进行搜索，当使得且则判定与存在堆叠。其中，为平面点云集q中不同簇的点云，0<m1≤c，0<m2≤c，m1∈n，m2∈n，m1≠m2。

3、通过拟合一个最小二乘意义下的微切平面，估计分拣场景点云中各点的法线，并利用角度判据提取各分拣场景点云簇和待分拣目标模型的边缘；

使用全部点云进行识别会存在误匹配的情况，而且过多的三维点数目会降低识别效率、影响实时性，需要先提取出点云簇的边缘。首先对于点云簇中的每一点，进行法线估计。接下来选取正交于每点法线的单位向量，并进行叉乘运算，建立局部点的坐标系，随后利用角度判据判断此点是否属于边缘点集，最后对点云簇中的所有点按照相同方式进行判断，从而提取边缘。该算法的具体步骤如下：

(1)法线估计

对于离散点云表面的法线估计，需要拟合对应点的切平面方程，利用区域总体数据来估计某点的法线特征，具体步骤如下：

a)在点云簇pm(0<m≤c,m∈n)中某点pi处，通过它的k个近邻点pij(j＝1,2,…,k)拟合一个最小二乘意义下的微切平面t(pi)，微切平面t(pi)的平面方程表达式为：

aix+biy+ciz+di＝0(9)；

其中，x，y，z表示三维空间坐标变量，ai，bi，ci，di为微切平面t(pi)的参数。

可以看出微切平面t(pi)的拟合属于线性最小二乘问题，对应的目标函数为：

b)通过式(10)求得微切平面t(pi)参数ai，bi，ci，di，在求解平面法向量时需要对矢量进行单位化处理，即为：

所以，pi点处的单位法矢量为：

(2)边缘提取

如图5所示，点云边缘的提取可以转化为判断各点云簇pm(0<m≤c,m∈n)中所有三维点pi是否属于边缘点集bm，判别的具体步骤如下：

a)对于分拣场景点云簇的每一点pi估计单位法线向量

b)选取正交于法线的任意单位向量叉乘运算得从而在点pi处建立坐标系如图6所示；

c)将pi与近邻域的其它点pj(j＝1,2,…k,j≠i)分别做差，得方向向量：

然后计算方向向量在微切平面坐标系下的角度：

d)对于集合a＝{angleij}(j＝1,2,…,k,j≠i)，按照大小顺序排序，再按照如下方式取最大值：

如果difi>anglethreshold，则认为点pi∈边缘点集b，遍历点云中的所有点pi(i＝1,2,…n)进行判断，即可获取点云边缘b。

4、结合各分拣场景点云簇的堆叠状态和边缘点云生成不同的边缘候选匹配集合，利用快速四点一致性配准算法(super4-pointscongruentsets，super4pcs)粗匹配获取目标边缘点云的初始配准位姿，再通过迭代最近点(iterativeclosestpoint，icp)精匹配进行排序识别和位姿估计。

对于场景中的所有点云簇，首先根据堆叠状态生成不同的候选匹配集合，接下来在候选匹配集合中依次选取边缘作为源点云，提取模型库中待分拣目标模型边缘作为目标点云，使用快速四点一致性配准算法(super4pcs)进行粗匹配，将得到的变换矩阵作为初始配准位姿，遍历候选匹配集合，依次和目标模型边缘进行迭代最近点(icp)精匹配，并基于平均最近邻距离度量进行最优误差排序，获取识别结果和位姿估计矩阵。算法的流程图如图7所示，具体步骤如下：

(1)生成候选匹配集合

对于点云簇之间的堆叠与无堆叠关系，需要针对性生成候选匹配集合，以保证识别算法的普适性和稳定性，具体步骤如下：

a)获取分拣场景中各点云的堆叠状态；

b)如果分拣场景点云不存在堆叠，则定义候选匹配集合l＝{b1,b2,…,bc}，其中bm(m＝1,2,…,c)为场景分割后的各点云簇边缘；

c)如果某点云pi(1≤i≤c)存在堆叠，则将其对应的边缘bi均匀采样固定的点数，设这个值为num，将bi中采样的每一个点分别作为球心，然后构造球邻域查询最近邻k个点，公式为：

k＝frac·s(0.5<frac<1)(15)；

其中，frac为选取的固定比例，s为bi的总三维点数。

将搜索到的k个近邻点形成点集bij(1≤j≤num)，添加到候选匹配集合中。候选匹配集合为l＝{b1,b2,…,bij,…bc}。

(2)super4pcs粗匹配

单独的icp匹配算法具有较高的精确性，但存在一定的缺陷：①匹配耗时较长；②容易陷入局优。所以需要使用基于形状特征的super4pcs匹配算法获取初始位姿矩阵，其原理为利用仿射不变性和共面不共线四点集的刚体变换进行匹配，获取质量表征最高的变换矩阵。具体步骤如下：

a)选取四点集对：在候选匹配集合l中依次选取边缘bi，作为源点云，选取模型库中待分拣目标模型的边缘bmodel，作为目标点云。首先从bi中选择三个不同的点，然后以共面不共线原则确定第四个点，组成基e＝{pa,pb,pc,pd}，其中线段papb和pcpd相交于o点，夹角为θ。可得相应比例r1,r2，点距d1,d2如下：

d1＝||pa-pb||(18)；

d2＝||pc-pd||(19)；

在bmodel中确定集合s1，s2：

s1＝{(qi,qj)|qi,qj∈bmodel,||qi-qj||∈[d1-ε,d1+ε]}(20)；

s2＝{(qi,qj)|qi,qj∈bmodel,||qi-qj||∈[d2-ε,d2+ε]}(21)；

s1，s2中的点对分别满足点距近似为d1,d2的条件，基于仿射不变性的原理，对于s1中的每一对点(qi,qj)，计算由比例r1确定的交点o1，即o1ij＝qi+r1(qj-qi)，同理，对于s2中的每一对点(qi,qj)，计算由比例r2确定的交点o2，即o2ij＝qi+r2(qj-qi)。在s1与s2中搜索满足e1ij与e2ij近似相等的点对，同时满足连线夹角也为θ，这样由(d1,d2,r1,r2,θ)可以从bmodel中提取出唯一的与基对应的四点集{qa,qb,qc,qd}。

b)计算位姿变换矩阵：由对应点集{pa,pb,pc,pd}与{qa,qb,qc,qd}计算刚体变换矩阵t，使用t对源点云bi进行变换，统计变换后的点云与目标点云bmodel中最近点距离小于某个阈值δ的点的数目用以表征t的质量，迭代进行上述步骤，直至找到最优的t使得两点云足够接近，此时的变换矩阵记为t0i，作为源点云bi的初始配准位姿，t0i为：

其中，r0i为旋转矩阵，t0i为平移向量。

(3)icp精匹配

通过迭代最近点(icp)算法的平均最近邻最优误差排序，可以对目标点云进行识别；通过模型点云边缘和目标点云簇边缘的刚体变换，可以估计出位姿矩阵。同时，icp较高的匹配精度保证了算法的可用性。具体步骤如下：

a)在候选匹配集合l中依次选取边缘bi，作为源点云，选取模型库中待分拣模型的边缘bmodel，作为目标点云，并以super4pcs粗匹配得到的t0i作为源点云bi的初始配准位姿；

b)将bi按照初始矩阵t0i变换，公式如下：

bi'＝r0ibi+t0i(23)；

c)对于bi’中的每一个点pi’，寻找bmodel中最近邻点qi，定义误差函数e(r,t)为：

pi'＝rpi+t(25)；

d)如果误差函数e(r,t)小于给定阈值，或者迭代次数达到设定值，停止迭代计算；否则更新旋转矩阵r和平移向量t继续进行刚体变换，重新计算bi’和e(r,t)，并存储使误差e较小的变换矩阵r、t，直到目标函数emin满足误差要求。

e)对于候选匹配集合l中的每一边缘bi，在足够的迭代次数之后，得到最终的icp误差集合为{emini}(i＝1,2,…,s)，其中的最小值为：

emin'＝min{emin1,emin2,…,emins}(26)；

识别的结果定义为emin'对应边缘bi的类别，识别目标的位姿可依据使误差函数为emin'的变换矩阵估计。

应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。本实施例中未明确的各组成部分均可用现有技术加以实现。