一种基于改进K-means算法和新聚类有效性指标的聚类分析方法与流程

本发明属于数据挖掘聚类分析领域，尤其涉及一种基于密度参数计算初始聚类中心和中心点替换方法的改进k-means算法和新聚类有效性指标的聚类分析方法。

背景技术：

聚类分析是研究分类问题的一种统计分析方法也是数据挖掘的一个重要方法。聚类分析的研究主要包括两个方面，即聚类算法的研究和聚类有效性指标的研究。聚类算法将待分析的数据集分为多个类，使得同一个类内的数据具有更高的相似性，不同类之间的数据具有更高的差异性。作为无监督学习方式，聚类算法产生的结果的优劣通常用聚类有效性指标来衡量或者评价。

当前，已有许多聚类算法被提出来并用于对各种类型的数据集进行处理。总体来讲，这些聚类算法可以分为基于划分的聚类算法，基于层次的聚类算法，基于密度的聚类算法，基于网格的聚类算法以及基于模型的聚类算法。k-means算法是一种基于划分的聚类算法。由于k-means算法具有实现简单，准确率高等特点，因此被广泛应用于解决各种领域的数据划分问题。然而，初始聚类中心点的随机选取，会导致传统的k-means聚类算法存在聚类结果不稳定、聚类效率低下、容易出现局部最优解等问题。

聚类有效性是指度量聚类算法产生的聚类结果的有效性。聚类有效性的评价通常由聚类有效性指标来完成。当前，已有的聚类有效性指标可以大体分为三类，即内部有效性指标、外部有效性指标和相对有效性指标。目前常用的有效性指标包含j.c.dunn于1973年提出的dunn指标，tadeuszcaliński等人于1974年提出的ch指标，davidl.davies等人于1979年提出的dbi指标等。这些指标被广泛应用于聚类算法聚类有效性的评估中。然而现有的聚类有效性指标普遍存在计算复杂，适用数据集类型范围狭窄等缺点。

技术实现要素：

发明目的：为了解决现有技术中使用k-means聚类法处理数据不稳定的问题，本发明提供一种基于改进k-means算法和新聚类有效性指标的聚类分析方法。

技术方案:本发明提供一种基于改进k-means算法和新聚类有效性指标的聚类分析方法，包括以下步骤：

(1)输入数据集，所述数据集包含n个数据点，每个数据点包含m维的数值型属性，设定数据集待聚类的簇数上限kmax，kmax为不大于的最大正整数；

(2)计算每两个数据点之间的欧几里得距离；

(3)寻找欧几里得距离中的最大值和最小值，分别记为dmax与dmin；

(4)根据dmax与dmin确定阈值；

(5)统计与各数据点的欧几里得距离小于阈值的数据点个数，作为数据点的密度信息；

(6)标记密度信息为0的点为离群点；(7)定义第一集合，第一集合中包含密度信息不为0的数据点及数据点对应的密度信息；

(8)定义第二集合，从第一集合中选取密度信息最大的数据点和第二大的数据点放入第二集合；从第一集合中移除该两个数据点；

(9)将步骤(8)得到的第二集合中的数据点作为初始的中心点进行k-means聚类；

(10)分别计算数据集中的每个数据点与两个初始聚类中心点的欧几里得距离，选择聚类较近的聚类中心点作为该数据点的中心点类别，并将每个数据点的类标签标记为该中心点类别；

(11)对每个类别内的数据，设置虚拟中心点类标签为类内数据类别，虚拟中心点各维度的坐标信息为类内数据不包含密度信息的各维度坐标信息算术平均值；

(12)若虚拟中心点与真实的数据点重合，则更新该类别的聚类中心点为该虚拟中心点；若虚拟中心点与数据点不重合，则更新该类别的聚类中心点为类内距离虚拟中心点最近且距离离群点最远的点；

(13)计算更新后的聚类中心点与更新前的聚类中心点之间的欧几里得距离，若为0则聚类完成，执行步骤(14)；若不为0跳转执行步骤(10)；

(14)根据聚类结果计算聚类有效性指标的值；

(15)统计第二集合中的聚类中心点个数，若聚类中心点个数小于kmax，则从第一集合中选取密度信息最大的数据点放入第二集合，作为新的聚类中心点，然后从第一集合中移除该数据点并跳转步骤(9)；否则执行步骤(16)；

(16)输出在聚类有效性指标最佳时的聚类结果。

进一步的，步骤(1)中，每个数据点具有m维属性，记数据集为d＝{x1,x2,…,xn}，xi表示第i个数据点；记数据点为xi＝(xi1,xi2,…,xim)，xij表示第i个数据点的第j维属性。

进一步的，步骤(2)中，第i个数据点xi与第j个数据点xj之间的欧几里得距离d(xi,xj)的计算方法为：

进一步的，步骤(4)中，设阈值为ε，根据dmax与dmin确定阈值ε的方法为：

ε＝(dmax+dmax)/(2*kmax)

其中kmax为数据集待聚类的簇数上限。

进一步的，步骤(5)中，数据点xi的密度信息ρ(xi)为：

进一步的，步骤(10)中，数据点xi的类标签的确定方法为：计算数据点xi与第二集合中每个聚类中心点si的欧几里得距离，首先计算xi与第一个聚类中心点s1的欧几里得距离，记为d(xi,s1)，并设dmin(xi,s)＝d(xi,s1)，将xi的类标签设为s1的标签，依次计算数据点xi与第二集合中余下k-1个聚类中心点的欧几里得距离，若欧氏距离d(xi,sj)小于dmin(xi,s)，则更新dmin(xi,s)＝d(xi,sj)，并将xi的类标签设为sj的标签，否则保持dmin(xi,s)与xi的类标签不发生变化直到计算完第二集合中所有的聚类中心点。

进一步的，步骤(12)中，设虚拟中心点为si'，若虚拟中心点与数据点不重合，将类标签与虚拟中心点相同的数据点按照欧几里得距离d(xi,si')大小进行排序获得数组din(xi,si')，依次选取数组din(xi,si')中的点，若该点与离群点xj最小距离dminout(xi,xj)小于虚拟中心点与离群点xn最小距离dminout(si',xn)，则选取该点作为新的聚类中心点，否则选取数组din(xi,si')内下一个距离虚拟中心点最近的点重复此过程。

进一步的，步骤(14)具体包括：设在更新前的第二集合为si，设在更新后的第二集合为sj，集合si与集合sj均包含q个数据点，每个数据点包含m个属性值，则对应的两次迭代聚类中心点的集合的欧氏距离为：

若欧氏距离为0，则表示两次迭代聚类中心点未发生变化，停止迭代；否则重复执行步骤(10)。

进一步的，步骤(14)中，根据聚类结果计算聚类有效性指标的计算方法为：将数据集划分成k个类c＝{c1,c2,…,ck}，其中第k个类包含的样本点个数为|ck|，该类的聚类中心点为ck，则第k个类的类内相似度为：数据集的全局类内相似度为：

数据集的全局类间分离度为：

聚类有效性指标函数dcvi(k)为：

进一步的，步骤(16)中聚类有效性指标最佳指聚类有效性指标函数值最小。有益效果：本发明提供一种基于改进k-means算法和新聚类有效性指标的聚类分析方法，相比较现有技术，存在以下优点：

(1)高密度初始中心点的选取降低了k-means聚类算法的迭代次数，从而减少了聚类算法的时间消耗，提升了聚类效率。

(2)高密度初始中心点的选取和中心点替换方法的结合降低了k-means聚类算法陷入局部最优解的可能性。

(3)本方法不会受随机因素影响，聚类结果稳定。

(4)新的聚类有效性指标综合考量聚类结果类内相似度与类间分离度，能够很好地评价聚类算法的聚类结果，使得到的聚类结果更准确。

附图说明

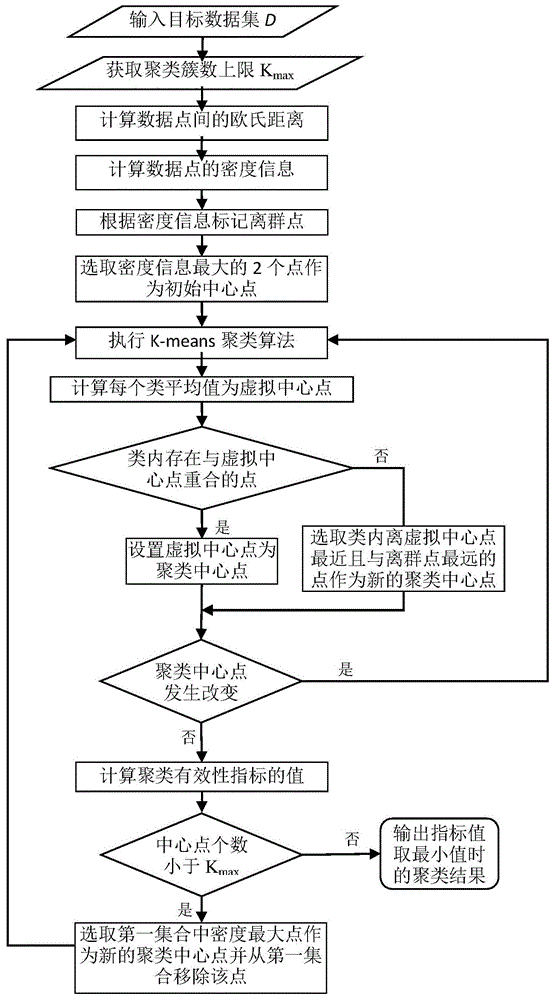
图1为本发明的整体流程图；

图2为本发明获取数据点密度信息流程图；

图3为本发明中改进k-means算法执行流程图。

具体实施方式

下面结合具体实施例和附图对本发明作进一步说明。

如图1所示，一种基于改进k-means算法和新聚类有效性指标的聚类分析方法，包括以下步骤：

(1)输入数据集d，确定数据集待聚类的簇数上限kmax，所述数据集d包含n个数据点。每个数据点具有m维属性且各维属性都是数值型数据，记数据集为d＝{x1,x2,…,xn}，xi表示第i个数据点；记数据点为xi＝(xi1,xi2,…,xim)，xij表示第i个数据点的第j维属性。聚类簇数上限kmax为不大于的最大正整数。

(2)计算数据集d中的每两个数据点之间的欧几里得距离，即欧氏距离。若数据集d中的数据包含m个属性，则对于数据集d中的样本点xi与xj，二者之间的欧几里得距离的计算公式为：

(3)寻找欧几里得距离中的最大值和最小值，分别记为dmax与dmin，即

(4)根据dmax与dmin确定阈值ε，用于统计样本点密度信息，阈值ε计算公式为：

ε＝(dmax+dmin)/(2*kmax)；

(5)如图2，统计与各数据点的欧几里得距离小于阈值的数据点个数，作为数据点的密度信息；计算数据点xi与第二集合s中每个数据点si的距离，若距离d(xi,si)小于之前的最小距离，则更新最小距离并将数据点xi的标签设为si的标签。数据点的密度信息的计算公式为：

(6)标记密度信息为0的点为离群点。

(7)定义空的第一集合t，将数据集d中密度信息不为0的的数据点与对应数据点的密度信息放入第一集合t；

(8)定义空的第二集合s，从第一集合中选取密度信息最大的数据点和第二大的数据点放入第二集合，作为初始聚类中心点；并从第一集合中移除该两个数据点；

(9)将步骤(8)得到的第二集合中的数据点作为初始的中心点进行k-means聚类；

如下为改进的k-means聚类算法，利用了k-means算法高质量的初始中心点能降低聚类算法迭代次数的优点，减少了聚类算法的时间消耗；基于密度参数计算初始聚类中心和中心点替换方法的引入提高了k-means算法的聚类准确度；提出的新聚类有效性指标dcvi综合考量了聚类结果类内相似度与类间分离度，能够很好地评价聚类算法的聚类结果。因此本发明能获得准确且稳定的聚类结果。具体参见图3流程图。

(10)计算数据点xi与第二集合s中每个聚类中心点si的距离，首先计算xi与第一个中心点s1的距离，记为d(xi,s1)，并设dmin(xi,s)＝d(xi,s1),将xi的类标签设为s1的标签。依次计算数据点xi与第二集合s中余下k-1个聚类中心点的欧氏距离，若欧氏距离d(xi,sj)小于dmin(xi,s)，则更新dmin(xi,s)＝d(xi,sj)，并将xi的类标签设为sj的标签，否则保持dmin(xi,s)与xi的类标签不发生变化；

(11)统计数据集d中与si标签相同的数据点信息，对获取的数据点信息求平均，获得的数据信息即为新的虚拟中心点si'的信息。k-means聚类算法中对象的属性值为数值型(连续性)数据，则均值其中n为属于该类的记录总数，bi为属性值；

(12)若得到的虚拟中心点与真实的样本点重合，则该点即为该类的聚类中心，否则将类标签与si'相同的点按照距离d(xi,si')进行升序排序获得数组din(xi,si')，依次选取数组din(xi,si')中的点，若该点与离群点xj最小距离dminout(xi,xj)小于虚拟中心点si'与离群点xn最小距离dminout(si',xn)，则选取该点作为新的聚类中心点si，否则选取数组din(xi,si')内下一个距离虚拟中心点最近的点重复此过程直到获取所有新的聚类中心点。

(13)计算新的聚类中心点与前一次迭代的聚类中心点之间的欧氏距离，即：若欧氏距离为0则停止迭代，否则跳转到步骤(10)；

(14)根据聚类结果计算聚类有效性指标的值。

若改进k-means聚类算法将目标数据集划分成k个类c＝{c1,c2,…,ck}，其中第k个类包含的样本点个数为|ck|，该类的聚类中心点为ck，则第k个类的类内相似度为：数据集的全局类内相似度为：

数据集的全局类间分离度为

聚类有效性指标函数dcvi(k)为：

(15)统计第二集合中的聚类中心点个数，若聚类中心点个数小于kmax，则从第一集合中选取密度信息最大的数据点放入第二集合，作为新的聚类中心点，然后从第一集合中移除该数据点并跳转步骤(9)；否则执行步骤(16)；

(16)聚类有效性指标函数值最小时的聚类结果为最佳聚类结果，最佳聚类数(kopt)的确定方法为：