一种基于二进制引力搜索的节能虚拟机放置方法与流程

本发明涉及二进制引力搜索的节能虚拟机放置方法，属于节能优化的云计算领域。

背景技术：

云计算模式近些年成为了可伸缩计算资源和按需服务的新模型，也称为“随用随付”模型。这些服务提供给用户三个级别访问方式，即基础架构即服务(iaas)，平台即服务(paas)和软件即服务(saas)。一方面，计算资源比以前便宜，另一方面，它们的性能更高。在这种模式下，终端用户或消费者将获得计算资源，例如cpu运行时间和网络上的存储，同时提供商按照定价模型管理资源向消费者的分配。亚马逊，微软，谷歌和阿里巴巴等it行业的领导者现在提供了几种云计算业务模型以吸引潜在的消费者。还应注意的是，公司倾向于在云上选择和构建他们的it系统，其中51％的公司声称他们已经建立了新的策略。云计算使这些公司降低了硬件障碍并为创新提供更多机会。借助云计算，提供商可以提供满足消费者需求的服务，而无需任何额外要求和适当的价格。同时，资源可扩展且易于扩展。但与云计算成功相关的主要副作用是能源消耗的增长。它增加了为设备供电和冷却的能源成本，统计显示，数据中心能源消耗的来源是基础设施、服务器和存储设备等。在这样的模型中，使用硬件设备会释放更多的热量，并且直接影响冷却系统的能耗，对经济和环境产生了不好影响。为了解决这些问题，绿色信息技术生态学应运而生，并开启了新的研究课题。文献号为cn102929687的现有技术公开了一种节能的云计算数据中心虚拟机放置方法，包括：a.建立物理服务器区域；b.获取物理服务器信息；c.计算待创建虚拟机资源；d.对物理服务器进行排序；e.建立待创建虚拟机与物理服务器之间的映射；f.判断是否有单个物理服务器满足需求；g.判断是否存在同一分区内的满足要求的物理服务器序列；h.选取空调能耗成本最小、且物理服务器数量最少的服务器序列。本发明的云计算数据中心虚拟机放置方法，优先选用单个物理服务器来创建虚拟机，再选用同一分区内的物理服务器来创建虚拟机；在前两者都不存在的情况下，最终选用集中程度最高的物理服务器序列来创建虚拟机，实现云计算中心虚拟机的节能放置。该文献侧重于空调制冷系统的节能，对虚拟机放置算法本身研究不够深入，仍有很大的改进空间。

技术实现要素：

本发明的目的是提供一种基于二进制引力搜索的节能虚拟机放置方法，以实现在虚拟机放置降低能耗，同时提高云计算性能。

本发明解决上述技术问题采用的技术方案为：一种基于二进制引力搜索的节能虚拟机放置方法，所述方法采用引力搜索算法来实现，引力搜索算法为：

考虑一个含有n个智能体的系统，用xi定义第i个智能体的位置，

fori＝1，2，…，n

其中x^di代表第i个智能体在第d个维度的位置，

用f^dij(t)表示在t时刻智能体j对i的力，计算公式为：

其中mpi(t)和maj(t)分别为作用粒子j的惯性质量和被作用粒子i的惯性质量，ε是一个很小的常量，g(t)是在t时刻的引力常数；

引力常数g(t)的计算公式为：

其中g0等于100，a等于20，t是系统迭代的次数；

在引力搜索算法中，为了增加随机特性，假设在第d维上作用在第i个智能体上的总的作用力是其他所有智能体作用力的总和，其大小f^di(t)的定义如下：

其中randj是范围0到1间的随机数，是第d维中第j个智能体作用在第i个智能体上的引力；

根据牛顿第二定理，粒子i在第d维上t时刻的加速度adi(t)的计算方法如下：

其中mi(t)是第i个智能体的惯性质量,它是由智能体的适应度计算出来的(适应度已知)，计算公式为：

mai＝mpi＝mii＝mi，i＝1，2，…，n

其中fiti(t)表示在第t时刻，智能体i的适应度，对于求最大值问题，worst即适应度值的最小值，相应的best即为适应度值的最大值，

在所述算法中，对于每一次的迭代过程，智能体都会根据以下公式更新它的速度和位置：

对于小|v^di|，更改x^di的概率必须为接近零,且|v^di|大时，x的概率运动必须很高；

定义s(v^di(t))为转化x^di成概率函数的函数，s(v^di(t))应该限制在区间[0,1]内，并随着s|v^di(t)|的增加而增加，s(v^di(t))的定义为：

s(v^di(t))＝|tranh(v^di(t))|

s(vdi(t))被计算出,将随下列公式移动

结合上述算法实现虚拟机放置的具体步骤：

步骤1:初始化，将服务器资源列表定义为向量，大小为m，m是数据中心中的服务器数量；将虚拟机(vm)列表定义为向量，大小为n，n是数据中心中的服务器数；虚拟机对应上述算法中的智能体，定义代理数和迭代次数；

步骤2：随机设置每个智能体的位置，确保位置在搜索空间中即可；

步骤3：在每次迭代中，我们计算初始位置的所有智能体的适应度，如果本轮迭代中的适应度高于上一轮迭代的适应度，则更新；

步骤4：对于每个智能体，都根据新的适应度计算质量，引力常数也会随着迭代次数的增加而更新，即随着时间的变化，重力值也会随之变化；用新质量和重力值计算加速度；

步骤5：在搜索空间中移动智能体的位置；

至此，完成虚拟机放置。

进一步地，在搜索空间中移动智能体的位置(用于虚拟机放置过程的二进制引力搜索)采用算法为：

输入：vm列表，服务器列表，输出：虚拟机放置最佳位置，过程如下：

1)初始化；2)确定最大迭代次数；3)计算适合度；4)更新适应度；5)计算惯性质量m；6)计算引力常数；7)计算加速度；8)移动虚拟机(代理机)的位置；9)结束迭代；10)返回位置。

进一步地，确定虚拟机(代理机)新位置的算法为：输入：加速度，速度，当前位置；输出：新位置；过程如下：1)计算新速度；2)计算转化x^di成概率函数的函数s，s(v^di(t))的定义为：s(v^di(t))＝|tranh(v^di(t))|；3)产生要完成的动作；4)对于每一个智能体执行5)；5)寻找改变的比特位；更新比特位；更新位置；6)结束；7)返回新位置。

本发明具有以下有益技术效果：

本发明采用二进制引力搜索算法降低虚拟机放置能耗，同时提高云计算性能。因为云计算放置依赖于虚拟化技术，而虚拟化的主要目标是抽象硬件和将物理资源共享给多个虚拟主机(vm)，需要一种计算服务来提供解决方案确保降低能耗，同时提高云计算性能。本发明提出的基于二进制引力搜索的节能虚拟机放置方法，实现了在虚拟机放置降低能耗，同时提高云计算性能。经验证可知，在bgsa中比pso迭代次数少的最佳选择，本发明的bgsa显然需要更少的迭代，这意味着更少的时间来获得最佳解决方案。能过仿真可知，本发明方法仍优于其他策略，特别与粒子群优化算法pso进行了对比，它具有类似的基于总体搜索来找到最佳解决方案的方法。

附图说明

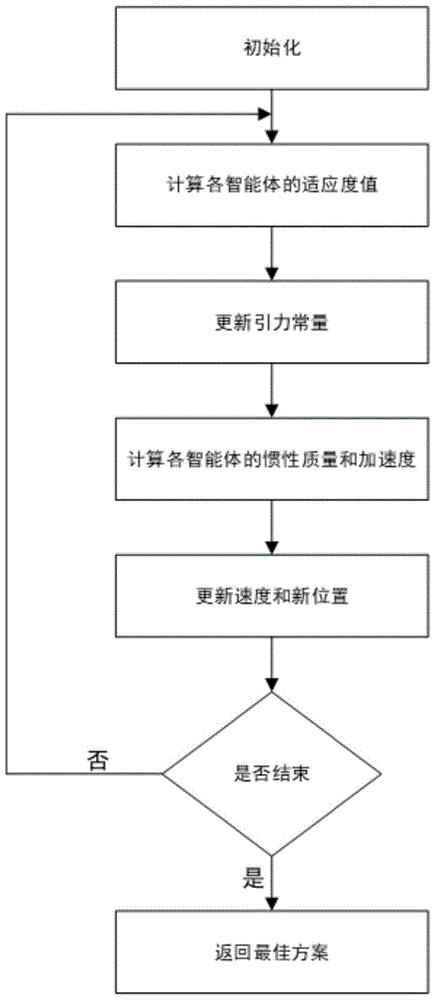
图1为gsa算法流程图；

图2是使用不同的虚拟机放置位置并根据设置表1获得的功耗图；

图3是每个虚拟机放置中活跃服务器的数量图；

图4是使用不同的虚拟机放置并根据设置表2获得的功耗图；

图5是bgsa和pso的能源消耗比较图。

附图中的横纵坐标中的英文在附图说明中已体现，其它英文为现有算法的缩写。

具体实施方式

结合附图1至5对本发明所述的一种基于二进制引力搜索的节能虚拟机放置方法进行如下详尽阐述：

根据研究现状可知，本发明研究的问题属于np问题，首要目标是按照降低能耗标准将虚拟机放置到服务器中，在这种情况下我们使用名为引力搜索算法(gsa)的元启发式方法搜索算法。

gsa基于重力定律，这个算法的研究对象是智能体(agent)，这些智能体的性能是由它们的质量所决定的。按照物理学的相关定律，这些客体会因为引力的作用相互吸引，轻的客体会向更重客体的方向移动，因此具有更高质量的智能体会有更好的解决方案，并且会移动的更慢。在gsa中，每个智能体有四个参数：位置、惯性质量、主动重力质量和被动重力质量。每个智能体的位置与问题的解相对应，它的重力和惯性质量用适应度函数来确定。为了在搜索空间中找到解决方案，算法会调整惯性质量和重力质量。在每一次迭代中，所有的智能体都会被具有最大质量的智能体所吸引。这个质量将在搜索空间中给出一个最优解。类似物理学中牛顿引力和运动定律，gsa中的智能体也满足如下两条定律：

(1)重力定律：智能体之间互相吸引，引力的大小与质量的乘积成正比，与它们之间的距离r成反比.

(2)运动规律：任何智能体的当前速度等于其先前速度分量和速度的变化之和。任何智能体的速度或加速度的变化等于作用在系统上的力除以惯性质量。

图1是gsa算法的流程图。

对于虚拟机放置的问题，我们使用了改进的引力搜索算法，即二进制引力搜索算法(bgsa)，对每一个智能体a，用矩阵ak定义它的位置，

ak是第k个对象的矩阵位置，当将第i个虚拟机分配给第j个服务器时，对应位等于1否则等于0。连续gsa与二进制gsa之间的主要区别是，在二进制算法中，位置更新意味着在“0”和“1”值之间进行切换。质量速度将负责切换位置的对应位。

力、加速度和速度的更新程序可以被认为类似于连续算法。二进制gsa的主要不同是在二进制算法中，位置更新意味着在“0”和“1”之间切换。智能体的速度将负责对应位的切换。通过这样的方式它的目标是以一种当前的方式更新位置位值并用计算出的概率改变根据质量速度。这意味着bgsa更新速度同时并考虑新位置(给定的概率为1或0)。

在这里了解bsga的一些基础知识算法行为：

速度的绝对值显示当前位置应该移动多少，绝对值越小意味着智能体距离它的最佳位置最近，经过有限数量的迭代后，速度的绝对值会收敛到0。

下面阐述本算法涉及的相关概念和对应的计算公式：

考虑一个含有n个智能体的系统，用xi定义第i个智能体的位置，

fori＝1，2，…，n

其中x^di代表第i个智能体在第d个维度的位置。

用f^dij(t)表示在t时刻智能体j对i的力，计算公式为：

其中mpi(t)和maj(t)分别为作用粒子j的惯性质量和被作用粒子i的惯性质量，ε是一个很小的常量，g(t)是在t时刻的引力常数。

引力常数g(t)的计算公式为：

其中g0等于100，a等于20，t是系统迭代的次数。

在引力搜索算法中，为了增加随机特性，假设在第d维上作用在第i个智能体上的总的作用力是其他所有智能体作用力的总和，其大小f^di(t)的定义如下：

其中randj是范围0到1间的随机数，是第d维中第j个智能体作用在第i个智能体上的引力。

根据牛顿第二定理，粒子i在第d维上t时刻的加速度adi(t)的计算方法如下：

其中mi(t)是第i个智能体的惯性质量,它是由智能体的适应度计算出来的(适应度已知)，计算公式为：

mai＝mpi＝mii＝mi，i＝1，2，…，n

其中fiti(t)表示在第t时刻，智能体i的适应度，对于求最大值问题，worst即适应度值的最小值，相应的best即为适应度值的最大值，

在本算法中，对于每一次的迭代过程，智能体都会根据以下公式更新它的速度和位置：对于小|v^di|，更改x^di的概率必须为接近零,且|v^di|大时，x的概率运动必须很高。

我们定义s(v^di(t))为转化x^di成概率函数的函数。s(v^di(t))应该限制在区间[0,1]内，并随着s|v^di(t)|的增加而增加。s(v^di(t))的定义为：

s(v^di(t))＝|tranh(v^di(t))|

一旦s(vdi(t))被计算出,将随下列公式移动

下面介绍算法的实现步骤，主要是基于bgsa算法和虚拟机放置的新定义。

步骤1:初始化，将服务器资源列表定义为向量，大小为m，m是数据中心中的服务器数量；将虚拟机(vm)列表定义为向量，大小为n，n是数据中心中的服务器数；

定义代理数和迭代次数；

步骤2：随机设置每个智能体的位置，确保位置在搜索空间中即可；

步骤3：在每次迭代中，我们计算初始位置的所有智能体的适应度，如果本轮迭代中的适应度高于上一轮迭代的适应度，则更新；

步骤4：对于每个智能体，都根据新的适应度计算质量，引力常数也会随着迭代次数的增加而更新，即随着时间的变化，重力值也会随之变化；用新质量和重力值计算加速度；

步骤5：在搜索空间中移动智能体的位置。

算法1和算法2的伪代码如下所示：

算法1的伪代码如下：

输入：vm列表，服务器列表，

输出：虚拟机放置最佳位置，

1)初始化；

2)确定最大迭代次数；

3)计算适合度；

4)更新适应度；

5计算惯性质量m；

6计算引力常数；

7计算加速度；

8移动代理机的位置；

9结束迭代；

10返回位置。

算法2的伪代码如下：

输入：加速度，速度，当前位置

输出：新位置

1计算新速度；

2计算转化x^di成概率函数的函数s；

3产生要完成的动作；

4对于每一个智能体，执行5；

5寻找改变的比特位；更新比特位；更新位置；

6结束；

7返回新位置。

针对本发明的效果进行如下验证：

为了实现改进的bsga算法，我们使用了在windows764位上运行的matlab版本r2015b，以及配备16g内存的inteli73.4ghz处理器。除比较算法外，算法中所需的所有功能均在matlab中实现。

为了进行准确的比较，我们对所有算法使用相同的虚拟机集，并使用相同数量的物理资源。我们用能耗和静态资源(例如cpu和内存)模拟一组具有不同能耗的异构服务器，当数据中心中的服务器设备不同时，能耗比例也不同。在此模拟中，使用如表1所示的服务器类型。

表1服务器类型

每个模拟中的服务器需要设置成能支持最坏的分配方案的数量。对于虚拟机，我们使用树类型。低，中，高资源需求如表2所示。

表1虚拟机类型

比较算法的仿真结果如图2所示。所有算法都使用相同的服务器设置，并基于表1和2放置了相同的vm组。

对于第一个模拟，我们尝试将虚拟机数量设置为100以下，并比较所有服务器的能耗，我们注意到对于少量虚拟机，由于复杂度低，算法给出的结果非常相似。这给我们一个积极的信号，表明bgsa正在寻找最佳解决方案并按照我们的要求工作。对于数量更多的虚拟机，发散起点和算法给出不同的结果；但是，我们提出的解决方案仍然具有更好的效果，但差异很小。在50个虚拟机下，放置问题很简单，最优解决方案很快就得到了，这就是为什么仿真中使用的所有方法都得到非常相似的结果的原因。随着虚拟机数量的增加，我们的方法对布局问题反应良好，并获得了更好的能量，而其他策略则偏离了最佳策略。

图3显示了针对不同策略放置的每个虚拟机放置后活动的服务器数量。正如预期的那样，对于bgsa，活动服务器的数量很少，这就是能耗降低的原因。

图4显示了表2中vm类型2的相同仿真的结果，我们想探索算法在不同情况下的可能性和性能。与最佳拟合和最差拟合相比，gsa和pso的能耗更高。但是，当vm数量增加时，bgsa也会逐渐提供总体上更好的能耗。

bgsa和pso在定义和工作方式上有相似之处。两种算法都有许多智能体和粒子(用于pso)，它们代表了一个问题的可能解决方案，并且经过多次迭代，全局代理和粒子收敛为最优解。我们针对这两种算法运行了不同的仿真，并更改了迭代参数，并确定了代理或粒子的数量。

确保对于每次仿真，要放置的虚拟机是相同的。因此，从图5我们可以注意到，在bgsa中比pso迭代次数少的最佳选择。bgsa显然需要更少的迭代，这意味着更少的时间来获得最佳解决方案。

对于下一个仿真，希望增加vm的数量并增加设置的多样性，以创建更多异构的系统。我们在表3和4中介绍第二种设置。

表3:服务器设置2

表4:虚拟机设置2

在第二个模拟中，我们尝试使用表3和表4中的设置最多放置300个vm，bgsa给出了能耗的更好结果。在50个虚拟机以下，此数量对于在虚拟机放置之间获得不同结果并不重要。在此仿真中，我们确保vm的数量大于先前的仿真，并且我们注意到我们的方法仍优于其他策略，特别是pso，它具有类似的基于总体搜索来找到最佳解决方案的方法(在这种情况下为粒子pso和bgsa代理)。