边界积分方程中未知变量域积分的三重互易法转化方法与流程

本发明属于计算机辅助工程技术领域，尤其涉及一种边界积分方程中未知变量域积分的三重互易法转化方法。

背景技术：

目前，最接近的现有技术：计算机辅助工程(cae)技术在工程结构设计和分析中发挥着重要的作用，边界积分方程方法或边界元法(bem)为cae分析中重要的数值计算方法之一。采用bem求解工程问题具有计算精度高、降维、减少前处理时间等特点。降维是边界积分方程方法最重要的优势之一，即仅需对问题域的边界进行离散和积分，这将降低模型网格划分难度、减少积分计算时间、降低问题的计算规模。但非齐次问题的边界积分方程中不可避免地会出现域积分，如含有内部热源的热传导问题和有体力的力学问题等，其次，若物理问题的控制方程无解析基本解，或基本解太复杂而不便于使用时，则只能使用该方程不完整算子的基本解，而将原方程左端的一部分移到方程右端，这样也会导致最终得到的边界积分方程中包含未知变量的域积分，如使用拉普拉斯基本解的赫姆霍兹方程、使用拉普拉斯基本解的瞬态热传导问题、使用弹性静力学方程基本解的弹性屈曲问题等，若对出现的域积分采用域内单元的方案，此时需要对问题域进行体网格划分，复杂结构将导致问题域划分体网格困难且耗时，甚至无法完成高质量的域内网格划分，bem的降维优势完全丧失，所以，边界积分方程方法中域积分转化方法的研究十分重要。

现已有几种域积分转化方法被提出，并被成功地应用于稳态热传导、弹性静力等问题中，如双重互易法、三重互易法、径向积分法等。其中双重互易法的计算精度对域内离散点的分布十分敏感，精度不够稳定；双重互易法和径向积分法对于不同的域积分将采用不同的径向基函数插值，径向基函数的选取也将影响最终的计算结果；其中三重互易法具有统一的插值与转化方法，但目前不能应用于转化未知函数的域积分。

综上所述，现有技术存在的问题是：(1)域内插值点的分布以及基函数的选取使得现有的其他域积分转化方法不稳定；(2)三重互易法具有统一的插值与转化方法，但并不能应用于转化未知函数的域积分。

解决上述技术问题的难度：基于现有的三重互易法，提出改进的三重互易方法，得到转化未知变量的域积分的统一格式。

解决上述技术问题的意义：形成一种可以转化已知函数和未知函数域积分的域积分转化方法，使得边界元法再求解非齐次问题以及基本解太复杂的问题时，保持无需划分域内单元、简化前处理的优点，大幅减少复杂结构仿真计算中的前处理时间。

技术实现要素：

针对现有技术存在的问题，本发明提供了一种边界积分方程中未知函数的域积分转化方法。

本发明是这样实现的，一种边界积分方程中未知函数的域积分转化方法，所述边界积分方程中未知函数的域积分转化方法包括以下步骤：

第一步，针对右端含未知变量的偏微分方程，以控制方程的格林函数作为基本解推导得到问题的边界积分方程；

第二步，利用三重互易插值方法，近似得到所述域积分中未知函数的高阶导数；

第三步，利用三重互易法，把含未知函数的域积分转换为含未知函数的边界积分，使得到的边界积分方程只含有边界积分；

第四步，基于边界元法理论进行表面网格划分，并在域内分布插值点，以边界节点作为源点得到边界积分方程，基于网格模型与高斯积分得到矩阵方程；

第五步，以所有的域插值点为源点建立边界积分方程，并得到其矩阵方程，联立以边界节点为源点的矩阵方程，加入边界条件，可求解该问题。

进一步，所述边界积分方程中未知变量域积分的三重互易法转化方法具体包括以下步骤：

以helmholtz方程为例，将未知函数的一次项移动至方程右边，得到右端含有未知变量的拉普拉斯方程：

其中x为一般空间坐标，在边界积分方程中称为场点，u(x)是物理变量，ω代表所考虑的域，γ为已知系数。该方程的基本解或格林函数满足如下方程：

上式的解，即基本解或格林函数表示为：

其中r为源点y到场点x的距离，基本解简记为u*和q*，利用上述基本解和互易定理，得到如下边界积分方程：

其中，γ为所求问题的区域ω的边界。

含有未知函数的域积分为：

式中，y为边界元中的源点，u^*(x，y)是基本解。d代表含未知函数的域积分。

进一步，所述第二步具体包括：

未知域函数u(x)将被b¹(x)近似替换，b¹(x)必须满足以下两个条件：

其中，b²(x)和b³(x)为待定未知函数，m为内部点的个数；式中的未知域函数b²(x)，b³(xm)，和运用边界积分方程来求解；利用边界元理论，将上式转换为边界积分方程，得到如下边界积分方程：

其中，y∈γ，ym∈ω，u^*(j)是更高阶的基本解，其定义如下：

定义边界上有n个节点，在所有内部点处中定位源点y，得到2n+m方程，得到如下的离散化结果：

其中向量的定义如下：

b^j[i]＝b^j(xi),xi∈γ

b^jd[i]＝b^j(xi),xi∈ω；

矩阵的分量如下：

令b²＝0，有；

其中，b¹(x)是未知量，未知的bn¹(x)，bn²(x)和b³(xm)不能被直接求解；

利用改进的三重互易法，将未知向量bn¹，bn²，和b^3d分别用b¹和b^1d表示，有：

b^3d＝t⁰b^1d+τ¹b¹；

其中：

g^-1＝[g]^-1

τ²＝-g^-1g^1d,τ³＝g^-1h¹

τ⁴＝g^-1g²,τ⁵＝g^-1g^2d。

进一步，所述第三步利用三重互易法，把含未知函数的域积分转换为含未知函数的边界积分；

用互易定理将域积分d⁽¹⁾转化为边界积分，具体方法如下：

其中，bn^j(x)是域函数b^j(x)的导数，定义为：

将d⁽¹⁾转化后的方程带入到原边界积分方程中，得到纯边界积分方程：

进一步，所述第四步，基于边界元法理论进行表面网格划分，并在域内分布插值点，以所有的域插值点为源点建立边界积分方程，并得到其矩阵方程；

离散化边界γ转化为边界单元，取所有边界节点为边界积分方程的源点，得到n(边界节点个数)个方程，基于边界单元进行高斯积分，可得到如下线性方程组：

式中，右边的未知向量均用b¹和b^1d表示，此处的b¹和b^1d即为u和ud，然后得到下面的方程：

hu-gq＝τ⁷u+τ⁸ud；

其中：

τ⁶＝[(g²τ⁴-g³)τ²+g²τ⁵-g^3d]

τ⁷＝-γ[g²τ³-h²+τ⁶τ¹]

τ⁸＝-γ[τ⁶t⁰]；

式中，向量u和q，一半元素为已知边界条件，仅含一个未知向量，但是右端新增加了一个未知向量ud，方程不能直接求解。

进一步，所述第五步，以所有的域插值点为源点建立边界积分方程，并得到其矩阵方程，联立以边界节点为源点的矩阵方程，加入边界条件，可求解该问题；具体步骤包括：

以所有的域插值点为源点建立边界积分方程，并基于边界单元与单元积分，得到其矩阵方程：

整理得到：

其中：

联立方程：

利用自由度凝集，最终得到矩阵方程：

h′u-g′q＝0；

其中：

求解方程h′u-g′q＝0后，将得到的u和q带入下式：

得到域变量ud。

本发明的另一目的在于提供一种所述边界积分方程中未知变量域积分的三重互易法转化方法在计算机辅助工程中的应用。

综上所述，本发明的优点及积极效果为：本发明将未知函数域积分转换成一定边界条件下的未知函数边界积分方法，通过域内插值等式和三元互易方法，得到未知函数变量间关系，可以很好的解决含有未知函数的域积分问题，以实现问题域内无需划分单元而只需分布插值点，简化了数值仿真中的前处理难度，大幅减少了仿真计算的前处理时间。

附图说明

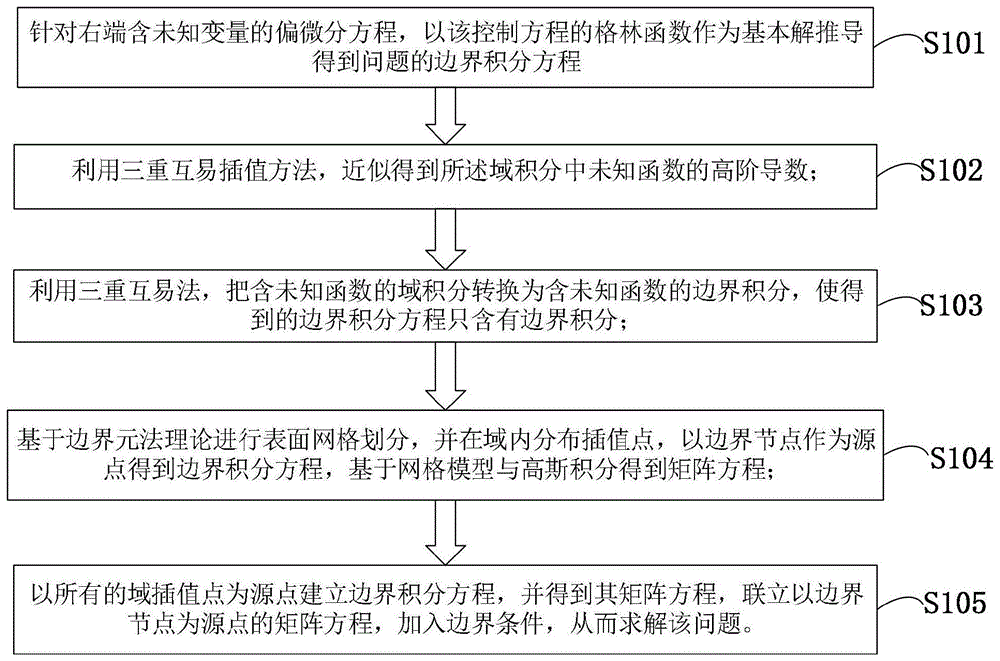
图1是本发明实施例提供的边界积分方程中未知变量域积分的三重互易法转化方法流程图。

图2是本发明实施例提供的薄壁圆柱壳的几何与边界元模型示意图；

图中：(a)薄壁圆柱壳的几何与边界元模型；(b)边界元模型。

图3是本发明实施例提供的u(x)在薄圆柱壳上的分布示意图；

图中：(a)u(x)的精确分布；(b)用三重互易边界元法计算u(x)的数值结果。

图4是本发明实施例提供的圆线上u(x)的比较r＝10.2，z＝1.6示意图。

图5是本发明实施例提供的q(x)在薄圆柱壳上的分布示意图；

图中：(a)q(x)的精确分布；(b)用三重互易边界元法计算q(x)的数值结果。

图6是本发明实施例提供的圆线上q(x)的比较r＝10.2，z＝1.6示意图。

图7是本发明实施例提供的球面块中三重互易边界元法的相对误差示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

针对现有技术存在的问题，本发明提供了一种边界积分方程中未知变量域积分的三重互易法转化方法，下面结合附图对本发明作详细的描述。

工程问题的数值仿真常需要将问题域划分为体网格，复杂结构将导致问题域划分体网格困难且耗时，如采用边界积分方程方法分析helmholtz问题、瞬态热传导问题，其边界积分方程中将含未知函数域积分，需要对问题域进行体网格划分。

如图1所示，本发明实施例提供边界积分方程中未知函数的域积分转化方法包括以下步骤：

s101：针对右端含未知变量的偏微分方程，以控制方程的格林函数作为基本解推导得到问题的边界积分方程；

s102：利用三重互易插值方法，近似得到所述域积分中未知函数的高阶导数；

s103：利用三重互易法，把含未知函数的域积分转换为含未知函数的边界积分，使得到的边界积分方程只含有边界积分；

s104：基于边界元法理论进行表面网格划分，并在域内分布插值点，以边界节点作为源点得到边界积分方程，基于网格模型与高斯积分得到矩阵方程；

s105：以所有的域插值点为源点建立边界积分方程，并得到其矩阵方程，联立以边界节点为源点的矩阵方程，加入边界条件，可求解该问题。

本发明实施例提供的一种边界积分方程中未知变量域积分的三重互易法转化方法具体包括以下步骤：

以helmholtz方程为例，将未知函数的一次项移动至方程右边，得到右端含有未知变量的拉普拉斯方程：

其中，x为一般空间坐标，在边界积分方程中称为场点，u(x)是物理变量，ω代表所考虑的域，γ为已知系数。该方程的基本解或格林函数满足如下方程：

上式的解，即基本解或格林函数表示为：

其中，r为源点y到场点x的距离，基本解简记为u*和q*，利用上述基本解和互易定理，得到如下边界积分方程：

其中，γ为所求问题的区域ω的边界。

含有未知函数的域积分为：

式中，y为边界元中的源点，u^*(x，y)是基本解，d代表含未知函数的域积分。

本发明实施例提供的一种边界积分方程中未知变量域积分的三重互易法转化方法s102具体包括：

未知域函数u(x)将被b¹(x)近似替换，b¹(x)必须满足以下两个条件：

其中，b²(x)和b³(x)为待定未知函数，m为内部点的个数；式中的未知域函数b²(x)，b³(xm)，和运用边界积分方程来求解；利用边界元理论，将上式转换为边界积分方程，得到如下边界积分方程：

其中，y∈γ，ym∈ω，u^*(j)是更高阶的基本解，其定义如下：

定义边界上有n个节点，在所有内部点处中定位源点y，得到2n+m方程，得到如下的离散化结果：

其中向量的定义如下：

b^j[i]＝b^j(xi),xi∈γ

b^jd[i]＝b^j(xi),xi∈ω；

矩阵的分量如下：

令b²＝0，有；

其中，b¹(x)是未知量，未知的bn¹(x)，bn²(x)和b³(xm)不能被直接求解；

利用改进的三重互易法，将未知向量bn¹，bn²，和b^3d分别用b¹和b^1d表示，有：

b^3d＝t⁰b^1d+τ¹b¹；

其中：

g^-1＝[g]^-1

τ²＝-g^-1g^1d,τ³＝g^-1h¹

τ⁴＝g^-1g²,τ⁵＝g^-1g^2d。

本发明实施例提供的一种边界积分方程中未知变量域积分的三重互易法转化方法s103中，利用三重互易法，把含未知函数的域积分转换为含未知函数的边界积分；

用互易定理将域积分d⁽¹⁾转化为边界积分，具体方法如下：

其中，bn^j(x)是域函数b^j(x)的导数，定义为：

将d⁽¹⁾转化后的方程带入到原边界积分方程中，得到纯边界积分方程：

本发明实施例提供的一种边界积分方程中未知变量域积分的三重互易法转化方法s104中，基于边界元法理论进行表面网格划分，并在域内分布插值点，以所有的域插值点为源点建立边界积分方程，并得到其矩阵方程；

离散化边界γ转化为边界单元，取所有边界节点为边界积分方程的源点，得到n(边界节点个数)个方程，基于边界单元进行高斯积分，可得到如下线性方程组：

式中，右边的未知向量均用b¹和b^1d表示，此处的b¹和b^1d即为u和ud，然后得到下面的方程：

hu-gq＝τ⁷u+τ⁸ud；

其中：

τ⁶＝[(g²τ⁴-g³)τ²+g²τ⁵-g^3d]

τ⁷＝-γ[g²τ³-h²+τ⁶τ¹]

τ⁸＝-γ[τ⁶t⁰]；

式中，向量u和q，一半元素为已知边界条件，仅含一个未知向量，但是右端新增加了一个未知向量ud，方程不能直接求解。

本发明提供的一种边界积分方程中未知变量域积分的三重互易法转化方法s105中，以所有的域插值点为源点建立边界积分方程，并得到其矩阵方程，联立以边界节点为源点的矩阵方程，加入边界条件，可求解该问题；具体步骤包括：

以所有的域插值点为源点建立边界积分方程，并基于边界单元与单元积分，得到其矩阵方程：

整理得到：

其中：

联立方程：

利用自由度凝集，最终得到矩阵方程：

h′u-g′q＝0；

其中：

求解方程h′u-g′q＝0后，将得到的u和q带入下式：

得到域变量ud。

下面结合具体实施例对本发明的技术效果作详细的描述。

实施例

为了验证三重互易法转化未知函数的域积分的有效性，计算如下实施例：

薄圆柱壳中的正弦函数型分布，在这个例子中，考虑了四分之一具有正弦函数型分布的薄圆柱壳。其几何尺寸如图2(a)所示。解析场如下式：

u(x,y,z)＝sinx·siny·sinz

选择了两种不同的边界条件：

第一种边界条件是圆柱面r＝10.2上施加纽曼边界条件q(x)，其他面施加狄里克莱边界条件u(x)。

在这个仿真中，边界被离散成980个二次四边形单元，有3358个节点，如图2(b)所示。以及域内均匀分布的2730个插值点。

图3给出了通过三重互易-边界元法求得的u(x)的分布与精确解的比较。三重互易-边界元法结果的分布云图与精确结果吻合较好。

图4给出了弧曲线r＝10.2，z＝1.6上节点的u(x)，包括基于三重互易-边界元法的数值解与精确解。比较结果表明，三重互易-边界元法的计算结果与精确解吻合较好，说明三重互易-边界元法的精度较高。

第二种边界条件：在圆柱面r＝10.2上施加狄里克莱边界条件u(x)，其它面施加纽曼边界条件q(x)。

图5分别给出了精确解和三重互易-边界元法的q(x)结果的分布。三重互易-边界元法的结果的q(x)分布与精确解的q(x)分布吻合较好。同时，三重互易-边界元法的结果的q(x)分布云图与精确解的q(x)分布云图非常接近，三重互易-边界元法的结果的的最大值和最小值与精确解的误差都很小。

图6示出了r＝10.2，z＝1.6线上节点的具体数值解与精确解之间的q(x)的分布的比较。图6中的两条线之间的差别很小，同样证明三重互易-边界元法的精度很高。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。