一种基于效用函数的发电商竞价方法与流程

本发明涉及电力市场技术领域，尤其涉及一种基于效用函数的发电商竞价方法，主要适用于提高发电商竞价效率。

背景技术：

近年来，我国电力市场改革不断深入，发电侧打破传统垂直垄断的市场结构，逐步建立了“厂网分开，竞价上网”的机制，在这种局势下，发电商的利润与其报价密切相关，如何制定最优的报价策略以实现利润最大化成为发电企业急需解决的问题，对发电企业市场行为进行研究，分析市场竞价交易最优策略，以期实现电力市场的资源合理配置，激励发电商进一步降低发电成本成为当前的研究热点。

在电力市场中，发电商的报价策略主要有根据报价经验指导自身实现最优报价和采取博弈论寻求纳什均衡解两种方法，由于根据报价经验指导自身实现最优报价方法主观性较强，并且在初期开展电力市场的地区缺少报价经验数据，因此，近年来，利用博弈论进行报价策略研究成为趋势。但在现有研究中，模型普遍存在数据难以获得，算法过程过于复杂，容易出现无纳什均衡解的情况。

技术实现要素：

本发明的目的在于提供一种基于效用函数的发电商竞价方法，该方法可以为发电商参与电力市场交易提供有益指导，有效提高发电商竞价效率。

为实现以上目的，本发明的技术解决方案是：一种基于效用函数的发电商竞价方法，该方法包括以下步骤：

a、建立发电商报价变量函数；

b、建立贝叶斯博弈模型，引入效用函数，计算在不同报价情况下发电商的收益效用函数；

构建收益效用函数为：

上式中，ui为发电商i的收益；fi为发电商i的报价；为发电商i报价类型变量；fj为发电商j的报价；pi为发电商i的供电量或发电出力；n为竞争对手企业数量；ε为边际上网电量比，0＜ε＜1；

c、求解一阶最优条件，获得纳什均衡解即为发电商最优报价。

步骤a中，发电商i报价变量函数为：

上式中，αi为发电商i报价系数1；βi为发电商i报价系数2；ci为发电商i的成本；p1为市场历史成交价格平均值；cm为市场平均发电成本；k为市场平均收益与发电商i的成本ci的比值。

步骤b中，边际上网电量比ε的具体计算公式为：

上式中，q为市场总需求电量；pm为竞争对手企业的供电量或发电出力。

步骤c具体包括以下步骤：

对于发电商i报价类型变量发电商i的最优报价使得下式成立：

假设服从上的均匀分布，则服从上的均匀分布，得出：

上式中，为发电商i报价类型变量下限；为发电商i报价类型变量上限；αj为发电商j报价系数1；βj为发电商j报价系数2；

所以：

上式对fi求偏导得：

使偏导为0，得出：

又根据可得：

同理可得：

解上述两个方程式，可得：

所以，发电商i最优报价的表达式为：

与现有技术相比，本发明的有益效果为：

本发明一种基于效用函数的发电商竞价方法中建立了引入效用函数的发电商最优竞价贝叶斯博弈模型，以发电商收益效用最大为目标，对模型进行了求解，以此提出了发电商最优竞价策略，可以在已知信息较少的情况下，为发电商参与市场交易提供有益参考，提高发电商竞价效率。

附图说明

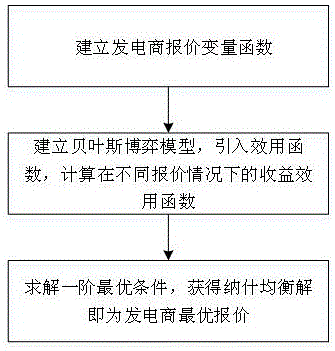
图1是本发明一种基于效用函数的发电商竞价方法的流程图。

具体实施方式

以下结合附图说明和具体实施方式对本发明作进一步详细的说明。

参见图1，一种基于效用函数的发电商竞价方法，该方法包括以下步骤：

a、建立发电商报价变量函数；

b、建立贝叶斯博弈模型，引入效用函数，计算在不同报价情况下发电商的收益效用函数；

构建收益效用函数为：

上式中，ui为发电商i的收益；fi为发电商i的报价；为发电商i报价类型变量；fj为发电商j的报价；pi为发电商i的供电量或发电出力；n为竞争对手企业数量；ε为边际上网电量比，0＜ε＜1；

c、求解一阶最优条件，获得纳什均衡解即为发电商最优报价。

步骤a中，发电商i报价变量函数为：

上式中，αi为发电商i报价系数1；βi为发电商i报价系数2；ci为发电商i的成本；p1为市场历史成交价格平均值；cm为市场平均发电成本；k为市场平均收益与发电商i的成本ci的比值。

步骤b中，边际上网电量比ε的具体计算公式为：

上式中，q为市场总需求电量；pm为竞争对手企业的供电量或发电出力。

步骤c具体包括以下步骤：

对于发电商i报价类型变量发电商i的最优报价使得下式成立：

假设服从上的均匀分布，则服从上的均匀分布，得出：

上式中，为发电商i报价类型变量下限；为发电商i报价类型变量上限；αj为发电商j报价系数1；βj为发电商j报价系数2；

所以：

上式对fi求偏导得：

使偏导为0，得出：

又根据可得：

同理可得：

解上述两个方程式，可得：

所以，发电商i最优报价的表达式为：

本发明的原理说明如下：

由于在当前电力市场交易背景下，用成本作为类型空间只能反映市场的成本，不能反映市场价格平均水平，而现行的市场上企业报价受市场平均报价影响更多，因此，引入报价类型变量其为发电商成本和市场平均收益之和，市场平均收益由市场历史成交价格平均值p1和市场平均发电成本cm作差求得。

决策者在进行决策时，其决策结果往往会受到主观意愿的影响，然而主观意愿比较抽象并且难以用数学方式进行计算，为了便于进行定量分析，引入效用函数来描述决策者的收益价值；效用函数认为决策者更为关注财富的相对变化，而不是最终财富数值的大小，通过效用函数可以量化财富对决策者的价值。

收益效用函数中三种情况分别为：

(1)发电商i报价低于其他发电商j报价，此时，发电商i所有申报电量都竞标成功；

(2)发电商i报价与其他发电商j报价相同，这种情况下为随机中标，发电商i和发电商j中标概率相同，若有n家企业出价相同，则中标概率均为1/n，其期望收益为全部电量上网的1/n倍；

(3)发电商i报价高于其他发电商j报价，此时，发电商i只有部分竞标电量能够上网。

实施例：

参见图1，一种基于效用函数的发电商竞价方法，该方法包括以下步骤：

a、建立发电商报价变量函数；

发电商i报价变量函数为：

上式中，αi为发电商i报价系数1；βi为发电商i报价系数2；ci为发电商i的成本；p1为市场历史成交价格平均值；cm为市场平均发电成本；k为市场平均收益与发电商i的成本ci的比值；

b、建立贝叶斯博弈模型，引入效用函数，计算在不同报价情况下发电商的收益效用函数；

由于报价受市场平均报价影响更多，所以以作为收益参考值，则构建收益效用函数为：

上式中，ui为发电商i的收益；fi为发电商i的报价；为发电商i报价类型变量；fj为发电商j的报价；pi为发电商i的供电量或发电出力；n为竞争对手企业数量；ε为边际上网电量比，0＜ε＜1；εpi为发电商i最后上网时的上网电量；

边际上网电量比ε的具体计算公式为：

上式中，q为市场总需求电量；pm为竞争对手企业的供电量或发电出力；

c、求解一阶最优条件，获得纳什均衡解即为发电商最优报价；

具体包括以下步骤：

对于发电商i报价类型变量发电商i的最优报价使得下式成立：

假设服从上的均匀分布，则服从上的均匀分布，在连续分布的情况下，发电商不可能出价相同，则p(fi＝fj)＝0，得出：

上式中，为发电商i报价类型变量下限；为发电商i报价类型变量上限；αj为发电商j报价系数1；βj为发电商j报价系数2；

所以：

上式对fi求偏导得：

使偏导为0，得出：

又根据可得：

同理可得：

解上述两个方程式，可得：

所以，发电商i最优报价的表达式为：

结合某时段电力市场交易进行进一步说明。

假设在某电力市场交易中，共有5家发电商进行竞价交易，均以其最大可供电量参与竞争；该交易采取统一价格出清成交模型，该地区单位标准煤的价格是710元/吨，可以认为此次交易中发电商的发电标准煤耗率水平无明显变化，估计发电标准煤耗率的值处于区间[290，310](克/千瓦时)，则发电企业a、b、c、d、e的单位发电成本范围为[0.2059，0.2201](元/千瓦时)，k为市场平均收益与发电商ci的比值，由市场历史数据求得k＝0.9，则的范围为[0.3912,0.4182](元/千瓦时)，所以元/千瓦时，元/千瓦时。

这一时段电量需求q＝2600mwh，收集到各个企业发电标准煤耗率信息，如表1所示。

以企业c为例，当c的报价比a、b、d、e四家企业都高，则c最后上网，成为边际机组，能够上网的电量为市场总需求减去a、b、d、e四家企业的供电量(2600-300-500-700-900)＝200mwh，则ε为能够上网电量与企业c最大供电量之比，ε＝200/600＝0.33，则企业c的最优报价为：

元/千瓦时

由调研可得该地区不同发电企业交易数据及计算得出的最优报价如表1所示，表中ε为报价预测时的边际上网电量比。

表1不同企业数据及最优报价

根据表1所示算例分析结果，可以得到发电商最优报价与发电成本成正相关；比较企业a和企业b，其边际上网电量比ε相同，企业a的发电成本高于企业b，由于成本较高，为确保利润，企业a的报价也是高于企业b的，若发电商的成本较高，但是报价较低的话，则单位利润较少，无法实现利润最大化的最优竞价策略目标。

根据算例分析结果，还可以发现发电商最优报价与边际上网电量比ε成正相关，由于边际上网电量比是由竞标电量决定的，因此，大用户的最优报价与竞标电量成正相关；比较企业b、c、d三家发电商的发电成本相同，申报的电量越多，其最优报价越高，这是因为当企业的申报电量越多，代表其市场份额占比越大，拥有较高的市场影响力，其报价可以一定程度上影响最终成交价格，此时，企业可以通过报高价实现利润最大化；当发电商的竞标电量较少，若报价较高，可能导致无法中标或中标电量较少，为了确保中标电量，发电商会倾向于报低价。

尽管本发明的内容已经通过上述优选实施例作了详细介绍，但应当认为到上述的描述不应被认为是对本发明的限制。任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应由所附的权利要求来限定。