一种计算薄煤层含气量的方法与流程

本发明涉及煤层气勘探与开发领域，特别涉及一种计算薄煤层含气量的方法。

背景技术：

煤层气作为重要的非常规洁净能源，对煤储层含气量的准确预测在煤矿安全生产和煤层气资源勘探开发评价中都具有重要意义。几十年来，前人对煤层含气量的定量预测做了大量研究。其中，最准确的是煤心解吸测试，但成本较高且测试层位有限，往往不能满足勘探开发评价的需求，而利用测井及物理参数进行的含气量间接评价方法实用、低成本且有较高的分辨率，可以弥补取心及煤心分析资料缺少等方面的不足，应用较广。常用的间接评价方法有回归分析法、含气量梯度法、基于煤层气等温吸附理论提出的各种经验公式法及包括bp神经网络、最优化、灰色系统理论等非线性预测法等。

回归分析法分为单一因素和多因素回归法，最常用的单一因素就是利用含气量和密度测井值(或深度、灰分)的统计关系来预测含气量，由于煤层含气量是多种因素综合影响的结果，考虑到单一因素的回归关系有一定的片面性，也可利用测井值、煤质及其他物理参数与含气量建立多因素线性回归模型来预测。

含气量梯度法是同一煤层中增加单位深度，含气量相应增加，适用于同一构造单元中的深部外推预测，或地质条件相似的预测，但精度较低。

等温吸附法即是用兰式方程来求取不同温度、压力下的含气量，通过研究表明，煤对甲烷的吸附能力与温度和压力有关，但在实际研究中，兰式方程计算含气量均为理论最大吸附量，高于实际解吸量，需要多方面的校正，但目前兰氏方程的多种变形校正公式大多较为繁琐，需要的参数类型较多，应用上具有局限性。

非线性预测法即是利用数学方法来表达影响煤层含气量的多种复杂因素之间的非线性关系，这些关系甚至是随机的、模糊的，常用的算法包括bp神经网络、灰色系统理论、支持向量机等，此类方法准确性较高，但建模所需的数据体量大，模型适用范围小。

另外，上述常用的间接评价方法在中厚及以上煤层有较好的应用效果，但对于厚度小于1m的薄煤层，甚至是不到50cm的极薄煤层，对其含气量的定量预测效果则不理想，尤其是薄煤层与砂泥岩交互沉积的复杂地层，相对于薄煤层而言，因很多测井曲线纵向分辨率低，曲线特征受围岩影响较大，对薄层的响应特征不敏感，严重影响了薄煤层含气量预测的准确度。目前薄煤层的煤层气资源潜力在国内外都越来越受到关注，因此提高薄煤层含气量的定量预测准确性具有较大意义。

技术实现要素：

本发明创造所要解决的技术问题是提供一种计算薄煤层含气量的简单方法，为更准确的计算薄煤层的含气量，为煤层气勘探开发评价提供可靠的技术支持。

为了解决而上述问题，本发明提供了一种计算薄煤层含气量的简单方法，包括：

1)采集待测煤层的基础数据和多个煤心的基础数据；

2)根据步骤1)中每个煤心的基础数据，计算每个煤心样品的临界解吸压力pcd；

3)利用岩性敏感性好的测井补偿密度曲线和自然伽马曲线表征灰分aad；

4)利用步骤3)计算的灰分和校正后的埋深表征兰氏体积、兰氏压力和临界解吸压力；

5)根据步骤3)和步骤4)得到的灰分、兰氏体积、兰氏压力及临界解吸压力，代入如下方程，求取地区经验系数，计算目的层薄煤层现今的含气量：

vgas＝a×(1-aad)×(vl×pcd)/(pcd+pl)+b

式中，a、b为待定系数；

vgas为计算的吨煤含气量，单位为m³/t；

aad为灰分，单位为％；

pcd为临界解吸压力，单位为mpa；

pl为兰氏压力，单位为mpa；

vl为兰氏体积，单位为m³/t。

其中，所述步骤1)中，煤心处的基础数据包括含气量g、工业组分、兰氏体积vl和兰氏压力pl数据；所述待测煤层的基础数据包括常规测井曲线，所述常规测井曲线包括补偿密度测井曲线den和自然伽马测井曲线gr。

其中，所述步骤1)中，煤心处的基础数据的获取方法包括煤层含气量测定、工业组分测定和等温吸附试验。

其中，所述煤层含气量测定按照《煤层气含量测定方法gb/t19559-2008》标准规定的流程对煤心样品进行实验分析；

所述工业组分测定按照《煤的工业分析方法gb/t212-2008》标准规定的流程对煤心样品进行实验分析；

所述等温吸附试验《煤的高压等温吸附试验方法gb/t19560-2008》标准规定的流程对煤心样品进行实验分析。

其中，所述步骤1)中还包括将煤心深度校正到测井深度。

其中，所述步骤2)中所述煤心样品的临界解吸压力pcd用如下公式计算：

pcd＝g×pl/(vl-g)

式中，g为煤心实测含气量，m³/t；pcd为临界解吸压力，mpa；vl为兰氏体积，m³/t；pl为兰氏压力，mpa。

其中，所述步骤3)中所述的灰分按照如下公式进行计算：

aad＝a1×den+b1×gr+c1

式中，a1、b1、c1为待定系数；

aad为灰分，％；den为补偿密度测井曲线，g/cm³；gr为自然伽马测井曲线，api。

其中，步骤4)所述的兰氏体积vl、兰氏压力pl和临界解吸压力pcd利用如下公式表征：

vl＝a2×aad+b2

pl＝c2×h+d2

pcd＝e2×h+f2

式中，a2、b2、c2、d2、e2、f2为待定系数；

h为测井校正后的煤层埋深，单位为m；

aad为灰分，单位为％；

vl为兰氏体积，单位为m³/t；

pcd为临界解吸压力，单位为mpa；

pl为兰氏压力，单位为mpa。

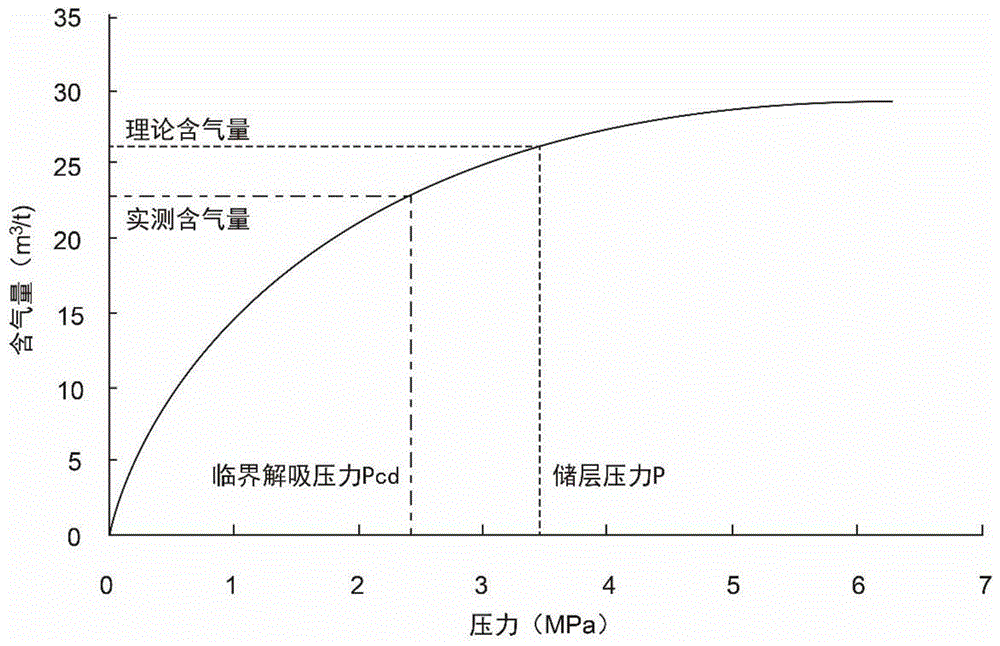
本发明的有益效果在于：本发明是在等温吸附理论模型的基础上，对兰氏方程进行了改进，将储层压力替换成临界解吸压力，并加入了灰分和地区经验系数的校正量，使其更接近实际测定的含气量值，也更适用于区域性煤层含气量的定量估算。经典兰氏方程计算得到的是原始储层压力下的理论吸附量(图1)，而煤心样品实测的含气量是样品所能解吸出来的全部气量，小于理论吸附量；临界解吸压力是使吸附在煤层微孔隙表面的气体开始解吸时的压力，在等温吸附曲线上，实测含气量与临界解吸压力对应的含气量更加匹配。同时，本发明的方法充分考虑薄煤层与砂泥岩互层沉积的地层条件，尽可能减少常规测井曲线在薄煤层数值失真对含气量评价带来的影响，优选纵向分辨率较高的补偿密度和自然伽马测井曲线以及受围岩岩性影响小的地层深度来表征公式参数，建立含气量模型，通过验证，含气量预测准确性较高。另外，本发明的方法在保证地质意义合理和计算准确性的前提下，力求公式形式及参数精简，使其达到更宽更广的应用范围。本发明的方法是对薄煤层含气量定量计算方法的有益补充，同时也适用于中厚及以上煤层厚度条件，且使用的均是常规测井曲线和常用属性参数，具有较广泛的适用价值，为煤层气勘探开发提供了可靠的技术方法。

附图说明

图1等温吸附曲线及临界解吸压力图解；

图2本发明实施例计算薄煤层含气量的方法流程图；

图3灰分与补偿密度交会图；

图4兰氏体积与灰分交会图；

图5兰氏压力与深度交会图；

图6临界解吸压力与深度交会图；

图7本发明计算煤层含气量与实测含气量对比交会图；

图8本发明计算d井煤层含气量与实测含气量对比图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明实施方式进一步地详细描述。

参见图2，本发明实施例提供了一种确定薄煤层含气量的方法，按照如下步骤进行：

步骤一，均匀选取澳大利亚博文盆地区块10口岩心井25个岩心样品，按照《煤层气含量测定方法gb/t19559-2008》、《煤的工业分析方法gb/t212-2008》和《煤的高压等温吸附试验方法gb/t19560-2008》标准规定的流程对煤心样品进行实验分析，包括含气量、工业组分和等温吸附试验，获取实测含气量g、灰分aad、兰氏体积vl、兰式压力pl，具体数据如表1所示；通过进行常规测井作业，获取补偿密度den、自然伽马gr测井曲线，具体数据如表1所示，并将煤心样品深度校正到测井深度。

表1煤心实验测定结果及对应的测井曲线值

步骤二，根据步骤一获取的实测含气量g、兰式体积vl和兰式压力pl计算区块范围的煤层临界解吸压力，按照以下公式进行计算：

pcd＝g×pl/(vl-g)

式中，g为煤心实测含气量，m³/t；pcd为临界解吸压力，mpa；vl为兰氏体积，m³/t；pl为兰氏压力，mpa。

步骤三，如表2所示，常规测井曲线中，补偿密度den和自然伽马gr测井曲线的纵向分辨率较好，对岩性敏感性较强，适用于薄煤层的属性建模；灰分与补偿密度及自然伽马均具有很强的相关性，图3是灰分与补偿密度测井曲线的交会图，显著相关，则利用补偿密度den测井曲线和自然伽马gr测井曲线表征灰分，具体按照如下公式计算：

aad＝a1×den+b1×gr+c1

式中，a1、b1、c1为待定系数；

aad为灰分，％；den为补偿密度曲线，g/cm³；gr为自然伽马曲线，api。

通过多元线性回归运算得到待定系数，a1＝55.129、b1＝0.11、c1＝-60.595，r²是0.8，显著性很好。

表2常规测井系列纵向分辨率及岩性敏感性

步骤四，本发明是在等温吸附法的基础上进行公式及参数的改进，来提高薄煤层含气量的计算精度，即该发明是建立在兰式方程v/vl＝p/(p+pl)的基础上，需要用参数表征兰式体积vl、兰式压力pl和临界解吸压力pcd；灰分对煤的吸附性有负相关影响，如图4所示，兰氏体积随灰分的增大而减小；煤层埋深是兰式压力和临界解吸压力的主要影响因素，如图5、6所示，煤层埋深与两者均具有显著的正相关性，因此本发明利用步骤三计算的灰分和受围岩岩性影响小的煤层埋深来表征兰氏体积、兰氏压力和临界解吸压力，适用于薄煤层的地层条件，可提高计算精度，且所需参数种类少，表征公式形式简单，易于操作和推广，具体按照如下公式计算：

vl＝a2×aad+b2

pl＝c2×h+d2

pcd＝e2×h+f2

式中，a2、b12、c2、d2、e2、f2为待定系数；

h为测井校正后的煤层埋深，m。

通过多元线性回归运算得到待定系数，a2＝0.244、b2＝26.678、c2＝0.003、d2＝0.384、e2＝0.011、f2＝-4.986，r²分别是0.925、0.862和0.814，显著性很好。

步骤五，本发明在经典兰式方程的基础上，将储层压力替换为临界解吸压力，并加入了灰分和地区经验系数的校正量，使其更接近实际测定的含气量值，也有更广泛的区域适用性；将以上步骤获取的各个参数代入改进后的兰氏方程，求取地区经验系数，构建目的层煤层含气量的计算模型，具体按照如下公式计算：

vgas＝a×(1-aad)×(vl×pcd)/(pcd+pl)+b

式中，a、b为待定系数；

vgas为计算的吨煤含气量，单位为m³/t。

通过多元线性回归运算得到待定系数，a＝0.6502、b＝5.6904，r²是0.723

计算的含气量值如表1所示，精度较高，图7是实施例中计算的含气量与煤心实测含气量的对比图，点数基本对称分布于45°线附近，再如图8所示，利用本发明计算d井的含气量曲线与煤心实测含气量样品点吻合得很好，均说明建立的含气量计算模型较为准确。

尽管上面已经示出和描述了本发明的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本发明的限制，本领域的普通技术人员在本发明的范围内对上述实施例进行变化、修改、替换和变型，均落入本发明的保护范围。