适用于低频振荡与次同步振荡辨识的Prony分析方法与流程

本发明涉及电力系统低频振荡和次同步振荡的监测与分析领域，具体而言涉及一种适用于低频振荡与次同步振荡辨识的prony分析方法。

背景技术：

近年来，随着我国跨大区联网进程的加快，特高压输电网络的推进，长距离送电功率的增加，以及远距离交流输电系统中使用串联电容补偿来增大电网的输电能力，这些举措都可能引发电力系统的低频振荡或者次同步振荡。目前，这两种振荡问题已是破坏电力系统安全稳定运行的重要因素之一。非线性时变是大规模复杂电力系统的一种重要特征，对电网中的低频振荡的诱发机理进行探究并且可以在含有噪声的条件下对其进行迅速高效的辨识，是大区域电网能够安全运行以及有效控制的关键因素之一。如今，基于相量测量单元(pmu)的电力系统广域测量系统(wams)在全球大型互联电网的分析与及时监测中被普遍使用着，pmu作为wams主站的数据源，同时也为多种分析算法直接从测量数据中辨识低频振荡模式参数提供了可能。电力系统次同步振荡对整个发电机组和电网的稳定运行有很大危害，当次同步振荡频率与发电机组扭振的固有频率符合特殊的互补条件时可导致发电机组转子轴系扭振快速增大甚至引发机组轴系毁坏事件。对实时系统中的次同步振荡进行及时在线预警并实施有效的抑制措施，对保证整个电网的安全稳定、正常运行都是十分必要的。

利用有效的算法对实测信号进行分析，可确定系统振荡的各个模态及相应参数，从而研究系统振荡的相关问题。从电网中采集到有效的电气量信息，通过合适的辨识算法分析得到系统的振荡频率等参数，是目前在线监测及预警的主要手段。其中prony算法是低频振荡和次同步振荡模态参数辨识中较为常用的辨识方法，该算法通过计算可以直接从信号中提取出振荡的各个模态。但是该算法对噪声非常敏感，容易受到噪声干扰，动态过程的非平稳性难以体现；算法的复矩阵方程组求解困难，存在计算量大的问题，导致灵敏度较大；且传统定阶方法的需要人为选取阈值，阈值的上下浮动对准确定阶会带来误差。因此有必要对prony算法作改进，使算法在运用时能够更加高效、便捷。

技术实现要素：

鉴于现有的低频振荡与次同步振荡辨识中采用的prony算法计算阶数确定的困难以及计算量大的缺陷，本发明的目的在于提供一种适用于低频振荡与次同步振荡辨识的prony分析方法，首先采用基于奇异值分解的方法自动定阶，确定计算阶数求得特征值后采用bp神经网络求解矩阵方程，实现准确定阶和快速求解，从而提高辨识准确度和效率。

本发明的上述目的通过独立权利要求的技术特征实现，从属权利要求以另选或有利的方式发展独立权利要求的技术特征。

为实现上述目的，本发明的第一方面提出一种适用于低频振荡与次同步振荡辨识的prony分析方法，包括：

步骤1、基于实测数据，构建出扩展阶的样本矩阵；

步骤2、采用基于奇异值分解的方法来确定样本矩阵的有效秩，即prony算法的计算阶数；

步骤3、求解特征多项式，根据求得的特征根构建新的矩阵方程；

步骤4、采用基于bp神经网络的方法进行迭代求解前述构造的矩阵方程；

步骤5、基于前述求解得到的特征根与矩阵方程的解计算prony参数：幅值、衰减因子、频率、初相。

本发明以上方案提出的适用于低频振荡与次同步振荡辨识的prony分析方法，对prony算法进行改进，在求解特征值之前确定计算阶数，并使用bp神经网络替代传统prony算法的广义逆求解过程。

由以上本发明的技术方案可知，与现有技术相比，本发明的显著优点在于：

1、设计了一种根据奇异值的特点对prony算法进行定阶的方法，该方法可以避免归一化比值和归一化奇异值法中的阈值选取，实现自动准确定阶；

2、利用bp神经网络对prony算法的复矩阵进行求解，利用神经网络训练权值避免高维复矩阵的求逆计算，提高了计算速度。

应当理解，前述构思以及在下面更加详细地描述的额外构思的所有组合只要在这样的构思不相互矛盾的情况下都可以被视为本公开的发明主题的一部分。另外，所要求保护的主题的所有组合都被视为本公开的发明主题的一部分。

结合附图从下面的描述中可以更加全面地理解本发明教导的前述和其他方面、实施例和特征。本发明的其他附加方面例如示例性实施方式的特征和/或有益效果将在下面的描述中显见，或通过根据本发明教导的具体实施方式的实践中得知。

附图说明

附图不意在按比例绘制。在附图中，在各个图中示出的每个相同或近似相同的组成部分可以用相同的标号表示。为了清晰起见，在每个图中，并非每个组成部分均被标记。现在，将通过例子并参考附图来描述本发明的各个方面的实施例，其中：

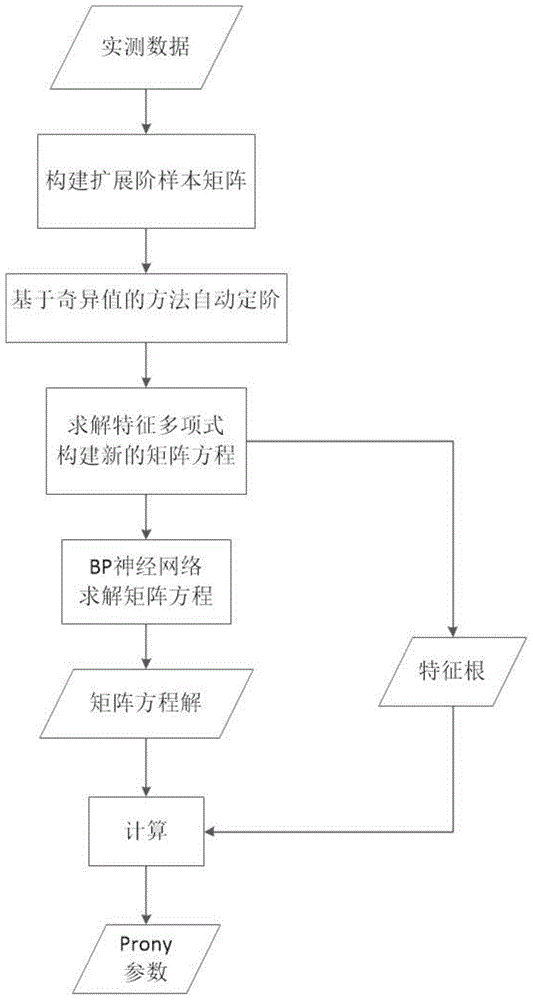
图1是说明根据本发明某些实施方式的适用于低频振荡与次同步振荡辨识的prony分析方法的流程示意图。

图2是说明根据本发明某些实施方式的距离示意图的一个实例图。

图3是说明根据本发明某些实施方式的神经网络结构图。

具体实施方式

为了更了解本发明的技术内容，特举具体实施例并配合所附图式说明如下。

在本公开中参照附图来描述本发明的各方面，附图中示出了许多说明的实施例。本公开的实施例不必定意在包括本发明的所有方面。应当理解，上面介绍的多种构思和实施例，以及下面更加详细地描述的那些构思和实施方式可以以很多方式中任意一种来实施，这是因为本发明所公开的构思和实施例并不限于任何实施方式。另外，本发明公开的一些方面可以单独使用，或者与本发明公开的其他方面的任何适当组合来使用。

根据本发明的实施例，一种适用于低频振荡与次同步振荡辨识的prony分析方法，包括：

步骤1、基于实测数据，构建出扩展阶的样本矩阵；

步骤2、采用基于奇异值分解的方法来确定样本矩阵的有效秩，即prony算法的计算阶数；

步骤3、求解特征多项式，根据求得的特征根构建新的矩阵方程；

步骤4、采用基于bp神经网络的方法进行迭代求解前述构造的矩阵方程；

步骤5、基于前述求解得到的特征根与矩阵方程的解计算prony参数：幅值、衰减因子、频率、初相。

下面结合图1所示的流程图以及本发明的一些优选或者可选的例子，更加具体地描述本发明的某些实例的实施和/或效果。

【数据预处理】

结合附图1，在前述步骤1中，根据样本函数，将实测数据转换为样本矩阵。

样本函数定义如下：

式中，n为采样个数；y(n)为实际采样值。

【算法阶数的选取】

结合附图1，在前述步骤2，基于奇异值分解的方法具体步骤如下：

求得奇异值后，以奇异值的顺序和数值作为横、纵坐标画在坐标系上(如图2)，根据首尾两点(1,σ1)和(pe,σpe)计算直线方程f(x,y)＝0。

根据解析几何的点到直线距离公式，依次计算剩余的点到直线f(x,y)＝0的距离l2、l3、l4、…lpe-1。

选取三个最大距离lk-1、lk、lk+1,可知σk-1、σk、σk+1为拐点区域的奇异值，再求σk-1/σk和σk/σk+1的值，如果σk-1/σk＞＞σk/σk+1，则p＝k-1；如果结果σk-1/σk＜＜σk/σk+1，则p＝k。

实际应用中，为了准确辨识，可选取五个及以内距离最大奇异值相比较。

在确定有效秩p后，即可继续进行prony算法的参数估计。

【新矩阵方程的构造】

结合附图1，当通过特征多项式求得特征根时，在步骤3中将按下述方式构造成新的矩阵方程。

构建的矩阵方程形式如下：

可简化写作：

上式为未知参数bi(i＝1,2,3…p)的矩阵方程，其中，z为特征根构成的vandermonde矩阵，为估计采样值构成的复矩阵，b为未知参数bi构成的实数矩阵。

本步骤中，从特征多项式的求解，可以采用现有技术中公知的技术和手段实现。

【神经网络求解矩阵方程】

结合附图3所示的bp神经网络的示例，在构造好的矩阵方程的基础上，采用bp神经网络对该复矩阵进行求解。

首先，设置复矩阵z的行向量为神经网络的样本，待求复矩阵b设定为权值矩阵，矩阵设定为期望信号；

然后，将该复矩阵方程分解成实部虚部两个方程组来分别进行训练，实数部分进行训练后所比较的期望信号为矩阵，虚数部分进行训练的后所比较的期望信号为0矩阵；

最后，通过误差的反向传播，来调整权值，如此循环直至得到最优结果。

结合附图3所示，下面更加具体地描述求解过程：

附图3中：z′,z″分别为样本矩阵的行向量的实部与虚部；w′,w″为矩阵b的训练结果的实部与虚部；为期望输出的实部与虚部。

将复矩阵z、b分成实部与虚部之和，则得到矩阵方程组：

式中，各变量含义如前所述。

选定权值矩阵的初始值w0，并分解成实部和虚部，在本实施例中直接取零。

按式(2)所示，将在初始权值矩阵的情况下求得输出，与期望输出比较，得到实部与虚部的两组误差列向量。

对误差列向量求平方和，并形成如下的代价函数

其中，

将代价函数对权值矩阵中每个元素求偏导：

权值调整规则：

判断代价函数是否在预设的精度阈值范围之内：若在，此时权值矩阵即为所求的prony参量bi；若不在，则将最新权值矩阵代入式(5)和式(6)中继续计算。

最终求得的参量bi与前述步骤求得的特征根可求得prony参数，即：幅值、衰减因子、频率、初相。

应当理解，前述prony参数的求取，可利用现有技术中方式和手段进行，在本例中不再赘述。

本发明前述一个或多个实施例的实现，是根据基于奇异值绘制的距离示意图中的几何关系来选取奇异值，以此实现样本矩阵有效秩的确定，能够实现自动准确定阶。同时，本发明以bp神经网络求解复矩阵方程，能够避免求解复矩阵广义逆的过程，提升了计算速度。

虽然本发明已以较佳实施例揭露如上，然其并非用以限定本发明。本发明所属技术领域中具有通常知识者，在不脱离本发明的精神和范围内，当可作各种的更动与润饰。因此，本发明的保护范围当视权利要求书所界定者为准。