基于线性分析达到效益最大化的方法与流程

本发明属于企业管理技术领域，特别涉及一种基于线性分析达到效益最大化的方法。

背景技术：

随着信息技术的不断推进，要想快速实现从传统管理到战略成本、效益管理的转型，确保成本、效益管理工作的顺利进行，必须引进先进的管理方法，将成本管理和效益提升的理念、方法融入企业的全价值链业务过程，从而全面提高企业效率、有效节约企业成本。

在市场竞争不断加大、各项成本价格上涨的挑战下，加强内部管理和过程管控，合理调配资源，抓成本提升利润，成为企业生存的重要策略。

降低人、物的消耗，走质量提升的道路，才能保持自己在市场的先进性。怎么在有限的成本管控条件下获得最优的资源配备，达到效益最大化，提升企业市场竞争力同时达到节约成本投入的目的。我们引入了基于线性分析达到效益最大化的方法，从数据上进行呈现和分析，让企业能清晰的识别到资源的投入配比，资源如何最大化利用，从而提升企业整体效益。

技术实现要素：

本发明的目的在于克服现有技术的不足，提供一种采用线性数据分析呈现的方法让企业决策更加符合于实际情况，企业策略人员可以依据此对资源进行针对性调配，从而来获得更大效益，客观地节约了投入成本让企业竞争力加强的基于线性分析达到效益最大化的方法。

本发明的目的是通过以下技术方案来实现的：基于线性分析达到效益最大化的方法，包括以下步骤：

s1、根据业务将问题抽象为数据模型，将最大化效益函数作为目标函数，将业务问题抽象为约束条件数据；

s2、利用线性分析图形化求解最优方案：将人员数量、薪酬金额和社保福利金额作为约束条件，分别进行线性图形化分析，然后获取交点可行区域；转换目标函数，引入效益表达式到目标函数中，然后根据线性图形化呈现得到效益最大的最优数据组合方案。

进一步地，所述步骤s1具体实现方法为：假定需要引进的中级、高级研发人员数量分别为x1和x2，用p代表人员引进后给企业带来的效益量，中、高级技术人员的数量问题以线性规则要素来描述：

目标函数，即为最大化效益：

maxp＝ax1+bx2

其中，a、b分别表示中级技术人员和高级技术人员所带来的效益比；

相应的约束条件如下：

1)招聘引进的总人数限制为x1+x2≤n，x1、x2和n分别表示中级技术人员数量、高级技术人员数量和计划引进总人数；

2)薪酬总投入限制为m1x1+m2x2≤m，m1、m2、m分别表示中级技术人员薪酬、高级技术人员薪酬和计划投入薪酬总额；

3)单月花费的社保福利费用限制p1x1+p2x2≤p，p1、p2和p分别表示中级技术人员社保福利、高级技术人员社保福利和每月计划投入社保总额；

4)人员数量存在非负限制{x1≥0且x2≥0}。

进一步地，所述步骤s2包括以下子步骤：

s1、将约束条件1)引入，进行线性图形化分析：将中级技术人员数量x1作为y轴，高级技术人员数量x2作为x轴，约束条件1)的曲线图；

s22、将约束条件2)引入，进行线性图形化分析：将中级技术人员数量x1作为y轴，高级技术人员数量x2作为x轴，得到约束条件2)的曲线图；

s23、将约束条件3)引入，进行线性图形化分析：将中级技术人员数量x1作为y轴，高级技术人员数量x2作为x轴，得到约束条件3)的曲线图；

s24、取步骤s21～s23三条曲线的与x轴和y轴形成的区域的交集区域，作为交点可行区域；

s25、转换目标函数，引入效益表达式到目标函数中：p＝ax1+bx2，将公示变形为将x1作为y轴，x2作为x轴，则为方程在y轴上的截距；

计划引进总人数为n，产生效益比为a的对象分别按总规划量的为50％、75％、100％来计算，则该对象的数量应为

结合单对象效益比和总效益之间关系获得以下表达式：分别代入方程中，得到三条曲线；

s26、根据线性图形化呈现得到，效益最大的最优数据组合方案：选择三条曲线中与可行区域有交点且在x轴上面的截距最大的曲线，得到该曲线上效益最大的点，将该点的横纵坐标分别作为高级技术人员数量x2和中级技术人员数量x1的值。

本发明的有益效果是：本发明采用线性数据分析呈现的方法让企业决策更加符合于实际情况，企业策略人员可以依据此对资源进行针对性调配，从而来获得更大效益，客观地节约了投入成本让企业竞争力加强。从根本上实现了数字化成本、效益的管理，按此方法进行资源调整配备，提升整体效益的同时让企业竞争力不断加大，在经济效益的整个大环境下生命力才能更强。

附图说明

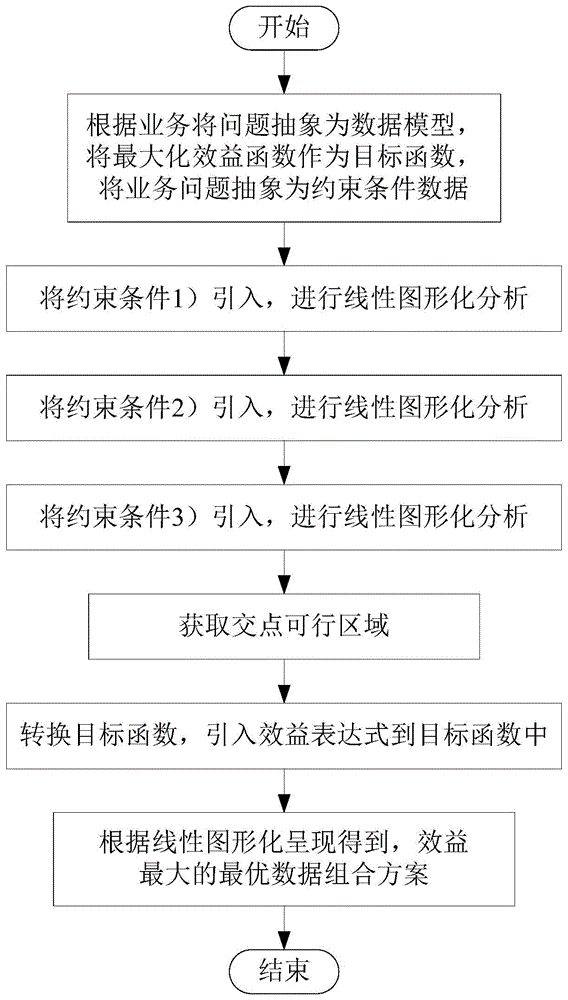
图1为本发明的采用基于线性分析达到效益最大化的方法的流程图；

图2为本发明限制条件一得到的曲线图；

图3为本发明限制条件二得到的曲线图

图4为本发明限制条件三得到的曲线图

图5为本发明得到的可行区域示意图；

图6为本发明目标函数与可行区域相交的曲线图。

具体实施方式

线性图形化求解最优值p：

利用线性分析方法，从约束条件中进行数据图标的分析，找到最优化的图形交点、可行区域，从而获得达到最大效益化的一组对应数据。从而为企业的决策者提供资源调配的依据，间接地进行了成本的控制和效益的增长，让决策更加的科学客观。

约束条件对应松弛：

线性规划的术语中，如a<＝c约束条件的任何未应用的产能都被称为“与对应约束条件对应是松弛的”。

下面结合附图进一步说明本发明的技术方案。

假定软件开发企业预招聘软件开发人员12人，根据实际情况计划招聘中级研发或高级研发或中级、高级按某种比例混合招聘，企业根据实际情况针对新招聘人员最多可以投入的薪酬成本为100000元/月和社保福利费用25000元/月，不同级别的单位人员需要投入的成本不同所需的薪酬和社保福利不同。预计中级研发人员以(m1，p1)(11100,1500)表示单位人员所需要花费的薪酬和社保福利费用，高级研发人员以(m2，p2)(15000，3000)表示单位人员所花费的薪酬和社保福利费用。假设招聘的中级和高级研发人员在入职后所带来的效益比为5和7，如何来决策中级和高级技术人员需求的比例才能使效益达到最大化，我们采用了基于线性分析的方法来实现效益的提升。

本发明采用基于线性分析达到效益最大化的方法来解决上述问题，具体流程如图1所示，包括以下步骤：

s1、根据业务将问题抽象为数据模型，将最大化效益函数作为目标函数，将业务问题抽象为约束条件数据；

假定需要引进的中级、高级研发人员数量分别为x1和x2，用p代表人员引进后给企业带来的效益量，中、高级技术人员的数量问题以线性规则要素来描述：

目标函数，即为最大化效益：

maxp＝5x1+7x2

相应的约束条件如下：

1)招聘引进的总人数限制为x1+x2≤12，即企业引进的技术人员总数不能超过计划引进的总人数；

2)薪酬总投入限制为11100x1+15000x2≤100000，即引进的中级、高级人员每月薪酬合计不能超过计划投入的资金总额；

3)单月花费的社保福利费用限制1500x1+3000x2≤25000，针对引进的技术人员社保福利投入每月不能超过计划投入额；

4)人员数量存在非负限制{x1≥0且x2≥0}。

s2、利用线性分析图形化求解最优方案：将人员数量、薪酬金额和社保福利金额作为约束条件，分别进行线性图形化分析，然后获取交点可行区域；转换目标函数，引入效益表达式到目标函数中，然后根据线性图形化呈现得到效益最大的最优数据组合方案；

限制条件中有{x1≥0且x2≥0}，所以x1和x2都为正值计算，即都在坐标轴的第一象限；具体包括以下子步骤：

s1、将约束条件1)x1+x2≤12引入，进行线性图形化分析：将中级技术人员数量x1作为y轴，高级技术人员数量x2作为x轴，约束条件1)的曲线图，如图2所示；其中直线的斜率为-1，在x轴的截点为(12，0)，在y轴的截点为(0，12)，直线与x轴和y轴中间的任意一点均可以满足约束条件；

s22、将约束条件2)11100x1+15000x2≤100000引入，进行线性图形化分析：将中级技术人员数量x1作为y轴，高级技术人员数量x2作为x轴，得到约束条件2)的曲线图，如图3所示；从图形中可以看出限制条件2教限制条件1更加的严格，xy轴与直线11100x1+15000x2≤100000之间的面积更小；

s23、将约束条件3)1500x1+3000x2≤25000引入，进行线性图形化分析：将中级技术人员数量x1作为y轴，高级技术人员数量x2作为x轴，得到约束条件3)的曲线图，如图4所示；

s24、取步骤s21～s23三条曲线的与x轴和y轴形成的区域的交集区域，作为交点可行区域，如图5所示；

s25、转换目标函数，引入效益表达式到目标函数中：p＝5x1+7x2，将公示变形为将x1作为y轴，x2作为x轴，则为方程轴上的截距；

计划引进总人数为n，产生效益比为5的对象分别按总规划量的为50％、75％、100％来计算，则该对象的数量应为6、9、12；

结合单对象效益比和总效益之间关系获得以下表达式：分别代入方程中，得到三条曲线；如图6所示；

s26、根据线性图形化呈现得到，效益最大的最优数据组合方案：选择三条曲线中与可行区域有交点且在x轴上面的截距最大的曲线，得到该曲线上效益最大的点，将该点的横纵坐标分别作为高级技术人员数量x2和中级技术人员数量x1的值。

当时，三条曲线为三条等效益线，效益p最大时，的值也最大；可以看出，这条线在x轴上面的截距最大，也与可行区域有交点。因此最大效益点为时曲线与y轴的交点，即x2＝0，效益p＝45。

在求解最优解之后将x1＝9，x2＝0带入方程式中进行计算，结果如下：

x1+x2＝9≤12

11100x1+15000x2＝99900≤100000

1500x1+3000x2＝13500≤25000

结果进行汇总如表一所示。

表一

从计算方法可以看出，人员数量上还有3个单位数量，薪酬金额还有100个单位未使用，综上可以看出“社保福利”和“研发人员数量”这两个变量对“薪酬金额”是松弛的，基于线性分析规划中描述为：a<＝c约束条件的任何未使用的产能都称之为“与约束条件对应松弛”，该变量的松弛部分对目标函数没有贡献度，多余出来的社保福利和研发人员数量对效益无贡献，可以针对此两项进行调整。

从数据分析可以得到对应的分析结果，企业策略人员可以依据此对资源进行针对性调配，从而来获得更大效益，客观地节约了投入成本让企业竞争力加强。

针对线性分析达到效益最大化的方法，采用线性数据分析呈现的方法让企业决策更加符合于实际情况，从根本上实现了数字化成本、效益的管理，按此方法进行资源调整配备，提升整体效益的同时让企业生命力更强。

本领域的普通技术人员将会意识到，这里所述的实施例是为了帮助读者理解本发明的原理，应被理解为本发明的保护范围并不局限于这样的特别陈述和实施例。本领域的普通技术人员可以根据本发明公开的这些技术启示做出各种不脱离本发明实质的其它各种具体变形和组合，这些变形和组合仍然在本发明的保护范围内。