一种基于剪枝的卷积神经网络压缩方法、系统及介质与流程

本发明属于卷积神经网络压缩
技术领域：
，具体涉及基于剪枝的卷积神经网络压缩方法。
背景技术：
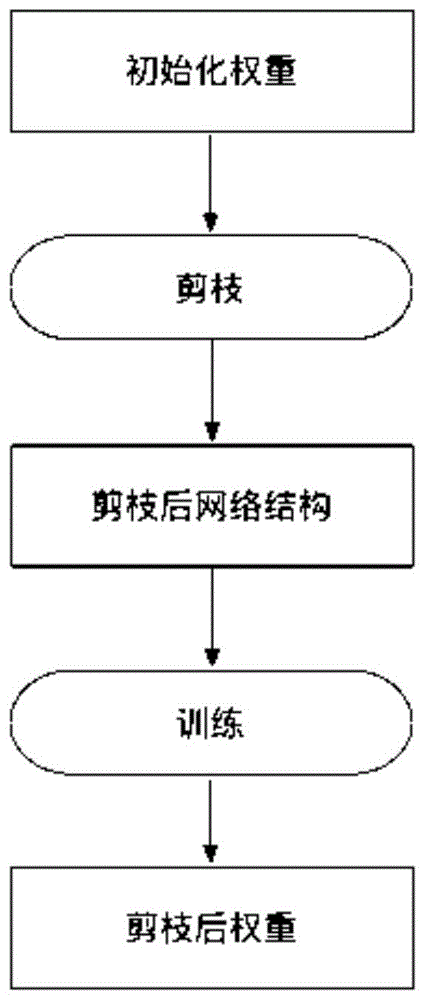
：近年来，深度神经网络在解决诸如图像分类，人脸识别等计算机视觉任务上表现极为出色，而在不同类型的的神经网络当中，卷积神经网络是表现极为出色的一种。随着卷积神经网络的发展，网络层次逐渐加深，参数规模变大，这使得卷积神经网络在实际部署上受到了极大的限制。一方面是模型尺寸，卷积神经网络的强大能力来自数以百万计的可训练参数。这些参数以及网络结构信息需要存储在磁盘上，并在推理期间加载到存储器中。例如，存储在imagenet上训练的典型网络模型会占用超过300mb的空间，这对嵌入式设备来说是一个很大的资源负担；另一方面是运行时内存，在推理期间，即使批量大小为1，卷积神经网络的中间激活/响应甚至可能比存储模型参数占用更多的内存空间。这对于高端gpu来说不是问题，但是对于计算能力低的移动设备和嵌入式设备来说，这是不可承受的。因此，对模型进行剪枝以减少模型的大小很有必要。深度卷积神经网络的模型参数重有很多冗余，可以寻找一种有效的评判手段来判断参数重要性，将不重要的连接或者滤波器进行裁剪来减少模型的冗余，使模型变得更加稀疏，减少计算量。典型的模型剪枝方法包含三步：训练，剪枝和微调，iccv2017的论文networkslimming详细的介绍了这种方法，但是此种方法为了达到较好的准确率，通过需要耗费较长的微调时间。目前最新的剪枝方法rethinkingthevalueofnetworkpruning发现通过剪枝得到的模型结构从头开始训练可以得到和微调相当甚至更好的结果。技术实现要素：本发明旨在解决以上现有技术的问题。提出了一种基于剪枝的卷积神经网络压缩方法、系统及介质。本发明的技术方案如下：一种基于剪枝的卷积神经网络压缩方法，其包括以下步骤：(1)获取训练数据并对训练数据进行预处理，包括随机裁剪、随机垂直翻转以及正则化；(2)初始化卷积神经网络模型的权重；(3)计算网络连接的显著度，以显著度的分数作为评估连接重要性的标准，并对显著度进行排序，其中为了减少计算量以加快剪枝过程，采用了泰勒展开式近似分析剪枝对于损失函数带来的影响；(4)对卷积神经网络进行剪枝，将剪枝定义为优化问题如式(1)所示,式(1)中l(x,y；θ)代表训练模型的损失函数，x代表输入数据，y是对应的标签，θ∈rm代表模型的参数；剪枝即选择所有连接的子集并从网络中移除参数那么余下的参数记作因此，为了最小化损失函数的增长需要选择合适的c*；保留top-k的连接，使得网络稀疏化；(5)训练稀疏化后的卷积神经网络模型，直到模型收敛。进一步的，所述步骤(1)对训练数据进行预处理，具体步骤为：步骤2.1:对于要使用的数据集划分为训练集和测试集，二者的比例为9:1，同时以数据集的一个批次作为训练样本，使用的批次大小为128，所选取的批次公式如式(2)所示，式(2)中d代表数据集，x代表输入数据，y是对应的标签，i代表当前批次。进一步的，所述步骤(2)初始化卷积神经网络模型的权重，具体步骤为：步骤3.1:采用方差初始化方法初始化卷积神经网络模型的权重。进一步的，所述步骤(3)计算网络连接的显著度，以显著度的分数作为评估连接重要性的标准，并对显著度进行排序，具体步骤为：步骤4.1:用特征图z表示连接k的输出，用可训练的缩放因子g∈{0,1}m乘以z并用进行后面的计算，当gi是0的时候，相当于连接k被剪掉，因此可将式(1)改写成优化方程如式(3)所示，△l(x,y)(g)＝|l(x,y)(g)-l(x,y)(0)|式(3)步骤4.2:采用taylor级数展开式扩展(3)中的l(x,y)(0)为方程如式(4)(5)所示，式(4)中的ri(g)表示拉格朗日余项，式(5)中的r1(g)表示一阶展开后的拉格朗日余项。步骤4.3:结合式(3)和式(5)，可得到优化方程如式(6)所示，步骤4.4：拉格朗日余项r1会带来大量的计算，为了节省计算量将其省略，因此显着度分数可以通过反向传播计算得到，对于每个连接ci∈c，采用s(gi)作为显著度分数，s(gi)由式(7)计算得到，步骤4.5:将显著度分数按从大到小排序。进一步的，所述步骤(4)对卷积神经网络进行剪枝，保留top-k的连接，使得网络稀疏化，具体步骤为：步骤5.1:预先设定剪枝模型的稀疏级别，其中稀疏级别如式(8)所示，式(8)中，m代表所有的参数数目，κ代表期望非零的参数数目；步骤5.2:在给定稀疏度之后，可以任意断开网络模型中的连接并保留绝对值最大的κ％连接。一种基于剪枝的卷积神经网络压缩系统，其包括：预处理模块：用于获取训练数据并对训练数据进行预处理，包括随机裁剪、随机垂直翻转以及正则化；初始化模块：用于初始化卷积神经网络模型的权重；显著度计算排序模块：用于计算网络连接的显著度，以显著度的分数作为评估连接重要性的标准，并对显著度进行排序；剪枝模块：用于对卷积神经网络进行剪枝，将剪枝定义为优化问题如式(1)所示,式(1)中l(x,y；θ)代表训练模型的损失函数，x代表输入数据，y是对应的标签，θ∈rm代表模型的参数；剪枝即选择所有连接的子集并从网络中移除参数那么余下的参数记作因此，为了最小化损失函数的增长需要选择合适的c*；保留top-k的连接，使得网络稀疏化；训练模块：用于训练稀疏化后的卷积神经网络模型，直到模型收敛。一种介质，该介质内部存储计算机程序，其所述计算机程序被处理器读取时，执行上述权任一项的方法。本发明的优点及有益效果如下：本发明针对卷积神经网络参数冗余，浮点运算数过多的问题，本发明提供了一种基于剪枝的卷积神经网络压缩方法，可以在简化剪枝流程的同时训练出更加稀疏的网络。本发明的优点是在初始化权重之后通过连接敏感度分数结构化地选择重要的连接并对网络进行裁剪，省去了耗时的预训练和微调流程，随后通过正常的训练可以得到更加稀疏化的网络结构并保持了原网络模型的准确率。附图说明图1是本发明提供优选实施例基于剪枝的卷积神经网络压缩整体流程图；图2是本发明方法将vgg-d模型在cifar-10数据集上的测试准确率变化图；图3是本发明方法将vgg-d模型在cifar-10数据集上的loss变化图。具体实施方式下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、详细地描述。所描述的实施例仅仅是本发明的一部分实施例。本发明解决上述技术问题的技术方案是：本发明所建立模型的实验平台如下：ubuntu16.04系统，采用geforcegtx1070显卡，采用tensorflow框架来进行网络的训练与测试。下面以公开数据集cifar-10为例，结合附图1与具体实施方式对本发明作进一步详细描述，其中cifar-10是一个彩色图像数据集，共有10个类别，分别为飞机、汽车、鸟类、猫、鹿、狗、蛙类、马、船、和卡车，每张图片的尺寸为32×3，整个数据集有50000个训练图像和10000个测试图像，每个类别占十分之一，图1为卷积神经网络压缩整体结构流程图：步骤1:对训练数据进行预处理；步骤2:初始化卷积神经网络模型的权重；步骤3:计算网络连接的显著度，以显著度的分数作为评估连接重要性的标准，并对显著度进行排序；步骤4:对卷积神经网络进行剪枝，保留top-k的连接，使得网络稀疏化；步骤5:训练稀疏化后的卷积神经网络模型，直到模型收敛；以下详细说明本发明中各个步骤实施的细节问题：步骤1:对训练数据进行预处理。具体的，对于要使用的数据集划分为训练集和测试集，二者的比例为9:1，同时以数据集的一个批次作为训练样本，使用的批次大小为128，所选取的批次公式如式(2)所示，式(2)中d代表数据集，i代表当前批次。步骤2:所述卷积神经网络压缩方法采用方差初始化方法初始化卷积神经网络模型的权重。步骤3:计算网络连接的显著度，以显著度的分数作为评估连接重要性的标准，并对显著度进行排序。卷积神经网络模型中具有k个连接，本发明所述方法为了避免在一次剪枝过程中对连接计算k次，使用taylor展开式来近似分析剪枝对于损失函数带来的影响，以下步骤为近似计算的具体步骤：步骤3-1:用特征图z表示连接k的输出，用可训练的缩放因子g∈{0,1}m乘以z并用进行后面的计算，当gi是0的时候，相当于连接k被剪掉，因此可将式(1)改写成优化方程如式(3)所示，△l(x,y)(g)＝|l(x,y)(g)-l(x,y)(0)|式(3)步骤3-2:采用taylor级数展开式扩展(3)中的l(x,y)(0)为方程如式(4)(5)所示，式(4)中的ri(g)表示拉格朗日余项，式(5)中的r1(g)表示一阶展开后的拉格朗日余项。步骤3-3:结合式(3)和式(5)，可得到优化方程如式(6)所示，步骤3-4：拉格朗日余项r1会带来大量的计算，为了节省计算量本发明将其省略。因此显着度分数可以轻易地通过反向传播计算得到，对于每个连接ci∈c，采用s(gi)作为显著度分数，s(gi)由式(7)计算得到，步骤3-5:将显著度分数按从大到小排序。步骤4:对卷积神经网络进行剪枝，保留top-k的连接，使得网络稀疏化。步骤4-1:预先设定剪枝模型的稀疏级别，其中稀疏级别如式(8)所示，式(8)中，m代表所有的参数数目，κ代表期望非零的参数数目。步骤4-2:在给定稀疏度之后，可以任意断开网络模型中的连接并保留绝对值最大的κ％连接。步骤5:训练稀疏化后的卷积神经网络模型，直到模型收敛。预训练参数如下：参数项参数值learningrate0.1weightdecay0.0005trainbatch128maxiterations150000optimizermomentum在训练过程中，学习率衰减如下：迭代次数学习率300000.02600000.004900000.00081200000.00016图2是vgg-d模型在稀疏级别为95％时的准确率变化图，可以看到本发明所述方法可以在减少参数量的同时保持原模型的准确率，图3是vgg-d模型在稀疏级别为95％时的loss变化图，可以看到本发明所述方法可以有效地降低损失函数值，使模型更快达到收敛。本发明在训练之前对网络进行裁剪，省去了预训练和微调流程，极大地简化了剪枝过程的同时保持了网络的准确率，同时通过显著度分数结构化地选择重要的连接，对于不同的网络结构具有鲁棒性，因此可以应用到多种网络结构中而不需要进行过多的调整。除此之外，本方法选用数据集中的一个批次来决定重要的连接，可以通过不同的批次来验证留下的连接是否对于指定的任务是有效的。以上这些实施例应理解为仅用于说明本发明而不用于限制本发明的保护范围。在阅读了本发明的记载的内容之后，技术人员可以对本发明作各种改动或修改，这些等效变化和修饰同样落入本发明权利要求所限定的范围。当前第1页12