一种基于Lévy飞行的粒子群算法的生产计划优化方法与流程

本发明属于生产计划优化领域，尤其涉及一种基于lévy飞行的粒子群算法的生产计划优化方法。

背景技术：

随着近些年来流程工业的整体市场情况的波动，间歇式生产模式逐渐兴起，其能够带给流程工业的优势也愈发明显。流程工业的企业面对复杂多变的市场环境，想要提高自身的竞争力，就必须根据市场需求制定合理的生产计划，生产计划的目的是要在充分考虑市场需求与企业生产能力的情况下，调整企业各部门间的协作关系来提高效益。生产计划的模型应由不同部门间的费用模型组建，包括生产费用、运输费用、短缺费用和仓储费用，并进行统筹规划，使得这些费用的总和最小。随着生产计划规模的扩大，生产计划求解的难度急剧加大，传统粒子群算法难以求得高质量的解，对于一些非线性问题传统解法也无能为力。

技术实现要素：

本发明主要解决了基本粒子群算法优化生产计划易陷入局部最优、收敛速度慢、精度低的缺点，提供了一种能够提高生产计划求解的速度和精度，对于非线性问题亦有一定优势的基于lévy飞行的粒子群算法的生产计划优化方法。

本发明解决其技术问题所采用的技术方案是，一种基于lévy飞行的粒子群算法的生产计划优化方法，包括以下步骤：

步骤1：建立生产计划模型；

步骤2：初始化参数，该参数包括种群的粒子数n、维度d、学习因子c1和c2、迭代次数ger、初始概率p0、结束概率p1、初始惯性权重ω0和结束惯性权重ω1；

步骤3：初始化粒子的位置，并将粒子的个体最优位置pid设置为当前位置；

步骤4：计算各个粒子的目标函数值，如果fit(xid)优于fit(pid)，则更新pid为xid的当前值，否则pid不变；

其中，fit(xid)和fit(pid)分别为目标函数在xid和pid的适应度值，xid为粒子在当前迭代中第d维的值，pid为粒子在当前迭代过程中第d维的个体最优值；

步骤5：如果fit(xid)优于fit(pgd)，则更新pgd为xid的当前值，否则pgd不变；

其中，fit(pgd)为目标函数在当前全局最优点的适应度值；

步骤6：进行粒子位置更新；

步骤7：判断是否达到最大迭代次数/达到目标函数的收敛精度，若是，则结束，输出结果；若否，返回步骤4。

以生产计划模型中各个影响生产成本的因素集合为粒子群，通过粒子群算法求解各个因素最优值，以实现生产成本最优。

作为上述方案的一种优选方案，所述的目标函数如下：

式中，n表示生产调度周期，n表示周期集合，s表示产品，s表示产品集合，α,β,γ,δ分别表示所对应种类产品生产费用单价、运输费用单价、短缺费用单价及贮存费用单价，分别表示在调度周期n内产品s的生产量、运输量、短缺量和贮存量。

作为上述方案的一种优选方案，所述生产计划模型如下：

式中，表示生产调度周期n-1内，产品s的贮存量，表示调度周期n内产品s的客户订单量，为产品s的最大生产量。

作为上述方案的一种优选方案，所述步骤6中采用加入lévy飞行的位置更新公式和基本粒子群位置更新公式中的一种位置更新公式对粒子位置进行更新。采用两种位置更新公式更新粒子位置，解决了传统粒子群算法易陷入局部最优的问题。

作为上述方案的一种优选方案，所述采用加入lévy飞行的位置更新公式进行粒子位置更新的概率为p，采用基本粒子群位置更新公式进行粒子位置更新的概率为1-p。概率p的公式如下：

式中，p0和p1分别为开始和结束时的概率值，i为当前的迭代次数，ger为总迭代次数。根据概率来决定采用何种位置更新公式，且这个概率随着迭代次数的改变而改变，加快了收敛速度，提高了收敛精度。

作为上述方案的一种优选方案，所述加入lévy飞行的位置更新公式如下：

式中，c1和c2是学习因子，为常数；r1和r2为[0,1]内均匀分布的随机数；和分别是粒子在第k+1次和第k迭代中第d维的位置，两者均有上下限，是粒子pi在第k次迭代中第d维的个体最优位置，pgd是种群的第d维的全局最优位置，ω为惯性权重，α0为系数，常取α0＝0.01，为点乘积，levy(β)为随机搜索路径，表示服从参数为β的莱维分布，levy(β)～|t|^-β,0＜β≤3。

作为上述方案的一种优选方案，采用mantegna对莱维分布进行模拟，表达式如下：

式中，μ,v为正态分布，定义μ～n(0,σ²)，v～n(0,1)；

式中，

式中，γ(·)为gamma函数，常取β＝1.5。

作为上述方案的一种优选方案，所述惯性权重ω随着迭代次数增加逐渐减小，其公式如下：

式中，ω0和ω1分别为初始和最终的惯性权重值，i为当前的迭代次数，ger为总迭代次数。

本发明的有益效果是：采用两种粒子群位置更新方式，根据概率来决定采用何种更新方式，能够更好的跳出局部最优，收敛到全局最优，在加快了收敛速度的同时提高了收敛精度，能够更快的获得最优生产计划。

附图说明

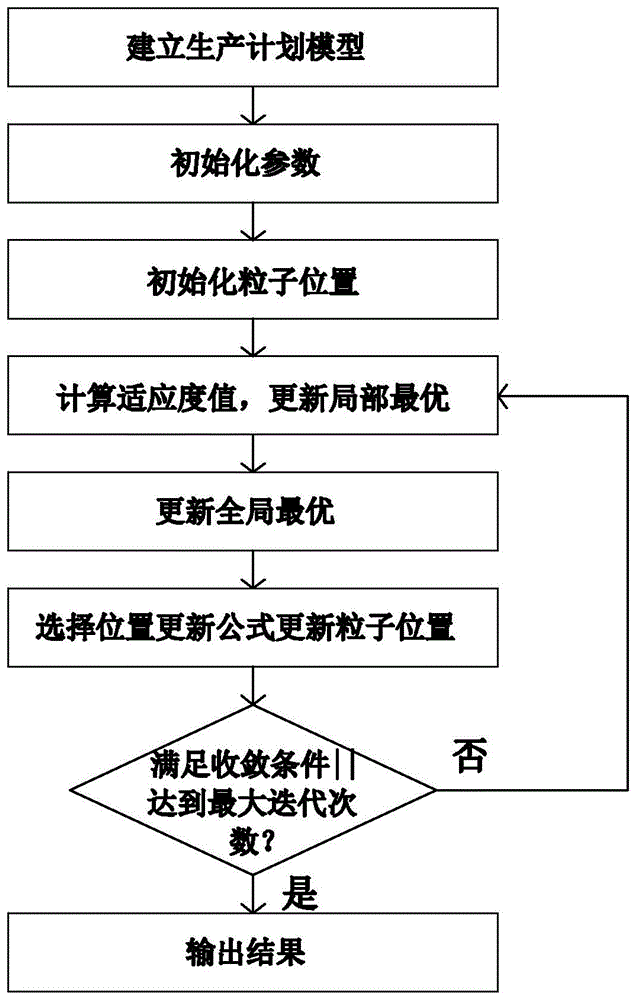
图1为实施例中基于lévy飞行的粒子群算法的生产计划优化方法的一种流程示意图。

具体实施方式

下面通过实施例，并结合附图，对本发明的技术方案作进一步的说明。

实施例：

本实施例一种基于lévy飞行的粒子群算法的生产计划优化方法，如图1所示，包括以下步骤：

步骤1：建立生产计划模型，本实施例中考虑的因素包括生产量、运输量、短缺量和贮存量，最终建立的生产计划模型如下：

式中，表示生产调度周期n-1内，产品s的贮存量，表示调度周期n内产品s的客户订单量，为产品s的最大生产量；

步骤2：初始化参数，该参数包括种群的粒子数n、维度d、学习因子c1和c2、迭代次数ger、初始概率p0、结束概率p1、初始惯性权重ω0和结束惯性权重ω1；

步骤3：初始化粒子的位置，并将粒子的个体最优位置pid设置为当前位置；

步骤4：计算各个粒子的目标函数值，目标函数如下：

式中，n表示生产调度周期，n表示周期集合，s表示产品，s表示产品集合，α,β,γ,δ分别表示所对应种类产品生产费用单价、运输费用单价、短缺费用单价及贮存费用单价，分别表示在调度周期n内产品s的生产量、运输量、短缺量和贮存量；如果fit(xid)优于fit(pid)，则更新pid为xid的当前值，否则pid不变；其中，fit(xid)和fit(pid)分别为目标函数在xid和pid的适应度值，xid为粒子在当前迭代中第d维的值，pid为粒子在当前迭代过程中第d维的个体最优值，本实施例中fit(xid)小于fit(pid)即为fit(xid)优于fit(pid)；

步骤5：如果fit(xid)优于fit(pgd)，则更新pgd为xid的当前值，否则pgd不变；fit(pgd)为目标函数在当前全局最优点的适应度值；

步骤6：进行粒子位置更新；粒子位置更新采用采用加入lévy飞行的位置更新公式和基本粒子群位置更新公式中的一种，采用加入lévy飞行的位置更新公式进行粒子位置更新的概率为p，采用基本粒子群位置更新公式进行粒子位置更新的概率为1-p。概率p的公式如下：

式中，p0和p1分别为开始和结束时的概率值，i为当前的迭代次数，ger为总迭代次数；本实施例中采用生成随机数r的形式实现位置更新公式的选择，当随机数r＞p时采用原基本粒子群位置更新公式，当r≤p时采用加入lévy飞行的位置更新公式，r为[0,1]内的均匀随机数，本实施例中，p0＝0.8，p1＝0。

其中，加入lévy飞行的位置更新公式如下：

式中，c1和c2是学习因子，为常数；r1和r2为[0,1]内均匀分布的随机数；和分别是粒子在第k+1次和第k迭代中第d维的位置，两者均有上下限，是粒子pi在第k次迭代中第d维的个体最优位置，pgd是种群的第d维的全局最优位置，ω为惯性权重，α0为系数，常取α0＝0.01，为点乘积，levy(β)为随机搜索路径，表示服从参数为β的莱维分布，levy(β)～|t|^-β,0＜β≤3，莱维分布十分复杂，实现难度高，因此本实施例中采用mantegna方法模拟进行模拟，mantegna方法表达式如下：

式中，μ,v为正态分布，定义μ～n(0,σ²)，v～n(0,1)。

式中，

式中，γ(·)为gamma函数，常取β＝1.5。

惯性权重ω随着迭代次数增加逐渐减小，其公式如下：

式中，ω0和ω1分别为初始和最终的惯性权重值，i为当前的迭代次数，ger为总迭代次数。

步骤7：判断是否达到最大迭代次数或达到目标函数的收敛精度，若是，则结束，输出结果，输出的结果pgd包括当前调度周期内产品的生产量、运输量、短缺量和贮存量；若否，返回步骤4。

本文中所描述的具体实施例仅仅是对本发明精神作举例说明。本发明所属技术领域的技术人员可以对所描述的具体实施例做各种各样的修改或补充或采用类似的方式替代，但并不会偏离本发明的精神或者超越所附权利要求书所定义的范围。