一种基于矩阵指数的弹性保持投影方法及其应用与流程

本发明公开了一种维数约简方法-指数弹性保持投影，其属于生物特征提取和模式识别技术领域，涉及数据局部和全局邻域结构的构建、矩阵指数计算、目标函数的优化，可用于图像识别、数据挖掘、数据聚类。

背景技术：

主成分分析(principalcomponentanalysis，pca)和线性判别分析(lineardiscriminationanalysis，lda)作为比较典型的维数约简方法，已经广泛地应用在多个领域。pca的主要目标是寻找使得数据协方差最大的投影方向，该投影方向是通过线性变换得到的一组最优的单位正交向量基，这些向量的线性组合可以重构原始样本，并且重构后的样本和原始样本之间的误差最小。相对于pca方法，lda是一种有监督的维数约简方法，主要目标就是寻找一组线性变换使得样本类内散度最小化的同时，也要使得样本类间散度最大化。但是受到方法本身的限制，lda至多只能提取c-1个特征(c表示样本类别数)，这在很多情况下是不能满足需求的。此外，lda在处理高维图像数据时常常遇到“奇异值”问题：由于原始高维空间中的样本维数远大于样本数，lda中散度矩阵会出现奇异性。随后，为了解决lda的奇异值问题，涌现了许多lda的变体，包括二维线性判别分析(two-dimensionallineardiscriminantanalysis，2dlda)，最大边缘准则(maximummargincriterion，mmc)，基于广义奇异值分解的线性判别分析(ldabasedonthegeneralizedsingularvaluedecomposition，lda/gsvd)，qr分解线性判别分析(ldaviaqrdecomposition，lda/qr)等。通过观察这些算法发现，其基本思想都是通过寻找最优投影向量来捕获数据的全局euclidean几何结构，因此都属于基于全局的算法。虽然这些方法在图像识别领域获得了令人鼓舞的结果，但是它们并没有明确地考虑数据的局部信息。对于分类问题，局部信息也是非常重要的。

相比之下，流形学习利用了数据的局部信息，旨在通过局部信息进而发掘数据的整体非线性结构。局部线性嵌入(locallinearembedded，lle)，拉普拉斯特征映射(laplacianeigenmaps，le)，局部保持投影算法(localitypreservingprojections，lpp)，近邻保持投影(neighborhoodpreservingprojection，npp)等都是代表性的流形学习方法。可是后来研究者发现，在模拟多重流形的时候，仅仅考虑局部信息是远远不够的。继而促进了非监督辨别投影(unsuperviseddiscriminantprojection，udp)，弹性保持投影(elasticpreservingprojection，epp)，辨别正交弹性保持投影(orthogonaldiscriminantelasticpreservingprojection，doepp)等方法的出现。这些方法存在一个共性：通过将全局(或者非局部)和局部结构信息引入目标函数，从而来发掘数据最重要的辨别流形结构。但是，这些方法仍然存在两个问题：(1)当样本数远小于数据维数时，导致所谓的小样本问题；(2)通常是利用k最近邻准构建局部图模型，从而导致模型不一定符合数据真实的内在局部结构，使算法容易受到邻域参数k的影响。

技术实现要素：

本发明针对目前维数约简算法中存在的小样本问题(奇异值问题)、对邻域参数敏感、未考虑数据本身的结构信息等问题，提出了一种基于矩阵指数的弹性保持投影方法。

具体的技术方案如下：

基于矩阵指数的弹性保持投影方法，其特征为：包括如下步骤：

步骤1.为了捕获图像数据的局部和全局结构特性，分别构建局部和全局邻域图，并计算权重获得对应相似矩阵slocal和sglobal；

步骤2.根据相似矩阵计算拉普拉斯矩阵；

步骤3：进行矩阵指数运算并定义目标函数；

步骤4：目标函数优化求解。

本发明还公开一种应用于特征提取(维数约简)和模式识别的产品，其特征为：该产品包括上述基于矩阵指数的弹性保持投影方法。

与现有的研究相比较，本发明具有如下的优点：

(1)本发明通过引入矩阵指数运算，一方面避免了小样本问题(奇异值问题)，另一方面减少了算法对邻域参数的敏感性。

(2)本发明相对于弹性保持投影算法，不仅考虑了数据的本质几何结构，还提升了算法的鲁棒性。

(3)本发明通过最大化全局结构和最小化局部结构，实现了对原始数据几何结构的考虑。

附图说明

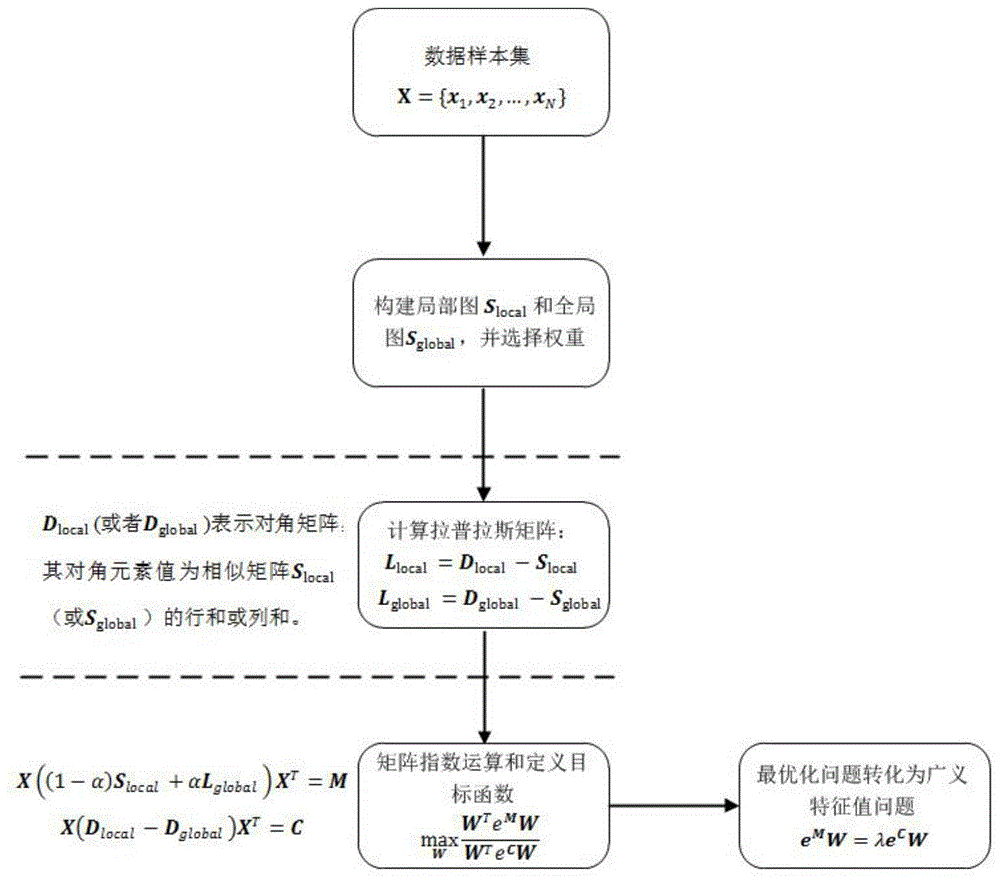
图1为本发明基于矩阵指数的弹性保持投影方法及其应用流程示意图。

具体实施方式

以下描述用于揭露本发明以使本领域技术人员能够实现本发明。以下描述中的优选实施例只作为举例，本领域技术人员可以想到其他显而易见的变型。

对于人脸识别问题，给定一个人脸图像训练样本集x＝{x1，x2，...，xn}∈r^d×n，xi表示由人脸图像拉成的d维特征向量，例如对于一个100向100像素的人脸图像，展开后就是d＝10000维的特征向量。n表示训练样本数。本发明目的就是找到一个转换矩阵w∈r^d×d，并利用此转换矩阵得到人脸数据的低维嵌入：yi＝w^txi，yi∈r^d×n，其中d＜d，从而降低数据维数。最终，可在低维空间实现对人脸图像的分类识别。

基于矩阵指数的弹性保持投影方法，其特征为：包括如下步骤：

步骤1.为了捕获人脸图像数据的局部和全局结构特性，分别构建其局部和全局邻域图，并计算权重获得对应相似矩阵。

所述步骤1进一步包括如下内容：

(1)构建局部邻域图和计算相似矩阵：采用k近邻准则构造数据局部邻域图，即，如果人脸图像样本xj包含在距离图像样本xi最近的k个样本之内，就认为点i和j有边相连；否则，认为无边相连。然后，根据构建的局部领域图，定义数据的局部相似矩阵slocal：

其中参数t≥0。

(2)构建全局图和计算相似矩阵：为了挖掘数据的全局几何结构，反映任意两个人脸图像样本之间的关系，全局相似矩阵sglobal可以定义为：

其中σ≥0。

所述步骤2进一步包括如下内容：

根据步骤1)中获得的相似矩阵slocal和sglobal计算相应拉普拉斯矩阵有：

llocal＝dlocal-slocal(1.3)

lglobal＝dglobal-sglobal(1.4)

其中，dlocal(或dglobal)表示对角矩阵，其对角元素值为相似矩阵slocal(或sglobal)的行和或列和。

步骤3：对所述矩阵运算和目标函数定义，进一步包括如下内容：

令

x((1-α)slocal+αlglobal)x^t＝m(1.5)

x(dlocal-dglobal)x^t＝c(1.6)

其中α表示平衡参数且0＜a＜1。

对于任意一个方阵a∈r^n×n，其指数形式可以写作：

其中，i表示n×n的单位矩阵。

矩阵指数的性质有：e⁰＝i；e^ae^-a＝i；e^a是一个满秩矩阵。

因此，为了利用局部结构寻求嵌入在高维空间中非线性流形，同时利用全局信息发现高维空间的欧氏结构，基于矩阵指数的弹性保持投影的目标函数可以定义为：

其中φm＝[φm1，φm2，…，φmn]表示由m的特征向量所构成的矩阵，且对应的特征值为am＝[λm1，λm2，...，λmn]。同样，φc＝[φc1，φc2，...，φcn]表示c的特征向量所形成的矩阵，对应的特征值为λc＝[λc1，λc2，...，λcn]。

步骤4：目标函数优化求解，进一步包括如下内容：

引进矩阵指数后，e^c是满秩的，以至于能够提取隐含在矩阵c零空间和非零空间的辨别信息。同时，通过矩阵指数运算以后，特征值会由λ1，λ2，...，λn变为由于指数的性质可得，特征值越小，其所占比例将越小；特征值越大，其所占比例将更大。最终。由邻域参数k变化所引起的小的特征值被削弱，较大特征值也会被放的更大，进而使得算法对于邻域k具有很强的鲁棒性。

最后，式(1.8)最优化问题可以转化为以下广义特征值问题：

e^mw＝λe^cw(1.9)

最优投影矩阵w＝[w1，w2，...，wd]由求解上式广义特征值问题得到的d个最大特征值对应的特征向量组成。利用最优投影矩阵可求得每一张人脸图像的低维嵌入：yi＝w^txi，yir^d×n，其中d＜d。整个优化求解过程不仅可以保留人脸图像的重要特征，消除冗余特征，且原始人脸图像的特征维数由d减小到d，大大较少了计算复杂度，进而可利用分类器在低维空间进行人脸识别。

本发明采用基于矩阵指数的弹性保持投影方法一方面，通过构建局部和全局图来挖掘数据的本质结构信息；另一方面，通过引入矩阵指数计算，使矩阵满秩，从而解决小样本问题，同时，引入矩阵指数后，由邻域参数变化所引起的小的特征值被削弱，较大特征值会被放的更大，以至于可增强算法对领域参数的鲁棒性。

以上显示和描述了本发明的基本原理、主要特征和本发明的优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是本发明的原理，在不脱离本发明精神和范围的前提下本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明的范围内。本发明要求的保护范围由所附的权利要求书及其等同物界定。