一种基于剪切波的双重图像去噪方法与流程

本发明属于图像处理方法技术领域，涉及一种基于剪切波的双重图像去噪方法。

背景技术：

随着科技的不断进步，图像中包含的信息也越来越被人重视。图像处理是实现图像信息提取的重要前提，而在图像信息被提取或传输时容易受到不同类型噪声干扰，图像中的噪声会使图像质量大大降低，甚至模糊了图像的特征，掩盖了重要信息，造成图像的失真，因此对图像进行高效的去噪预处理异常重要。在众多学者的研究下，为了能够更好的减少或消除图像中的噪声，产生了许多的图像去噪方法，如小波阈值法、维纳滤波方法、中值滤波方法、高斯滤波方法等。这些方法各自去噪效果却各不相同。

小波阈值法因操作简单，受到了大家的青睐，此方法首先是把图像分为低频序列和高频序列，利用阈值化对高频序列的噪声进行处理，再对修正后的小波系数进行拼接，得到去噪后的图像。小波阈值法去噪效果的关键环节就是阈值的估量和阈值函数的选择，阈值选择过小，图像中的噪声会存有残留；选择太大则会覆盖掉图像中的细节特征，导致图像模糊。所以小波阈值函数去噪声的局限性在于阈值判定准则的选取。其他的一些方法如中值滤波对椒盐噪声去噪效果较好，空域低通滤波对高斯噪声去噪效果较好，但是这几种方法在去噪的同时模糊甚至是破坏了图像的边缘细节，影响了图像整体的去噪效果。

技术实现要素：

本发明的目的是提供一种基于剪切波的双重图像去噪方法，解决了现有技术中存在的去噪时模糊甚至破坏图像边缘细节的问题。

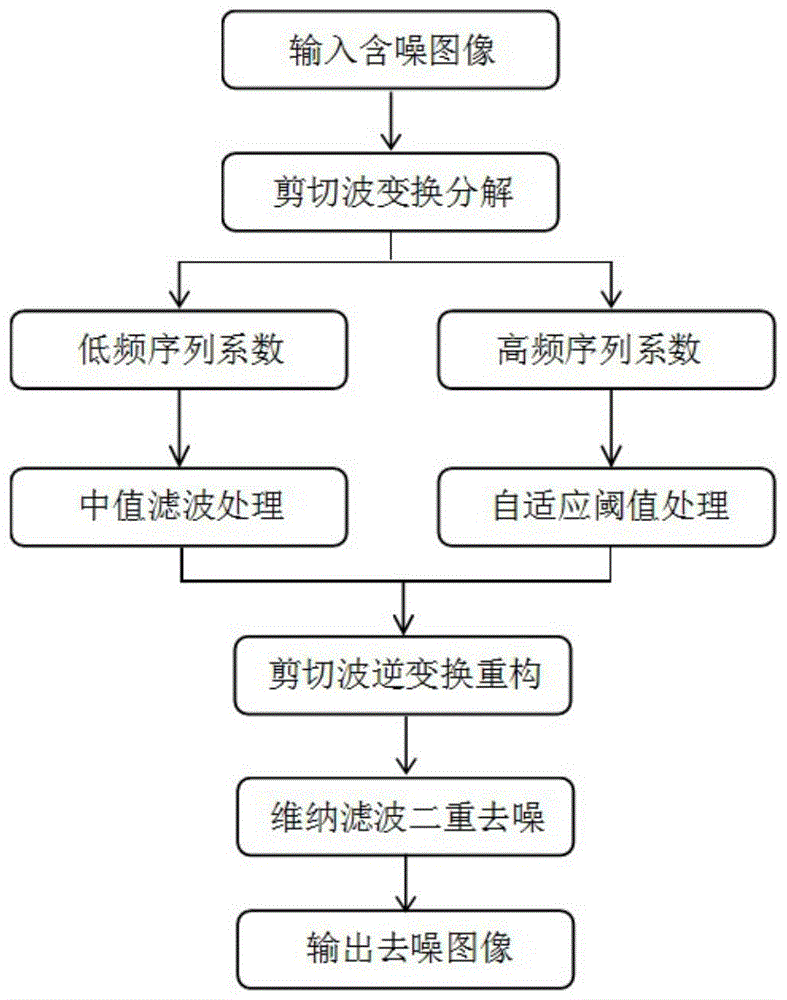
本发明所采用的技术方案是，一种基于剪切波的双重图像去噪方法，包括：

步骤1、对噪声图像f(x,y)进行分解，得到不同尺度的低频序列和高频序列；

步骤2、分别对低频序列、高频序列进行去燥处理；

步骤3、将经步骤2处理后的低频序列、高频序列进行逆变换，得到一重去噪后的图像f1；

步骤4、对图像f1进行二重去噪，得到图像f2。

本发明的特点还在于，

步骤1具体过程为：采用剪切波变换对噪声图像f(x,y)进行分解，得到水平和竖直方向低频序列ll、水平低频和竖直高频序列lh、水平高频和竖直高频序列hl、水平高频和竖直高频序列hh。

步骤2中：

采用中值滤波对低频序列ll进行去噪处理，得到低频序列采用自适应阈值t分别对高频序列lh、hl、hh进行去噪处理：

得到高频序列

步骤4中采用维纳滤波对图像f1进行二重去噪处理。

本发明的有益效果是：

本发明的基于剪切波的双重图像去噪方法，采用剪切波多尺度变换分解，克服小波分解不够精细的缺点，能够更好的对弱小信号进行区分，使该变换具有平移不变性和稳定性等优点；特别是对于弱小目标检测，不会因为下采样操作而导致目标信息丢失；对三个高频序列采用自适应阈值法进行去噪处理，能够更好的消除图像中大部分的噪声，保持图像的边缘；对低频序列系数采用中值滤波去噪，能够消除图像中的孤立噪声，更好的维持图像的清晰度；对重构图像f1采用维纳滤波进行二重去噪处理，能更好的处理图像中的高斯噪声和乘性噪声,清除图像中的残留噪声，使图像变得更平滑，能保持图像的纹理结构等信息。

附图说明

图1是本发明一种基于剪切波的双重图像去噪方法的流程图；

图2是本发明一种基于剪切波的双重图像去噪方法的剪切波变换分解示意图；

图3是本发明一种基于剪切波的双重图像去噪方法的维纳滤波原理图；

图4是小波阈值去噪方法去除图像噪声的效果图；

图5是维纳滤波去噪方法去除图像噪声的效果图；

图6是本发明一种基于剪切波的双重图像去噪方法去除图像噪声的效果图。

具体实施方式

下面结合附图和具体实施方式对本发明进行详细说明。

一种基于剪切波的双重图像去噪方法，如图1所示，包括以下步骤：

步骤1、对噪声图像f(x,y)进行分解，得到不同尺度的低频序列和高频序列；

剪切波变换是对小波变换的继承和发展，它克服了小波变换的方向局限性和平移不变性的缺陷，其实现过程更加灵活有效。剪切波变换结合了小波的多尺度特点，能根据方向进行剖分，它构造简单，通过对函数进行伸缩、平移、旋转操作生成基函数，表达式为：

式中：为剪切波的生成函数，a∈r⁺为刻度参数函数，s∈r为剪切波变量，t∈r为平移变量，a和b为二阶可逆方阵，其中a为多向异性膨胀方阵，b是剪切方阵。

进一步的，如图2所示，采用剪切波变换对噪声图像f(x,y)进行分解，得到水平和竖直方向低频序列ll(体现图像的主体轮廓)、水平低频和竖直高频序列lh、水平高频和竖直高频序列hl、水平高频和竖直高频序列hh，三个高频序列反映图像的细节边缘，包含着大量的噪声。

步骤2、分别对低频序列、高频序列进行去噪处理；

采用中值滤波对低频序列ll进行去噪处理，得到低频序列

具体原理为：在低频序列中选择奇数像素的窗口，将窗口内的像素按照灰度值排序，以中间位置像素的灰度值代替图像f(x,y)像素点的灰度值，作为窗口的灰度值g(x,y)：

g(x,y)＝median{f(x-k,y-l),(k,l∈m}(3)；

上式中，m为窗口大小；本实施例中选择m＝5的窗口，对低频序列ll进行去噪，经过中值滤波去噪后的低频系数为

中值滤波的输出像素是由邻域像素的中间值决定，而且中值滤波产生的模数较少，更适合消除低频序列的孤立噪声点，同时又能保持图像的细节。

自适应阈值法去噪的思想不是计算全局图像的阈值，而是根据图像不同区域亮度分布，计算其局部阈值，所以对于图像不同区域，能够自适应计算不同的阈值，因此被称为自适应阈值法。采用自适应阈值t分别对高频序列lh、hl、hh进行去噪处理：

得到高频序列

其中，自适应阈值t的表达式为：

式中l是调节因子，为噪声的方差，通过稳健中值法进行估计得到：

σx服从高斯分布的前提下有：

式中n为高频序列的长度，由于故可得到图像f(x,y)的方差估计值：

步骤3、将经步骤2处理后的低频序列、高频序列进行逆变换，得到一重去噪后的图像f1，重构图像的对比度得到了很大改善，大部分噪声也能够被滤除。

步骤4、采用维纳滤波对图像f1进行二重去噪，得到图像f2；

维纳滤波通常用于提取被噪声污染的图像，它是以最小均方误差准则进行滤波的，维纳滤波的主要思想分为三步：滤波、预测和平滑；滤波是利用直到当前时刻的随机过程的观测值，来得到当前信号的估计值；预测是利用直到当前时刻的随机过程的观测值，得到将来某个时刻信号的估计值；平滑是利用直到当前时刻的随机过程的观测值，得到过去某个时刻的估计值。具体原理如下：

如图3所示，将图像f1作为输入图像x(n)，则x(n)＝s(n)+v(n)，s(n)表示无噪图像，v(n)表示噪声；对输入图像x(n)进行维纳滤波后输出y(n)，即为图像f2，输出y(n)无限接近s(n)，为期望值，则误差为：

均方误差为：

j＝e[e²(n)](10)；

则均方误差j最小时滤波器系数为最优解。

分别对小波阈值去噪法、维纳滤波方法及本发明的去燥方法进行试验，去噪效果如下：

采用小波阈值去噪法虽然对噪声有一定的抑制效果，但会使图像变得模糊，低频成分通过，高频边缘细节则被滤去，见图4；维纳滤波方法保留图像结构信息，但去噪效果不太理想，存在残留噪声，见图5；本发明的去燥方法不仅能很好地抑制相关噪声，而且最大限度地保护去噪后图像的边缘信息，图像也较为清晰，取得更好的去噪效果，见图6。

表1为上述三种方法的去噪结果评价指标，峰值信噪比值与去噪效果成正比，值越大表明去噪效果越好，从表1可看出本发明去燥方法的峰值信噪比最高。

通过以上方式，本发明的基于剪切波的双重图像去噪方法，采用剪切波多尺度变换分解，克服小波分解不够精细的缺点，能够更好的对弱小信号进行区分，使该变换具有平移不变性和稳定性等优点；特别是对于弱小目标检测，不会因为下采样操作而导致目标信息丢失；对三个高频序列采用自适应阈值法进行去噪处理，能够更好的消除图像中大部分的噪声，保持图像的边缘；对低频序列系数采用中值滤波去噪，能够消除图像中的孤立噪声，更好的维持图像的清晰度；对重构图像f1采用维纳滤波进行二重去噪处理，能更好的处理图像中的高斯噪声和乘性噪声,清除图像中的残留噪声，使图像变得更平滑，能保持图像的纹理结构等信息。