光机热耦合中非线性拟合方法与流程

本发明涉及工业仿真领域，尤其是涉及光机热联合仿真领域，特别是涉及一种光机热耦合中非线性拟合方法。

背景技术：

在复杂环境中，典型的光机热耦合分析的温度场可以影响表面位移、折射率，进而影响光学镜头的性能，结构载荷以及结构自身的重力载荷也会影响表面位移。一般位移、温度影响和应力影响都会最终拟合成多项式的形式输入为光学面型结果。

传统的光机热耦合分析流程中的多项式拟合过程，一般采用最小二乘法实现，通过逆矩阵的形式实现。

xa＝y

其中a是多项式系数矩阵，x是项样本点矩阵，y是位移或光程差矩阵，则系数矩阵a为

a＝x^-1y

传统的多项式拟合过程只考虑面型位移结果的影响，并没有考虑位移结果本身所在位置的影响，如果样本点选取的不合理、不考虑权重会造成求解的系数误差较大，从而导致对光机结果评价出错，甚至导致设计的重大问题。

技术实现要素：

本发明针对现有技术存在的问题和不足，提供一种光机热耦合中非线性拟合方法。

本发明是通过下述技术方案来解决上述技术问题的：

本发明提供一种光机热耦合中非线性拟合的方法，其特点在于，其包括以下步骤：

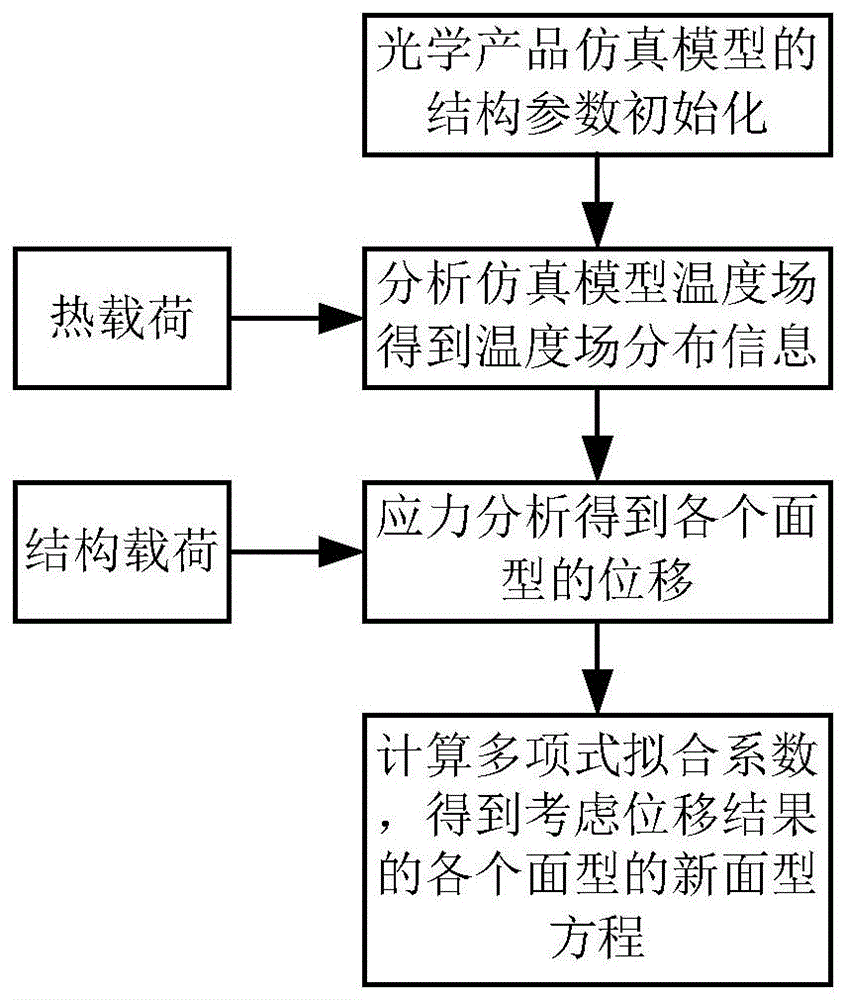
s1、对光学产品的光学产品仿真模型的结构参数进行初始化；

s2、将热载荷加载至光学产品仿真模型中，对光学产品仿真模型的温度场进行分析以得到温度场分布信息；

s3、将结构载荷和温度场分布信息加载至光学产品仿真模型中，对光学产品仿真模型的应力进行分析，从而得到光学产品仿真模型的各个面型的原始面型方程

其中，z表示面型的z轴坐标，x表示面型的x轴坐标，y表示面型的y轴坐标，k表示二次标准曲面系数；

s4、由于原始面型发生位移，则新的面型方程为

将新的面型方程写成多项式的形式

为了求解多形式系数cm，则构造误差函数e

其中，e表示各个面型的误差函数，赋值为零，n表示该面型具有的位移点总数，wi表示该面型的第i个位移点归一化后的权重值，dsi为该面型的第i个位移点的位移值，m表示拟合多项式的项数，表示拟合多项式，cm表示第i个位移点对应的拟合多项式中第m项拟合系数，zm表示第i个位移点对应的拟合多项式中第m项的拟合函数，λ表示权重因子，i表示对角矩阵；

则多项式拟合系数矩阵c为：

c＝(z^tz)^-1z^tswn(4)

其中，c是cm的矩阵形式，z是的矩阵形式，z^t是z的共轭转置，swn是widsi的矩阵形式；

利用公式(4)计算出多项式拟合系数，从而得到考虑位移结果的光学产品仿真模型的各个面型的新的面型方程。

较佳地，利用每个面型的各个位移点及其相邻的两个点或多个点构成的三角形或多边形组成的面积s作为该位移点的权重，并对该位移点的权重进行归一化：

其中si表示某一面型的第i个位移点的权重值，wi表示该面型的第i个位移点归一化后的权重值。

在符合本领域常识的基础上，上述各优选条件，可任意组合，即得本发明各较佳实例。

本发明的积极进步效果在于：

本发明通过把非线性多项式拟合引入到光机热耦合分析，从而避免了离散点不均匀的情况下的计算误差以及离散点误差引起的系数求解误差。

附图说明

图1为本发明较佳实施例的光机热耦合中非线性拟合的方法的流程图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。

如图1所示，本实施例提供一种光机热耦合中非线性拟合的方法，其包括以下步骤：

s1、对光学产品的光学产品仿真模型的结构参数进行初始化。

s2、将热载荷加载至光学产品仿真模型中，对光学产品仿真模型的温度场进行分析以得到温度场分布信息。

s3、将结构载荷和温度场分布信息加载至光学产品仿真模型中，对光学产品仿真模型的应力进行分析，从而得到光学产品仿真模型的各个面型的原始面型方程

其中，z表示面型的z轴坐标，x表示面型的x轴坐标，y表示面型的y轴坐标，k表示二次标准曲面系数。

s4、由于原始面型发生位移，则新的面型方程为

将新的面型方程写成多项式的形式

为了求解多形式系数cm，则构造误差函数e

其中，e表示各个面型的误差函数，赋值为零，n表示该面型具有的位移点总数，wi表示该面型的第i个位移点归一化后的权重值，dsi为该面型的第i个位移点的位移值，m表示拟合多项式的项数，表示拟合多项式，cm表示第i个位移点对应的拟合多项式中第m项拟合系数，zm表示第i个位移点对应的拟合多项式中第m项的拟合函数，λ表示权重因子，i表示对角矩阵。

利用每个面型的各个位移点及其相邻的两个点或多个点构成的三角形或多边形组成的面积s作为该位移点的权重，并对该位移点的权重进行归一化：

其中si表示某一面型的第i个位移点的权重值，wi表示该面型的第i个位移点归一化后的权重值。

则多项式拟合系数矩阵c为：

c＝(z^tz)^-1z^tswn(4)

其中，c是cm的矩阵形式，z是的矩阵形式，z^t是z的共轭转置，swn是widsi的矩阵形式。

利用公式(4)计算出多项式拟合系数，从而得到考虑位移结果的光学产品仿真模型的各个面型的新的面型方程。

本发明解决光机热拟合过程中的多项式拟合，从而实现光机热联合仿真，可以被广泛用于光学工业产品设计初期。

虽然以上描述了本发明的具体实施方式，但是本领域的技术人员应当理解，这些仅是举例说明，本发明的保护范围是由所附权利要求书限定的。本领域的技术人员在不背离本发明的原理和实质的前提下，可以对这些实施方式做出多种变更或修改，但这些变更和修改均落入本发明的保护范围。