一种非线性充电车辆路径优化方法与流程

本发明涉及配送路径优化领域，具体涉及一种非线性充电车辆路径优化方法。

背景技术：

随着经济的快速发展，交通物流产业也随之快速发展。但是随之而来带来了严重的环境问题和资源问题。为了解决这些问题，电动汽车取代传统燃油汽车的现象变得越来越普遍。电池和充电技术的发展也促进了电动汽车的快速发展，加快推进电动汽车充电基础设施建设工作，从而更好的促进了电动汽车的普及。在物流的配送过程中，使用电动汽车进行配送，不仅可以保护环境，而且可以有效的降低能源的消耗。

近年来，车辆路径问题(vehicleroutingproblem，vrp)自从由dantzig和ramser于1959年首次提出以后，已经得到了广泛的研究。目前，关于vrp的研究的比较热门的是带时间窗的vrp(vehicleroutingproblemwithtimewindows，vrptw)，它是在满足客户时间窗和车辆容量约束的前提下，一组车辆能够从仓库出发，以最低的成本为地理上分散的一些客户提供服务，最终返回到仓库的过程。vrptw通常是一个np-hard问题。因此，人们提出了多种启发式算法来解决这类问题。solomon(1987)考虑了用于解决vrp的启发式算法，其中插入启发式显示出优异的性能。其后，针对这类复杂优化问题提出了多种算法，如禁忌搜索算法(tabusearch，ts)，分支定界算法(branch-and-pricealgorithm)，局部搜索算法(localsearch，ls)，大邻域搜索算法(largeneighborhoodsearch，lns)以及迭代局部搜索算法(iteratedlocalsearch，ils)。

此外，在全球节能环保的大背景下，电动汽车(electricvehicles，evs)也逐渐与vrp相结合。一些学者试图将vrp与环境概念结合起来，bektas和gilbert(2011)提出了污染路径问题(pollution-routingproblem，prp)，其中考虑了温室气体的排放、燃料、旅行总时间的成本。和miller-hooks(2012)提出了绿色车辆路径问题(greenvehicleroutingproblems，gvrp)，可以利用可替代燃料站(alternativefuelstations，afs)来克服车辆服务范围有限的问题。bruglieri等人(2019)提出了基于路径的算法来求解gvrp，zhang等人(2018)提出了利用蚁群算法(antcolony，ac)来减少电动汽车能耗问题。然而，除非在沿途中设有充电站，否则电动汽车不能提供太长的路线。总之，电动车辆路径问题(electricvehicleroutingproblem，evrp)有两个核心问题：一个是如何确定充电站的位置，另一个是如何为电动汽车进行充电。

为了使evrp更接近现实，许多学者试图选择充电站的位置。adderly等人(2018)提出了一些措施，比如：增加主干线的充电站数目，以应付自然灾害等紧急情况。breunig等人(2019)提出了两级式的evrp，该方案使用动态规划(dynamicprogramming，dp)来获得两级线路上充电站的最佳位置。大量的文献对于如何对电动汽车进行充电的问题进行了大量的深入研究。desaulniers等人(2016)提出了减少电动汽车的充电容量但是增加充电次数，实验结果显示比完全充电要好。keskin和bülent(2018)提出了三种不同类型的充电站来解决线路上的充电问题，即正常、快速和超快速充电方式的充电站。等人(2012)描述了电流、电压以及充电电平随时间变化的典型曲线。大多数学者将充电过程假设为一个线性充电的过程。然而，在现实生活中，充电过程实际上是一个随时间变化的非线性充电过程，其中有很少一部分学者假设为非线性的充电过程。与线性充电约束的evrp相比，非线性充电约束的evrp应该得到更多的研究。

此外，在最近几年中，很多学者已经提出了许多类型的启发式算范来解决现实的优化问题。比如：人工蜂群算法(artificialbeecolony，abc)，禁忌搜索算法(tabusearch，ts)，遗传算法(geneticalgorithm，ga)以及差分进化算法(differentialevolution，de)。在这些启发式算法中，差分进化算法被认为是一种简单、可靠、健壮且基于种群的算法，它利用当前种群之间的差异来搜索全局最优解。许多学者已经利用差分进化算法来解决许多类型的优化问题，例如社会学习，连续空间上的全局数值优化问题，并行机调度问题，安排原料奶运输问题，光合色素的线性光学响应，多目标的旅行商问题(travelingsalesmanproblem,tsp)，模糊需求和同时提货和送货的车辆路径问题，需求不确定的开放车辆路径问题，有容量限制的车辆路径问题，多目标车辆路径问题，数据驱动的车辆路径分析。基于以上对于差分进化算法的文献研究，已经验证了它是一种具有高效搜索能力，但是很少有人将差分进化算法应用于求解电动车辆路径问题。因此，在本发明中我们提出了一种改进的差分进化算法(improveddifferentialevolution,ide)来求解带时间窗和非线性约束的求解电动车辆路径问题。

综合分析上述文献可见，国内外学者对vrptw模型的构建和算法求解进行了大量的研究，电动车辆在服务的过程中，由于电量消耗而充电的过程可以vrptw为基础建立模型并进行求解，但目前还缺乏相关文献，亟待设计算法进行求解。本发明采用改进的差分进化算法，针对带时间窗和非线性充电约束的电动车辆路径优化问题，以vrptw为基础建立模型并进行求解。

技术实现要素：

本发明的目的在于提供一种带时间窗和非线性约束的电动车辆路径优化方法，以提高配送效率，降低配送成本，解决背景技术中存在的难题。

为实现上述发明目的，本发明所采用的技术方案是：一种非线性充电车辆路径优化方法，所述方法包括以下步骤：

s1:依据电动车辆的车型问题，扩充现有solomon算例中的参数并读取算例的任务；

s2：确定配送路径优化的目标及约束条件；

s3：提出一种等级评定的方式确定客户满意度；

s4：采用改进的差分进化算法优化路径解决方案；

s5：提出一种充电量调整策略来优化路径解决方案；

s6：提出一种负电量修复策略来优化路径解决方案；

s7：将所述路径优化方案下发到各个配送车辆。

优选的，所述s1中，在现有的solomon算例中扩充的参数包括：

包括v个客户，某个客户i，另一个客户j，i＝1～v中任一自然数，j＝1～v中任一自然数，i≠j；

包括f个充电站，某一个充电站y，y＝1～f中任一自然数；

包括k个车辆，某个车辆k，k＝1～k中任一自然数；

包括xij，xij为约束变量，如果车辆能够从客户i到客户j,则这个值为1，否则为0；

包括di，di表示客户i对货物的需求量。

优选的，所述s2中确定优化的目标为f：

式(1)中α是旅行时间的权重，α≥0，β是客户满意度的权重，β≥0，α+β＝1；tij是车辆从客户i到客户j所花费的时间；△y是车辆在充电站点y的充电时间；γ是目标系数；svi是客户i所对应的客户满意度等级；

所述s2中约束条件为：

车辆k的总派送时长不能超过车辆最大工作时长tmax；

其中总派送时长包括派送路途耗费时间tij、客户的服务时间si和车辆在充电站的充电时间△y；

每个客户只能由一辆车进行服务，每辆车的负载不能超过其最大负载；

提供服务的车辆必须在配送中心开始和结束，同时该车辆在配送中心时前面和后面的节点均不超过一个。

优选的，所述s3是这样实现的：

当服务车辆在ti时到达客户i有三种情况:

第一种：当服务车辆在严格时间窗内到达并服务，即eti≤ti≤lti时，客户满意度svi＝1；

第二种：当服务车辆在提前松弛时间窗内到达，即eeti≤ti≤eti时，客户满意度

第三种：当客服务车辆在延迟松弛时间窗内到达，即lti≤ti≤llti时，客户满意度

[eti，lti]为客户i的严格时间窗，[eeti，llti]为户客户i的松弛时间窗。

优选的，所述s4是这样实现的：

步骤1按照扩充的solomon算例，循环生成x＝(x¹,x²,...,x^m)共m个初始解存入当前解集；

步骤2变异操作；

步骤3交叉操作；

步骤4选择操作。

优选的，所述s4中步骤1是这样实现的：

按照扩充的solomon算例，利用改进的pfih策略(ipfih)，循环生成pn-1个初始解，再利用pfih策略生成一个初始解，初始解存入当前解集；首先，在不考虑电池容量的情况下分配客户，然后再在解决方案考虑加入电池容量因素；由于有些车辆到达客户时，电池容量可能为负数；因此，需要考虑插入充电站进行充电操作，所述步骤1的编码策略如下：

采用两个二维数组的方式编码一个解，即车辆分配数组和充电操作数组；第一个二维数组的第一维表示每一辆车，对于每辆车创建一个数组，包含该车辆服务的客户点序列，客户点序号的先后顺序表示这些客户点的服务次序；第二个二维数组的第一维表示每一辆车，对于每辆车创建一个数组，包含该车辆服务的过程中进行充电的充电站次序；

具体的充电站初始化策略步骤如下：

步骤a：在插入充电站之前，首先得到车辆到达客户时电池容量为负的情况和当前旅行时间的总和；

步骤b：如果车辆的电池容量为负时，则有必要尝试插入充电站进行充电，以获得最佳解决方案，尝试在每个位置插入每个充电站；

步骤c：在车辆进行充电后，重新计算总的旅行时间和总的到达客户的电池容量为负的情况；

步骤d：记录插入每个充电站后路线的情况；

步骤e：测试完所有位置的所有充电站后，选择最佳充电站和最佳位置进行真正的插入。

优选的，所述s4步骤2中变异操作中当前解xⁱ的产生策略i：

步骤a:为了生成邻域解，随机选择一辆车，然后从中随机选择一个客户，并将其在所选车辆中删除；

步骤b：将所选客户插入到另一辆车中；

或

变异操作中当前解xⁱ的产生策略ii：

步骤a：为了生成邻域解，与策略i相同，随机选择一辆车，然后从所选车辆中随机选择一定数量的客户并将这些客户从当前车辆中删除；

步骤b：将选择的客户随机插入到其他车辆中。

优选的，所述s4中步骤3交叉操作具体步骤如下：

步骤①：选择当前解xⁱ，然后再选择最优解x^best，将两部分组合起来；

步骤②：从当前解xⁱ中随机选择一辆车，再从最好解x^best中找到该车辆所服务的客户；

步骤③：从最好解中删除这些相应的客户；

步骤④:将这些被删除的客户插入到最好解x^best中的其他车辆。

优选的，所述s5是这样实现的，在当前的策略中，电池容量每次都充满电，但为最后一个客户提供完服务返回仓库时仍然有剩余的电池容量；从环保的理念来看，在充电过程中降低电池容量是必要的；根据最后返回到仓库时的剩余电池容量，在充电过程中调整在充电站的充电量，然后根据非线性充电函数计算充电时间，从而减少总的旅行时间；

对于调整在充电站的充电容量应满足以下条件：

(1)如果路线上只有一个充电站，应确保在当前充电站充电后，车辆以零电池容量返回仓库；

(2)如果路线上有两个或两个以上充电站，确保从当前充电站到下一个充电站的电池容量为0；

具体步骤如下：

步骤甲：循环每个车辆，查看是否有充电桩，如果有，则查看有几个，并且记录每个车辆，充电桩的插入位置；

步骤乙：对于每个车辆，倒推充电量，并修改每辆车的每个客户点的剩余电量；

步骤丙：返回在充电站合适的充电值。

优选的，所述s6是这样实现的：

在变异或交叉操作后，到达一些客户点的电池容量会出现为负的情况，当前解变成不可行解；因此，本发明提出了一种负电量修复策略，考虑了两种策略：

策略①：

为了产生可行解，可以把这些负电平的客户点删除，另增加一个车辆服务这些客户点；

或

策略②：

除了策略i中产生可行解，把这些负电平的客户点删除，插入到其他车辆，但这里有一个难题，其他车辆已经按照到达最后一位客户提供了服务，并返回到仓库，已经充电量调整策略设置了，所以很难插入其他车辆；因此，添加其他车辆来服务这些客户是困难的；为了满足这个条件，本发明提出可以增加在充电站的充电量，使之有可能为这些客户点提供服务。

本发明的有益效果集中体现在：能够提高配送效率，降低配送成本。

附图说明

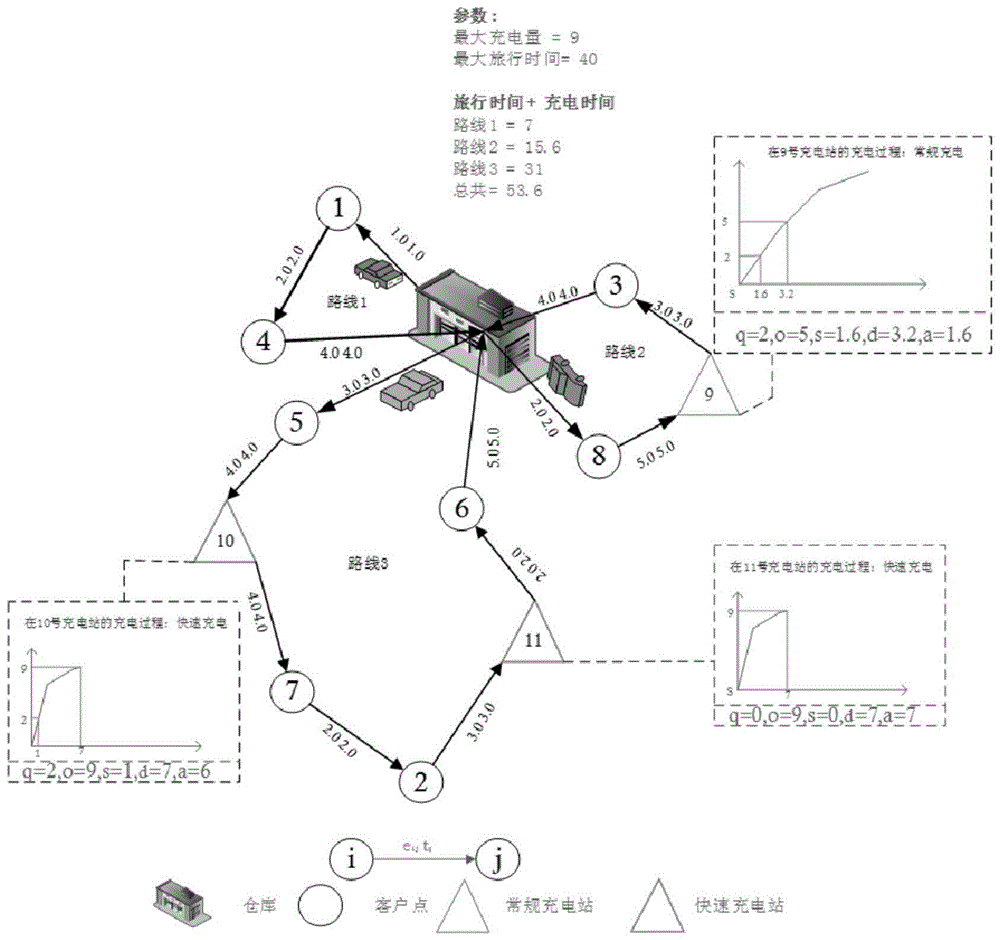
图1为本发明带时间窗和非线性充电的电动车辆路径优化问题的例图。

图2为solomn经典算例场景图。

图3为本发明方法中的编码示意图。

图4为本发明方法中的解码示意图。

图5为本发明中的客户满意度等级函数示意图。

图6为本发明中的充电站插入策略示意图。

图7为本发明中当前解xⁱ的产生策略ii示意图。

图8为本发明中交叉策略示意图。

图9为本发明中负电量修复策略示意图。

图10为本发明中two-phasega、itsa和ide算例比较收敛曲线示意图。

图11为本发明方法中算例的客户点服务时间gantt图。

具体实施方式

下方将结合实施例对本发明进行完整的阐述：

下面结合附图对本发明做进一步详细描述：

本发明提出了一种带时间窗和非线性充电约束的电动车辆路径优化问题的差分进化算法。结合问题特征，算法采用一种改进的差分进化算法。算法分为初始化、变异、交叉和选择四个阶段。改进的差分进化算法阶段中的变异策略与交叉策略，从而提高了种群数量，增大了找到更优解的概率。同时还提出了一种充电量调整策略和负电量修复策略来进行优化，可以有效的提高解的质量。实验结果验证了所提出的改进的差分进化算法的有效性。同时采用了一种满意度等级策略更贴合实际，具有应用价值。

1、带时间窗和非线性充电约束的电动车辆路径优化问题描述。

在本发明中，将问题定义为带时间窗的evrp的扩展，该问题的特征可以概括为：(1)所有的电动汽车的类型都是同类型的；(2)电动车辆的电池容量应该始终保持非负的状态；(3)每个客户都有一个时间窗约束和服务时间；(4)车辆的充电过程是一个非线性的充电过程；(5)每个充电站的充电过程分为四个不同的充电速度。

在现实的物流配送系统中，充电过程是一个随时间变化的非线性充电过程。大多数的研究中假定电动汽车从仓库是以充满的状态开始提供服务的，并且所有充电站都可以同时处理无限数量的电动汽车，不需要等待。从利益的角度来看，电动汽车在夜晚充电是更有利。同时，在激烈的市场竞争下，在物流配送过程中必须重视客户满意度，这通常有利于提高配送效率。例如，在客户的时间窗口内到达的车辆将达到更高的满意度。因此，本发明使用服务等级来定义客户满意度。只要有提前或延迟，就会导致满意度等级下降。

此外，计算客户满意度的方式可以分为两类：一种是基于客户数量，这取决于提前或延迟提供服务的客户数量占总客户的比例。另外一种是利用时间窗来计算满意度。当时间窗是硬窗口时，则顾客满意度值为0或1；当时间窗是模糊时间窗或者是软时间窗，则利用三角模糊隶属函数来描述客户的满意度。本发明采用服务等级的方法来确定客户满意度，这与其他文献中的研究不同，在其他研究中，利用了超出时间窗口的客户数量添加到目标值中，这些不能够反映出短时间窗口内客户的紧迫性。本发明的计算客户满意度的方式有许多优点：第一，客户越重要，则时间窗就越紧；第二，这个比例是由相对于时间间隔早或晚计算出来的来表示客户满意度，并将该服务等级整合到目标函数中。这些优点有助于使研究的问题更加具有现实性。

因此，在本发明中，有以下假设：

(1)每条路线必须在仓库开始和结束；

(2)总的服务客户的需求之和不能超过所提供服务车辆的最大容量；

(3)每名客户必须只由一辆电动汽车提供服务；

(4)每个客户都有一个时间窗约束和服务时间；

(5)每条路线均要考虑最长的行车时间限制，且不能超过这个最大极限；

(6)电动汽车的电池容量一直保持非负的状态；

(7)电动汽车的充电过程是一个非线性的充电过程；

(8)目标是最小化总出行时间和客户满意度的加权总和。

当任何电动汽车到达充电站时，它都会根据电动汽车所剩余的电量根据充电函数来选择一个充电级别，进而影响充电时间，从而影响整个目标值。在图1中给出了描述这个问题的典型例子。在图中有8个客户和3个充电站。充电站有两种类型(常规和快速充电)。利用充电站所对应的分段线性函数将电池容量q和o映射到充电时间s到d，从而估计在充电站所充电的时间，并用a表示了s与d之间的时间差。在这个例子中，路线1不需要访问任何充电站。路线2在9号充电站进行充电，电动汽车以零电量到达充电站。并将电池容量充电至o＝5的电量，进而借助于分段线性函数来估计充电时间，因此，路线2消耗15.6个时间单位，其中总旅行时间为14个时间单位，充电时间为1.6个时间单位。最后，路线3分别消耗了2个和6个充电时间单位。

1.1带时间窗和非线性充电约束的电动车辆路径优化问题建模

参数和符号表示如下：

目标函数(1)是最小化两个目标的加权和，其中第一项是总旅行时间，包括行程时间和充电时间，第二项是客户满意度。约束(2)是确保每个客户只服务一次。约束(3)定义每个充电站的充电次数。约束(4)是电动汽车从仓库出发时是充满电的状态。约束(5)是对电动汽车到达和离开充电站时电池容量的限制，确保电池容量一直是非负的，且不超过最大电池容量。约束(6)表示tsi与tdi之间的时间差，即在充电站进行充电的时间。约束(7)是确保电动汽车的电池容量始终是非负的状态，并且电池的容量可以到达下一个点。约束(8)表示两个相邻客户之间的时间关系。约束(9)是车辆到达客户点的时间窗不能超过松弛时间窗限制。约束(10)确保总出行时间之和不超过最大旅行时间限制。约束(11)定义权值的约束条件。

1.2带时间窗和非线性充电约束的电动车辆路径优化问题算例

经典的vrptw算例，如solomon算例，包括56个算例，每个算例中包含100个客户点，客户点的布局分为三大类，即17个聚合程度较高的c(clustering)系列算例、23个聚合程度分散的r(random)系列算例和16个聚合程度处于中间状态的rc系列。图2展示了两种不同场景的客户点分布图。c系列算例的主要特点包括：(1)客户点聚合程度较高，多个客户点形成一簇；(2)客户点的需求量相对较大，因而车辆只能配送有限客户；(3)客户点的时间窗长度相对较大。r系列算例的主要特点包括：(1)客户点分散程度较高；(2)客户点的需求量很小，因而车辆能配送足够多的客户点；(3)客户点的时间窗长度相对较小。上述特点决定了不同结构的vrptw问题有不同的问题特性，因而应该采用不同的启发式规则进行求解。solomon经典算例场景图如图2所示。

经典solomon算例，没有对于充电站的设置，同时也没有注明车辆每单位的消耗率，为了更好地考虑实际约束，本发明在solomon经典算例的基础之上，增加了充电站的位置以及车辆每单位的消耗率。利用聚类的方法来生成充电站的位置，通过计算每个客户之间的距离，将solomon算例的100个客户划分为多个类。然后，通过计算属于同一类的客户坐标的平均值，从而为每个类设计充电站的位置。

扩展的经典solomon算例，包括55个算例，每个算例中包含100个客户点，客户点的布局分为仍然分为三大类，即聚合程度较高的c(clustering)系列算例、聚合程度分散的r(random)系列算例和聚合程度处于中间状态的rc系列。

2求解带时间窗和非线性充电约束的电动车辆路径优化算法

2.1差分进化算法

差分进化(differentialevolution，de)算法是storn和price在1995年提出的。在基本的差分进化算法中，需要迭代执行变异、交叉等几个操作，从而可以实现开发和探索任务。差分进化算法的关键过程描述如下：

(1)编码和初始化种群

对于连续优化问题，每个解都用基本的de中的实数表示。需要注意的是，每个解决方案中的元素必须xij^(l)和xij^(u)之间的范围内。

xij(0)＝xij(l)+rnd[0,1]·(xij(u)-xij^(l))；i＝1,...,d.j＝1,....np

其中rnd[0,1]表示在该范围内随机生成的数字。

(2)变异操作

变异作为差分进化的核心操作，在差分进化的搜索过程中起着至关重要的作用。变异操作符使用以下公式：

vij(t+1)^g+1＝xic(t)^g+f*[xia(t)^g-xib(t)^g](12)

其中a,b,c∈[1,np]，并且彼此是不同的，即a≠b≠c≠j，f是缩放因子，xia(t)^g-xib(t)^g是差化向量。

(1)交叉操作

为了增加潜在的多样性，在变异操作之后执行交叉操作。交叉操作由以下等式定义：

其中randn(i)，randn(i)是[1,n]中的随机整数，g表示当前迭代的次数，cr∈[0,1]是交叉概率。

()估计和选择操作

为了确定vij(t+1)^g+1是否是下一代，下面给出了估计和选择操作符，以保证将较好的适应值被保留：

重复步骤(2)至(4)，直到迭代次数达到最大值为止。需要注意的是：这个准则是通过贪婪来选择实现的。

2.2问题编码

在这一部分中，考虑到问题的约束条件，本发明利用两个二维数组的方式编码一个解，即车辆分配数组和充电操作数组，采用两个二维数组的方式编码一个解，即车辆分配数组和充电操作数组。第一个二维数组的第一维表示每一辆车，对于每辆车创建一个数组，包含该车辆服务的客户点序列，客户点序号的先后顺序表示这些客户点的服务次序。第二个二维数组的第一维表示每一辆车，对于每辆车创建一个数组，包含该车辆服务的过程中进行充电的充电站次序。图3(a)给出了车辆分配数组的说明性示例，其中第一维表示所有车辆，第二维度表示每个车辆所服务的客户。例如，有三辆车：第一辆车服务于三个客户{5，1，2}，另外两辆车分别服务于{4，7}和{6，8，3，9}。

图3(b)说明车辆是否在每个充电站充电，如果车辆在相应的充电站充电，则将元素设置为充电站编号，否则设置为“-1”。例如，第一辆车将在编号为0的充电站进行充电，并且它没有访问其他充电站。第二辆车将在2号充电站进行充电，而最后一辆车将分别在3号和4号充电站进行充电。

2.3问题解码

在解码过程中，借助于上面提到的两个二维数组，可以找到车辆经过的整条路径。首先利用充电操作数组来判断车辆是否在充电站充值，然后结合车辆分配数组来确定客户之间或客户与仓库之间进行了充电操作，最终找到车辆经过的整条路径。在图4中，两个客户{5，2}由ev_a提供服务，第二序列{-1，-1，0，-1}表示ev_a将在编号为“0”的充电站进行充电。由此可以看出，充电操作是发生在编号为2和5的客户之间，因此ev_a的整个路线表示为{0，5，‘0’，2，0}

2.4客户满意度的计算

近几年来，顾客满意度水平得到了越来越多的研究关注，因为顾客满意度水平往往代表着服务绩效。计算客户满意度值的常用方法是直接将其添加到目标值中。譬如，afshar-bakeshloo(2016)提出，在严格时间窗和松弛时间窗之间，顾客满意度值被认为是线性函数。然而，在现实的实际应用中，客户通常不能给出每个时间点的精确值。例如，在调度物流中，客户通常会给出几级服务满意度的值，这可以看作是一个分段函数。图5描述了这种分段函数的示例。

本发明对于客户满意度的计算的具体步骤如下：

当服务车辆在ti时到达客户i时有三种情况:

第一种：当服务车辆在严格时间窗到达并服务，即eti≤ti≤lti时，客户满意度svi＝1；

第二种：当服务车辆在提前松弛时间窗到达，即eeti≤ti≤eti时，客户满意度

第三种：当客服务车辆在延迟松弛时间窗内到达，即lti≤ti≤llti时，客户满意度

2.5充电站的初始化策略

首先，在不考虑电池容量的情况下分配客户，然后再在解决方案考虑加入电池容量因素。由于有些车辆到达客户时，电池容量可能为负数。因此，需要考虑插入充电站进行充电操作。图6描述了在路线中插入充电站的过程。

为了更好地描述插入充电站的过程，其具体步骤如下：

步骤1：在插入充电站之前，首先得到车辆到达客户时电池容量为负的情况和当前旅行时间的总和；

步骤2：如果车辆的电池容量为负时，则有必要尝试插入充电站进行充电，以获得最佳解决方案，尝试在每个位置插入每个充电站；

步骤3：在车辆进行充电后，重新计算总的旅行时间和总的到达客户的电池容量为负的情况；

步骤4：记录插入每个充电站后路线的情况；

步骤5：测试完所有位置的所有充电站后，选择最佳充电站和最佳位置进行真正的插入。

2.6改进的变异操作：

变异操作中当前解xⁱ的产生策略i：

步骤1：为了生成邻域解，随机选择一辆车，然后从中随机选择一个客户，并将其在所选车辆中删除；

步骤2：将所选客户插入到另一辆车中。

变异操作中当前解xⁱ的产生策略ii(图7)：

步骤1：为了生成邻域解，与策略i相同，随机选择一辆车，然后从所选车辆中随机选择一定数量的客户并将这些客户从当前车辆中删除；

步骤2：将选择的客户随机插入到其他车辆中。

2.7改进的交叉操作如下：

交叉策略具体步骤如下(图8)：

步骤1：选择当前解xⁱ，然后再选择最优解x^best，将两部分组合起来；

步骤2：从当前解xⁱ中随机选择一辆车，再从最好解x^best中找到该车辆所服务的客户；

步骤3：从最好解中删除这些相应的客户；

步骤4:，将这些被删除的客户插入到最好解x^best中的其他车辆。

2.8充电量调整策略

在当前的策略中，电池容量每次都充满电，但在为最后一个客户提供完服务返回仓库时仍然有剩余的电池容量。从环保的理念来看，在充电过程中降低充电容量是必要的。因此，本发明提出了一种充电量调整策略。根据最后返回仓库时的剩余电池容量，在充电过程中调整在充电站的充电容量，然后根据非线性充电函数计算充电时间，从而减少总的旅行时间。

对于调整在充电站的充电容量应满足以下条件：

(1)如果路线上只有一个充电站，应确保在当前充电站充电后，车辆以零电池容量返回仓库；

(2)如果路线上有两个或两个以上充电站，确保从当前充电站到下一个充电站的电池容量为0。

具体步骤如下：

步骤1：循环每个车辆，查看是否有充电桩，如果有，则查看有几个，并且记录每个车辆，充电桩的插入位置；

步骤2：对于每个车辆，倒推充电量，并修改每辆车的每个客户点的剩余电量；

步骤3：返回在充电站合适的充电值。

2.9负电量修复策略

在变异或交叉操作后，到达一些客户点的电池容量为负的电池容量，当前解变成不可行解。因此，本发明提出了一种负电量修复策略，考虑了两种策略：

策略i:

为了产生可行解，可以把这些负电平的客户点删除，另增加一个车辆服务这些客户点；

策略ii:

除了策略i中产生可行解，把这些负电平客户点删除，插入到其他车辆，但这里有一个难题，其他车辆已经按照到达最后一位客户提供了服务，并返回到仓库，电池容量为零策略设置了，所以很难插入其他车辆。因此，添加其他车辆来服务这些客户是困难的。为了满足这个条件，可以增加在充电站的充电量，使之有可能为这些客户点提供服务。

图9详细描述这个过程。例如，从编号为10的车辆中删除编号为30的客户。现在，假设插入十个车辆(即编号为0到9的车辆)，编号为7的车辆服务完{1，2，5，7}这些客户，其中在客户编号5和7之间有一个编号为8的充电站，充电过程中电池容量为100。我们可以将该值增加到150，以确保此车辆可以到达编号为7的客户，然后再为编号为30的客户提供服务。则利用负电量修复策略得到的该序列为{1，2，5，7，30}。

3实验结果与分析

3.1仿真实验参数设置

具体包括：(1)种群大小ps，即实验中的个体总数。(2)删除比率dr，决定当前解的车辆上所删除的客户数量。(3)交叉概率pc，即确定每个个体的交叉操作的可能性。

3.2仿真结果分析

为了验证本发明所提改进的差分进化算法(ide)的有效性，本发明选取两阶段遗传算法(two-phasega)和改进的禁忌搜索算法(itsa)作为对比算法，求解了扩展的55个vrptw算例。

表1给出了算法针对55个vrptw算例的实验对比，表中第一列给出了算例名称，第二列给出了每个算法中所有对比算法获得的最好值，接下来三列展示出三种对比算法获得的每个算例的最好目标值，最后三列展示出三种对比算法得到的均方差，计算公式如下：

dev＝(fc-fb)/fb×100％(15)

由表可见，本发明提出的ide算法在求解扩展的vrptw算例中：(1)得到了35个最优解，而由two-phasega和itsa计算的最优解分别有2个和19个；(2)通过均方差15可见，与其他算法相比，ide算法具有显著的有效性。

为了进一步验证所提出的算法在解决这一问题方面的性能，每个算法在同一台计算机上运行了5次，随机选择了6个算例。图10(a)—(f)描述了算例的收敛曲线。

图11描述了算例的客户服务时间和充电时间甘特图，其中每个矩形对应一个客户，数字“v1”表示第一辆车，矩形内的数字表示客户编号。譬如，编号为11的车辆服务的客户序列有{59，58，60，38，39，19，12，100}，客户总数为8，每个客户右边的数字表示客户点结束服务的时间。例如，客户59的最终结束服务的时间为125。需要注意的是：在客户60和38之间的充电站的编号为3。

表1实验结果对比