一种电缆泵送分簇射孔管串井筒通过能力分析方法与流程

本发明涉及一种电缆泵送分簇射孔管串井筒通过能力分析方法。

背景技术：

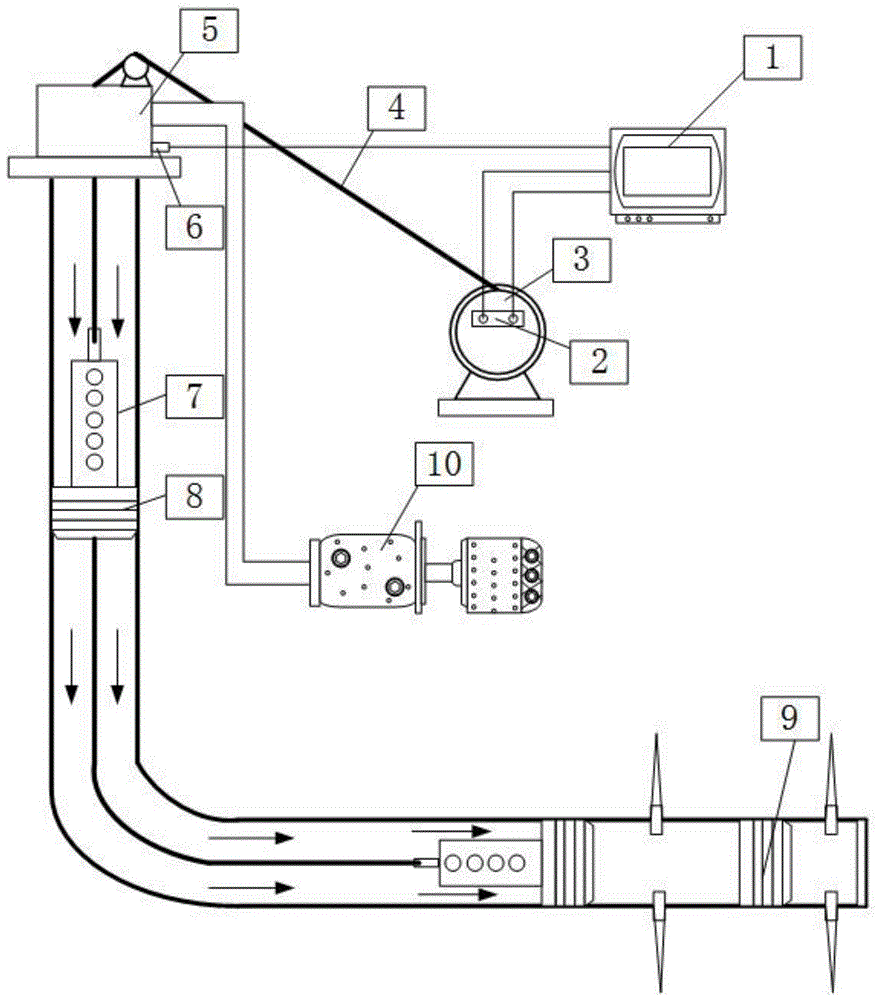
近年来，分簇射孔给国内射孔工艺技术带来了革命性的发展。在分簇射孔作业中，电缆将管串输送到井下目的层，依次完成桥塞坐封和多簇射孔作业，如图1所示。分簇射孔管串作为射孔工具主体，在射孔作业中起着至关重要的作用。分簇射孔管串的长度往往较大，例如，xx202-h1井中“1桥塞+12簇射孔枪”管串长度达到了17.8m，随着簇数增加，管串长度甚至可达20m。在井眼轨迹不规则、狗腿度较大等特殊井况下，射孔管串可能在下井过程中突然遇卡，造成泵送压力的突然升高，导致压裂桥塞提前坐封等事故。这就需要在设计和下入射孔管串之前分析管串在井筒中的通过能力。

关于井下工具通过性的研究，现有研究主要采用几何法和力学法分析。1990年，冉竞提出了刚性条件下井下工具通过能力的计算方法。之后，赵俊平、苏义脑完善了刚性通过性模型，并建立了柔性条件下采用纵横弯曲法求解井下工具通过能力的力学模型。狄勤丰、余志清在此基础上考虑了扶正器对钻具通过性的影响，但是忽略了轴向力的影响。1997年，何世明等通过力学分析，建立了套管在水平井中的摩阻计算模型。随后，眭满仓等在套管摩阻分析中考虑了旋转下入的影响。2008年，王艳红详细论述了井下工具通过性的力学分析方法。2013年，朱秀星等建立了刚性条件下联作管串长度控制方程，由于没考虑管串变形，计算结果偏于保守。2016年，冯定等在假定井眼轨迹最大曲率处为分注管串卡点位置的条件下，对多层分注管串开展了通过性研究。

目前，对于井下工具通过性的计算，相关研究多是以钻具钻杆为例，将井下工具串简化为一受净重横向分力和轴向压力的等截面梁分析模型，并且大多假定工具串在最大狗腿度处遇卡。这些模型对大刚度工具串来说，结果较好。但对于分簇射孔管串之类柔性较大的工具串，这样的简化和假定与实际情况有很大差异，导致预测结果过于保守。

技术实现要素：

本发明的目的在于克服现有技术的缺点，提供一种电缆泵送分簇射孔管串井筒通过性分析方法。

本发明的目的通过以下技术方案来实现：一种电缆泵送分簇射孔管串井筒通过性分析方法，它包括以下步骤：

s1、根据井下电缆泵送分簇射孔工具的结构分析和射孔工艺分析，作出以下假设：假定射孔管串变形为弹性变形；假定分簇射孔管串的材料均匀且各项同性；假定具有相同外径的工具为一段梁；整个分簇射孔管串看作受轴向力和横向分布载荷作用的变截面简支梁；

s2、建立电缆泵送分簇射孔管串井筒通过能力分析模型：

s2(1)、井眼曲率半径的确定：

式中：在井眼轨迹第i段中，δs为测点测深增量；δα为井斜角增量；为方位角增量；ki为全角变化率(狗腿度)；ri为井眼曲率半径。

s2(2)、管串井筒通过条件：

ymax≥yc，可通过(4)

ymax＜yc，不能通过(5)

式中：ymax为管串最大挠度，为了便于计算，认为在管串中点；yc为管串工具中部由于井筒约束而产生的挠曲变形量；db为套管直径；dz为管串中点处外径；dq为桥塞外径；l为管串总长度。

θ＝θ1+θ2≤[θ](6)

式中：θ1、θ2分别为柔性短节左右两端转角；θ为表示柔性短节转角；[θ]为柔性短节许用转角。

s2(3)、分簇射孔管串受力分析

式中：fp为管串轴向分力；fn为管串横向分力；ff为管串所受总阻力；fd为电缆所受摩擦力；fb为泵推力；w、w′分别为管串与电缆在井液中单位长度重量；l′为电缆在斜井段与水平段中的长度；α为井斜角；f为管串、电缆与井筒的摩擦系数；cd为流体阻力系数；vr为管串与井液相对速度；ρm为井液密度；a为管串最大横截面积。

s2(4)、分簇射孔管串变形分析

①根据静力平衡关系可以求得管串两端支反力

②管串任意一点弯矩可用下式表示：

式中：pi(i＝1,n)为第i段轴向拉力，pi＜0，即：

③管串变形挠曲线微分方程：

eiiyi″＝-mi(x)(li-1≤x≤li)(11)

④微分方程的通解如下：

式中：

式(12)确定的管串挠曲线方程与转角方程还可进一步写为：

为求解公式(13)，还必须给出相应的边界条件、连续条件。

边界条件：

y1(0)＝0,yn(ln)＝0(14)

连续条件，即变截面处挠度与转角相等：

s3、电缆泵送分簇射孔管串井筒通过能力分析模型的求解：

把式(14)、(15)和(16)代入式(13)中可得矩阵形式的挠度与转角方程组：

hx＝b(17)

式中：h＝ar+aii，b＝br+bii均为复数。

令sh(k′ilj)＝e′ij，ch(k′ilj)＝f′ij(i,j＝1,n)，式(17)中各项为：

br2n×1＝(b1b2…bi…b2n-1b2n)^t(20)

βι2n×1＝0(21)

x2n×1＝(a1b1…aibi…anbn)(22)

式(20)中：

采取复系数全选主元高斯消去法求解方程组(17)，将得到的(22)式代入方程组(13)，可得受轴向拉力和横向分布载荷作用的变截面简支梁挠度方程与转角方程。在此基础上，可根据挠度方程得到管串在无井壁约束作用下的最大挠度y′max和柔性短节两端转角θ1、θ2。对于有井壁约束的实际情况，当yc＞0且y′max≥yc+(db-dw)时，管串紧贴下端井壁，此时，管串实际最大挠度为：ymax＝yc+(db-dw)。

以上推导针对的是轴向力pi＜0，即受拉的情况。对于水平井，随着管串的下入，井斜角增大，净重轴向分力减小，此时，由于受到阻力或泵推力的作用，管串可能受到轴向压力，即pi＞0，此时，将ki换成下式并代入以上各式可求得受压时的挠度方程。

s4、根据步骤s1～s3计算出的公式分析出分簇射孔管串在井筒中的变形，根据计算出的变形挠度与转角，可评估该管串在井筒中的通过能力。

本发明具有以下优点：通过该分析方法有效提高了电缆泵送分簇射孔效率，避免了管串因突然遇卡而导致泵送压力突然升高与压裂桥塞提前坐封的事故，降低了管串因遇卡而造成其损伤的风险。

附图说明

图1分簇射孔施工过程示意图。1—数据采集及控制系统；2—电缆张力传感器与速度传感器；3—绞车；4—电缆；5—井口密封装置；6—井口压力传感器；7—射孔枪；8—压裂桥塞；9—坐封后桥塞；10—液压泵

图2x206井井眼轨迹示意图；

图3测点与井深对应关系图；

图4井斜角随测点变化示意图；

图5狗腿度随测点变化示意图；

图61桥塞+4簇射孔枪管串结构示意图。图中1—打捞矛1；2—打捞矛2；3—加重1及柔性短节1；4—加重2；5—柔性短节2及cll等；6—射孔枪串；7—桥塞点火头及坐封工具；8—坐封筒及桥塞；

图7不同测点下ymax与yc的变化；

图8管串下入过程中遇卡处挠度；

图9x206井井眼轨迹二维示意图；

图10管串下入过程中柔性短节转角变化；

图11大斜度井段与水平井段不同测点下摩擦力与管串轴向力变化；

图12泵推力随测点变化示意图

具体实施方式

下面结合附图对本发明做进一步的描述，本发明的保护范围不局限于以下所述：

一种电缆泵送分簇射孔管串井筒通过能力分析方法，它包括以下步骤：

s1、根据井下电缆泵送分簇射孔工具的结构分析和射孔工艺分析，作出以下假设：假定射孔管串变形为弹性变形；假定分簇射孔管串的材料均匀且各项同性；假定具有相同外径的工具为一段梁；整个分簇射孔管串看作受轴向力和横向分布载荷作用的变截面简支梁；

s2、建立电缆泵送分簇射孔管串井筒通过能力分析模型：

s2(1)、井眼曲率半径的确定：

式中：在井眼轨迹第i段中，δs为测点测深增量；δα为井斜角增量；为方位角增量；ki为全角变化率(狗腿度)；ri为井眼曲率半径。

s2(2)、管串井筒通过条件：

ymax≥yc，可通过(4)

ymax＜yc，不能通过(5)

式中：ymax为管串最大挠度，为了便于计算，认为在管串中点；yc为管串工具中部由于井筒约束而产生的挠曲变形量；db为套管直径；dz为管串中点处外径；dq为桥塞外径；l为管串总长度。

θ＝θ1+θ2≤[θ](6)

式中：θ1、θ2分别为柔性短节左右两端转角；θ为表示柔性短节转角；[θ]为柔性短节许用转角。

s2(3)、分簇射孔管串受力分析

式中：fp为管串轴向分力；fn为管串横向分力；ff为管串所受总阻力；fd为电缆所受摩擦力；fb为泵推力；w、w′分别为管串与电缆在井液中单位长度重量；l′为电缆在斜井段与水平段中的长度；α为井斜角；f为管串、电缆与井筒的摩擦系数；cd为流体阻力系数；vr为管串与井液相对速度；ρm为井液密度；a为管串最大横截面积。

s2(4)、分簇射孔管串变形分析

⑤根据静力平衡关系可以求得管串两端支反力

⑥管串任意一点弯矩可用下式表示：

式中：pi(i＝1,n)为第i段轴向拉力，pi＜0，即：

⑦管串变形挠曲线微分方程：

eiiyi″＝-mi(x)(li-1≤x≤li)(11)

⑧微分方程的通解如下：

式中：

式(12)确定的管串挠曲线方程与转角方程还可进一步写为：

为求解公式(13)，还必须给出相应的边界条件、连续条件。

边界条件：

y1(0)＝0,yn(ln)＝0(14)

连续条件，即变截面处挠度与转角相等：

s3、电缆泵送分簇射孔管串井筒通过能力分析模型的求解：

把式(14)、(15)和(16)代入式(13)中可得矩阵形式的挠度与转角方程组：

hx＝b(17)

式中：h＝ar+aii，b＝br+bii均为复数。

令sh(k′ilj)＝e′ij，ch(k′ilj)＝f′ij(i,j＝1,n)，式(17)中各项为：

br2n×1＝(b1b2…bi…b2n-1b2n)^t(20)

βι2n×1＝0(21)

x2n×1＝(a1b1…aibi…anbn)(22)

式(20)中：

采取复系数全选主元高斯消去法求解方程组(17)，将得到的(22)式代入方程组(13)，可得受轴向拉力和横向分布载荷作用的变截面简支梁挠度方程与转角方程。在此基础上，可根据挠度方程得到管串在无井壁约束作用下的最大挠度y′max和柔性短节两端转角θ1、θ2。对于有井壁约束的实际情况，当yc＞0且y′max≥yc+(db-dw)时，管串紧贴下端井壁，此时，管串实际最大挠度为：ymax＝yc+(db-dw)。

以上推导针对的是轴向力pi＜0，即受拉的情况。对于水平井，随着管串的下入，井斜角增大，净重轴向分力减小，此时，由于受到阻力或泵推力的作用，管串可能受到轴向压力，即pi＞0，此时，将ki换成下式并代入以上各式可求得受压时的挠度方程。

s4、根据步骤s1～s3计算出的公式分析出分簇射孔管串在井筒中的变形，根据计算出的变形挠度与转角，可评估该管串在井筒中的通过能力。

当通过性分析模型求解后，在对分簇射孔管串下入过程中遇卡情况、柔性短节安全和井下工具受力情况分析前，现场测试数据如下表和图2～6所示：

一、分簇射孔管串下入过程中遇卡情况，研究结果如图7～9：

实例计算参数中，以1桥塞+4簇射孔枪管串在x206井中下入作业为例，x206井测点从井深3800m开始，井眼内径为114.3mm，研究结果如下：

图7～9所示是管串遇卡时管串挠度与对应井段情况。由图7可知：在前6个测点中，共有3处出现了ymax＜yc的情况，管串在这些位置遇阻，这是因为该井段狗腿度较大、井斜角小；在测点6～32之间为斜井段，狗腿度大且井斜角逐渐增加，故ymax与yc皆较大，此时，有ymax＞yc，管串不会遇阻；在管串下入到测点32之后，ymax与yc变化一致且yc始终小于ymax，这是因为在水平段，管串依靠净重变形而紧贴井壁下端。这些情况与现场实测发现的现象一致。由图8和图9可以看出，电缆泵送分簇射孔管串易在井斜角相对较小、狗腿度相对较大的测点遇卡，这些点主要集中在直井段与斜井段的交界处，这与现场实测情况基本一致。

二、柔性短节安全分析，研究结果如图10：

在管串下入过程中，柔性短节可通过小角度弯曲增强管串通过能力，但其弯曲角度应在许用范围之内。由图10可知：测点30之前为造斜段，柔性短节转角随着井斜角与狗腿度变化而变化；测点30之后为水平段，管串紧贴井筒内壁，短节转角基本不变；柔性短节1与柔性短节2转角皆小于许用转角15°，因此，管串能安全通过井筒。这些与实际情况一致。

三、井下工具受力分析，研究结果如图11和图12：

随着管串的下入，井斜角增大，管串所受阻力越来越大，当阻力大于管串净重轴向分力时，管串停止下入，此时需提供泵推力，推动管串下入到井底。由图11可知：测点1和测点30之间为斜井段，井斜角逐渐增大，故管串轴向分力减小，管串摩擦力增大；测点30以后为水平井段，井斜角在90°左右起伏变化，因此，管串摩擦力变化平稳、轴向力在0n左右波动；井下电缆随着管串的下入逐渐增长，其净重分力在斜井段与水平段产生的摩擦力逐渐增大。由图17可知，计算所得泵推力与实测泵推力在量值上相差较小，在趋势上基本一致。产生一定差异的主要原因是：泵推力的计算十分复杂，不仅与上述各种阻力相关，同时还受到管串结构、泵送液冲击力、流体流速计算方式等因素的影响。