一种基于Pasternak地基模型的层状土中单桩水平振动分析方法与流程

本发明涉及土建领域，更具体地，涉及一种基于pasternak地基模型的层状土中单桩水平振动分析方法。

背景技术：

目前，在解决桩体水平振动动力响应问题时，为方便计算，桩周土体一般简化为winkler模型。winkler地基模型忽略了土的剪切效应，不能反映土体在纵向各层之间的连续性，使得计算结果在理论上不够严密。双参数地基模型在winkler模型的基础上考虑了地基土体剪切效应，更加符合实际。此时采用pasternak地基模型更为合适。

另外，在解决桩体水平振动动力响应问题时，对于细长杆件桩基模型采用经典bernoulli-euler理论，该理论模型只考虑桩体弯曲变形，忽略了桩基剪切变形的影响。而对于大直径桩，考虑桩身剪切变形对其动力阻抗的影响尤为重要，此时桩体采用timoshenko梁模型更为合适。

如何有效地将两者有效结合应用以解决层状土中单桩水平振动分析问题，是本领域研究的重点之一。

技术实现要素：

本发明的目的在于克服现有技术存在的上述缺陷，提供一种基于pasternak地基模型的层状土中单桩水平振动分析方法，采用pasternak地基模型以考虑桩周土体剪切效应，采用分段的timoshenko梁模型模拟桩体以考虑桩体弯曲、剪切变形。

为实现上述目的，本发明的技术方案如下：

一种基于pasternak地基模型的层状土中单桩水平振动分析方法，包括

s1：引入如下假定条件，建立层状土中单桩水平振动分析模型：单桩桩体与桩周土的深度一致，均被纵向分为n层；所述假定条件包括：假定单桩桩体为均质、等截面弹性体，采用timoshenko梁模型；假定桩周土的每层土体均采用pasternak地基模型；假定桩-土耦合振动模型各部分均满足小变形条件，桩土界面为完全接触且无相对滑动；假定桩底为固端约束；

s2：根据timoshenko梁和pasternak地基模型理论建立分层桩身单元的动力平衡方程，所述的动力平衡方程对应的表达式为

同时根据步骤s1中的假定，建立桩-土耦合振动模型边界条件，对应的表达式为：

式中，z为纵向坐标，纵向坐标零点位于自由表面，向下为正，t为时间坐标；n是桩周土和单桩桩体的层数，j是桩周土和单桩桩体自上而下的层数编号，j＝1～n；q0是桩顶水平简谐激振力的振幅，是虚数单位；

a^p、g^p、e^p、i^p、m^p分别为单桩桩体的截面积、剪切模量、弹性模量、截面惯性矩和单位长度质量；k′为单桩桩体的截面的剪力形状系数；b0＝0.9(1.5d+0.5)为单桩桩体的计算宽度，d为单桩桩体的直径，单桩桩体长度为l；

和分别是第j层桩身质点的水平位移和截面转角；和是桩体底部的水平位移和转角，和是桩底顶部的剪力和转角；为第j层桩周土的厚度；为第j层桩周土的刚度系数、阻尼系数和地基剪切系数，各自对应的计算公式为

其中为第j层桩周土的剪切波速，和分别为第j层桩周土的弹性模量、密度、阻尼系数及泊松比，为第j层桩周土的无量纲频率；为第j层桩周土的剪切层厚度；ω是桩顶水平简谐激振力的激振圆频率；

s3：求解步骤s2中所述的分层桩身单元的动力平衡方程以获取层状土中单桩水平振动分析参数，所述参数至少包括水平激振力作用在桩顶的桩顶水平阻抗和桩身任意截面处的内力。

进一步的，所述步骤s3中，求解步骤s2中所述的分层桩身单元的动力平衡方程以获取层状土中单桩水平振动分析参数的过程包括以下步骤

步骤s31：对第j层桩身质点的水平位移、截面转角、桩身剪力以及桩身弯矩分别按照桩顶水平简谐激振力的激振圆频率进行变换，对应的变换公式为：

其中为第j层桩身的水平位移幅值，为第j层桩身的截面转角幅值，为第j层桩身的桩身剪力幅值，为第j层桩身的弯矩幅值；

上述变换公式对应的边界条件变化公式为：

步骤s32：简化分层桩身单元的动力平衡方程以得到水平位移幅值的四阶常微分齐次方程、水平位移幅值通解、转角幅值通解、桩身弯矩幅值通解以及桩身剪力幅值通解，

所述水平位移幅值的四阶常微分齐次方程对应的表达式为：

所述水平位移幅值通解对应的表达式为：

uj(z)＝aj1cosh(βj1z)+aj2sinh(βj1z)+aj3cos(βj2z)+aj4sin(βj2z)；

所述转角幅值通解对应的表达式为：

所述桩身弯矩幅值通解对应的表达式为：

所述桩身剪力幅值通解对应的表达式为：

其中四阶常微分齐次方程中的各符号定义为

w^p＝e^pi^pj^p＝k′a^pg^p

aj1，aj2，aj3，aj4为基于边界条件确定的系数；

其中各通解中的各符号定义为

步骤s33：利用第j层桩身与第j+1层桩身之间的水平位移、转角、弯矩及剪力连续性表达式，建立第j层桩身的系数矩阵方程组；所述第j层桩身的系数矩阵方程组表达式为

求解得到第j层桩身顶部和底部的水平位移、转角、弯矩及剪力的传递关系的表达式为：

bj＝rjaj

其中，是第j层桩身顶部的水平位移幅值、转角幅值、弯矩幅值及剪力幅值构成的状态列向量，是第j+1层桩身顶部的水平位移幅值、转角幅值、弯矩幅值及剪力幅值构成的状态列向量，hj是第j层桩身的厚度；rj是一个4×4的第j层桩身传递矩阵，其分块形式为

各分块阵的表达式为

以上各式中

步骤s34：联立各层桩身的传递矩以得到单桩端部状态列向量与底部状态列向量之间的全长传递关系式，所述全长传递关系式为

bl＝ra0

其中r是单桩的全长传递矩阵，是单桩端部状态列向量，是桩身底部状态列向量，对应的传递矩阵r的分块形式为

其中，所述全长传递关系的分块形式为

步骤s35：给定下述边界条件以得到顶阻抗函数刚度矩阵以及桩顶水平阻抗；所述边界条件为

所述顶阻抗函数刚度矩阵为k＝-r12^-1r11

所述桩顶水平阻抗为

步骤s36：利用桩顶阻抗函数求得桩身任意截面上的内力，对应的计算公式为

其中其中r1至rm-1中的高度hj(j＝1，2，......，m-1)为各土层厚度，rm中的是桩身任意截面的纵向坐标，r^α的分块形式为

从上述技术方案可以看出，本发明基于pasternak地基模型的层状土中单桩水平振动分析方法，能够同时考虑桩周土体剪切效应和桩体弯曲、剪切变形，同时假定桩-土系统各部分均满足小变形条件，桩土界面为完全接触且无相对滑动，桩底为固端约束，最终根据边界条件得到桩顶阻抗函数刚度，以及桩身任意截面上的弯矩和剪力，结果适用于简谐荷载作用下桩基水平振动动力响应问题，可为桩基动力检测提供理论指导和参考作用。

附图说明

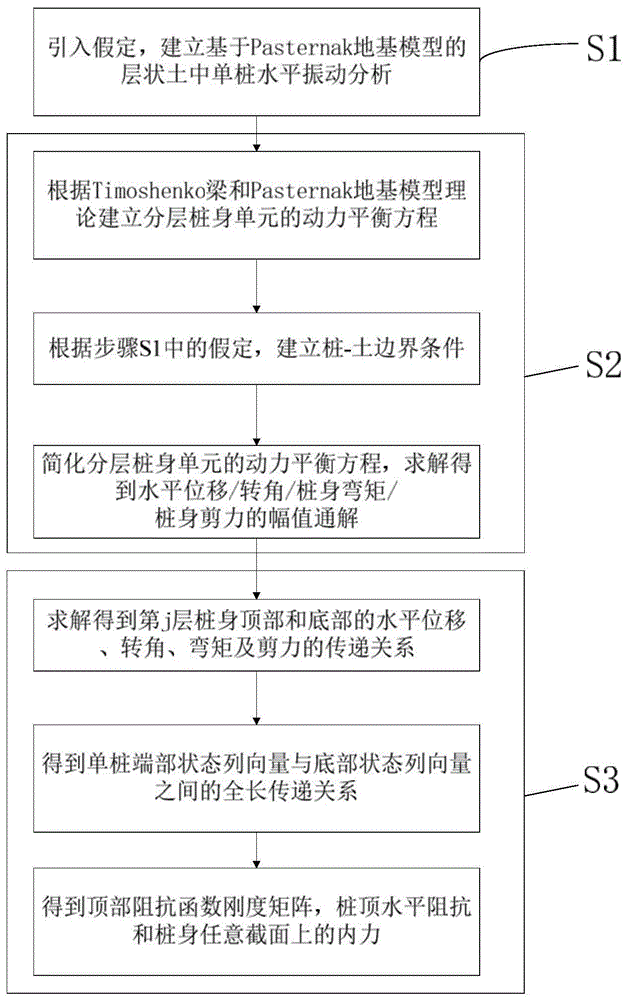
图1为实施例中本发明所述方法对应的核心步骤流程图；

图2为实施例中本发明所述方法对应的模型示意图。

具体实施方式

下面结合附图，对本发明的具体实施方式作进一步的详细说明。

需要说明的是，在下述的具体实施方式中，在详述本发明的实施方式时，为了清楚地表示本发明的结构以便于说明，特对附图中的结构不依照一般比例绘图，并进行了局部放大、变形及简化处理，因此，应避免以此作为对本发明的限定来加以理解。

为解决现有技术所存在的问题，如图1-2所示的一种基于pastemak地基模型的层状土中单桩水平振动分析方法，其特征在于，包括以下步骤：

一种基于pasternak地基模型的层状土中单桩水平振动分析方法，包括

s1：引入如下假定条件，建立层状土中单桩水平振动分析模型：单桩桩体与桩周土的深度一致，均被纵向分为n层；所述假定条件包括：假定单桩桩体为均质、等截面弹性体，采用timoshenko梁模型；假定桩周土的每层土体均采用pasternak地基模型；假定桩-土模型系统各部分均满足小变形条件，桩土界面为完全接触且无相对滑动；假定桩底为固端约束；

s2：根据timoshenko梁和pasternak地基模型理论建立分层桩身单元的动力平衡方程，所述的动力平衡方程对应的表达式为

上述平衡方程相比现有的euler梁模型和winkler地基模型给定了表示桩身剪切模量部分g^p的表达形式同时给定了表示桩周土体剪切系数部分的表达形式；

以通过添加上述内容来构造所需的分层桩身单元的动力平衡方程；

同时根据步骤s1中的假定，建立桩-土模型边界条件，对应的表达式为：

式中，z为纵向坐标，纵向坐标零点位于自由表面，向下为正，t为时间坐标；n是桩周土和单桩桩体的层数，j是桩周土和单桩桩体自上而下的层数编号，j＝1～n；q0是桩顶水平简谐激振力的振幅，是虚数单位；

a^p、g^p、r^p、i^p、m^p分别为单桩桩体的截面积、剪切模量、弹性模量、截面惯性矩和单位长度质量；k′为单桩桩体的截面的剪力形状系数；b0＝0.9(1.5d+0.5)为单桩桩体的计算宽度，d为单桩桩体的直径，单桩桩体长度为l；

和分别是第j层桩身质点的水平位移和截面转角；和是桩体底部的水平位移和转角，和是桩底顶部的剪力和转角；为第j层桩周土的厚度；为第j层桩周土的刚度系数、阻尼系数和地基剪切系数，各自对应的计算公式为

其中为第j层桩周土的剪切波速，和分别为第j层桩周土的弹性模量、密度、阻尼系数及泊松比，为第j层桩周土的无量纲频率：为第j层桩周土的剪切层厚度；ω是桩顶水平简谐激振力的激振圆频率；

s3：求解步骤s2中所述的分层桩身单元的动力平衡方程以获取层状土中单桩水平振动分析参数，所述参数至少包括水平激振力作用在桩顶的桩顶水平阻抗和桩身任意截面处的内力。

进一步的，所述步骤s3中，求解步骤s2中所述的分层桩身单元的动力平衡方程以获取层状土中单桩水平振动分析参数的过程包括以下步骤

步骤s31：对第j层桩身质点的水平位移、截面转角、桩身剪力以及桩身弯矩分别按照桩顶水平简谐激振力的激振圆频率进行变换，对应的变换公式为：

其中为第j层桩身的水平位移幅值，为第j层桩身的截面转角幅值，为第j层桩身的桩身剪力幅值，为第j层桩身的弯矩幅值；

上述变换公式对应的边界条件变化公式为：

步骤s32：简化分层桩身单元的动力平衡方程以得到水平位移幅值的四阶常微分齐次方程、水平位移幅值通解、转角幅值通解、桩身弯矩幅值通解以及桩身剪力幅值通解，

所述水平位移幅值的四阶常微分齐次方程对应的表达式为：

所述水平位移幅值通解对应的表达式为：

uj(z)＝aj1cosh(βj1z)+aj2sinh(βj1z)+aj3cos(βj2z)+aj4sin(βj2z)；

所述转角幅值通解对应的表达式为：

所述桩身弯矩幅值通解对应的表达式为：

所述桩身剪力幅值通解对应的表达式为：

其中四阶常微分齐次方程中的各符号定义为

w^p＝e^pi^pj^p＝k′a^pg^p

aj1，aj2，aj3，aj4为基于边界条件确定的系数；

其中各通解中的各符号定义为

步骤s33：利用第j层桩身与第j+1层桩身之间的水平位移、转角、弯矩及剪力连续性表达式，建立第j层桩身的系数矩阵方程组；所述第j层桩身的系数矩阵方程组表达式为

求解得到第j层桩身顶部和底部的水平位移、转角、弯矩及剪力的传递关系的表达式为：

bj＝rjaj

其中，是第j层桩身顶部的水平位移幅值、转角幅值、弯矩幅值及剪力幅值构成的状态列向量，是第j+1层桩身顶部的水平位移幅值、转角幅值、弯矩幅值及剪力幅值构成的状态列向量，hj是第j层桩身的厚度；rj是一个4×4的第j层桩身传递矩阵，其分块形式为

各分块阵的表达式为

以上各式中

步骤s34：联立各层桩身的传递矩以得到单桩端部状态列向量与底部状态列向量之间的全长传递关系式，所述全长传递关系式为

bl＝ra0

其中r是单桩的全长传递矩阵，是单桩端部状态列向量，是桩身底部状态列向量，对应的传递矩阵r的分块形式为

其中，所述全长传递关系的分块形式为

同时为了表达方便，本部分各个参数暂时去除了下角标0与n，如即为u^p(l)，即为u^p(0)等；

步骤s35：给定下述边界条件以得到顶阻抗函数刚度矩阵以及桩顶水平阻抗；

所述边界条件为

所述顶阻抗函数刚度矩阵为

k＝-r12^-1r11

所述桩顶水平阻抗为

步骤s36：利用桩顶阻抗函数求得桩身任意截面上的内力，对应的计算公式为

其中其中r1至rm-1中的高度hj(j＝1，2，......，m-1)为各土层厚度，rm中的是桩身任意截面的纵向坐标，r^α的分块形式为

以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围之内。