一种彩色图像数字水印实现方法与流程

本发明属于图像处理技术领域，具体涉及一种彩色图像数字水印实现方法。

背景技术：

图像数字水印技术是一种基于内容的、非密码机制的图像信息隐藏技术，是数字媒体版权保护的重要手段。随着成像传感器的发展以及存储成本的降低，彩色图像作为重要的数字媒体信息已被广泛地应用在消费数码、网页、遥感测绘等领域。尤其是在消费数码领域，数字图像和数字视频等各种数字作品在网络上可以很容易的下载并获取。然而，开放的网络环境和便捷的信息处理技术导致了信息安全和图像作品的版权保护问题日趋严重，如何解决诸如图像等数字媒体的版权保护和信息安全已经引起各行业的普遍关注。图像的数字水印技术可以解决该问题，目前已经成为信息安全领域的一个研究热点。

图像数字水印方法是将具有特定含义的水印信息隐藏在图像中，水印信息可以是作品的序列号、公司标志等，用于证明创作者对其作品的所有权，作为鉴定、起诉非法侵权的证据。数字水印方法具有隐蔽性、鲁棒性、确定性等特征。近年来数字水印技术的发展取得了很大进步，一些较为典型的数字水印技术主要有空间域方法、变换域方法、优化类方法等。

空间域方法一般是通过直接修改原始图像的像素值来达到嵌入水印的目的，该方法操作简单但透明性较差。例如经典的最低有效位方法，其原理是通过修改原始数据中的最低有效位来实现水印的嵌入。由于该方法是直接替换了像素最低位，因而鲁棒性较差。

变换域算法一般通过在图像的变换域来修改图像的其它附加属性，如颜色或纹理并嵌入水印。例如经典的基于离散余弦变换的水印方法和基于傅里叶变换的方法等。这种方法可以使图像具有较高鲁棒性的同时保证含有水印的图像具有较好的透明性。但该方法在处理灰度图像时具有较好的效果，但对于彩色图像，添加水印后会存在不同程度的颜色失真问题。

近几年，人工智能及生物模拟算法为图像数字水印技术注入了新活力。例如蚁群算法、粒子群优化算法以及模拟生物遗传的神经网络等。将这些人工智能方法融入图像的数字水印技术中，可以有效的防止图像被串改。但是，此类方法的复杂度较高，并且在处理彩色图像上仍有颜色失真问题。除了上述方法外还有基于分形方法的水印技术、基于奇异值分解的技术等。尽管现有的图像数字水印方法很多，这些方法在处理二值图像以及灰度图像上有着较为成功的应用，但在彩色图像方面，普遍存在颜色失真问题。因此，如何克服彩色图像的数字水印方法的颜色失真问题就显得尤为重要，具有非常重要的研究意义和实用价值。

技术实现要素：

本发明提出了一种彩色图像数字水印实现方法，该方法采用双四元数来表征彩色图像，并且采用双四元数滤波器组在频域嵌入水印信息。该方法能够有效的克服数字水印过程中出现的颜色失真问题。

本发明提出的彩色图像数字水印实现方法的具体实现步骤如下：

步骤s1，将待加密的彩色图像用双四元数进行表示；

步骤s2，使用双四元数分析滤波器组来处理步骤s1中的彩色图像，得到该彩色图像的粗尺度系数矩阵和细尺度系数矩阵；

步骤s3，将数字水印图像进行arnold置乱处理并转换为一维水印序列；

步骤s4，进行水印嵌入位置的选择；

步骤s5，水印信息的嵌入，将步骤s3所得到的一维水印序列嵌入到步骤s4所确定的具体位置中；

步骤s6，使用双四元数综合滤波器组来处理步骤s5中嵌入水印的系数；

步骤s7，从步骤s6所得到的冗余结构的双四元数矩阵恢复出彩色图像，即数字水印嵌入图像的输出。

优选地，所述步骤s1中使用双四元数对彩色图像进行表征的数学公式为：

f＝(fr·i+fg·j+fb·k)+(fr·i+fg·j+fb·k)·i

其中fr、fg和fb分别为彩色图像的r、g和b颜色分量，i、j、k和i分别为双四元数的虚数单位，其运算规则为：

i²＝-1，j²＝-1，k²＝-1，i²＝-1，ij＝-ji＝k，jk＝-kj＝i，ki＝-ik＝j。

优选地，所述步骤s2中双四元数分析滤波器组的滤波系数为：

h0(n)＝(0-0.010.010.080.08-0.690.69-0.08-0.080)·(i+j+k)

h1(n)＝(0-0.080.080.690.690.08-0.080.010.010)·(i+j+k)

g0(n)＝(0-0.08-0.080.69-0.690.080.080.01-0.010)·(i+j+k)

g1(n)＝(00.010.01-0.080.080.690.690.08-0.080)·(i+j+k)

优选地，所述步骤s5中水印信息的嵌入采用冗余排序嵌入方法。

优选地，所述步骤s6中双四元数综合滤波器组的滤波系数是将分析滤波系数进行四元数希尔伯特变换得到的。

与现有技术相比，本发明具有的有益效果是：本发明的算法复杂度低，采用双四元数形式对彩色图像进行冗余表征，通过双四元数分析滤波器组对图像进行子带分解，在频域进行水印嵌入，最后通过综合滤波器组来获取最终的水印图像。本方法在整个处理的过程中始终将彩色图像的三个颜色分量作为一个整体来处理，有效地克服了彩色图像数字水印方法的颜色失真问题，适合于推广使用。

附图说明

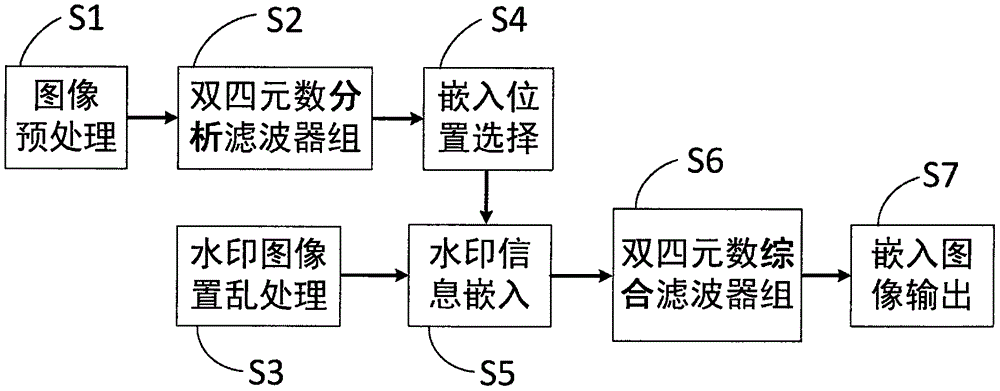
图1为本发明中彩色图像数字水印实现方法流程图；

图2为本发明中双四元数分析滤波器组结构图；

图3为本发明中双四元数综合滤波器组结构图。

具体实施方式

为了便于理解和实施本发明，现结合说明书附图和实施例对本发明的技术方案作进一步详细描述。所描述的实施例仅是本发明一部分实施例，并非全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明提出了一种彩色图像数字水印实现方法，如图1所示，本发明所采取的技术方案如下：

步骤s1，将待加密的彩色图像用双四元数进行表示，使用双四元数对彩色图像进行表征的数学公式为：

f＝(fr·i+fg·j+fb·k)+(fr·i+fg·j+fb·k)·i

其中fr、fg和fb分别为彩色图像的r、g和b颜色分量，i、j、k和i分别为双四元数的虚数单位，其运算规则为：

i²＝-1，j²＝-1，k²＝-1，i²＝-1，ij＝-ji＝k，jk＝-kj＝i，ki＝-ik＝j。

步骤s2，使用双四元数分析滤波器组来处理步骤s1中的彩色图像，得到该彩色图像的粗尺度系数矩阵和细尺度系数矩阵。

图2为本发明中双四元数分析滤波器组结构图，注意该图为一维结构图，若要用其来处理二维图像，是通过先处理行然后再处理列的张量积形式实现的。双四元数分析滤波器组由两组滤波系数构成，分别是h0(n)，h1(n)和g0(n)，g1(n)，这两组滤波系数是对偶的。需要注意的是，上述滤波系数均为长度为n的四元数值数组，在本实施例中，n的取值为10，具体如下：

h0(n)＝(0-0.010.010.080.08-0.690.69-0.08-0.080)·(i+j+k)

h1(n)＝(0-0.080.080.690.690.08-0.080.010.010)·(i+j+k)

g0(n)＝(0-0.08-0.080.69-0.690.080.080.01-0.010)·(i+j+k)

g1(n)＝(00.010.01-0.080.080.690.690.08-0.080)·(i+j+k)

如图2所示，将步骤s1所得到的彩色图像经过双四元数分析滤波器组处理后得到粗尺度系数矩阵ch(3，n)、cg(3，n)以及细尺度系数矩阵dh(1，n)、dg(1，n)、dh(2，n)、dg(2，n)、dh(3，n)和dg(3，n)。需要注意的是，这些粗尺度系数和细尺度系数均为四元数值的矩阵。之所以称图2所示滤波器为“双四元数分析滤波器组”是因为经过该滤波器处理过的彩色图像所得到的粗尺度系数矩阵中的对应元素构成一个双四元数：ch(3，n)作为双四元数的实部，cg(3，n)作为双四元数的虚部。对于细尺度系数矩阵也是如此，这里不再一一赘述。

步骤s3，将数字水印图像进行arnold置乱处理并转换为一维水印序列。在本实施例中，水印图像的大小32×32。arnold置乱处理的本质是对水印图像像素点的位置移动，具体的公式为：

其中，[x′，y′]^t和[x，y]^t分别为原始水印图像和arnold置乱后水印图像的像素位置。

将arnold置乱处理后的水印图像转换为一维水印序列便于后续的图像嵌入处理。需要注意的是，水印图像也要用双四元数进行表征。我们用{wi|i＝0，1，…，1023}来表示arnold置乱处理后的一维水印序列。

步骤s4，进行水印嵌入位置的选择。本方法中选择步骤s2所得到的粗尺度系数矩阵ch(3，n)和cg(3，n)进行水印的嵌入。为了执行冗余排序嵌入方法，需要将粗尺度系数矩阵ch(3，n)转换为一维序列，并按照矩阵元素能量的大小进行降序排列，我们标记该序列为：

{ch(3，n)(i)|i＝0，1，…m-1}，其中m为ch(3，n)的元素个数。

在上述降序排列过程中，需要标记一维序列在原始粗尺度系数矩阵ch(3，n)中的位置，方便由一维序列再还原出二维矩阵形式。

再采用同样的方法将cg(3，n)转换为一维降序排列的序列：

{cg(3，n)(i)|i＝0，1，…m-1}。

步骤s5，水印信息的嵌入，即水印信息的嵌入采用冗余排序嵌入方法。将步骤s3所得到的一维水印序列{wi|i＝0，1，…，1023}的实部按照如下公式嵌入到粗尺度系数矩阵{ch(3，n)(i)|i＝0，1，…m-1}中：

其中，为叠加水印信息后的粗尺度系数，符号“re”表示提取水印元素wi的实部分量。类似地，针对{cg(3，n)(i)|i＝0，1，…m-1}，我们有：

其中，为叠加水印信息后的粗尺度系数，符号“im”表示提取水印元素wi的虚部分量。

在上述两个水印嵌入公式中，α和β代表水印嵌入强度系数，用于协调水印整体的透明度与鲁棒性，在本方法中α和β的取值满足如下约束关系：

α+β＝1

一般情况下，α＝β＝0.5。

根据前面所标记的一维原始粗尺度系数序列在原始粗尺度系数矩阵中的位置对应关系，将叠加水印信息后的一维粗尺度系数还原回二维矩阵形式，便于后续步骤的处理。

步骤s6，使用双四元数综合滤波器组来处理步骤s5中嵌入水印的系数矩阵并得到冗余结构的双四元数矩阵。

图3为本发明中双四元数综合滤波器组结构图，注意该图为一维结构图，若要用其来处理二维图像，也是通过先处理行然后再处理列的张量积形式实现的。双四元数综合滤波器组的滤波系数是将分析滤波系数进行四元数希尔伯特变换得到的，在离散条件下，以为例，可以由h0(n)与1/(πn)进行卷积运算得到：

类似的，我们可以得到和

步骤s7，从步骤s6所得到的冗余结构的双四元数矩阵恢复出彩色图像，具体是取该矩阵的实部分量或虚部分量，最终实现数字水印嵌入图像的输出。

应当说明的是，上述实施例均可根据需要自由组合。以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。