面齿轮同轴分扭传动系统振动特性分析方法及系统与流程

本发明涉及电气工程技术领域，尤其涉及面齿轮同轴分扭传动系统振动特性分析方法及系统。

背景技术：

面齿轮分扭传动主要用于直升机主减速器，取代传统的锥齿轮传动，使得分扭传动结构的重量降低将近40％，同时还有重合度高、配对直齿轮无轴向力、安装简便等优点，面齿轮分扭传动系统设计和制造技术的快速发展极大推动了主减速器和配套直升机的升级换代，为国防工业提供了有效保障。针对面齿轮同轴分扭传动系统空间啮合、闭环功率传递、传动链啮合齿轮副数量多、激励多样和工况复杂等特点，建立对应的数学模型并分析其振动特性和均载特性，研究设计参数与服役性能的关联规律已成为了降低主减速器振动噪声并保证传动系统可靠性而亟待掌握的关键技术。

技术实现要素：

本发明提供了面齿轮同轴分扭传动系统振动特性分析方法及系统，用以解决现有技术中无面齿轮同轴分扭传动系统振动特性分析方法来分析振动特性的技术问题。

为解决上述技术问题，本发明提出的技术方案为：

一种面齿轮同轴分扭传动系统振动特性分析方法，包括以下步骤：

忽略面齿轮同轴分扭传动系统的腹板结构和配对小齿轮的齿轮轴，简化构建面齿轮同轴分扭传动系统的物理模型；

引入啮合刚度、啮合阻尼、静态传动误差激励和齿侧间隙模拟齿轮副啮合效应，以支撑弹簧的刚度模拟轴承的支撑作用，构建面齿轮同轴分扭传动系统的物理模型对应的集中参数法振动分析模型，并推导所述集中参数振动分析模型的运动微分方程；

基于所述集中参数振动分析模型的运动微分方程，得到对应的特征值方程，并通过求解所述特征值方程和运动微分方程，得到系统的固有频率和/或振动模态。

优选的，推导出所述集中参数振动分析模型的运动微分方程，包括以下步骤：

构建所述集中参数振动分析模型中各个齿轮的全局坐标系，并根据所述全局坐标系，确定所述面齿轮同轴分扭传动系统运动所需的广义自由度；

根据所述面齿轮同轴分扭传动系统运动所需的广义自由度，并获取所述面齿轮同轴分扭传动系统中各个齿轮质量、转动惯量、各个齿轮的轴承在x，y和z方向上的支撑刚度、各个齿轮副时变啮合刚度以及面齿轮啮合副沿着啮合线方向的振动位移计算所述面齿轮同轴分扭传动系统的动能和势能；

将面齿轮同轴分扭传动系统的动能和势能带入拉格朗日方程，推导得到矩阵形式的运动方程，并将非线性齿侧间隙函数和比例阻尼引入到所述运动方程中，得到所述集中参数振动分析模型的运动微分方程。

优选的，所述动能为：

式中，t表示系统的动能，i为各个小齿轮的编号，i＝1,2,3,...,np，np为总的小齿轮个数，j为各个面齿轮的编号，j＝1,2,3,...,nf，nf为总的面齿轮个数，mi表示各个小齿轮的质量，ii表示各个小齿轮的转动惯量，xi，yi和zi分别为各个小齿轮在x，y和z方向上的平移自由度，θiz为各个小齿轮绕z轴的转动自由度，mj表示各个面齿轮的质量，ij表示各个面齿轮的转动惯量，xj，yj和zj分别为各个面齿轮在x，y和z方向上的平移自由度，θjz为各个面齿轮绕z轴的转动自由度，符号的上标“.”表示对时间求导数。

优选的，所述势能为弹性支撑势能和弹性啮合势能之和，所述弹性支撑势能为：

式中，kix,kiy,kiz分别为各个小齿轮支撑轴承在x，y和z方向上的支撑刚度，kjx,kjy,kjz分别为各个面齿轮支撑轴承在x，y和z方向上的支撑刚度。

所述弹性啮合势能为：

式中，vm为弹性啮合势能，kij为第i小齿轮与第j个面齿轮构成的啮合副的时变啮合刚度，δij为第i小齿轮和第j个面齿轮构成的啮合副沿着啮合线方向的振动位移。

优选的，所述：

式中，α为齿轮压力角，ri为各个小齿轮的基圆半径，rj为各个面齿轮的啮合力臂，eij(t)为第i小齿轮与第j个面齿轮构成的啮合副的静态传动误差激励，“*”表示局部坐标系。

优选的，所述各个齿轮副时变啮合刚度为：

式中，ωm为啮合频率，tm为啮合周期，t为时间变量，l为阶次，al和bl分别为对应阶次谐波分量的幅值，γij为各个小齿轮和配对面齿轮的啮合相位角，φi为各个小齿轮的分布角，nj为面齿轮的齿数。

优选的，所述运动微分方程为：

其中，m，k，nf和fex分别为系统的质量矩阵、刚度矩阵、非线性啮合力矩阵和外载荷激励，q为系统广义自由度，c为比例阻尼，c＝αm+βk，其中，α和β分别为质量矩阵和刚度矩阵的系数，其中，

式中，cij为各个齿轮啮合副的啮合阻尼，f(δ)为非线性间隙函数，式中，b为齿侧间隙的一半。

优选的，所述特征值方程为：

式中，k为支撑刚度矩阵，km为基于非线性啮合力的啮合刚度矩阵，ωl为系统固有频率，vl为固有频率对应的特征向量，即振动模态，l为广义自由度的数目。

优选的，用龙格库塔数值积分方法求解系统的运动微分方程，得到并分析系统的振动响应和传动性能，其中，所述振动响应和传动性能包括振动位移、动态传动误差和动态均载特性。

一种计算机系统，包括存储器、处理器以及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述任一所述方法的步骤。

本发明具有以下有益效果：

1、本发明中的面齿轮同轴分扭传动系统振动特性分析方法及系统，在考虑空间啮合、闭环齿轮链、工况和激励复杂多样的特性，引入小齿轮分布角、时变啮合刚度、啮合相位差、非线性齿侧间隙和静态传动误差激励等因素，建立系统集中参数法振动特性分析模型，并基于振动特性分析模型，得到固有频率和振动模态等系统特性，为直升机主减速器减振降噪和保证可靠性提供理论基础。

2、在优选的方案中，还可以基于振动特性分析模型，分析得到系统的振动位移、动态传动误差和动态均载特性。

除了上面所描述的目的、特征和优点之外，本发明还有其它的目的、特征和优点。下面将参照附图，对本发明作进一步详细的说明。

附图说明

构成本申请的一部分的附图用来提供对本发明的进一步理解，本发明的示意性实施例及其说明用于解释本发明，并不构成对本发明的不当限定。在附图中：

图1是本发明优选实施例二中的系统简化后物理模型示意图；

图2是本发明优选实施例二中的集中参数法振动分析模型；

图3是本发明优选实施例二中的系统全局坐标系；

图4是本发明优选实施例二中的面齿轮副啮合刚度；

图5是本发明优选实施例二中的面齿轮副啮合刚度谐波分量分布；

图6是本发明优选实施例二中的小齿轮分布角；

图7是本发明优选实施例二中的系统全局坐标系与局部坐标系；

图8是本发明优选实施例二中的系统典型振动模态；

图9是本发明优选实施例二中的上面齿轮振动位移扫频图；

图10是本发明优选实施例二中的尾传惰轮-上面齿轮动态传动误差扫频图；

图11是本发明优选实施例二中的上下面齿轮瞬时均载系数；

图12是本发明优选实施例二中的惰轮瞬时均载系数；

图13是本发明中的面齿轮同轴分扭传动系统振动特性分析方法的流程图。

具体实施方式

以下结合附图对本发明的实施例进行详细说明，但是本发明可以由权利要求限定和覆盖的多种不同方式实施。

实施例一：

如图13所示，本发明公开了一种面齿轮同轴分扭传动系统振动特性分析方法，包括以下步骤：

忽略面齿轮同轴分扭传动系统的腹板结构和配对小齿轮(即直齿轮)的齿轮轴，简化构建面齿轮同轴分扭传动系统的物理模型；

引入啮合刚度、啮合阻尼、静态传动误差激励和齿侧间隙模拟齿轮副啮合效应，以支撑弹簧的刚度模拟轴承的支撑作用，构建面齿轮同轴分扭传动系统的物理模型对应的集中参数法振动分析模型，并推导所述集中参数振动分析模型的运动微分方程；

基于所述集中参数振动分析模型的运动微分方程，得到对应的特征值方程，并通过求解所述特征值方程和运动微分方程，得到系统的固有频率和/或振动模态。

此外，在本实施例中还公开了一种计算机系统，包括存储器、处理器以及存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述计算机程序时实现上述任一所述方法的步骤。

本实施例中的面齿轮同轴分扭传动系统振动特性分析方法及系统，在考虑空间啮合、闭环齿轮链、工况和激励复杂多样的特性，引入小齿轮分布角、时变啮合刚度、啮合相位差、非线性齿侧间隙和静态传动误差激励等因素，建立系统集中参数法振动特性分析模型，并基于振动特性分析模型，得到固有频率和振动模态等系统特性，为直升机主减速器减振降噪和保证可靠性提供理论基础。

实施例二：

实施例二是实施例的优选实施例，其与实施例一的不同之处在于，对所述面齿轮同轴分扭传动系统振动特性分析方法的步骤进行了拓展：

本实施例中提供了一种面齿轮同轴分扭传动系统振动特性的分析方法，考虑空间啮合、闭环齿轮链、工况和激励复杂多样的特性，引入小齿轮分布角、时变啮合刚度、啮合相位差、非线性齿侧间隙和静态传动误差激励等因素，建立系统集中参数法振动特性分析模型，分析研究系统的固有频率、振动模态、振动位移、动态传动误差和动态均载特性，为直升机主减速器减振降噪和保证可靠性提供理论基础。

本发明的目的是这样实现的：

面齿轮同轴分扭传动系统振动特性分析方法，其步骤为：

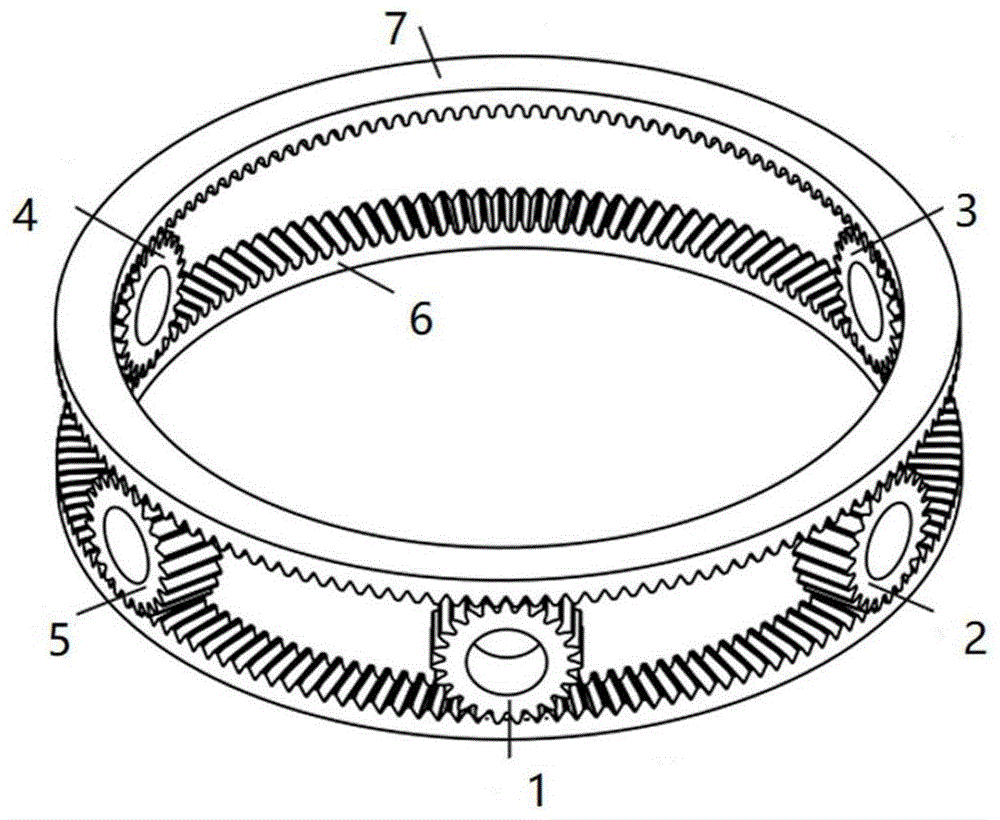
步骤1：设整个面齿轮同轴分扭传动系统包括7个齿轮，其中2个为面齿轮，5个为直齿轮，其中，面齿轮包括上面齿轮7和下面齿轮6，直齿轮包括尾传惰轮1，右惰轮2，右输入轮3，左输入轮4以及左惰轮5，上面齿轮7和下面齿轮6同时与5个直齿轮啮合，总共构成10个齿轮啮合副。输入功率分别由左右两个直齿轮输入，分流到上面齿轮和下面齿轮，下面齿轮传递的功率又通过三个惰轮汇流到上面齿轮最后进行输出。忽略上下面齿轮的腹板结构和配对小齿轮的齿轮轴，得到面齿轮同轴分扭传动系统简化后的物理模型，如图1所示。

步骤2：考虑啮合刚度、啮合阻尼、静态传动误差激励和齿侧间隙等因素模拟齿轮副啮合效应，以支撑弹簧的刚度模拟轴承的支撑作用，得到面齿轮同轴分扭传动系统物理模型对应的集中参数法振动分析模型，如图2所示。

步骤3：推导集中参数法振动分析模型的运动方程。

(3.1)建立7个全局坐标系，并固定到对应的齿轮轮体上，如图3(a)和(b)所示，其中，图3(a)为全局坐标系的正视图，图3(b)为全局坐标系的俯视图。

(3.2)给出描述系统运动所需的广义自由度：

q＝[x1,y1,z1,θ1z,x2,y2,z2,θ2z,...,x7,y7,z7,θ7z]^t(19)

式中，xi，yi和zi分别为各个小齿轮在x，y和z方向上的平移自由度，θiz为各个齿轮绕z轴的转动自由度，i＝1,2,3,4,5表示5个小齿轮，xj，yj和zj分别为各个面齿轮在x，y和z方向上的平移自由度，θjz为各个面齿轮绕z轴的转动自由度，j＝6,7分别表示下面齿轮6和上面齿轮7。

(3.3)给出系统振动的动能：

式中，t表示系统的动能，mi表示各个小齿轮(即直齿轮)的质量，ii表示各个小齿轮的转动惯量，mj表示各个面齿轮的质量，ij表示各个面齿轮的转动惯量，符号的上标“.”表示对时间求导数。

(3.4)给出系统振动的势能：

v＝vs+vm(21)

式中，vs为弹性支撑的势能，vm为弹性啮合势能。

(3.4.1)系统弹性支撑的势能可以写为：

式中，kix,kiy,kiz分别为各个小齿轮支撑轴承在x，y和z方向上的支撑刚度，kjx,kjy,kjz分别为各个面齿轮支撑轴承在x，y和z方向上的支撑刚度。

(3.4.2)基于有限元准静态接触分析，得到面齿轮啮合副的时变啮合刚度曲线和谐波分量分布如图4和图5所示，其中图5上图和下图表示上下面齿轮的啮合刚度的谐波分量。

(3.4.3)基于小齿轮的分布角参数，如图6所示，建立各个小齿轮和配对面齿轮的啮合相位角关系：

式中，φi为各个小齿轮的分布角，n6,n7为下面齿轮6和上面齿轮7的齿数。

(3.4.4)考虑啮合相位差，给出傅里叶级数形式的各个齿轮副时变啮合刚度表达式：

式中，ωm为啮合频率，tm为啮合周期，t为时间变量，l为阶次，al和bl分别为对应阶次谐波分量的幅值。

(3.4.5)基于系统的全局坐标系，建立对应的局部坐标系，如图7所示，其中图7(a)表示下面齿轮的局部坐标系，图7(b)表示上面齿轮的局部坐标系。并推导局部坐标系和全局坐标系的转换关系：

式中，带“*”坐标系为局部坐标系。

(3.4.6)给出10对面齿轮啮合副沿着啮合线方向的振动位移:

式中，α为齿轮压力角，ri为各个小齿轮的基圆半径，r6和r7为下面齿轮6和上面齿轮7的啮合力臂，ei6(t)和ei7(t)为面齿轮啮合副的静态传动误差激励。

(3.4.7)系统弹性啮合势能可以写为:

(3.5)将系统的动能和势能带入拉格朗日方程，推导得到矩阵形式的运动方程：

其中，m，k，nf和fex分别为系统的质量矩阵、刚度矩阵、非线性啮合力矩阵和外载荷激励。q为系统广义自由度。

(3.5.1)将非线性齿侧间隙函数引入非线性啮合力的求解过程，得到新形式的非线性啮合力表达式：

式中，ci6和ci7为各个齿轮啮合副的啮合阻尼。

其中非线性间隙函数可以写为：

式中，b为齿侧间隙的一半。

(3.5.2)将比例阻尼引入到系统运动方程中，得到最终的振动分析模型对应的系统运动微分方程：

其中，比例阻尼矩阵可以写为：

c＝αm+βk(32)

式中，α和β分别为质量矩阵和刚度矩阵的系数。

步骤4：基于面齿轮同轴分扭传动系统的运动微分方程，得到对应的特征值方程，分析系统的固有频率和振动模态。

(4.1)基于运动微分方程推导特征值方程为：

式中，k为支撑刚度矩阵，km为基于非线性啮合力的啮合刚度矩阵，ωl为系统固有频率，vl为固有频率对应的特征向量，即振动模态，l为广义自由度的数目。

(4.2)求解特征值方程，得到系统的固有频率和振动模态，其中典型模态图如图8所示,其中，图8(a)表示在固有频率为1172hz下的模态图，图8(b)表示在固有频率为757hz下的模态图。

步骤5：用龙格库塔数值积分方法求解系统的运动微分方程，得到并分析系统振动位移、动态传动误差和动态均载特性等振动响应和传动性能，结果如图9到图12所示。

综上所述，本发明中的面齿轮同轴分扭传动系统振动特性分析方法及系统，在考虑空间啮合、闭环齿轮链、工况和激励复杂多样的特性，引入小齿轮分布角、时变啮合刚度、啮合相位差、非线性齿侧间隙和静态传动误差激励等因素，建立系统集中参数法振动特性分析模型，并基于振动特性分析模型，得到固有频率和振动模态等系统特性，为直升机主减速器减振降噪和保证可靠性提供理论基础。

以上所述仅为本发明的优选实施例而已，并不用于限制本发明，对于本领域的技术人员来说，本发明可以有各种更改和变化。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。