一种基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法与流程

本发明属于多相催化反应微观动力学分析研究领域，具体涉及一种基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法，可用于复杂催化剂表面反应网络微观动力学方程的高精度、快速、自动化求解。

背景技术：

多相催化在现代化工中有着不可或缺的作用，尤其是在能源转化和环境领域，其中催化剂扮演着关键角色。现如今，高效催化剂的科学设计已成为研究人员的重要目标，但也是挑战难题。相比于传统实验上相对低效的试错法，近二十多年来密度泛函理论(dft)和微观动力学分析的发展，可以促使研究人员从理论上评估催化剂的活性及变化规律，进而有助于催化剂的科学筛选和整体设计。

对于复杂的催化反应体系而言，微观化学基元反应众多，之间互相链接构成了复杂的动力学体系。dft可以从微观层面计算得到每一步基元反应的反应能垒和焓变，以及中间物种的吸附能。基于平均场近似的微观动力学则在微观化学基元反应和宏观催化剂反应活性之间扮演了桥梁作用。通过微观动力学分析，可以得到反应的宏观性质(覆盖度、反应速率等)以及决速因素等，进而来描述催化剂的活性趋势。

基于dft计算数据和微观动力学概念，根据质量作用定律写出基元反应的反应速率表达式，可以推导出化学反应在催化剂表面的速率表达式，然后针对每一个吸附物种，依据物料守恒推导出催化剂表面吸附物种覆盖度随时间变化的一组常微分方程组，最后依据稳态近似(即当反应体系达到稳态时，覆盖度随时间的变化率为0)得到稳态方程组，通过迭代求解可以得到稳态条件下反应的反应速率(催化活性)以及表面中间物种覆盖度等数据，具体流程见图1所示。然而，由于微动力学方程组的复杂性(基元反应多、中间物种多、反应级数不同)和基元反应速率常数之间数量级的差异等引发的刚性问题(stiffproblem)，一般很难快速地得到其精确解。

目前，微观动力学模拟程序chemkin、catmap等采用改进牛顿法进行求解。牛顿法因其收敛速度快而被广泛应用于微观动力学方程组的求解，但需预先给定一个初始值进行迭代求解；当达到给定收敛标准时(可认为体系达到稳态)便终止迭代。求解结果的质量(求解速度、收敛精度和解的合理性)高度依赖于给定的初始值。因此，该方法只有选用合理的初始值，才能快速地得到精确值，否则很难收敛到高精度的解、或者有效解(具有物理意义)；而且由于刚性问题，需要采用高精度数值的计算，才能保证其迭代方向(雅可比矩阵)的有效性和准确性，使得牛顿法迭代通常需要消耗大量的计算机内存和计算时间，特别是在牛顿法求解失败的时候。除此之外，微观动力学模拟程序cantera、mkmcxx等采用高精度数值的时间积分到足够长的时间尺度作为稳态解，高精度数值的时间积分法虽然可以通过迭代达到相对稳定的解，但通常需要很大的时间步长和计算机内存，并且反复迭代，导致求解时间很长；低精度数值的时间积分法虽然更快速，但通常只能得到覆盖度的大概分布趋势，其数量级跟高精度数值结果差别较大，特别是在刚性程度较高的情况下。若简单地结合时间积分和牛顿法交替迭代，虽然有可能实现结合两种方法特点的可能，但采用未达到稳态的覆盖度作为牛顿法的初始值，导致求解结果具有很大的失败概率，同时往返的多次迭代调牛顿法致使需要更长的求解时间，因此，在实际的应用中，该方法依然存在求解时间长、效率低和经常失败等问题。

技术实现要素：

为了克服现有的求解稳态微观动力学方程组求解方法的不足，本发明的目的是提供一种新型的基于时间积分和牛顿法自动联用的方法来实现对稳态动力学方程组的高效求解的方法。其简要思想为：本发明结合了时间积分法可稳定迭代以及牛顿法快速收敛的优点，采用基于低精度数值(16位有效数字)的时间积分法对初始值进行时间积分，结合覆盖度敏感度可快速、自动积分到粗精度的稳态覆盖度，再联用高精度数值(200位有效数字以上)的牛顿法，获得准确、高精度的稳态覆盖度；若单次求解失败，采用指数空间随机初始化覆盖度来进行新一轮的求解，保证搜索空间的广度与多样性，以提高其求解成功率。

为了实现上述目的，本发明采用的技术方案如下：

为了求解稳态动力学方程组，首先通过低精度数值(16位有效数字)的时间积分法对反应初始覆盖度θ0进行时间积分，并快速得到粗精度下的稳态覆盖度θi，使其作为高精度数值(200位有效数字)牛顿法的初始值求解微观动力学稳态方程；当达到收敛标准时(稳态条件)，可得到反应速率以及表面物种覆盖度等宏观性质，进而评价催化剂的反应催化活性或为进一步改进催化剂的催化活性作参考。

本发明的第一方面提供了一种基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法，采用基于低精度数值(16位有效数字)的时间积分法对初始值进行时间积分，结合覆盖度敏感度自动积分到粗精度的稳态覆盖度，再联用高精度数值(200位有效数字以上)的牛顿法，获得稳态覆盖度；若单次求解失败，可在指数空间随机初始化覆盖度来进行新一轮的求解，用于自动化求解催化剂表面化学反应网络的微观动力学方程组，包括以下步骤：

步骤0：输入催化反应体系的微观动力学方程组和反应表面物种(1，…，m)的初始覆盖度行向量θ0＝[θ0,1；…；θ0,m]；

步骤1：利用低精度数值(16位有效数字)的时间积分法，将常微分方程组在时间尺度上从0积分到ti，对应的覆盖度行向量从θ0积分到θi，得到过程中覆盖度随时间的变化，时间变化列向量为t＝[t0,…,ti]，对应的覆盖度变化矩阵为θ＝[θ0,…,θi]；

步骤2：求表面物种m在时间ti的覆盖度敏感度即在对数空间覆盖度随时间的变化斜率，实际求解时采用其差分形式近似根据覆盖度敏感度矩阵x的范数norm(x)是否小于给定的误差(精度)ε，判断其是否趋于稳态；如果是，转到步骤3；否则，更新覆盖度θ0＝θi，提高时间尺度ti＝k×ti，再重复步骤1、2；k表示时间提高系数；

步骤3：利用趋于稳态的粗精度覆盖度θi作为高精度数值(200位有效数字以上)牛顿法的初始值，求解稳态微观动力学方程组高精度的覆盖度θs；

步骤4：判断牛顿法求解是否成功收敛，如果是，转到步骤5；否则，初始化时间尺度ti，随机初始化覆盖度θ0，再重复步骤1、2、3、4。

步骤5：结束。

所述步骤1中常微分方程组由表面各吸附物种覆盖度随时间变化的表达式组成，可由步骤0中微观动力学方程组推导得到。

所述步骤1中覆盖度随时间的变化表示为：dθi/dt＝∑vjrj，其中rj表示基元反应j的反应速率，vj表示反应速率rj前面的系数；对应的时间积分形式表示为：

所述步骤1中的初始时间尺度ti的最优值在10^-15到10^-8之间。

所述步骤1中的时间积分法采用低精度数值(16位有效数字)的刚性常微分方程组求解，具体如matlab刚性常微分方程组求解器ode15s、ode23s、ode23t、ode23tb等中的一种。

所述步骤2中的覆盖度敏感度这一概念由本发明提出；式中，t表示时间，θ表示覆盖度。

所述步骤2中的log()为取对数函数，其底数可以是以任何正数，其中优选的底数为10。

所述步骤2中的覆盖度敏感度矩阵x＝[x1,…,xi]为覆盖度矩阵与时间向量在对数空间的差分，其中在任一时间tk各个表面物种覆盖度的敏感度行向量为xk＝[xk,1；…；xk,m]，对于表面物种m其具体形式为：k∈[1,i]。

所述步骤2中的范数为度量欧氏距离表示矩阵元素的平方和再开平方；式中，n表示任一表面物种，m表示表面物种的个数，k表示任一时间，i表示时间ti，x表示覆盖度敏感度矩阵。(说明：先把某一物种n从0到ti时间上(对应下标k)覆盖度敏感度的平方xk,n²全部加起来，再把所有的物种加起来。)

所述步骤2中的误差(精度)ε的最优值在10^-8到10^-4之间。

所述步骤2中的时间提高系数k的最优值在10¹到10³之间。

所述步骤3中的牛顿法为受约束的改进牛顿迭代法(dampednewtonmethod)，所受的约束为：所有覆盖度的取值在0到1之间。

所述步骤3中的牛顿法求解需要采用高精度数值，并且精度最优值在200位有效数值以上。

所述步骤4中的随机初始化覆盖度采用指数空间随机数，即各覆盖度之间有数量级的差别。

所述步骤4中的牛顿法求解若失败，将采用随机初始化覆盖度来进行新一轮的求解，保证了搜索空间的广度与多样性。

由于采用上述技术方案，本发明具有以下优点和有益效果：

本发明的基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法中，低精度数值的时间积分法被用来对初始值进行积分，使其稳态下的粗精度初始值包含在高精度数值的牛顿法的收敛域中。一旦牛顿法迭代开始收敛，它就会迅速收敛到稳定的解。数值解从粗到细、从低到高的过程进一步增强了牛顿法的收敛性和求解速度。

本发明的基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法具有如下优点：相比于单独使用时间积分法、牛顿法求解或简单结合时间积分/牛顿法交替迭代法，本发明的方法对求解稳态微观动力学方程组具有更高的成功率、速度和精度；同时本发明自动化程度高，只需要设定初始参数，就可以实现自动化迭代求解，过程不需要人机互动，而且算法流程简单，容易上手。

本发明的基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法利用输入的随机初始覆盖度，便可自动求解，并得到稳态条件下高精度的覆盖度和反应速率等宏观性质。其步骤为，采用基于低精度数值(16位有效数字)的时间积分法对初始值进行时间积分，结合覆盖度敏感度可快速、自动积分到粗精度的稳态覆盖度，再联用高精度数值(200位有效数字以上)的牛顿法，获得准确、高精度的稳态覆盖度；若单次求解失败，可在指数空间随机初始化覆盖度来进行新一轮的求解，提高搜索空间的广度与多样性，保证求解成功率，可用于快速、自动化求解催化剂表面化学反应网络的微观动力学方程组。本发明可自动化实现微观动力学方程组的求解，兼具更高的求解成功率和速度，适用于复杂的多相催化反应体系，具有显著的应用前景。

附图说明

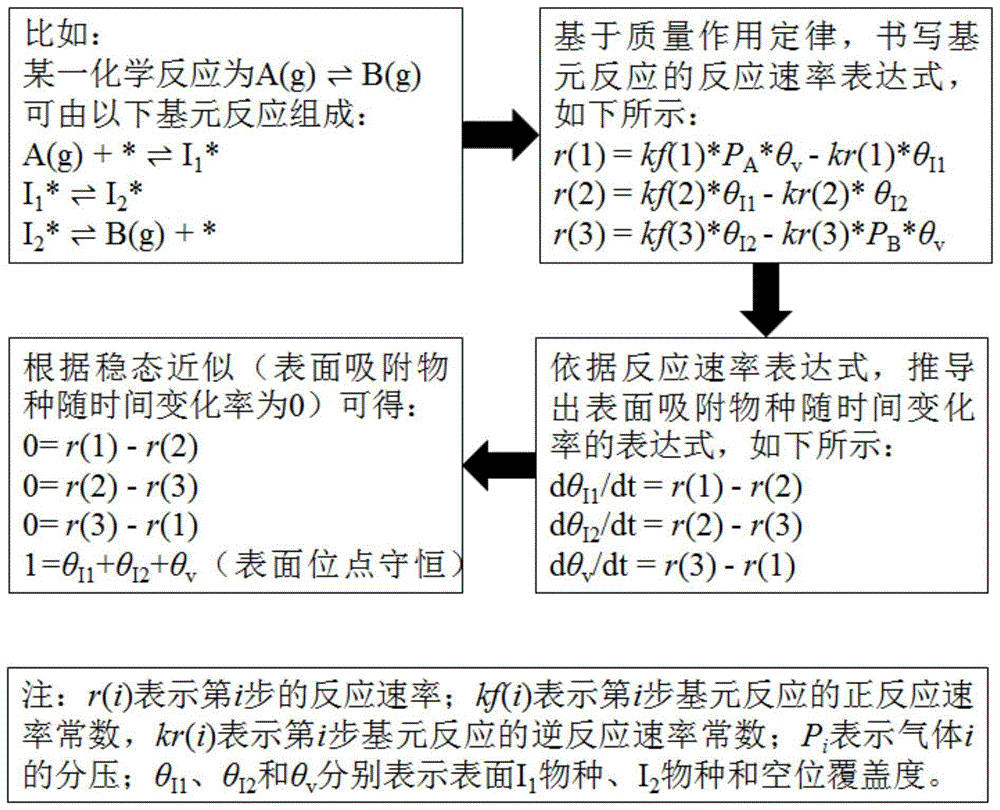
图1是现有技术中依据化学基元反应书写反应速率表达式、常微分方程组和稳态微观动力学方程组的流程示意图。

图2是本发明的基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的流程示意图。

图3是实施例1的结果示意图，其中，(a)为牛顿法的求解结果；(b)为本发明的求解结果；其中黑色方块表示使用时间积分法进行迭代结果，黑色圆形表示牛顿法迭代结果；纵坐标为收敛残差精度，横坐标为迭代步数。

图4是实施例1的结果示意图，其中，(a)为牛顿法的求解结果；(b)为本发明的求解结果；其中黑色全填充指设置初始值为普通随机数测试结果，黑色条纹填充指设置初始值为指数空间随机数测试结果；纵坐标为求解成功率，横坐标对应求解方法。

图5是实施例2的结果示意图，其中，(a)为牛顿法的求解结果，其中黑色全填充表示牛顿法求解失败，黑色条纹填充表示牛顿法求解成功；(b)为本发明的求解结果，其中黑色全填充表示时间积分求解，黑色条纹填充表示牛顿法求解；纵坐标表示求解时长，横坐标对应求解方法。

图6是实施例3的结果示意图，其中，虚线为牛顿法的求解结果；实线为本发明的求解结果；纵坐标表示求解成功率，横坐标对应中间体i的吸附能。

具体实施方式

为了更清楚地说明本发明，下面结合优选实施例对本发明做进一步的说明。本领域技术人员应当理解，下面所具体描述的内容是说明性的而非限制性的，不应以此限制本发明的保护范围。

为了求解稳态动力学方程组，首先通过低精度数值(16位有效数字)的时间积分法对反应初始覆盖度θ0进行时间积分，并快速得到粗精度下的稳态覆盖度θi，使其作为高精度数值(200位有效数字)牛顿法的初始值求解微观动力学稳态方程；当达到收敛标准时(稳态条件)，可得到反应速率以及表面物种覆盖度等宏观性质，进而评价催化剂的反应催化活性或为进一步改进催化剂的催化活性作参考。

本发明实施例的一方面提供了一种基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法(如图1所示)，采用基于低精度数值(16位有效数字)的时间积分法对初始值进行时间积分，结合覆盖度敏感度自动积分到粗精度的稳态覆盖度，再联用高精度数值(200位有效数字以上)的牛顿法，获得稳态覆盖度；若单次求解失败，可在指数空间随机初始化覆盖度来进行新一轮的求解，用于自动化求解催化剂表面化学反应网络的微观动力学方程组，包括以下步骤：

步骤0：输入催化反应体系的微观动力学方程组和反应表面物种(1，…，m)的初始覆盖度行向量θ0＝[θ0,1；…；θ0,m]；

步骤1：利用低精度数值(16位有效数字)的时间积分法，将常微分方程组在时间尺度上从0积分到ti，对应的覆盖度行向量从θ0积分到θi，得到过程中覆盖度随时间的变化，时间变化列向量为t＝[t0,…,ti]，对应的覆盖度变化矩阵为θ＝[θ0,…,θi]；

步骤2：求表面物种m在时间ti的覆盖度敏感度即在对数空间覆盖度随时间的变化斜率，实际求解时采用其差分形式近似根据覆盖度敏感度矩阵x的范数norm(x)是否小于给定的误差(精度)ε，判断其是否趋于稳态；如果是，转到步骤3；否则，更新覆盖度θ0＝θi，提高时间尺度ti＝k×ti，再重复步骤1、2；k表示时间提高系数；

步骤3：利用趋于稳态的粗精度覆盖度θi作为高精度数值(200位有效数字以上)牛顿法的初始值，求解稳态微观动力学方程组高精度的覆盖度θs；

步骤4：判断牛顿法求解是否成功收敛，如果是，转到步骤5；否则，初始化时间尺度ti，随机初始化覆盖度θ0，再重复步骤1、2、3、4。

步骤5：结束。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤1中常微分方程组由表面各吸附物种覆盖度随时间变化的表达式组成，可由步骤0中微观动力学方程组推导得到。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤1中覆盖度随时间的变化表示为：dθi/dt＝∑vjrj，其中rj表示基元反应j的反应速率，vj表示反应速率rj前面的系数；对应的时间积分形式表示为：

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤1中的初始时间尺度ti的最优值在10^-15到10^-8之间。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤1中的时间积分法采用低精度数值(16位有效数字)的刚性常微分方程组求解，具体如matlab刚性常微分方程组求解器ode15s、ode23s、ode23t、ode23tb等中的一种。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤2中的覆盖度敏感度这一概念由本发明提出；式中，t表示时间，θ表示覆盖度。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤2中的log()为取对数函数，其底数可以是以任何正数，其中优选的底数为10。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤2中的覆盖度敏感度矩阵x＝[x1,…,xi]为覆盖度矩阵与时间向量在对数空间的差分，其中在任一时间tk各个表面物种覆盖度的敏感度行向量为xk＝[xk,1；…；xk,m]，对于表面物种m其具体形式为：k∈[1,i]。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤2中的范数为度量欧氏距离表示矩阵元素的平方和再开平方；式中，n表示任一表面物种，m表示表面物种的个数，k对应任一时间，i对应时间ti，x表示覆盖度敏感度矩阵。即norm(x)表示先把某一物种n从0到ti时间上(对应下标k从1到i)的覆盖度敏感度的平方xk,n²全部加起来，再从1到m累加所有的物种n，最后开平方。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤2中的误差(精度)ε的最优值在10^-8到10^-4之间。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤2中的时间提高系数k的最优值在10¹到10³之间。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤3中的牛顿法为受约束的改进牛顿迭代法(dampednewtonmethod)，所受的约束为：所有覆盖度的取值在0到1之间。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤3中的牛顿法求解需要采用高精度数值，并且精度最优值在200位有效数值以上。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤4中的随机初始化覆盖度采用指数空间随机数，即各覆盖度之间有数量级的差别。

根据本发明所述基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的一个实施方式，所述步骤4中的牛顿法求解若失败，将采用随机初始化覆盖度来进行新一轮的求解，保证了搜索空间的广度与多样性。

实施例1

pt(111)表面催化co氧化反应生成co2过程的微动力学分析。

如图2所示，图2是本发明的基于时间积分和牛顿法自动联用高效求解稳态微观动力学方程组的方法的流程示意图。

反应条件：co、o2和co2的分压分别为0.01、0.2和0.002atm，反应温度为300k，反应机理、反应自由能垒和反应自由能如表1所示：

表1

其中能量数据均由量子化学软件vasp计算得到。

首先，依据质量作用定律，每个基元反应的反应速率表达式可写为：

r(1)＝kf(1)*pco*θv-kr(1)*θco

r(2)＝kf(2)*po2*θv²-kr(2)*θo²

r(3)＝kf(3)*θco*θo-kr(3)*pco²*θv²

其中，r(i)表示第i步的反应速率；kf(i)表示第i步基元反应的正反应速率常数，kr(i)表示第i步基元反应的逆反应速率常数；pi表示气体i的分压；θco、θo和θv分别表示表面co物种、o物种和空位覆盖度，θo²、θv²分别表示θo、θv对应的平方项。

针对每一个表面吸附物种，基于以上反应速率表达式，可推导出表面各吸附物种覆盖度随时间变化的表达式，如以下常微分方程组所示：

dθco/dt＝r(1)-r(3)

dθo/dt＝2*r(2)-r(3)

dθv/dt＝2*r(3)-2*r(2)-r(1)

然后依据稳态近似(即物种覆盖度随时间的变化率为0)，可得到稳态非线性方程组，如下所示：

r(1)-r(3)＝0

2*r(2)-r(3)＝0

θv+θo+θco＝1(表面位点守恒)

实现该方法的迭代参数设置：步骤0中初始值覆盖度设置为θ0＝[θco；θo；θv]＝[0；0；1]；步骤1中初始时间尺度ti为10^-10，时间积分法采用matlab刚性常微分方程组求解器ode15s；步骤2中误差(精度)ε为10^-6，时间提高系数k为10²；步骤3中牛顿法求解采用300位高精度数值计算(收敛精度10^-300)。

为了证明该方法的求解效率，分别使用单独牛顿法和时间积分+牛顿法自动联用法即本申请所使用的方法对该实施例求解，得到的收敛残差随迭代步演化曲线如图3所示；图3是实施例1的结果示意图，其中，(a)为牛顿法的求解结果；(b)为本发明的求解结果；其中黑色方块表示使用时间积分法进行迭代结果，黑色圆形表示牛顿法迭代结果；纵坐标为收敛残差精度，横坐标为迭代步数。同时进一步做了1000组在随机初始值下(初始值覆盖度θ0)的求解测试，包括普通随机数(各覆盖度处于同一数量级)和指数空间随机数(各覆盖度之间有数量级的差别)，得到求解成功率如图4所示，图4是实施例1的结果示意图，其中，(a)为牛顿法的求解结果；(b)为本发明的求解结果；其中黑色全填充指设置初始值为普通随机数测试结果，黑色条纹填充指设置初始值为指数空间随机数测试结果；纵坐标为求解成功率，横坐标对应求解方法。

从图3中可以看出，图3中两种方法选用初始值覆盖度设置均为θ0＝[θco；θo；θv]＝[0；0；1]；从求解结果可看出，牛顿法迭代前40步残差很快收敛到10^-10以下，但最终迭代到1000步也没达到收敛精度(10^-300)，并且此时对应的表面覆盖度与稳态覆盖度截然不同，说明初始值覆盖度设置不合理。而采用时间积分+牛顿法自动联用法即本申请所使用的方法求解，时间积分法迭代9步，覆盖度则趋于稳态；以此作为牛顿法初始值进行迭代求解，迭代7步就可达到收敛精度(10^-300)。因此，对比可看出，本发明能更高效地得到求解结果。

依据1000组测试结果，从图4可看出，相比于牛顿法，不管初始值覆盖度设置是普通随机数还是指数空间随机数，时间积分+牛顿法自动联用法即本申请所使用的方法求解成功率均达到100％。因此，本发明方法对初始值的选择具有广泛性，并具有更高的求解成功率。

实施例2

fe(211)表面催化n2和h2反应生成nh3(合成氨反应)的微动力学分析。

反应条件：反应温度为723k，反应压力：h2、n2、nh3分别为75、25、11.6atm；反应机理、反应自由能垒和反应自由能如表2所示：

表2

其中能量数据均由量子化学软件vasp计算得到。

首先，依据质量作用定律，每个基元反应的反应速率表达式可写为：

r(1)＝kf(1)*pn2*θv²-kr(1)*θn²

r(2)＝kf(2)*ph2*θv²-kr(2)*θh²

r(3)＝kf(3)*θh*θn-kr(3)*θnh*θv

r(4)＝kf(4)*θh*θnh-kr(4)*θnh2*θv

r(5)＝kf(5)*θh*θnh2-kr(5)*θnh3*θv

r(6)＝kf(6)*θnh3-kr(6)*pnh3*θv

其中，r(i)表示第i步的反应速率；kf(i)表示第i步基元反应的正反应速率常数，kr(i)表示第i步基元反应的逆反应速率常数；pi表示气体i的分压；θn、θh、θnh、θnh2、θnh3和θv分别表示表面n物种、h物种、nh物种、nh2物种、nh3物种和空位覆盖度。θv²、θn²、θh²分别表示θv、θn、θh对应的平方项。

针对每一个表面吸附物种，基于以上反应速率表达式，可推导出表面各吸附物种覆盖度随时间变化的表达式，如以下常微分方程组所示：

dθh/dt＝2*r(2)-r(3)-r(4)-r(5)

dθn/dt＝2*r(1)-r(3)

dθnh/dt＝r(3)-r(4)

dθnh2/dt＝r(4)-r(5)

dθnh3/dt＝r(5)-r(6)

dθv/dt＝r(3)-2*r(2)-2*r(1)+r(4)+r(5)+r(6)

然后依据稳态近似(即物种覆盖度随时间的变化率为0)，可得到稳态非线性方程组，如下所示：

2*r(2)-r(3)-r(4)-r(5)＝0

2*r(1)-r(3)＝0

r(3)-r(4)＝0

r(4)-r(5)＝0

r(5)-r(6)＝0

θh+θn+θnh+θnh2+θnh3+θv＝1(表面位点守恒)

实现该方法的迭代参数设置：步骤0中初始值覆盖度设置为θ0＝[θh；θn；θnh；θnh2；θnh3；θv]＝[0；0；0；0；0；1]；步骤1中初始时间尺度ti为10^-10，时间积分法采用matlab刚性常微分方程组求解器ode15s；步骤2中误差(精度)ε为10^-6，时间提高系数k为10²；步骤3中牛顿法求解采用300位高精度数值计算(收敛精度10^-300)。

为了证明该方法的求解效率，分别使用单独牛顿法和时间积分+牛顿法自动联用法即本申请所使用的方法对该实施例进行了100组求解测试，其中初始值设置采用指数空间随机数模式。得到求解成功概率如图5所示，图5是实施例2的结果示意图，其中，(a)为牛顿法的求解结果，其中黑色全填充表示牛顿法求解失败，黑色条纹填充表示牛顿法求解成功；(b)为本发明的求解结果，其中黑色全填充表示时间积分法求解，黑色条纹填充表示牛顿法求解；纵坐标表示求解时长，横坐标对应求解方法。

从图5可以看出，单独牛顿法单次求解平均需要约550s，其中主要求解失败的原因是需要较长的迭代时间650s(550/85％)，但成功求解也需0.84s(0.13s/15％)；相比于单独牛顿法求解，采用时间积分+牛顿法自动联用法即本申请所使用的方法求解的成功率可达100％，并且单次平均求解时间仅需约2.56s，比单独牛顿法快了2个数量级以上，其中消耗时间(2.46s)的方法主要为时间积分法，而后续的牛顿法求解仅仅只需0.10s。因为通过时间积分法到稳态提供了更好的初始值，再用牛顿法求解将具有更高的成功求解概率和更少的求解时间。而对于简单地结合时间积分/牛顿法交替迭代法，因为采用未达到稳态的覆盖度作为牛顿法的初始值，所以会有很大的求解失败概率，同时由于需要多次迭代调牛顿法而更加的耗时。综上所述，本发明的方法具有更高的成功求解率和求解速度。

实施例3

金红石110表面上催化碘还原反应的微动力学分析。

反应条件：反应温度为298.15k，反应浓度：i2、i^-和e分别为0.03、0.6和1mol/l；反应机理、反应自由能垒和反应自由能与i的吸附能eadsⁱ的线性关系如表3所示：

表3

其中能量数据均由量子化学软件vasp计算得到。

首先，依据质量作用定律，每个基元反应的反应速率表达式可写为：

r(1)＝kf(1)*ci2*θv²-kr(1)*θi²

r(2)＝kf(2)*ce*θi-kr(2)*ci^-*θv

其中，r(i)表示第i步的反应速率；kf(i)表示第i步基元反应的正反应速率常数，kr(i)表示第i步基元反应的逆反应速率常数；ci表示物种i的浓度；θi和θv分别表示表面i物种和空位覆盖度，θi²、θv²分别表示θi、θv对应的平方项。

针对每一个表面吸附物种，基于以上反应速率表达式，可推导出表面各吸附物种覆盖度随时间变化的表达式，如以下常微分方程组所示：

dθi/dt＝2*r(1)-r(2)

dθv/dt＝r(2)–2*r(1)

然后依据稳态近似(即物种覆盖度随时间的变化率为0)，可得到稳态非线性方程组，如下所示：

2*r(1)-r(2)＝0

θv+θi＝1(表面位点守恒)

实现该方法的迭代参数设置：步骤0中初始值覆盖度设置为θ0＝[θi；θv]＝[0；1]；步骤1中初始时间尺度ti为10^-10，时间积分法采用matlab刚性常微分方程组求解器ode15s；步骤2中误差(精度)ε为10^-6，时间提高系数k为10²；步骤3中牛顿法求解采用300位高精度数值计算(收敛精度10^-300)。

为了证明该方法的求解效率和稳定性，分别使用单独牛顿法和时间积分+牛顿法自动联用法即本申请所使用的方法对该实施例求解，在每个i吸附能上都进行了100组的求解测试，其中初始值设置采用指数空间随机数模式，得到求解成功率随i吸附能(eadsⁱ)的曲线如图6所示；图6是实施例3的结果示意图，其中，虚线为牛顿法的求解结果；实线为本发明的求解结果。从图6可以看出，在不同i吸附能上，单独牛顿法求解的成功率基本不高，而且变化很大(不稳定)，采用时间积分+牛顿法自动联用法即本申请所使用的方法求解的成功率在整个i吸附能上都可达100％。因此，本发明的方法具有更高的成功求解率和求解稳定性。

以上所述仅是本发明的较佳实施例而已，并非对本发明作任何形式上的限制，虽然本发明已以较佳实施例揭露如上，然而并非用以限定本发明，任何熟悉本专利的技术人员在不脱离本发明技术方案范围内，当可利用上述提示的技术内容作出些许更动或修饰为等同变化的等效实施例，但凡是未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与修饰，均仍属于本发明方案的范围内。