一种基于SSA-SVR模型的高炉铁水硅含量预测方法与流程

本发明涉及高炉铁水硅含量预测技术领域，尤其涉及一种基于ssa-svr模型的高炉铁水硅含量预测方法。

背景技术：

在高炉炼铁过程中，铁水中的硅含量是高炉优化控制的关键参数。因此，建立一个合理准确预测硅含量的模型可以为高炉操作者提前判断炉况变化趋势以及调控幅度提供参考依据，进而保证炼铁过程顺利进行，使得铁水质量保持在正常范围内，从而遏制可能发生的故障并降低能耗。

由于高炉冶炼数据具有强烈的非线性特征，基于支持向量机(svm)的硅含量预测模型研究成为了当前的主流方法之一，现有技术中有采用最小二乘法支持向量机模型，有将小波理论与支持向量机结合建立预测模型，但支持向量机预测的效果在很大程度上依赖于良好的训练集。然而，由于机理复杂、环境恶劣、高温高压等因素的影响，高炉冶炼过程中采集的数据中含有大量噪声，因此，必须采取合理的方法降低数据噪声才能获得准确的预测模型。

技术实现要素：

(一)要解决的技术问题

基于上述问题，本发明提供一种基于ssa-svr模型的高炉铁水硅含量预测方法，采用奇异谱分析/ssa方法降低数据噪声，使得支持向量机回归/svr的硅含量预测模型的预测更准确。

(二)技术方案

基于上述的技术问题，本发明提供一种基于ssa-svr模型的高炉铁水硅含量预测方法，所述方法包括以下步骤：

s1、对原始数据进行预处理：选取决策属性数据即硅含量数据，及与硅含量相关的条件属性数据，补全缺失值，对数据进行归一化处理，获得模型所需要的训练数据集和测试数据集；

s2、经奇异谱分析/ssa方法进行数据降噪：将所述训练数据集的一种条件属性数据分解为独立的具有解释性的分量，包括趋势分量、波动分量和噪声分量，然后基于改进的奇异谱分析判决方法去除噪声分量，将趋势分量和波动分量重构为去噪数据集，再对所述训练数据集中的其它条件属性数据重复步骤s2；

s3、svr建模与优化：建立svr预测模型，并利用十字交叉算法对svr参数寻优，将得到的最佳参数传递给所述svr预测模型；

s4、硅含量预测：利用所述训练数据集训练得到的所述svr预测模型对高炉铁水中的硅含量进行预测。

进一步的，步骤s1所述的与硅含量相关的条件属性数据采用粗糙集进行约简，所述的与硅含量相关的条件属性数据包括：富氧率，透气性指数，标准风速，鼓风动能，炉富煤气量，炉富煤气量指数，理论燃烧温度，冷风压力，热风压力，实际风速，以及热风温度。

进一步的，步骤s2包括以下步骤：

s2.1、分解分量：将所述训练数据集的一种条件属性数据分解为独立的具有解释性的分量，包括趋势分量、波动分量和噪声分量；包括以下步骤：

s2.1.1、构造轨迹矩阵，所述轨迹矩阵为：

其中k＝n-l+1，l为窗口长度，2≤l≤n，n为训练数据集的数据总个数，yk为一种条件属性数据的训练数据集的原始数据，k＝1,2,…,n；

s2.1.2、奇异值分解：采用协方差矩阵s＝xx^t，然后利用s的奇异值分解方法生成l个奇异值，即特征值λ1，λ2，...，λl，以及对应的特征向量u1，u2，...，ul，从l个奇异值中选出d个不为0的奇异值，则所述轨迹矩阵重写为：

x＝x1+x2+...+xd，0<d≤l，

其中，i＝1,2,…,d，λi、ui分别为奇异值及其对应的特征向量，向量vi为主成分向量；

s2.2、分量重构：基于改进的奇异谱分析判决方法去除噪声分量，将趋势分量和波动分量重构为去噪数据集；包括以下步骤：

s2.2.1、分组：第一个奇异值代表原始数据的变化趋势，即为趋势分量，再基于改进的奇异谱分析判决方法去除噪声分量，得到波动分量；

s2.2.2、重构：通过对角平均，通过如下公式将每一个xi转为一个时间序列，该时间序列是初始时间序列的一个和分量，即

其中，yk^*为该时间序列的子项，表示一种条件属性数据的训练数据集的重构数据，k＝1,2,…,n，zpq表示一个(l×k)的对角平均转移矩阵z的每一个元素，1≤p≤l，1≤q≤k，

l^*＝min(l,k),k^*＝max(l,k),n＝k+l-1。

进一步的，所述步骤s2.2.1中所述的改进的奇异谱分析判决方法包括：

s2.2.1.1、构建奇异值曲线图：横轴为第i个奇异值，纵轴为奇异值λi；

s2.2.1.2、对不包含第一个奇异值部分的奇异值曲线进行微分，获得奇异值斜率变化曲线f(λi)；

s2.2.1.3、设置阈值a，若f(λi)>a，则表明第i个奇异值属于波动分量，否则属于噪声分量。

进一步的，所述步骤s3包括以下步骤：

s3.1、基于支持向量机回归建立svr预测模型：将步骤s1中所述的条件属性数据作为所述svr预测模型的输入向量，将步骤s1中所述的决策属性数据作为所述svr预测模型的输出向量；

s3.2、对所述svr模型执行十字交叉算法，求解svr预测模型的最佳参数；

s3.3、将上述求得的最佳参数传递给svr预测模型，训练样本数据建立最佳svr预测模型。

进一步的，所述步骤s3.1包括以下步骤：

s3.1.1、设置所述svr预测模型的输入量为条件属性数据xt，设置所述svr预测模型的输出向量为对应条件属性数据xt的决策属性数据yt，其中t＝1,2,3…,n；

s3.1.2、将所述的条件属性数据xt和所述的决策属性数据yt构成数据集(xt,yt)并采用非线性映射核函数将数据映射到高维空间，构成所述svr预测模型函数；

s3.1.3、引入非负的松弛变量和拉格朗日函数，利用库恩塔克条件，将svr预测模型函数f(x)写为

其中，αt，αt^*是拉格朗日乘子，k(xt,x)是核函数，b为svr预测模型阈值；

s3.1.4、确定所述核函数，建立所述svr预测模型。

进一步的，步骤s3.1.4所述的核函数为高斯核函数，则所述svr预测模型为：

其中，σ为高斯核函数的带宽。

(三)有益效果

本发明的上述技术方案具有如下优点：

(1)本发明解决了异常数据和含有噪声数据导致的建模不可靠的问题，将奇异谱分析ssa方法引入高炉冶炼数据处理，将数据分解为趋势分量、波动分量以及噪声分量，在保留有效数据分量的前提下，去除噪声分量，大大降低了建立不可靠模型的风险，能有效防止预测模型出现过拟合、甚至不稳定的现象，提高预测模型的准确度；

(2)本发明提出了一种改进的奇异谱分析判决方法，该方法对奇异值曲线进行微分，建立奇异值斜率变化曲线图，并定义阈值，实现噪声分量与波动分量分割的稳定性，有效区分波动分量和噪声分量，提高了降噪的有效性，避免传统人为选择的随意性与不确定性，从而提高预测模型的精确性；

(3)本发明基于支持向量机回归建立svr模型能够很好地作用于非线性系统，具有良好的泛化能力。

附图说明

通过参考附图会更加清楚的理解本发明的特征和优点，附图是示意性的而不应理解为对本发明进行任何限制，在附图中：

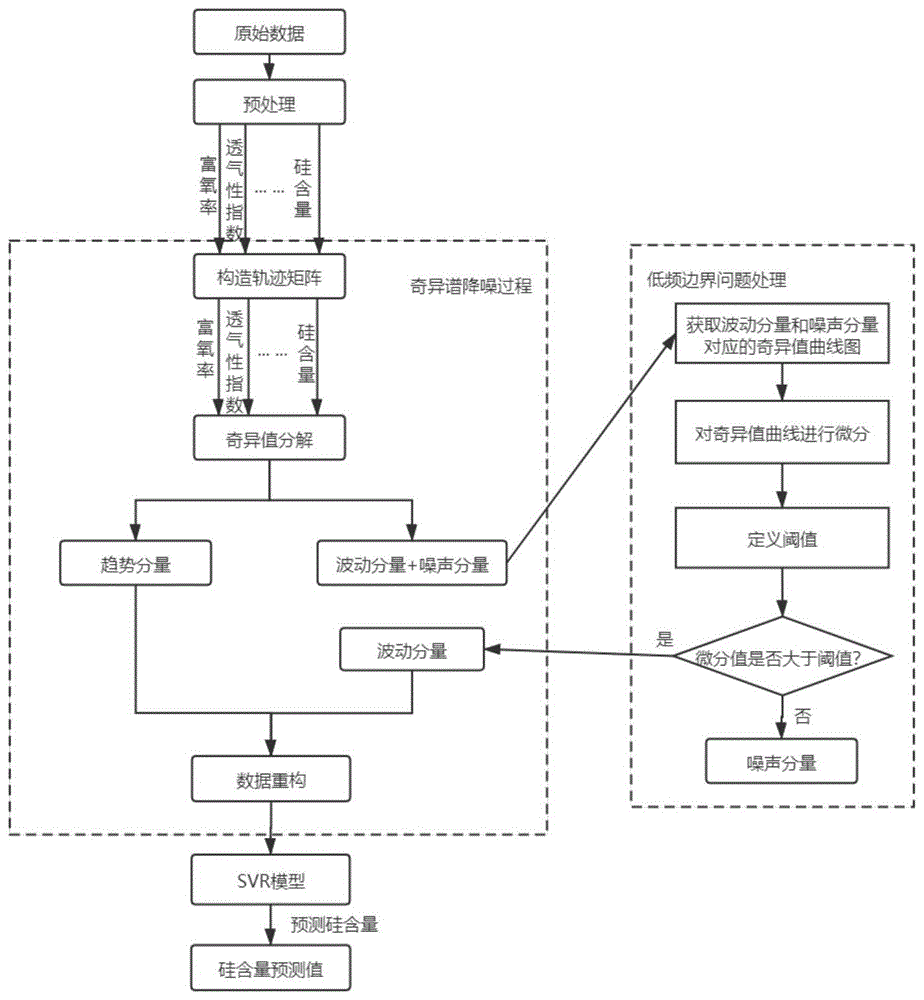
图1为本发明基于ssa-svr模型的高炉铁水硅含量预测方法的流程图；

图2为本发明实施例采集的部分原始数据表；

图3为本发明实施例的奇异值曲线图；

图4为本发明实施例的奇异值斜率变化曲线图；

图5为本发明实施例的趋势分量重构图；

图6为本发明实施例的波动分量重构图；

图7为本发明实施例的降噪前硅含量数据图；

图8为本发明实施例的降噪后硅含量数据图；

图9为本发明实施例的ssa-svr预测模型硅含量的预测结果图。

具体实施方式

下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例用于说明本发明，但不用来限制本发明的范围。

本发明公开了一种基于ssa-svr模型的高炉铁水硅含量预测方法，如图1所示，包括以下步骤：

s1、对数据进行预处理：

选取决策属性数据即硅含量数据，及与硅含量相关的条件属性数据，对于数据中含有缺失值的现象，采取人工筛选进行取值；同时，为了消除量纲的影响，对数据进行归一化处理，并获得模型所需要的训练数据集和测试数据集。

实施例一以国内某钢铁厂2650m³高炉为应用对象，选取2017年10月，共735条数据。该数据包含富氧率，透气性指数，标准风速，冷风流量，鼓风动能，顶压，富氧压力，全压差，理论燃烧温度等15种指标数据，以及其对应的硅含量数据。本文采用粗糙集对15种指标数据进行约简，选取出与硅含量相关的11种指标建立ssa-svr预测模型，包括富氧率，透气性指数，标准风速，鼓风动能，炉富煤气量，炉富煤气量指数，理论燃烧温度，冷风压力，热风压力，实际风速，以及热风温度，这11种指标数据为条件属性数据，硅含量数据为决策属性数据，条件属性数据和决策属性数据的部分采集数据如图2所示，按步骤s1进行预处理后，对736条数据按照8:2的比例划分训练数据集和测试数据集。

s2、经奇异谱分析/ssa方法进行数据降噪；由于数据采集是处于复杂多变的工业现场，导致数据中含有噪声，因此采用奇异谱分析/ssa方法对数据进行降噪处理：将所述训练数据集的一种条件属性数据分解为独立的具有解释性的分量，包括趋势分量、波动分量和噪声分量，然后基于改进的奇异谱分析判决方法去除噪声分量，将趋势分量和波动分量重构为去噪数据集，再对所述训练数据集中的其它条件属性数据重复步骤s2。此过程可分为两个阶段：分解分量和分量重构，即

s2.1、分解分量：将所述训练数据集的一种条件属性数据，分别分解为独立的具有解释性的分量，包括趋势分量、波动分量和噪声分量；此过程又可分为两个阶段：构造轨迹矩阵和奇异值分解(svd)；

s2.1.1、构造轨迹矩阵：

假设有一维时间序列数据y(t)＝{y1,y2,…,yn}表示一种条件属性数据的训练数据集，子项yk表示一种条件属性数据的训练数据集的原始数据，k＝1,2,…,n，选择合适的窗口长度l(2≤l≤n)，将y(t)转化为轨迹矩阵：

其中k＝n-l+1，n为训练数据集的数据总个数。

在实施例一中，n＝589，以一天24小时作为一个周期，选择窗口长度l＝24，k＝565，yk表示富氧率，透气性指数，标准风速，鼓风动能，炉富煤气量，炉富煤气量指数，理论燃烧温度，冷风压力，热风压力，实际风速，以及热风温度中的一种条件属性数据的训练数据集数据。

s2.1.2、奇异值分解(svd)：

在这一步骤中，采用协方差矩阵s＝xx^t，然后利用s的奇异值分解方法生成一系列奇异值(特征值)λ1，λ2，…，λl以及对应的一系列特征向量u1，u2，…，ul，从l个奇异值中选出d个不为0的奇异值，则轨迹矩阵可重写为：

x＝x1+x2+…+xd，0<d≤l

其中，i＝1,2,…,d，λi、ui分别为奇异值及其对应的特征向量，向量vi为主成分向量。

对所述条件属性数据及其对应的硅含量数据进行svd分解，在这一阶段，奇异谱分析ssa只需要考虑窗口长度l这一参数。

s2.2、分量重构：去除噪声分量，将趋势分量和波动分量重构为去噪数据集；此过程也可分为两个阶段：分组和重构；

s2.2.1、分组：

进行奇异值分解后，将得到的式子分解为若干组，并在这些组中求和。具体来说就是，将(1,2，…,d)分解为m个不相交的组(i1，i2，…，im)。假设i＝{i1,i2,…,ir}，m×r＝d，则每个xi可分解为：因此，

在此分组过程中，需要能准确分辨出每个奇异值所代表的分量类型，也就是说，它属于趋势分量，还是波动分量或者噪声分量。由于奇异值的大小代表了该奇异值所对应的特征向量对原始序列的贡献高低。即奇异值越大，其对应的特征向量所含信息越高，即奇异值越大，其对应的特征向量越重要，越不能被摒弃。

通常，第一个奇异值代表原始数据的变化趋势，即为趋势分量。后面的奇异值则包含了波动分量与噪声分量，并且越到后面，低频信号越强，噪声分量越明显。但是，很多奇异值的大小相差并不是很大，也就是说它们之间的相关性很强，属于同一种类型分量概率很大，导致波动与噪声的界限(即中低频边界)十分模糊。因此，提出了一种改进的奇异谱分析判决方法来解决低频边界选择问题，包括以下步骤：

s2.2.1.1、构建奇异值曲线图；

s2.2.1.2、对不包含第一个奇异值部分的奇异值曲线进行微分，获得奇异值斜率变化曲线f(λi)；

s2.2.1.3、设置阈值a，若f(λi)>a，则表明第i个奇异值属于波动分量，否则属于噪声分量。

该方法采用求导的方式量化波动分量与噪声分量之间的区别，这样可以避免在对每个属性数据进行降噪时标准不统一的问题，同时，微分方法可以较好分辨波动分量与噪声分量之间的差异。当出现斜率小于a的值时，即可判定此奇异值代表噪声。

实施例一的奇异值曲线如图3所示，横轴为奇异值数，表示第i个奇异值，纵轴为奇异值λi；不包含第一个奇异值部分的奇异值斜率变化曲线如图4所示，横轴为奇异值数，纵轴为奇异值斜率；经过多次试验，设置导数阈值a为0.5时效果最佳，因此，当出现斜率小于0.5的值时，即可判定此奇异值代表噪声分量，从图4中可以看出前四个点可以判定为包含波动分量的奇异值。

s2.2.2、重构：

通过对角平均，通过如下公式将每一个xi转为一个时间序列，该时间序列是初始时间序列的一个和分量。

其中，yk^*为该时间序列的子项，表示一种条件属性数据的训练数据集的重构数据，k＝1,2,…,n，zpq表示一个(l×k)的对角平均转移矩阵z的每一个元素，1≤p≤l，1≤q≤k，

l^*＝min(l,k),k^*＝max(l,k),n＝k+l-1。

实施例一的趋势分量和波动分量通过重构公式得到的重构图分别如图5和图6所示，横轴为所述训练数据集的数据条数，纵轴为对应的趋势分量值和波动分量值；

为了验证降噪结果的效果，采用以下公式对其进行验证：

其中，yk代表原始数据，yk^*代表重构数据；snr代表信噪比，其值越低表示噪声越高，通过增加信噪比的值，可以减少信号中的噪声，n为测试数据集的数据总个数，n＝147；mse是均方误差，其值越小越好，n为训练数据集的数据总个数，n＝589；psnr是峰值信噪比，其值越大越好。

图7和图8分别为实施例一的降噪前和降噪后的硅含量数据对比图，横轴为所述训练数据集的数据条数，纵轴为硅的百分含量，信噪比snr为25.5822，峰值信噪比psnr为31.0310，均方误差mse为0.0007。

s3、svr建模与优化；建立svr预测模型，并利用十字交叉算法对svr参数寻优，将得到的最佳参数传递给svr预测模型；

s3.1、基于支持向量机回归建立svr预测模型：将条件属性数据作为所述svr预测模型的输入向量，将决策属性数据作为所述svr预测模型的输出向量；

s3.1.1、设置所述svr预测模型的输入量为条件属性数据xt，设置所述svr预测模型的输出向量为对应条件属性数据xt的决策属性数据yt，其中t＝1,2,3…,n；

s3.1.2、将所述的条件属性数据xt和所述的决策属性数据yt构成数据集(xt,yt)并采用非线性映射核函数将数据映射到高维空间，构成所述svr预测模型函数：

其中，w是高维空间元素，是非线性映射函数，b为svr预测模型阈值；

s3.1.3、引入非负的松弛变量和拉格朗日函数，利用库恩塔克条件(kkt)条件，可将svr预测模型函数f(x)写为：

其中，αt，αt^*是拉格朗日乘子，k(xt,x)是核函数，n为训练数据集的数据总个数；

s3.1.4、确定所述svr模型的核函数为高斯核函数建立所述svr模型：

其中，σ为高斯核函数的带宽；

s3.2、对所述svr模型执行十字交叉算法，求解svr预测模型的最佳参数；

s3.3、将上述求得的最佳参数传递给svr预测模型，训练样本数据建立最佳svr预测模型。

实施例一采用径向基函数作为支持向量机回归的核函数，并采用交叉验证结合网格搜索法寻找最佳参数，选取c＝4.7，σ＝0.0278，c为支持向量机回归中的惩罚参数，建立最佳svr预测模型，预测结果如图9所示，横轴为所述测试数据集的数据条数，纵轴为硅的百分含量。

为了能进一步定量地看出预测结果和性能，本发明采用了几种传统的统计方法，平均绝对误差mae，均方误差mse，此外，还计算了误差在±0.1％内的准确率。

其中，y′t为模型预测值yt对应的实际值，n为测试数据集的数据总个数，n＝147，经计算，预测误差在0.1％内准确率为93.88％，平均绝对误差mae为0.0405，均方误差mse为0.0029，因此，预测模型的硅含量预测值较为准确。

s4、硅含量预测：利用训练数据集训练得到的所述svr预测模型对高炉铁水中的硅含量进行预测。

综上可知，通过上述的一种基于ssa-svr的高炉铁水硅含量预测方法，具有以下优点：

(1)本发明解决了异常数据和含有噪声数据导致的建模不可靠的问题，将奇异谱分析ssa方法引入高炉冶炼数据处理，将数据分解为趋势分量、波动分量以及噪声分量，在保留有效数据分量的前提下，去除噪声分量，大大降低了建立不可靠模型的风险，能有效防止预测模型出现过拟合、甚至不稳定的现象，提高预测模型的准确度；

(2)本发明提出了一种改进的奇异谱分析判决方法，该方法对奇异值曲线进行微分，建立奇异值斜率变化曲线图，并定义阈值，实现噪声分量与波动分量分割的稳定性，有效区分波动分量和噪声分量，提高了降噪的有效性，避免传统人为选择的随意性与不确定性，从而提高预测模型的精确性；

(3)本发明基于支持向量机回归建立svr模型能够很好地作用于非线性系统，具有良好的泛化能力。

最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；虽然结合附图描述了本发明的实施方式，但是本领域技术人员可以在不脱离本发明的精神和范围的情况下做出各种修改和变型，这样的修改和变型均落入由所附权利要求所限定的范围之内。