基于模糊随机参数的裕度与不确定性量化结构可靠性评估方法与流程

本发明涉及到一种基于模糊随机参数的裕度与不确定性量化(qualificationandmarginofuncertainty,qmu)结构可靠性评估方法，旨在对同时含有固有不确定性和认知不确定性信息的结构进行可靠性评估，属于结构可靠性分析领域。
背景技术：
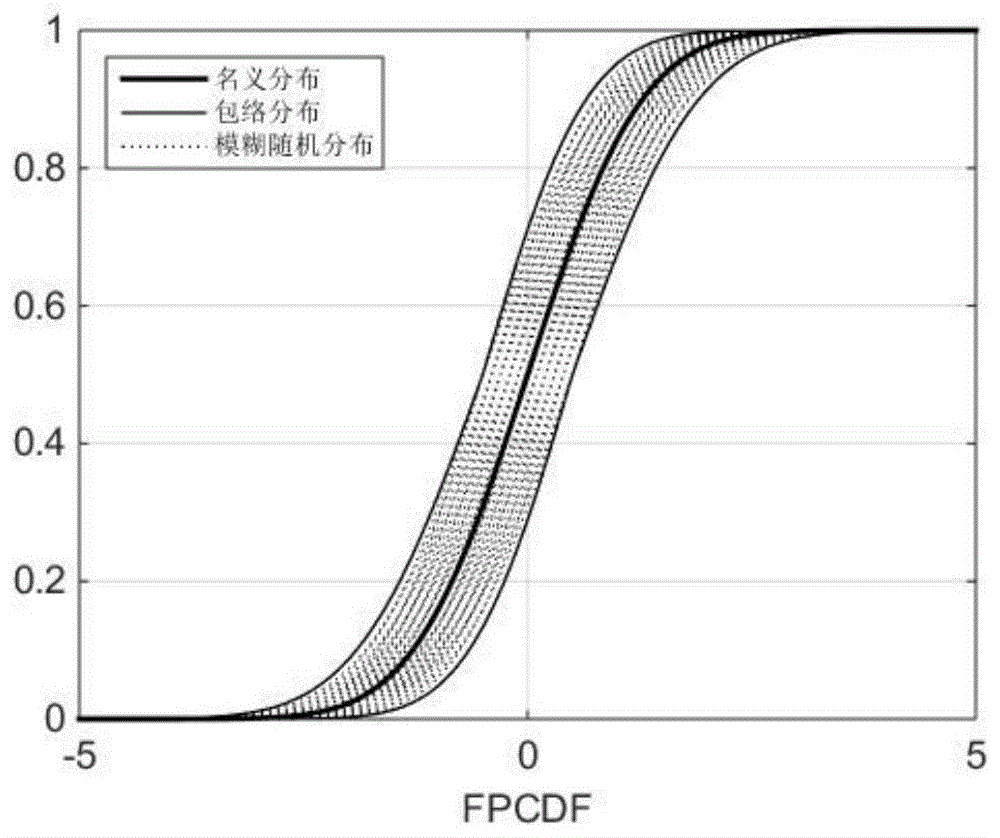
：第一个方面，对于统计数据不足和样本量较小的复杂系统或结构，传统的可靠度求解方法很难计算和表征其可靠度。美国于1992年停止核武器全系统试验之后，由于实验数据和不确定性的限制，军方需要一种不依赖于试验和基于认知不确定性的可靠性评估方法，因此，基于裕度与不确定性量化(qmu)的可靠性评估方法应运而生，洛斯阿拉莫斯国家实验室、劳伦斯利弗莫尔国家实验室和桑迪亚国家实验室应军方要求于2002年提出了一整套完整的qmu方法，并将其定义为“在不确定条件下，以工程系统的性能阈值和相关裕度为中心的复杂技术决策的决策支持方法”。qmu可靠性评估最初在核武器储存可靠性、风险应对和安全认证中得到了广泛的应用。随着其对统计数据不充分和小子样问题处理的高效性和可操作性日益突显，最近的研究集中在结构风险评估和复杂系统评估等问题中。在qmu中，设计点是指设备在标称工作条件下的响应，也叫理论设计输出值，即广义响应；设计工作范围是指由包含设计点的固有不确定性或公差产生的范围；性能通道是指由响应上限和下限组成的间隔，响应上限和下限对应于可靠边界，即广义强度；性能裕度m(margin)是指设计工作范围下限与性能通道上限之间的距离；不确定度u(uncertainty)是指由认知不确定度引起的响应波动范围；置信系数cf＝m/u(confidencefactor)是指对性能的可靠性进行评判。当cf＞1对应于性能可靠或可接受，cf≤1对应于故障或风险，cf的大小衡量了可靠/失效的程度，它是一种在有限数据可用性下的系统性能置信度度量。目前qmu方法考虑了各种不确定性理论。包括概率框架下的qmu(probabilityqmu)，基于证据理论的qmu方法，区间分析和证据理论混合下的qmu方法，基于概率盒的qmu方法等。qmu理论对信息不完备导致描述不清晰的对象进行可靠性评估，将cf作为可靠性指标可以直观地表征含有认知类信息对象的可靠程度，因此利用qmu理论来处理非概率信息下的可靠性评估问题具有一定的优势。但在目前研究的qmu理论体系中，缺少一种同时考虑固有随机分布和基于分布参数的认知不确定性下的方法，而在工程实际中，有些设计参数的统计数据完全掌握，而有些数据并不完备，因此包含两类信息的情况广泛存在。第二个方面，模糊随机变量作为兼具固有和认知不确定性特征的不确定性变量，不同于概率盒的单一固有不确定性的函数族表达，也不同于证据理论繁冗地在每个区间分段上进行概率分配，它是一个连续的函数表达式，具有概率分布的形式，但分布参数为模糊数，模糊随机变量融合了随机分布和不完全信息的特征，表征简洁。模糊随机变量以其独特的性质在可靠性算法中得到了广泛的应用。包括基于模糊随机变量的模糊一阶可靠性方法fform(fuzzyfirstorderreliabilitymethod)、基于系统的时变可靠性问题鞍点逼近法、基于模糊随机变量理论的模糊蒙特卡罗模拟、基于模糊随机变量的区间有限元法和基于模糊随机数据下的贝叶斯方法等。基于以上两个方面，本发明提出一种基于模糊随机参数的裕度(亦称：裕量)与不确定性量化结构可靠性评估方法。技术实现要素：(一)本发明的目的本发明的目的在于，采用裕度与不确定性量化(qmu)方法将模糊随机变量应用于结构可靠性评估，旨在探索一种新的固有与认知混合不确定性下的qmu可靠性评估框架。由于模糊随机变量的参数在每个截集上的有不同的隶属度区间范围，需要对每个截集下的性能裕度和不确定度进行求解。本发明采用基于包络分布的二次四阶矩法确定结构性能输出的边界，其中用到了最大熵模型(me,maximumentropy)来拟合结构响应的模糊概率密度函数fpdf(fuzzyprobabilitydensityfunction)。(二)技术方案本发明为实现上述目的，采用如下技术方案：本发明一种基于模糊随机参数的裕度与不确定性量化结构可靠性评估方法，它涉及到一种基于模糊随机参数的裕量与不确定性量化(qualificationandmarginofuncertainty,qmu)结构可靠性评估方法，其实施步骤如下：步骤(1)、确定结构的模糊随机变量和置信度γ，初始化截集α＝0；步骤(2)、构造各个模糊随机变量在当前截集下的包络分布；步骤(3)、根据模糊随机变量的包络分布，抽样并计算包络分布的前4阶中心距μxi,i＝0,1,2,3,；4步骤(4)、对结构响应函数在名义分布的均值点处进行泰勒级数展开至前2次，并以包络分布前4阶中心距为基础，结合结构响应函数推导得到结构响应边界的前4阶中心距步骤(5)、基于最大熵方法，以结构响应边界的前4阶中心距为约束，拟合出结构响应边界的fpdf多项式的系数aj,j＝0,1,2,3，,4从而得到结构响应fpdf边界表达式步骤(6)、根据给定的置信度，计算α截集下的裕度mα：mα为阈值与结构响应的模糊概率累计分布函数fpcdf(fuzzyprobabilitycumulativedistributionfunction)边界在置信度为0.5的值之差，fpcdf为步骤(5)中fpdf表达式积分结果；计算α截集下的结构响应不确定度uα：uα为结构响应的模糊概率累计分布函数fpcdf在给定置信度下的值与结构响应名义响应的概率累计分布函数cdf(cumulativedistributionfunction)在置信度为0.5的值之差；步骤(7)、根据mα和uα计算α截集下的置信系数cfα＝mα/uα；判断α＜1，若是，增量α＝α+δα，回到步骤(2)；否则，进行步骤(8)；步骤(8)、根据qmu定义，计算结构整体可靠性评估结果cf＝min{cfα},α∈[0,1]。其中，在步骤(1)中所述的“模糊随机变量”，是指基本分布为随机变量，但分布参数为模糊数的不确定变量，以模糊随机正态分布为例：设和分别是模糊随机变量的模糊均值和模糊标准差，则模糊随机正态分布可表示为其中，在步骤(1)中所述的“确定结构的模糊随机变量和置信度γ，初始化截集α＝0”，其确定的过程如下：在给定结构分析对象下，根据专家经验确定结构对象中的模糊随机变量及其参数分布，模糊性；根据工程要求，给出置信度γ∈[0,1]。其中，在步骤(2)中所述的“构造各个模糊随机变量在当前截集下的包络分布”中，包络分布是由模糊随机变量fpcdf的上下边界组成的包络线；包络分布的目的是综合描述模糊随机变量的边界，并可以用统计方法求得边界的中心矩；包络分布的构造如下所示：设和分别是模糊随机变量的模糊均值和模糊标准差；所有的隶属函数都假定为模糊三角数；因此，模糊平均值和标准差可以分别表示为和其中上标l、m和u分别为下界、中界和上界；在给定的α截集下，模糊随机变量fpcdf上(下)界的阶矩可通过以下操作得到：在均值区间和标准差区间得到后，fpcdf上界的样本点由由两部分组成：在的左侧以为分布进行抽样，在的右侧以为分布进行抽样，上界采样点集被定义为相对应的，fpcdf下界是在的左侧以为分布进行抽样，在的右侧以为分布进行抽样，下界采样点集被定义xα＝{x1,x2，...,xn}；因此，fpcdf上、下界的各阶矩可分别根据和xα运用数理统计方法快速得到；特别地，对服从x～n(μm,σm)的分布称为名义分布；图1给出了和的模糊随机变量的包络分布和名义分布示意图。其中，在步骤(3)中所述的“抽样并计算包络分布的前4阶中心距”，是指对步骤(2)中的进行中心距计算，第k阶中心距计算公式为：其中，在步骤(3)中所述的“根据模糊随机变量的包络分布，抽样并计算包络分布的前4阶中心距μxi,i＝0,1,2,3,4”，其作法如下：μx0＝1当求解包络分布上界的前4阶中心距时，上式中的xi为从步骤(2)所求抽样点集中抽取的样本点，样本点数为n；当求解包络分布下界的前4阶中心距时，上式中的xi为从步骤(2)所求抽样点集xα中抽取的样本点，样本点数为n。其中，在步骤(4)中所述的“对结构响应函数在名义分布的均值点处进行泰勒级数展开至前2次”是指：假设结构响应函数为其中为模糊随机变量；针对在α截集下结构响应的fcdf上(下)界在名义分布的均值点对进行前两个数量级的泰勒近似展开：其中，在步骤(4)中所述的“对结构响应函数在名义分布的均值点处进行泰勒级数展开至前2次，并以包络分布前4阶中心距为基础，结合结构响应函数推导得到结构响应边界的前4阶中心距其作法如下：根据步骤(3)中得到的fpcdf边界的前4阶矩并结合上式(已得到的前2次泰勒级数展开式)，按以下公式得到结构响应的一阶至四阶中心距和当计算结构响应上界的一阶至四阶中心距时，zq即当计算结构响应下界的一阶至四阶中心距时，zq即其中，在步骤(5)中所述的“基于最大熵方法，以结构响应边界的前4阶中心距为约束，拟合出结构响应边界的fpdf多项式的系数aj,j＝0,1,2,3,4，从而得到结构响应fpdf边界表达式是指：以求解结构响应上边界的为例，α截集下的最大熵模型可以表示如下(下边界同理)：其中，c为常数，为标准化；采用拉格朗日乘子法求解最大熵模型：λi,i＝0,1,2,3,4为拉格朗日待定系数，则结构响应函数的近似表达式可简化如下：其中，a0＝1-λ0/c，ai＝-λ0/c(i＝1,2,3,4)；另一方面，α截集下前四阶矩已在中推导得到，则结构响应函数的近似表达式可求解。其中，在步骤(6)中所述的“根据给定的置信度，计算α截集下的裕度mα”和“计算α截集下的结构响应不确定度uα”，是指：在给定截集水平下，mα为步骤(5)中求出的结构响应函数上边界在置信度为0.5时的点yfunction和阈值fth之差；不确定度uα为步骤(5)中求出的结构响应函数上边界在置信度为(1+γ)/2时的点(ufunction)α和名义响应在置信度为0.5时的点u0.5之差；名义响应是指结构响应函数在模糊随机变量名义分布下的输出；m和u的计算公式可表示为：mα＝fth-(yfunction)α；uα＝(ufunction)α-u0.5在案例中，为方便理解，fth，(yfunction)α，(ufunction)α和u0.5分别被标记为margin_up，margin_low，ucertainty_up和uncertainty_low。其中，在步骤(7)中所述的“根据mα和uα计算α截集下的置信系数cfα＝mα/uα”，是指根据步骤(6)的计算结果，按照下式计算本截集下fqmu指标：mα和uα为步骤(6)中计算结果。其中，在步骤(8)中所述的“根据qmu定义，计算结构整体可靠性评估结果cf＝min{cfα},α∈[0,1]”，是指在所有截集下cfα求出之后，按照以下公式计算结构整体可靠性评估结果：cf＝min{cfα},α∈[0,1]基于模糊随机变量的qmu可靠性评估示意图和流程图分别见图2和图3所示。(三)本发明的优点和功效本发明所述的结构可靠性评估方法，结合qmu和模糊随机变量的各自特点，提出新的qmu指标的计算框架，其优点和功效在于：(1)它构建了混合不确定性下的qmu可靠性评估指标，能很好地描述模糊随机变量输入下的可靠性评估输出，能够指导不完全数据下的可靠性评估；(2)它计算方便快捷，能表示整个结构的qmu度量，也能表示不同截集下的度量，提供了不同认知水平下的可靠性评估表征；(3)它既考虑了qmu的原始定义，又考虑了模糊数的特点，同时也是一种混合不确定性量化与传播的计算框架；(4)本发明所述的可靠性评估方法科学，工艺性好，具有广阔推广应用价值。附图说明(图中序号、符号、代号说明如下)图1、模糊概率累计分布函数。图2、基于模糊随机变量的qmu可靠性评估指标。图3、本发明所述可靠性评估方法流程图。图4、自由梁受力图。图5、x1和x2模糊概率累计分布函数。图6、自由粱qmu可靠性评估示意图。图7、桁架受力图。图8、x1，x2，x3和x4模糊概率累计分布函数。图9、桁架qmu可靠性评估示意图。图中序号、符号、代号说明如下:图1中，fpcdf为模糊概率累计分布函数。图2中，fpcdf为模糊概率累计分布函数，γ为置信度，p为置信度边界，m为性能裕度，yfunction为结构响应边界，fth为阈值。图6中，uncertainty_up为不确定度上界，uncertainty_low为不确定度下界，mrgin_low为性能裕度下界。图7中，a、b、c、d、e、f和g为桁架定点标识。l为混凝土和钢筋长度。图9中，uncertainty_up为不确定度上界，uncertainty_low为不确定度下界，mrgin_low为性能裕度下界。本说明书所涉及到的符号、代号补充说明如下:qmu(qualificationandmarginofuncertainty)--裕度与不确定性量化cf＝m/u(confidencefactor)--置信系数fform(fuzzyfirstorderreliabilitymethod)--基于模糊随机变量的模糊一阶可靠性方法me(maximumentropy)--最大熵模型fpdf(fuzzyprobabilitydensityfunction)--模糊概率密度函数fpcdf(fuzzyprobabilitycumulativedistributionfunction)--模糊概率累计分布函数cdf(cumulativedistributionfunction)--概率累计分布函数具体实施方式下面结合算例和附图对发明的技术方案进行详细的说明。案例1：承受均匀荷载的自由支撑梁如图4所示。长度l、断面宽度b、断面高度h均为基本变量，即l＝4000mm，b＝105mm，h＝210mm，为模糊随机变量，其分布形式为正态分布，即其均值mean和标准差std为模糊数，隶属函数如图5所示。梁的材料为45号钢，其强度为850mpa。根据材料力学的基本理论，自由支撑梁的最大应力为：置信度取0.9，截集增量δα取0.2，运用本专利方法对其进行可靠度评估，过程如下：本发明一种基于模糊随机参数的裕度与不确定性量化结构可靠性评估方法，如图3所示，其实施步骤如下：步骤(1)、确定结构的模糊随机变量，初始化截集α＝0；步骤(2)、构造各个模糊随机变量在当前截集下的包络分布，如包络分布示意图1见图5所示；步骤(3)、根据模糊随机变量的包络分布，抽样并计算包络分布的前4阶中心距，结果如下；表1x1fpdf上界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝0199.99724.45930.00182.9920α＝0.2204.03174.49090.04553.0230α＝0.4208.07234.46820.04502.9850α＝0.6212.11174.48100.06553.0006α＝0.8216.14454.46590.10913.0012α＝1.0220.18504.46110.11003.0220表2x1fpdf下界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝0199.99024.4813-0.00223.0215α＝0.2195.97424.4804-0.04033.0102α＝0.4191.92344.4758-0.05162.9899α＝0.6187.90364.4817-0.07742.9944α＝0.8183.87014.4729-0.09112.9944α＝1.0179.81094.4697-0.12312.9997表3x2fpdf上界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝0105.00213.1746-0.00232.9932α＝0.2108.03433.15930.02442.9970α＝0.4111.04513.16020.04973.0177α＝0.6114.08313.16590.06992.9930α＝0.8117.09273.16420.10032.9982α＝1.0120.12813.15690.12453.0362表4x2fpdf下界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝0105.00443.16690.00932.9986α＝0.2101.97883.1584-0.01053.0039α＝0.498.96843.1561-0.06283.0090α＝0.695.91073.1458-0.08422.9982α＝0.892.90893.1542-0.09453.0155α＝1.089.87553.1546-0.10742.9959步骤(4)、对结构响应函数在名义分布的均值点处进行泰勒级数展开至前2次，并以包络分布前4阶中心距为基础，结合结构响应函数推导得到结构响应边界的前4阶中心距；表5结构响应fpdf上界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝0523.0672.1190.392572.915α＝0.2518.2969.8940.382242.9443α＝0.4513.9967.3130.367852.9536α＝0.6509.8365.5230.358772.9655α＝0.8505.9663.2750.358652.9835α＝1.0502.1961.2110.34453.0098表6结构响应fpdf下界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝0522.9872.2740.383682.9312α＝0.2527.9274.6220.385142.9148α＝0.4533.0377.3180.408792.8764α＝0.6538.7380.1480.414012.8583α＝0.8544.6983.320.43422.8457α＝1.0551.0786.6730.442342.8257步骤(5)、基于最大熵方法，以结构响应边界的前4阶中心距为约束，拟合出结构响应边界的fpdf多项式的系数aj,j＝0,1,2,3,4，从而得到结构响应fpdf边界表达式表7结构响应fpdf上界表达式截集四次项系数三次项系数二次项系数一次项系数常数项α＝0-0.404530.10742-0.027225-0.27951-0.95921α＝0.2-0.418880.099248-0.023438-0.26191-0.95279α＝0.4-0.426740.092331-0.021026-0.24606-0.94945α＝0.6-0.433560.087511-0.019143-0.23506-0.94646α＝0.8-0.439460.085566-0.017861-0.23107-0.94367α＝1.0-0.451620.077885*-0.014723-0.21337-0.93821表8结构响应fpdf下界表达式截集四次项系数三次项系数二次项系数一次项系数常数项α＝0-0.024690.10147-0.41366-0.26652-0.95519α＝0.2-0.0262730.10418-0.40703-0.27208-0.95824α＝0.4-0.0331610.12045-0.38308-0.30711-0.9687α＝0.6-0.0358410.12584-0.37326-0.31817-0.97306α＝0.8-0.0405920.13863-0.35926-0.34538-0.97893α＝1.0-0.0444420.14683-0.34627-0.36186-0.9846步骤(6)、根据给定的置信度，计算α截集下的裕度mα和结构响应不确定度uα；如基于模糊随机变量的qmu可靠性评估示意图图2见图6所示(α＝1时)，在每一截集下的计算结果见表9所示。表9mα和uα在各截集下的计算结果截集margin_upmargin_lowuncertainty_upuncertainty_lowα＝0850517.2652.35520α＝0.2850521.95661.49520α＝0.4850526.07672.98520α＝0.6850531.52683.8520α＝0.8850536.36698.83520α＝1.0850542.41711.42520步骤(7)、根据mα和uα计算α截集下的置信系数cfα＝mα/uα。判断α＜1，若是，增量α＝α+δα，回到步骤(12)；否则，进行步骤(8)；fqmu在各截集计算结果如下所示；表10fqmu结果截集fqmuα＝02.514545α＝0.22.318538α＝0.42.117466α＝0.61.944322α＝0.81.753844α＝1.01.606885步骤(8)、根据qmu定义，计算结构整体可靠性评估结果cf＝min{cfα},α∈[0,1]。cf＝min{2.5145,2.3185,？2.1175,1.9443,1.7538,1.6069}＝1.6069。案例2：屋顶桁架如图7所示，顶部吊杆和压杆用混凝土加固，底部吊杆和拉杆用钢制成。该评估是在假定屋架承受均布荷载，且均布荷载q可转化为节点荷载的前提下进行的p＝ql/4。节点的垂直位移可以通过力学分析得到，它可以表示成基本变量的函数，即其中，ac，as，ec，es和l分别是混凝土横截面积、钢筋横截面积、混凝土弹性模量、钢筋弹性模量和混凝土(钢筋)长度。按照安全性和可靠性的要求，顶点c在垂直方向的位移阈值为3.1cm，并可利用该条件构造极限状态函数。l＝12m，q＝2×104n。在本例中，ac，as，ec和es为模糊随机正态分布。变量的均值μ和标准差σ设为三角模糊数：α在0到1之间变化，在以下α下评估模糊数：0.0、0.2、0.4、0.6、0.8和1.0。置信度取0.95，截集增量δα取0.2，运用本专利方法对其进行可靠度评估，过程如下：本发明一种基于模糊随机参数的裕度与不确定性量化结构可靠性评估方法，如图3所示，其实施步骤如下：步骤(1)、确定结构的模糊随机变量，初始化截集α＝0；步骤(2)、构造各个模糊随机变量在当前截集下的包络分布，如包络分布示意图1见图8所示；步骤(3)、根据模糊随机变量的包络分布，抽样并计算包络分布的前4阶中心距，结果如下；表11x1fpdf上界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝00.25000.1414-0.00142.9976α＝0.20.25280.14140.02213.0069α＝0.40.25640.14150.04913.0027α＝0.60.25950.14150.07313.0018α＝0.80.26230.14130.09403.0024α＝1.00.26580.14130.11733.0231表12x1fpdf下界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝00.25000.14150.00022.9977α＝0.20.24720.1413-0.01912.9935α＝0.40.24370.1415-0.04762.9969α＝0.60.24060.1413-0.07153.0011α＝0.80.23750.1411-0.09533.0026α＝1.00.23450.1413-0.12033.0176表13x2fpdf上界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝00.99980.2447-0.00033.0019α＝0.21.00340.24500.01962.9995α＝0.41.00730.24480.04033.0056α＝0.61.01050.24480.05592.9992α＝0.81.01440.24510.07902.9950α＝1.01.01810.24490.10273.0089表14x2fpdf下界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝01.00000.24510.00363.0031α＝0.20.99640.2450-0.02012.9973α＝0.40.99280.2449-0.03992.9965α＝0.60.98910.2450-0.05973.0068α＝0.80.98560.2448-0.07823.0024α＝1.00.98200.2447-0.09493.0012表15x3fpdf上界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝00.59990.2236-0.00143.0019α＝0.20.60400.22350.02483.0101α＝0.40.60770.22340.04823.0023α＝0.60.61130.22380.07162.9976α＝0.80.61510.22330.09683.0033α＝1.00.61900.22340.11743.0086表16x3fpdf下界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝00.60010.22330.00023.0101α＝0.20.59620.2234-0.02372.9953α＝0.40.59260.2236-0.04522.9978α＝0.60.58840.2233-0.06932.9942α＝0.80.58500.2234-0.09903.0103α＝1.00.58100.2234-0.11583.0156表17x4fpdf上界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝01.10030.22340.00642.9918α＝0.21.10390.22350.02433.0040α＝0.41.10750.22350.04812.9964α＝0.61.11100.22370.07103.0053α＝0.81.11520.22360.09523.0064α＝1.01.11890.22330.12183.0139表18x4fpdf下界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝01.09990.22360.00062.9964α＝0.21.09600.2235-0.02473.0033α＝0.41.09240.2238-0.05243.0028α＝0.61.08840.2236-0.07382.9996α＝0.81.08480.2235-0.09443.0065α＝1.01.08090.2234-0.11943.0095步骤(4)、对结构响应函数在名义分布的均值点处进行泰勒级数展开至前2次，并以包络分布前4阶中心距为基础，结合结构响应函数推导得到结构响应边界的前4阶中心距；表19结构响应fpdf上界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝02.61280.164830.0903452.988α＝0.22.64020.165930.100952.9889α＝0.42.67010.166770.112392.9893α＝0.62.69690.167750.122282.9886α＝0.82.7260.168610.134012.9883α＝1.02.75640.169370.145952.992表20结构响应fpdf下界前四阶中心距截集一阶中心距矩二阶中心距矩三阶中心距矩四阶中心距矩α＝02.61290.16510.0910392.9887α＝0.22.58560.164030.0788312.9875α＝0.42.55720.163330.0674012.9873α＝0.62.52830.162250.0563722.9889α＝0.82.50190.161130.0454822.9888α＝1.02.47460.160230.0354462.9892步骤(5)、基于最大熵方法，以结构响应边界的前4阶中心距为约束，拟合出结构响应边界的fpdf多项式的系数aj,j＝0,1,2,3,4，从而得到结构响应fpdf边界表达式表21结构响应fpdf上界表达式截集四次项系数三次项系数二次项系数一次项系数常数项α＝0-0.001540.015753-0.49293-0.046701-0.92212α＝0.2-0.00175460.017693-0.49219-0.052372-0.92241α＝0.4-0.00204420.019841-0.49112-0.058605-0.92284α＝0.6-0.00237320.022005-0.48989-0.064841-0.92334α＝0.8-0.00271150.023939-0.48858-0.070372-0.92389α＝1.0-0.00301480.02627-0.48769-0.077056-0.9242表22结构响应fpdf下界表达式截集四次项系数三次项系数二次项系数一次项系数常数项α＝0-0.00152350.015863-0.49306-0.047035-0.92205α＝0.2-0.00131740.013668-0.49374-0.04059-0.9218α＝0.4-0.00111590.011626-0.49451-0.034577-0.92149α＝0.6-0.000873170.0096566-0.4956-0.028773-0.921α＝0.8-0.00073410.0077624-0.49614-0.023154-0.92078α＝1.0-0.000617920.0060301-0.49663-0.018003-0.92057步骤(6)、根据给定的置信度，计算α截集下的裕度mα和结构响应不确定性uα；基于模糊随机变量的qmu可靠性评估示意图图2见图9所示(α＝1时)，在每一截集下的计算结果见表23所示。表23mα和uα在各截集下的计算结果截集margin_upmargin_lowuncertainty_upuncertainty_lowα＝03.52.61122.94412.61α＝0.23.52.64042.97592.61α＝0.43.52.66853.0072.61α＝0.63.52.69363.03582.61α＝0.83.52.72263.06832.61α＝1.03.52.7533.10022.61步骤(7)、根据mα和uα计算α截集下的置信系数cfα＝mα/uα。判断α＜1，若是，增量α＝α+δα，回到步骤(12)；否则，进行步骤(8)。fqmu在各截集计算结果如下所示；表24fqmu结果截集fqmuα＝02.660281α＝0.22.349276α＝0.42.094458α＝0.61.893847α＝0.81.696269α＝1.01.523868步骤(8)、根据qmu定义，计算结构整体可靠性评估结果cf＝min{cfα},α∈[0,1]。cf＝min{2.6603,2.3493,2.0945,1.8938,1.6963,1.5239}＝1.5239。当前第1页12