基于显性和隐性信任的协同过滤推荐方法与流程

本发明涉及推荐技术领域，特别涉及一种基于显性和隐性信任的协同过滤推荐方法。

背景技术：

社交媒体是人们现在常用交流和获取信息的重要平台。社交媒体用户可以在此平台进行关注好友、评论好友、转发评论、浏览热点新闻等。社交媒体中会记录下用户的行为数据，由于社交媒体的用户巨多，所以用户的行为信息是海量的，如新浪微博、今日头条中的关注和浏览信息，epinions(epinions是一个大众消费者点评网站)中的信任信息等。

和现实世界中相同，社交媒体中同样存在用户之间相互影响彼此的选择和相互推荐自己喜欢的。比如说现在机器学习这么火热，人们想了解“机器学习”的最新研究状况，我们通常会先了解机器学习领域中的专家们，看一下他们的课题组最近在研究的方向，跟进即可。也就是说，有些时候我们通常会去找我们相信的那些人，去看他们推荐的东西，影响我们即将采取的行为。这就说明融合社会关系的建模有利于改进推荐的质量。传统的推荐系统方法主要有基于用户的推荐、基于物品的推荐、基于内容的推荐等，由于信息密度低，信息来源单一，计算量大等系列问题，导致长时间内推荐系统推荐效果提升不高。

研究者们开始关注社交网络中融合信任关系的推荐方法。但是传统的基于信任的推荐方法仅利用简单的二值信任网络，并没有区分不同信任关系的强度，而在现实生活中即使都是朋友也有亲疏之分，因此我们应该区别对待不同强度的社会关系。后来基于社交网络中信任的研究，都只是单方面的研究显示信任和隐性信任融合推荐系统，从而使得目前的推荐方法存在由于信息过载导致的数据稀疏和用户冷启动问题，影响推荐准确性。

技术实现要素：

本发明提供了一种基于显性和隐性信任的协同过滤推荐方法，其目的是为了解决由于信息过载导致的数据稀疏和用户冷启动问题。

为了达到上述目的，本发明的实施例提供了一种基于显性和隐性信任的协同过滤推荐方法，该协同过滤推荐方法包括：

步骤1，根据用户物品评分矩阵r，计算用户u对用户v的进行预测评分时的准确性；

步骤2，计算用户u对用户v的依赖程度；

步骤3，根据所述准确性和所述依赖程度，计算用户u对用户v的隐性信任度；

步骤4，根据所述隐性信任度对用户物品评分矩阵r进行填充，得到填充处理后的用户物品评分矩阵；

步骤5，计算用户u对物品的评分置信度；

步骤6，根据所述评分置信度和填充处理后的用户物品评分矩阵，计算用户u与用户v之间的相似性；

步骤7，计算用户u的全局信任度，并计算用户u对用户v的局部信任度；

步骤8，根据所述全局信任度和所述局部信任度，计算用户u对用户v的最终信任度；

步骤9，根据所述相似性和所述最终信任度，修正用户u的潜在用户特征矩阵；

步骤10，根据所述潜在用户特征矩阵，预测用户u对物品i的评分。

本发明的上述方案至少有如下的有益效果：

在本发明的实施例中，通过充分挖掘了用户的信息，将隐性信任和显性信任融合在推荐系统中，使数据稀疏的效果更加能考虑到用户的偏好信息，缓解用户物品评分矩阵数据稀疏的问题，以及用户冷启动的问题，提高推荐准确性。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图示出的结构获得其他的附图。

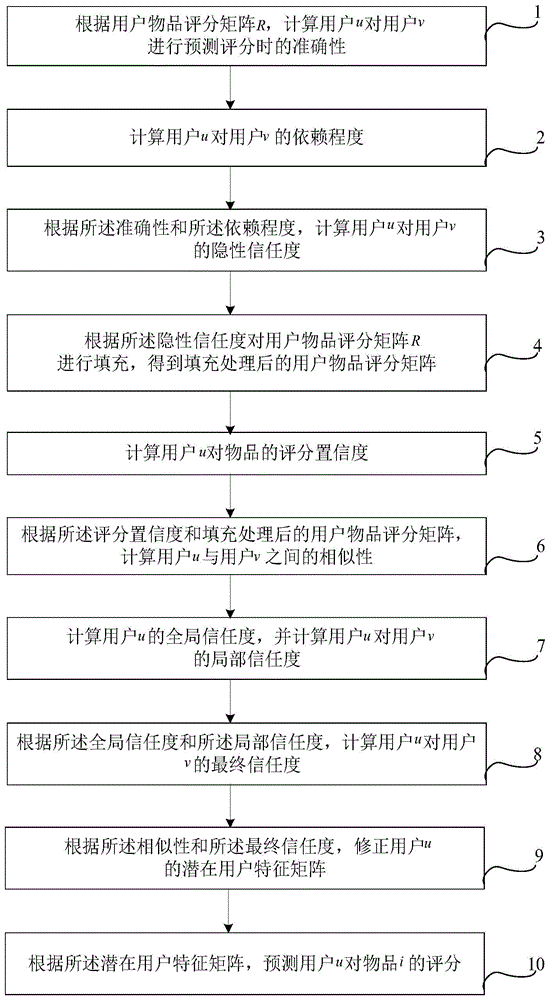
图1是本发明实施例的基于显性和隐性信任的协同过滤推荐方法的流程图；

图2是本发明实施例的验证实验中数据集的统计数据的示意图；

图3是本发明实施例的验证实验中参数的示意图；

图4是本发明实施例的验证实验中实验结果的示意图之一；

图5是本发明实施例的验证实验中实验结果的示意图之二。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

如图1所示，本发明的实施例提供了一种基于显性和隐性信任的协同过滤推荐方法，该协同过滤推荐方法包括如下步骤：

步骤1，根据用户物品评分矩阵r，计算用户u对用户v进行预测评分时的准确性。

其中，在本发明的实施例中，上述步骤1的具体实现方式可以为：通过公式计算用户u对用户v进行预测评分时的准确性。

其中，accuracy(u，v)表示用户u对用户v进行预测评分时的准确性，iuv＝iu∩iv，iuv表示用户u与用户v共同评分的物品集合，ru，i表示用户物品评分矩阵r中用户u对物品i的真实评分，rmax表示用户物品评分矩阵r中用户u对物品i的评分最大值，pu,i表示基于单一用户的评分信息计算出来的用户u对物品i的预测评分，表示在用户物品评分矩阵r中用户u评论过的物品的平均评分，表示在用户物品评分矩阵r中用户v评论过的物品的平均评分。

需要说明的是，在计算用户u对用户v进行预测评分时的准确性之前，可对预先得到的用户物品评分矩阵r进行预处理(包括但不限于删除不必要的数据等操作)，以提高准确性的计算效率。

步骤2，计算用户u对用户v的依赖程度。

其中，由于用户物品评分矩阵r数据相对来说稀疏，用户共同评分的物品少，准确性会降低，所以要计算出用户评分时数据的可依赖程度，即依赖性。

具体的，在本发明的实施例中，上述步骤2的具体实现方式可以为：

通过公式计算用户u对用户v的依赖程度。

其中，dependability(u，v)表示用户u对用户v的依赖程度，iu表示用户u已评分的物品集合，iv表示用户v已评分的物品集合。

步骤3，根据所述准确性和所述依赖程度，计算用户u对用户v的隐性信任度。

其中，在本发明的实施例中，将隐性信任综合用户评分准确性与可依赖度因素进行整体度量，使用用户间的准确性和依赖性共同表示隐性信任度。

具体的，在本发明的实施例中，上述步骤3的具体实现方式可以为：通过公式计算用户u对用户v的隐性信任度。

其中，tr^im(u，v)表示用户u对用户v的隐性信任度。由于用户总是信任自己的，用户u对用户u的信任是百分之百的，即tr^im(u，u)＝1。

步骤4，根据所述隐性信任度对用户物品评分矩阵r进行填充，得到填充处理后的用户物品评分矩阵。

其中，在本发明的实施例中，根据步骤3计算出来的隐性信任度，对用户物品评分矩阵进行数据的填充，能使用户的偏好更加准确。

具体的，在本发明的实施例中，上述步骤4的具体实现方式可以为：

定义隐性信任邻居集合tn^im，给定用户u，若使tr^im(u,v)＞0，则称用户v为用户u的隐性信任邻居，用户u的隐性信任邻居集合为其中,u∈u，u表示用户集合；

定义候选评分物品集合给定用户u，若且使rv,i∈r成立，则称物品i为用户u的候选评分物品，用户u的候选评分物品集合为且i∈i-iu；其中，i表示物品集合，rv,i表示用户v对物品i的评分；

通过公式计算用户u对候选评分物品的预测评分

步骤5，计算用户u对物品的评分置信度。

具体的，在本发明的实施例中，上述步骤5的具体实现方式可以为：

通过公式计算用户u对物品的评分置信度。

其中，c'u,i表示用户u对候选评分物品i的评分置信度，fs(su,i)表示正向算子函数，su，i表示正向算子，表示正向算子的平均值，表示中评价过候选评分物品的用户集合，fv(vu,i)表示负向算子函数，rmax，rmin分别表示评分矩阵r中的最大评分和最小评分，vu，i表示负向算子，表示负向算子的平均值，表示用户u的平均评分，表示用户u的平均评分。

即，设用户u对候选评分物品i的预测评分为则用户u对候选评分物品i的评分置信度c'u,i定义为

其中，fs(su,i)表示正向算子函数，fv(vu,i)表示负向算子函数。评分置信度c'u,i的取值范围为(0,1)，c'u,i值越大表示预测评分越可靠。当时，评分置信度c'u,i为上式定义的方法得到，由于用户总是相信自己的，因此自己评论过的物品绝对是可靠的，可以设定cu，i＝1(i∈iu)。因此用户u对全体物品i的评分置信度可以描述为以下的公式进行计算：

其中，前文中fs(su,i)表示正向算子函数，su，i表示正向算子，表示正向算子的平均值，表示中评价过候选评分物品的用户集合，fv(vu,i)表示负向算子函数，rmax，rmin分别表示评分矩阵r中的最大评分和最小评分，vu，i表示负向算子，表示负向算子的平均值，表示用户u的平均评分，表示用户u的平均评分。

步骤6，根据所述评分置信度和填充处理后的用户物品评分矩阵，计算用户u与用户v之间的相似性。

其中，在本发明的实施例中，可使用修正的余弦相似度方法，同时在此方法的基础上加入步骤5的评分置信度共同来计算。需要说明的是，在本发明的实施例中，相似性在协同过滤过滤推荐系统中是保障质量的关键。本发明在以上隐性信任中的信任邻居对目标用户的融合评分和评分置信度因素，然后再基于皮尔逊相关系数给出相似性的计算方法。

具体的，在本发明的实施例中，上述步骤6的具体实现方式可以为：

通过公式su,v＝β×sim(u,v)'，计算用户u与用户v之间的相似性；

其中，公式中的cv，i表示用户v对物品i的评分置信度，i′uv＝i′u∩i′v表示经填充处理后的用户物品评分矩阵中用户u和用户v共同评分的物品集合，

其中β是相似度中的权重系数，n为用户共同评分物品数量，m为系统定义的共同评分数量阈值，当用户之间没有共同评分项目时，可以直接忽略相似度的影响。

需要进一步说明的是，因为sim(u,v)∈[-1,1]，为了将其值映射到[0,1]区间上，通过对进行归一化处理。这是推荐系统中常用的度量相似度的方法，但存在一定的弊端。即如果两个用户之间的共同评分项目比较少甚至完全没有的话，那么即使计算得到很高的相似度，也是不可信的。为了准确的描述相似关系，在相似度中引入了上述权重系数β。

步骤7，计算用户u的全局信任度，并计算用户u对用户v的局部信任度。

其中，在本发明的实施例中，通过基于显性信任(0-1)二值数据，计算用户的全局信任度和局部信任度。需要说明的是，全局信任度体现用户在整个信任网络中的声望、地位、可靠性等，信任网络中的每个用户都各自拥有一个全局信任值，该值由用户自己的诚信、能力等素质决定。可见，全局信任度反应的是个体在整个网络中的地位与可靠性，但无法体现出用户之间信任的差异性。而局部信任度反应的是两个用户一对一的信任关系，表现出了用户在信任网络中的个体差异性。

具体的，在本发明的实施例中，上述步骤7的具体实现方式可以为：

通过公式计算用户u的全局信任度。其中，tgl表示用户u的全局信任度，ind(u)表示用户u在信任网络中的入度，max(ind(w))为信任网络中所有节点的最大信任入度，min(ind(w))为信任网络中所有节点的最小信任入度；

通过公式计算用户u对用户v的局部信任度。其中，tlo表示用户u对用户v的局部信任度，d表示从用户u通过深度优先搜索到达用户v的最短长度，即信任传播步长，用户u到达用户v的最短路径越长，两者间的局部信任值越低，为了防止毫无意义的搜索和数据失真，限制d≤3，

其中，n(u)表示用户u的邻居集合，tuk表示信任矩阵中的用户u对用户k的信任值，tuktkv表示信任矩阵中用户k对用户v的信任值，在信任矩阵中用户u信任用户k，则tuk＝1，反之则tuk＝0。

步骤8，根据所述全局信任度和所述局部信任度，计算用户u对用户v的最终信任度。

其中，在本发明的实施例中，由于每个用户对其他用户的信任程度是不一样的，考虑到被信任者的全局信任强度不同于信任者的局部信任，为了使得信任更加准确，在引入信任传播特性来计算用户间的信任度，还要考虑全局信任和局部信任的权重分配。

具体的，在本发明的实施例中，上述步骤8的具体实现方式可以为：

通过公式tuv＝(1-α)tgl+αtlo，计算用户u对用户v的最终信任度。

其中，tuv表示用户u对用户v的最终信任度，α为局部信任所占的比重，α的取值范围为[0,1]，α的值越小，两个用户之间的信任度不是用户自身主导的，而受信任者的自身影响因素增强。α的最终的取值可以根据系统的历史数据测试得到。

步骤9，根据所述相似性和所述最终信任度，修正用户u的潜在特征用户矩阵。

其中，在本发明的实施例中，基于相似性和用户间的信任关系共同修正矩阵分解中的用户矩阵，即将信任关系与相似关系以同样的加权平均方式融入到概率矩阵分解模型中来，用信任邻居与相似邻居共同修正目标用户的特征矩阵。

具体的，在本发明的实施例中，上述步骤9的具体实现方式可以为：

通过公式修正用户u的潜在用户特征矩阵；

其中，bu和nu分别为用户u的相似邻居集和信任邻居集，wt和ws表示用户u的行为倾向权重，wt表示用户u通过信任用户来获取推荐的倾向，ws表示用户u通过评分行为获得推荐的倾向，suk表示用户u与用户k的相似度(即相似性，具体可按照用户u与用户v之间的相似性的计算方式，得到suk)，tuv表示用户u与用户v的最终信任度。

步骤10，根据所述潜在用户特征矩阵，预测用户u对物品i的评分。

其中，在本发明的实施例中，通过贝叶斯推到公示得到用户特征矩阵u和物品特征矩阵v的联合后验分布，得到最终的损失函数，通过梯度下降的方法训练参数u和v，最终通过r＝u*v计算出来用户的预测评分最后通过推荐系统的评价指标绝对平均误差(mae)和均方根误差(rmse)来计算推荐的准确性。

具体的，在本发明的实施例中，使用概率矩阵分解(pmf)的方法对信任关系和相似关系进行建模。通过pmf模型学习到用户特征矩阵u以及物品特征矩阵v，并利用公式来预测用户u对物品i的评分。

其中u是用户潜在特征矩阵，用户v是物品潜在特征矩阵。在这里用户潜在特征矩阵指修订后的用户潜在特征矩阵表示用户u的特征矩阵，vi表示项目i的潜在特征矩阵，因此用户u对物品i的预测评分为其中表示用户特征矩阵的转置矩阵。

假设在推荐系统中用户和物品的数量分别为m和n，用户集合表示为u＝{u1，u2，...um}；物品集合表示为i＝{i1，i2，...in}。给出来的用户物品评分矩阵为r＝(rui)m×n，ru,i表示用户物品评分矩阵r中用户u对物品i的评分。和分别表示的是用户和物品的潜在特征矩阵，uu和vi分别是潜在特征向量的k列向量。

pmf算法假设用户和物品的潜在特征矩阵都服从均值为0的高斯分布。

pmf算法认为用户对物品得评分是一系列概率组合问题。根据以上定义，已有评分数据得条件概率定义如公式如下：

这里，所表示的是均值为u，方差为的正态分布。iui为指示函数，如果用户u对物品i进行了评分，取值为1，否则取值为0。g(x)＝1/(1+exp(-x))是逻辑函数，用来限定预测值在范围[0,1]内。通过贝叶斯公式推导化简得到特征矩阵u与v的联合后验概率公式，即损失函数如下所示：

其中，是frobebius范数。参数λu和λv是正则化参数，用于防止过拟合。

使用梯度下降的方式来训练模型参数u和v。根据下面的公式更新模型参数u和v。对应的偏导公式如下所示：

最终的预测评分使用以下公式计算：

与现有技术相比，本发明更充分挖掘了用户的信息，缓解了评分矩阵数据稀疏的问题，以及用户冷启动的问题。在这里通过挖掘信任信息和相似性信息共同修订用户特征矩阵，而且采用该剧矩阵的方法训练模型，对于数据稀疏的效果更加能考虑到用户的偏好信息。

即，本发明通过充分挖掘稀疏的用户评分信息，构建隐性信任网络；并且对于显性的二值(0-1)信息转化为更加准确的二值信息，在这里二值信息的转化考虑到了用户的影响传播，以及局部信任和全局信任的权重的分配得到最终的信任信息。这里充分使用了用户信息和信任信息可以提高推荐的准确性。用户相似性和信任共同修订矩阵分解中的用户矩阵，并且采取全职分配的策略，对于数据稀疏有一定的缓解。使用概率矩阵分解作为最终的基础模型，可以考虑到周围邻居的影响而不单单考虑自己的影响。

在此，通过验证实验对上述协同过滤推荐方法作进一步说明。

在验证实验中，使用了网络上公开数据集filmtrust和epinions。filmtrust为guo等人从网站filmtrust完整抓取下来的公共数据集，是一个电影评分数据集，此外，该数据集还包括用户之间的信任关系，用户能够对电影做出评分，同时还可以构建单向信任关系。epinions是massa等人于从epinions评价网站上收集所得的数据集。epinions数据集中用户可以给商品评分，同时还可以给其他人的评论进行打分，标签自己信任的用户以构建有向社交网络。两个数据集的统计数据如图2所示，其中，表示每个用户平均评过分的项目数量，表示每个项目平均评过分的用户个数，表示用户的平均社交关系数。其中，项目即为前文的物品。

本方法采取的对比方法分别是pmf，rste，soreg，socialmf以及本文提出的st-pmf算法。

实验使用的方法是常用的5折交叉验证。在进行实验时，每次训练集随机选择80％的数据，最后的20％是测试数据集。在下面的实验中，依次进行5次的5折交叉实验且把五次结果的平均值作为实验的最终结果。实验中参数的具体设置如图3所示，实验中采用的推荐方法中常用的评价指标是平均绝对误差(mae)和均方根误差(rmse)。

上式中，n表示测试集中的评分数目，rij是i用户对j项目的真实评分，是i用户对j项目的预测的评分数值。本实验推荐结果的准确性就是比较真实值和预测值间的误差，mae与rmse的值越小，则说明推荐精度越高。

针对不同数据集和不同维度来对推荐的准确度进行实验，最终对于潜在特征向量维度分别设置为5和10的filmtrust数据集和epinions数据集的实验结果见图4和图5。

由图4可知：对于filmtrust的实验结果说明：pmf是最基础仅使用用户-项目评分信息的概率矩阵分解模型，其它几种模型不仅使用了用户-项目评分信息，而且使用了社交信息推荐效果较好，其中st-pmf的效果最好。说明社交信息的引入能够解决数据稀疏的问题。当维度d为5和10时，这几中使用社交信息的推荐方法的mae与rmse的值比其他几种的要小，尤其st-pmf充分挖掘了信任的深层次关系，不仅仅停留在信任表面，结合评分信息挖掘的隐性信任和衡量全局和局部的显性信任的综合考虑，考虑到信任传递，综合这些信息能对用户的行为偏好建模的模型更加好。

对于图5可知：对于epinions这样的超大规模的数据集同样可以解释。对于filmtrust和epinions数据集，当维度为5时，推荐的准确度是较高的。其中与pmf算法与基于社交网络信任的推荐方法进行比较，st-pmf的推荐准确度都是最高的，因为mae和rmse的这两个指标数据都是最小的。通过对以上两张表的分析可以说明，社交信息的引入是可以解决数据稀疏问题造成的低推荐度的问题。

以上所述是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明所述原理的前提下，还可以作出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。