一种用于航天器解体碎片不确定性参数的分布方法与流程

本发明属于航天动力学计算技术领域，更具体地说，本发明涉及一种用于航天器解体碎片不确定性参数的分布方法。

背景技术：

近地航天器受气动阻力等因素影响，其轨道高度会逐渐降低，若不进行轨道维持，则将最终再入大气层。另外，也有部分航天器，如和平号空间站等，处于种种原因考虑会主动再入大气层。在再入过程中，航天器受强气动力热影响会发生解体，产生大量碎片，其中大部分会被烧蚀，但仍有大约10％～40％的干质量会到达地面。为分析残存碎片对地面的影响，需要确定碎片参数在地面的分布。航天器再入解体后，会生成大量碎片。由于数量太大且随机因素众多，在数值模拟中逐一跟踪既不现实也不必要。可以将碎片按一定规则分为有限组，每个组拥有数量不等的同一类碎片，并在数值模拟中视为一个整体。当碎片到达地面时，会得到碎片的位置、质量、数量、能量等参数，根据算法的不同，还可以获得参数的不确定度。

技术实现要素：

本发明的一个目的是解决至少上述问题和/或缺陷，并提供至少后面将说明的优点。

为了实现根据本发明的这些目的和其它优点，提供了一种用于航天器解体碎片不确定性参数的分布方法，包括以下步骤：

步骤一、获取待处理航天器解体碎片的相关参数，包括位置、质量、数量、能量和不确定度；

步骤二、根据所有碎片的位置集合确定整个包络区域，即碎片不确定性参数的计算域，并对计算域按位置分辨率要求进行细分；

步骤三、将每一个碎片的待求参数按照一定的分布规则分布到计算域内；待求参数原本集中于一点，经过分布后，变为一个区域内的参数密度；

步骤四、对计算域内的碎片参数分布求和，得到所有碎片的不确定性参数在整个计算域内的分布。

优选的是，其中，所述碎片的参数种类须一致，其中位置参数是必须参数，通常以经纬度形式给定；碎片质量、数量和能量参数为可选的待分布参数，且质量、数量和能量参数至少应包含一个。

优选的是，其中，所述碎片参数的不确定度用(α，δ)表示，其中δ为正实数，α∈(0,1]；以获取的碎片位置为基准点，(α，δ)表示不确定性参数总量的α分布在以基准点为圆心，半径为δ的区域内。

优选的是，其中，所述步骤二中确定包络区域的具体方法为：首先根据所有碎片的位置，确定一个能包络所有碎片的最小矩形区域；再将该矩形区域向外扩展一定范围，确保后续参数分布不会超出计算域。

优选的是，其中，所述计算域的范围确定后，根据所需要的参数位置分辨率，将计算域划分为一定数量的细小矩形网格，每个细小矩形网格即为碎片参数分布的计算单元，且细小矩形网格的大小决定了最终分布的精细度。

优选的是，其中，所述分布规则为圆锥型线性分布规则，以碎片位置为中心点，以符合碎片参数不确定度的方式确定具体分布形式和系数。

优选的是，其中，所述分布规则为二维正态分布，以碎片位置为中心点，以符合碎片参数不确定度的方式确定具体分布形式和系数。

优选的是，其中，每个碎片都会对计算域一定范围内细小网格产生影响，在每一个细小网格对所有碎片求和，即得到所有碎片在整个计算域内的分布。

优选的是，其中，以碎片数量为例，所述圆锥型线性分布规则的分布步骤为：

步骤s11、获取碎片数量ni＝{λ，b，n，α，δ}，其中，λ，b表示碎片所处位置，通常分别为经度和纬度，n表示碎片数量，α和δ表示不确定度，表示参数总量的α分布在以基准点为圆心，半径为δ的区域内；

步骤s12、首先遍历所有碎片数据的位置坐标，找到λmax、λmin、bmax、bmin四个参数，由此四个参数可确定一个最小包络矩形；遍历所有碎片数据的δ参数，找到δmax，将最小包络矩形各边分别向外拓展6δmax的距离；然后对计算域按位置分辨率要求进一步细分为细小矩形网格；

步骤s13、使用圆锥型线性分布规则，将参数总量n分布在一个底面半径为l，高为h的圆锥上，并且要求以半径为δ的圆柱为界，圆柱和其上方的圆锥体积占比为α，待求系数为l和h；

根据总量一致有：圆锥体积与碎片数量相等，即v总＝ni，根据不确定度分量一致：圆柱和圆柱上方圆锥的体积之和与整个圆锥体积的比值为α，即可推得关于l和h的方程组：

αl³－3δ²l+2δ³＝0(1)

πl²h＝3ni(2)

当0＜α＜1时，由三次方程求根公式，(1)式中l的实根有且仅有一个；当α＝1时，则可以直接取l＝δ，故上述方程组可以唯一确定碎片数量不确定度的分布方式。

优选的是，其中，以数量为例，所述二维正态分布规则的分布步骤为：

步骤s21、获取碎片数量ni＝{λ，b，n，α，δ}，其中，λ，b表示碎片所处位置，通常分别为经度和纬度，n表示碎片数量，α和δ表示不确定度，表示参数总量的α分布在以基准点为圆心，半径为δ的区域内；

步骤s22、首先遍历所有碎片数据的位置坐标，找到λmax、λmin、bmax、bmin四个参数，由此四个参数可确定一个最小包络矩形；遍历所有碎片数据的δ参数，找到δmax，将最小包络矩形各边分别向外拓展6δmax的距离；然后对计算域按位置分辨率要求进一步细分为细小矩形网格；

步骤s23、碎片数量参数总量分布在全域范围内，并要求与以半径为δ的圆柱为界，其内部体积占比为α；待求系数为二维正态分布的标准差σ和中心点极值h；此处取l＝6δ；二维正态分布的概率密度函数fxy有两个标准差σx和σy，为保证定解条件，需要补充二者之间的关系式，通常取等，相关性系数ρxy一般取0；

采用二分法进行猜值计算，步骤如下：

步骤s231、设定标准差σ的猜值范围σmin，σmax，并分别计算δ范围的分布占比f(σmin)和f(σmax)；此处应保证f(σmin)＞α且f(σmax)＜α，若不满足，则需要重新设定猜值范围；

步骤s232、猜值σx＝0.5×(σmin+σmax)，并计算δ范围的分布占比f(σx)；

步骤s233、若f(σx)与α的偏差在误差允许范围内，则取σ＝σx，猜值结束，允许误差通常取10^-8～10^-6；若偏差仍较大，则继续猜值；

步骤s234、若f(σx)＞α，则设置σmin＝σx；若f(σx)＜α，则设置σmax＝σx；重复步骤s232到步骤s234，直到若f(σx)与α的偏差在误差允许范围内，取σ＝σx，猜值结束；

在获得恰当的σ之后，二维正态分布的概率密度函数fxy形式即可确定，由于概率密度函数fxy具有归一化性质，即在其的定义域内积分为1；根据总量一致原则，使其在计算域范围内对概率密度函数积分应与总量相等，即再乘以一个系数θ，使得：

求得系数θ的值，且：

θ·fxy(max)＝h(4)

由(4)式求得二维正态分布的中心点极值h，其中fxy(max)为二维正态分布概率密度函数的最大值，根据fxy的形式可以直接求得；ω为碎片的计算域，可以是步骤二中确定的全体计算域，但为了减小计算量，也可以设置为以碎片位置坐标为中心,±l所围成的矩形区域。

本发明至少包括以下有益效果：本发明通过对解体碎片参数在一定范围内的地面密度分布，便于对碎片参数数据后续相关分析，为后续的碎片参数评估提供数据支撑。同时本发明的分布方法得到的分布结果精确度高，实际操作性强。

本发明的其它优点、目标和特征将部分通过下面的说明体现，部分还将通过对本发明的研究和实践而为本领域的技术人员所理解。

附图说明：

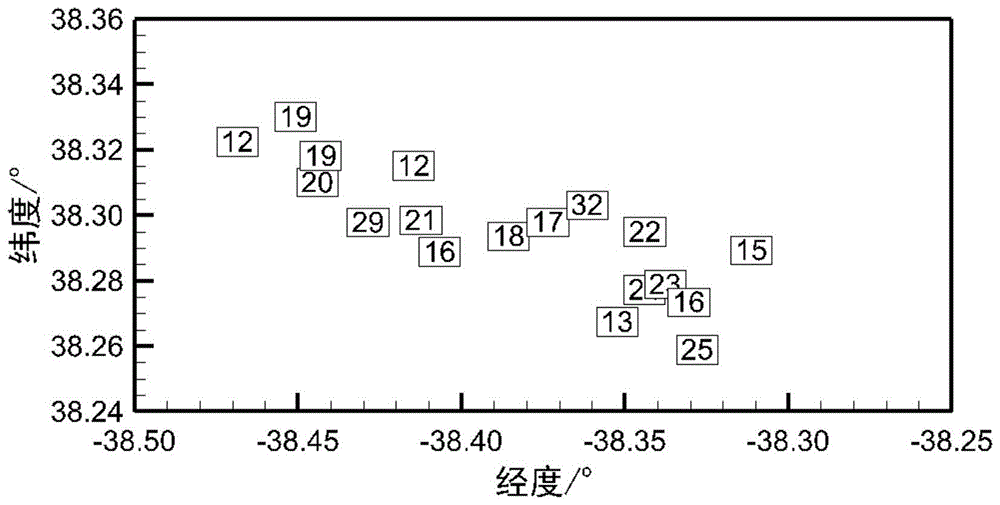
图1为待处理的航天器解体碎片参数示意图；

图2为根据已知数据确定计算域的示意图；

图3为对参数进行圆锥型线性分布的示意图；

图4为对参数进行二维正态分布的3d示意图；

图5为对参数进行二维正态分布的2d示意图；

图6为图1中碎片参数进行圆锥型线性分布的结果；

图7为图1中碎片参数进行二维正态分布的结果。

具体实施方式：

下面结合附图对本发明做进一步的详细说明，以令本领域技术人员参照说明书文字能够据以实施。

应当理解，本文所使用的诸如“具有”、“包含”以及“包括”术语并不配出一个或多个其它元件或其组合的存在或添加。

实施例1：

步骤一、获取碎片数量ni＝{λ，b，n，α，δ}，其中，λ，b表示碎片所处位置，通常分别为经度和纬度，n表示碎片数量，α和δ表示不确定度，表示参数总量的α分布在以基准点为圆心，半径为δ的区域内；如图1所示，图中数值表示在该位置的碎片数量，共获取18组数据，即ni(i＝1，2，…，18)，图中小方块的坐标表示已知的碎片位置，小方块内的数值表示在该位置的碎片数量，并已知α和δ。可以看出原始数据为点状的集中式数据；

步骤二、首先遍历所有碎片数据的位置坐标，找到λmax、λmin、bmax、bmin四个参数，由此四个参数可确定一个最小包络矩形，如图2所示；遍历所有碎片数据的δ参数，找到δmax，将最小包络矩形各边分别向外拓展6δmax的距离；然后对计算域按位置分辨率要求进一步细分为细小矩形网格，例如本例中可以将虚线矩形划分为nlength×nwide个小矩形，其中nlength和nwide可以直接给定，也可以根据计算域范围和要求精度计算得出；

步骤三、使用圆锥型线性分布规则，将参数总量n分布在一个底面半径为l，高为h的圆锥上，并且要求以半径为δ的圆柱为界，其内部体积占比为α，待求系数为l和h；

根据总量一致有：圆锥体积与碎片数量相等，即v总＝ni，根据不确定度分量一致：圆柱和圆柱上方圆锥的体积之和与整个圆锥体积的比值为α，即可推得关于l和h的方程组：

αl³－3δ²l+2δ³＝0(1)

πl²h＝3ni(2)

当0＜α＜1时，由三次方程求根公式，(1)式中l的实根有且仅有一个；当α＝1时，则可以直接取l＝δ，故上述方程组可以唯一确定碎片数量不确定度的分布方式。

步骤四、通过步骤三得到每组参数的分布形式后，即可以求得计算域内任一位置的该组参数密度；遍历步骤二确定的每一个矩形小网格，并对全部碎片参数求和，即得到计算域内的碎片数量参数密度分布；对于图1所示的示例数据，经圆锥型线性分布的最终结果如图6所示，求得的碎片数量密度最大值为22个/km²。

实施例2：

步骤一、获取碎片数量ni＝{λ，b，n，α，δ}，其中，λ，b表示碎片所处位置，通常分别为经度和纬度，n表示碎片数量，α和δ表示不确定度，表示参数总量的α分布在以基准点为圆心，半径为δ的区域内；如图1所示，图中数值表示在该位置的碎片数量，共获取18组数据，即ni(i＝1，2，…，18)，图中小方块的坐标表示已知的碎片位置，小方块内的数值表示在该位置的碎片数量，并已知α和δ。可以看出原始数据为点状的集中式数据；

步骤二、首先遍历所有碎片数据的位置坐标，找到λmax、λmin、bmax、bmin四个参数，由此四个参数可确定一个最小包络矩形，如图2所示；遍历所有碎片数据的δ参数，找到δmax，将最小包络矩形各边分别向外拓展6δmax的距离；然后对计算域按位置分辨率要求进一步细分为细小矩形网格，例如本例中可以将虚线矩形划分为nlength×nwide个小矩形，其中nlength和nwide可以直接给定，也可以根据计算域范围和要求精度计算得出；

步骤三、如图4、图5所示，图4中粗实线为分界线，对应于图5中半径为δ的圆柱，图5为图4的一个平行于坐标轴且过中心点的剖面图，便于标记和阐述；碎片数量参数总量分布在全域范围内，并要求与以半径为δ的圆柱为界，其内部体积占比为α；待求系数为二维正态分布的标准差σ和中心点极值h；理论上二维正态分布的参数总量可以分布在全域范围内，但是从正态分布特性可知：3σ范围内即可覆盖99％以上的分布。由于标准差属于未知参数，为保险起见，此处取l＝6δ；二维正态分布的概率密度函数fxy有两个标准差σx和σy，为保证定解条件，需要补充二者之间的关系式，通常取等，相关性系数ρxy一般取0；

采用二分法进行猜值计算，步骤如下：

步骤s231、设定标准差σ的猜值范围σmin，σmax，并分别计算δ范围的分布占比f(σmin)和f(σmax)；此处应保证f(σmin)＞α且f(σmax)＜α，若不满足，则需要重新设定猜值范围；

步骤s232、猜值σx＝0.5×(σmin+σmax)，并计算δ范围的分布占比f(σx)；

步骤s233、若f(σx)与α的偏差在误差允许范围内，则取σ＝σx，猜值结束，允许误差通常取10^-8～10^-6；若偏差仍较大，则继续猜值；

步骤s234、若f(σx)＞α，则设置σmin＝σx；若f(σx)＜α，则设置σmax＝σx；重复步骤s232到步骤s234，直到若f(σx)与α的偏差在误差允许范围内，取σ＝σx，猜值结束；

在获得恰当的σ之后，二维正态分布的概率密度函数fxy形式即可确定，由于概率密度函数fxy具有归一化性质，即在其的定义域内积分为1；根据总量一致原则，使其在计算域范围内对概率密度函数积分应与总量相等，即再乘以一个系数θ，使得：

求得系数θ的值，且：

θ·fxy(max)＝h(4)

由(4)式求得二维正态分布的中心点极值h，其中fxy(max)为二维正态分布概率密度函数的最大值，根据fxy的形式可以直接求得；ω为碎片的计算域，可以是步骤二中确定的全体计算域，但为了减小计算量，也可以设置为以碎片位置坐标为中心,±l所围成的矩形区域。

步骤四、通过步骤三得到每组参数的分布形式后，即可以求得计算域内任一位置的该组参数密度；遍历步骤二确定的每一个矩形小网格，并对全部碎片参数求和，即得到计算域内的碎片数量参数密度分布；对于图1所示的示例数据，经二维正态分布的最终结果如图7所示，求得的碎片数量密度最大值为24个/km²。

这里说明的设备数量和处理规模是用来简化本发明的说明的。对本发明的应用、修改和变化对本领域的技术人员来说是显而易见的。

尽管本发明的实施方案已公开如上，但其并不仅仅限于说明书和实施方式中所列运用，它完全可以被适用于各种适合本发明的领域，对于熟悉本领域的人员而言，可容易地实现另外的修改，因此在不背离权利要求及等同范围所限定的一般概念下，本发明并不限于特定的细节和这里示出与描述的图例。