一种电力现货市场的综合评价方法与流程

本发明涉及电力市场的
技术领域：
，更具体地，涉及一种电力现货市场的综合评价方法。
背景技术：
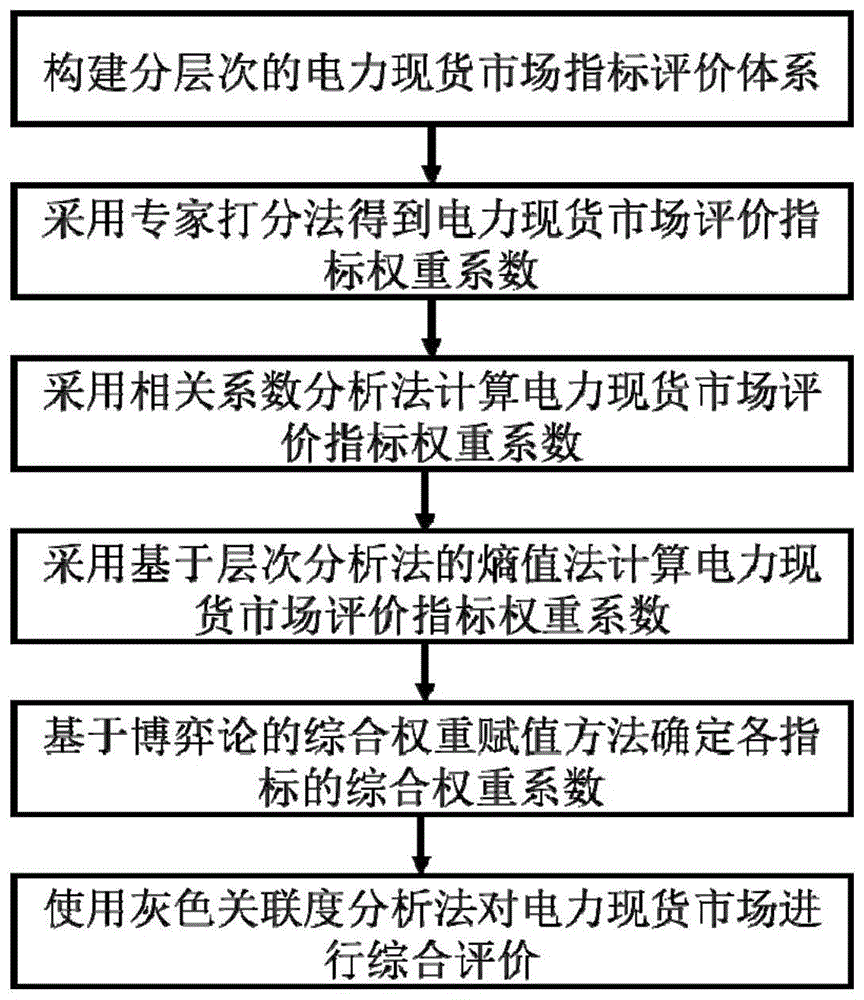
：电力现货市场是指将电能作为一种商品进行实时交易或准实时交易的交易市场，其建设目的是为了在电力行业中引入市场竞争，利用市场化所带来的市场竞争引导电力现货市场整体的社会资源的优化配置，获得更大的社会效益。国外于上世纪90年代开始开展电力市场改革。电力市场改革最先在西欧开展，随后被推广到了美国以及大洋洲的一些电力公司。截止至2009年，全球人口的86.49％经历了电力市场化改革，电力市场化改革的国家gdp综合占据全球gdp的94％。目前，世界上成熟的电力交易市场主要有美国的pjm电力现货市场、北欧电力市场、英国电力市场以及澳大利亚电力市场等电力市场。我国于2002年开始进行电力市场化改革，如今已过去17年，取得了一定的成果。目前，南方(广东以起步)电力现货市场作为全国选定的八个现货试点区域已经建立起区域性质的电力现货市场，并于2019年5月15日与16日进行我国首次电力现货交易结算，开始推进实时市场的建设。另外，浙江也即将开始进行电力现货市场的试运行。然而我国当前对于电力市场的建设仍处于初步探索的阶段，而且尚未建立起一套行之有效的电力市场评价指标体系。在新的市场竞争下，电力市场信息瞬息万变，市场的不良运作或者市场危机的出现都将对地区甚至整个电力行业产生严重的破坏。所以，无论是市场中的发电方还是购电方，市场运营者还是市场监管者，都十分关注市场的运营情况，都有分析评估市场健康程度的需求。因此，电力现货市场评价体系的构建及其综合评价方法的确定都是目前我国电力市场改革的一个重要方向，也是下一阶段电力市场建设的重点讨论对象。技术实现要素：本发明主要构建了基于集中式市场的电力现货市场评价体系，并提出了基于综合权重系数的灰色关联度分析的多属性综合评价方法。本发明采用以下技术方案实现：一种电力现货市场的综合评价方法，包括以下步骤：s1：从电力市场的经济学特性和电力系统的物理特性出发，选取分层次的指标体系作为评价体系基本框架；s2：采用专家打分法得到电力现货市场评价指标权重系数；s3：采用相关系数分析法计算电力现货市场评价指标权重系数；s4：采用基于层次分析法的熵值法计算电力现货市场评价指标权重系数；s5：利用基于博弈论的综合权重赋值方法，结合多种赋权方法的优点，确定各指标的综合权重系数；s6：结合电力现货市场具有灰色性特点，使用灰色关联度分析法对市场进行综合评价。上述技术方案中，进一步地，s1从电力市场的经济学特性和电力系统的物理特性出发，选取分层次的指标体系作为评价体系基本框架，具体实现方法如下：遵循全面性、简洁性、可行性、可比性、引导性、重点性的原则建立分层次的电力现货市场评价指标体系。以市场安全水平、市场运营水平、市场效益水平以及市场调度水平四个方面作为市场的主要运行状态指标进行评估，展开构建起完整科学的包括系统层、状态层、结构层、指标层的四级电力现货市场评价系统，在一些指标中再次向下展开次级指标层，例如电压波动指标中再次向下展开为电压正波动率、电压负波动率、电压波动影响时间占比三个次级指标。所构建的电力现货市场评价体系结合我国国情在建设性提出购电商侧市场局部结构指标、市场保障信息安全水平、市场结算类指标等指标。表4所示为电力现货市场评价指标体系的整体框架。表4电力现货市场评价指标体系整体框架更进一步地，s2采用专家打分法得到电力现货市场评价指标权重系数，具体实现方法如下：专家打分法又称德尔菲法，是主观赋权法中最简单明了的一种方法。它主要通过若干对评估对象有着很高的熟悉度的专家，借助其经验、知识以及个人偏好对评价体系中的指标权重进行打分，并借助统计方法对打分的结果进行适当处理，得到最终的权重系数。其具体评价模型如下：(1)根据专家对每个指标的打分意见构建初步指标权重矩阵式中：xi表示第i个专家对于指标权重的赋值方案；ωij表示第i个专家对于第j个指标权重的赋值。(2)计算每个指标的权重系数平均值式中：表示第j个指标权重系数的平均值。(3)计算每个指标的权重系数与平均值的差异水平式中：δωij表示第i个专家对于第j个指标权重的赋值与所有专家对于第j个指标权重赋值的平均值之间的差异。(4)对于差异δωj比较大的第j个指标需要再次邀请若干专家对其进行重新评估，赋予权重系数，反复上述(1)-(3)步骤，直至评价体系中每一个指标所有专家对其的评价以及权重系数的赋值在一定的偏差内，并将最后一次得到的初步指标权重矩阵记录下来：利用该矩阵求取每一个指标的平均权重赋值并作为最终的指标权重，即式中：p1表示采用第一类赋权方法即专家赋权法得到的权重系数向量。s3采用相关系数分析法计算电力现货市场评价指标权重系数，具体实现方法如下：在实际的指标体系构建中，无法避免地会提出一些指标存在某些指标功能上的重复或者相似，而如果采用类似于专家打分法等方法则会使得这方面的指标的权重被放大或者缩小，导致最后的评估结果并不理想。相关系数分析法则是通过比较指标之间的相关系数来判断指标之前的内在相关性。相关性越大，各指标之间信息的覆盖率与重复率越高，相应的权重赋值则越小；反之，相关性越小，各指标之间信息的覆盖率与重复率越低，相应的权重赋值则越大。在统计学中，皮尔逊相关系数一般用于两个变量之间的相关性量化表示，因此，在这里采用皮尔逊相关系数来表征指标之间的相关性。式中：ρ(p,q)表示指标p与指标q之间的相关系数；xip，xiq表示第i个电力现货市场中第p个和第q个指标数值；和表示电力现货市场中第p个和第q个指标的平均值。当指标数值中存在一组或一组以上指标为恒定值时，将会导致在计算相关系数时分母为0，计算出错。这里对数据进行0.1％的微小扰动，同时保证指标数值之和不变，这样就能解决分母为零而无法计算的问题。可以写出相关系数矩阵：从而可以确定每个指标的权重系数为：式中：ωj表示第j个指标的权重系数。将指标权重以权重向量的形式表示为：p2＝[ω1,ω2,l,ωi,l,ωn](i＝1,2,l,n)(44)式中：p2表示采用第二类赋权方法即相关系数分析法得到的权重系数向量。s4采用基于层次分析法的熵值法计算电力现货市场评价指标权重系数，具体实现方法如下：组合赋权法是基于最优化理论而提出的，具有涵盖主客观赋权的特点，能够避免人为因素和样本差异对指标重要程度的过度影响。在这里采用一种基于层次分析法的熵值法来进行对指标的组合赋权。层次分析法是一种主观赋权法，具有定性与定量相结合处理各种决策因素的特点。其基本思路是确定判断矩阵，两两比较判断矩阵中各元素之间的相对重要性，然后对评价指标进行赋值；熵值法则是一种客观赋权法，利用信息熵来进行指标权重的赋值。在信息论中，熵是对不确定性的一种度量，也可以用来判断某个指标的离散程度。在评价体系中，当一个指标在不同的电力现货市场中离散程度越小，熵越大，表示其不确定性越小，其所携带的反应不同电力现货市场差异的信息也就越小，在进行市场之间比较时所起到的作用越小，权重系数也就越小；反之，熵越小，权重系数越大。基于层次分析法的熵值法的主要思路是在每一层次的分析中，分别用传统的层次分析法与熵值法进行权重系数的赋值，并将两者相乘得到该方面的组合权重赋值。该处理方法既能体现出人为因素上影响，能够通过市场评价来体现出政策上的变化对市场发展趋势具有指导意义；另一方面，熵值法则是能够将不同市场之间的差异性放大体现在评价结果中，方便不同市场之间的比较与完善。步骤1：利用传统的层次分析法对电力现货市场评价体系中的各个指标进行权重赋值得到(1)根据前文中以建立的电力现货市场评价体系构建层次结构模型；(2)构建判断矩阵xahp根据表5中列出的比例标度表对指标之间进行两两对比，并将结果写作判断矩阵xahp。表5层次分析法比例标度表因素a与因素b的关系量化值同等重要1稍微重要3较强重要5强烈重要7极端重要9两相邻判断的中间值2,4,6,8式中：表示第i个指标与第j个指标之间的重要程度判定结果。同时，判断矩阵xahp还具有以下两个特点：(3)求取判断矩阵xahp的最大特征根以及对应的归一化处理后的特征向量中的元素是同一层次下对更高层次标准和规则的相对重要性的排序权值，故该过程也被称为层次单排序。(4)一致性检验。并非所有的判断矩阵都能进行层次单排序，当判断矩阵确定不一致性偏差较大时，无法进行层次单排序。故在此需要进行一致性检验，对判断矩阵的确定不一致进行检验。式中：表示判断矩阵的第i个特征值；cii表示判断矩阵第i个特征值的一致性指标，当cii＝0时，有完全的一致性，当cii接近于0时，有满意的一致性，当cii越大时，不一致性越大；ri表示判断矩阵的平均随机一致性指标，一般使用表6所示的平均随机一致性指标ri标准值进行判断；cimax表示对于最大特征根所得到一致性指标；cr表示判断矩阵的检验系数，一般，如果cr＜0.1，则认为该判断矩阵通过一致性检验。表6平均随机一致性指标ri标准值(5)一致性的改进。若判断矩阵没有通过一致性检验时，需要重新征求专家意见重新计算。但是这样会大大增加专家可能的工作量，这里使用一种一致性改进方法对判断矩阵的元素进行调整，使其一致性在一定程度上降低。一致性改进的步骤如下：1)对判断矩阵xahp进行列归一化：其中式中：xahp*表示列归一化后的判断矩阵；表示列归一化后的判断矩阵内的元素。2)利用“和积法”求排序向量：其中3)插入诱导矩阵其中4)找到诱导矩阵中最大值元素所在位置(i,j)，并将原始判断矩阵中相应位置的元素修正为同时将修正为5)重新进行一致性检验，若仍不满足一致性检验则重复1)至4)直至满足一致性检验。6)层次排序以及一致性检验。在每个层次中，根据其所有因素对于更高一层的相对重要性的权值进行排序，直到排序至最高层即目标层，同时进行一致性检验。步骤2：利用熵值法根据电力现货市场运行数据对各个指标进行权重赋值得到(1)对每一个指标数据进行标准化处理，根据公式处理即可得到结果，并将每一组指标数据表示为如下的电力市场运行效果指标矩阵式中：mi表示第i个电力市场运行效果指标向量；xij表示第i个电力市场中第j个指标。(2)计算每个指标下每个电力市场所占比重式中：pij表示第i个电力市场中第j个指标在第j个指标中的比重。(3)计算每个指标的熵值其中式中：ej表示第j个指标的熵值；k为修正系数。(4)计算每个指标的权重系数式中：pj表示第j个指标的权重系数。步骤3：将传统的层次分析法得到的权重系数与熵值法计算得到的权重系数相乘得到组合系数即：步骤4：若有更高级别的评价层次，则再次重复上述步骤。步骤5：将所有指标的权重赋值按照前文的赋值进行所占比重进行重新计算，即：式中：表示最终的指标权重系数，得到最终的电力现货市场评价体系中指标的权重系数向量p3，表示为：式中：p3表示采用第三类赋权方法即基于层次分析法的熵值法得到的权重系数向量。s5利用基于博弈论的综合权重赋值方法，结合多种赋权方法的优点，确定各指标的综合权重系数，具体实现方法如下：步骤1：计算目标权重向量ωres:式中：ωi表示k种权重系数确定方法下第i中方法下得到的权重向量；αi为线性组合系数，表示第i中方法下得到的权重向量在目标权重向量中的影响程度。步骤2：将目标权重向量集化表示为向量集步骤3：求取最优αi使得目标权重向量集与各个权重向量之间的偏差最小，即：根据其微分性质可得其最优化一阶导数条件为：步骤4：根据求解的最优αi表示出最终的综合权重向量ωop。s6：结合电力现货市场具有灰色性特点，使用灰色关联度分析法对市场进行综合评价，具体实现方法如下：根据权重系数产生的原因，在这里将上述三种权重系数进行如下定义：(1)基本权重系数基本权重系数指的是利用专家打分法得到权重系数。由于其是根据专家的知识以及经验得到的结果，一定程度上反应了学术界以及工程届对于该问题的专业看法，具有十分重要参考意义，可以作为权重系数的基本赋值。(2)可能权重系数可能权重系数指的是利用客观赋权法得到的权重系数。由于客观赋权法是根据数据之间的差异性对指标进行赋值，即在具体应用时，它为决策者指明了具体算例中需要重点进行关注的指标。故称之为可能权重系数。(3)参考权重系数参考权重系数指的是利用组合权重赋值法得到的结果。该种方法简单考虑了主客观赋值法的优缺点，具有一定的最优化性，可以作为一些较为简单的指标体系的最终权重系数，故称之为参考权重系数。但是，当其应用于像电力现货市场评价体系如此庞大复杂的评价体系时，显得较为的简单单薄，可信度不够高。可以看到，在前文中利用不同方法得到的权重系数之间存在不一致关系，为了能够对各个方法之间的权重进行协调，得到一个均衡结果，使得权重系数更加科学全面客观，能够应用于复杂庞大的评价体系中，本文采用基于博弈论的组合权重确定方法。该方法根据博弈论的原理，通过对不同的权重系数进行集化，协调不同方法之间的不一致性，得到最终的比较合理的权重系数赋值。集权模型一般可分为以下三种：博弈集结模型、团队集结模型以及群体集结模型。基于博弈论的组合权重确定方法采用博弈集结模型，基本思路是在不同的权重系数向量中寻找到一种组合权重系数向量，使得该向量与其他向量之间的距离之和为最小值，即综合权重与各种方法得到的权重之间的偏差最小，其实质是一个多人优化问题。步骤1：对每一个指标数据进行标准化处理，根据公式处理即可得到结果，并将每一组指标数据表示为如下的电力市场运行效果评价矩阵式中：ma0表示理论运行状态下电力市场运行效果评价向量，st0j表示理论运行状态下第j列指标的值，一般默认为1，mai表示第i个电力市场运行效果评价向量，stij表示第i个电力市场中第j列指标的值。步骤2：电力市场运行效果评价矩阵乘上由博弈集结模型得到的综合指标权重系数得到电力市场综合运行效果评价矩阵，即式中：cma0表示理论运行状态下电力市场综合运行效果评价向量，cst0j表示理论运行状态下第j列指标综合评价值，cmai表示第i个电力市场综合运行效果评价向量，cstij表示第i个电力市场中第j列指标综合评价值，ωj表示第j个指标的综合权重系数。步骤3：求取电力市场运行效果评价矩阵差数列矩阵其中δcstij＝|cst0j-cstij|(i＝1,2,l,m；j＝1,2,l,n)(68)式中：δcmai表示第i个电力市场综合运行效果评价向量与理论运行状态下运行效果评价向量的差异向量。步骤4：求取每个市场下每个指标与理论运行状态下相应指标的灰色关联系数式中，δm为电力市场运行效果评价矩阵差数列矩阵中最小的值即δm为电力市场运行效果评价矩阵差数列矩阵中最大的值即ρ为分辨系数，取值范围为[0,1]，影响灰色关联系数ξij的整体水平上的数值大小，但是对最终的关联系数排序没有影响，一般取经验值0.618。步骤5：求取每个市场与理论运行状态下市场的关联度步骤6：将得到的关联度γi进行从大到小顺序的排序，得到关于i个电力市场运行情况从优到劣的排序，并得到一个相对评分值即关联度的数值γi。本发明提供的技术方案的有益效果：为了使得权重系数更加科学合理，本发明利用基于博弈论的综合权重系数确定方法对主客观赋权法以及组合赋权法所得到的三组权重系数进行权重系数的重新获取。在该方法中，主观赋值法带来人为加大某一指标的权重以反映政策上的导向的功能，客观赋值法带来筛选数据找到差异性最大的数据进行比较的功能，组合赋值法带来具有一定科学合理性的权重系数以作为参考。因此，本发明所提出的综合权重赋值方法相较于其他的单一赋值方法或简单组合赋值方法具有较大优势。在此基础上本发明采用了适用于灰色系统的灰色关联度分析方法进行电力现货市场的综合评价。该方法主要使用已有数据与理论最佳状态的数据进行相似或相异程度的比较，从而得到电力现货市场之间相对的优劣判断，有利于市场管理者了解市场的运行状态并对存在的问题进行分析和解决。附图说明图1是本发明的整体流程示意图。图2是本发明的指标体系基本框架。图3是本发明的中长期交易部分所有权重系数确定方法下指标权重对比。具体实施方式附图仅用于示例性说明，不能理解为对本专利的限制；对于本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。附图中描述位置关系仅用于示例性说明，不能理解为对本专利的限制。本发明的一种电力现货市场的综合评价方法，其实现流程包括以下步骤：s1从电力市场的经济学特性和电力系统的物理特性出发，选取分层次的指标体系作为评价体系基本框架，具体实现方法如下：遵循全面性、简洁性、可行性、可比性、引导性、重点性的原则建立分层次的电力现货市场评价指标体系。以市场安全水平、市场运营水平、市场效益水平以及市场调度水平四个方面作为市场的主要运行状态指标进行评估，展开构建起完整科学的包括系统层、状态层、结构层、指标层的四级电力现货市场评价系统，在一些指标中再次向下展开次级指标层，例如电压波动指标中再次向下展开为电压正波动率、电压负波动率、电压波动影响时间占比三个次级指标。所构建的电力现货市场评价体系结合我国国情在建设性提出购电商侧市场局部结构指标、市场保障信息安全水平、市场结算类指标等指标。表7所示为电力现货市场评价指标体系的整体框架。表7电力现货市场评价指标体系整体框架s2采用专家打分法得到电力现货市场评价指标权重系数，具体实现方法如下：专家打分法又称德尔菲法，是主观赋权法中最简单明了的一种方法。它主要通过若干对评估对象有着很高的熟悉度的专家，借助其经验、知识以及个人偏好对评价体系中的指标权重进行打分，并借助统计方法对打分的结果进行适当处理，得到最终的权重系数。其具体评价模型如下：(1)根据专家对每个指标的打分意见构建初步指标权重矩阵式中：xi表示第i个专家对于指标权重的赋值方案；ωij表示第i个专家对于第j个指标权重的赋值。(2)计算每个指标的权重系数平均值式中：表示第j个指标权重系数的平均值。(3)计算每个指标的权重系数与平均值的差异水平式中：δωij表示第i个专家对于第j个指标权重的赋值与所有专家对于第j个指标权重赋值的平均值之间的差异。(4)对于差异δωj比较大的第j个指标需要再次邀请若干专家对其进行重新评估，赋予权重系数，反复上述(1)-(3)步骤，直至评价体系中每一个指标所有专家对其的评价以及权重系数的赋值在一定的偏差内，并将最后一次得到的初步指标权重矩阵记录下来：利用该矩阵求取每一个指标的平均权重赋值并作为最终的指标权重，即式中：p1表示采用第一类赋权方法即专家赋权法得到的权重系数向量。s3采用相关系数分析法计算电力现货市场评价指标权重系数，具体实现方法如下：在实际的指标体系构建中，无法避免地会提出一些指标存在某些指标功能上的重复或者相似，而如果采用类似于专家打分法等方法则会使得这方面的指标的权重被放大或者缩小，导致最后的评估结果并不理想。相关系数分析法则是通过比较指标之间的相关系数来判断指标之前的内在相关性。相关性越大，各指标之间信息的覆盖率与重复率越高，相应的权重赋值则越小；反之，相关性越小，各指标之间信息的覆盖率与重复率越低，相应的权重赋值则越大。在统计学中，皮尔逊相关系数一般用于两个变量之间的相关性量化表示，因此，在这里采用皮尔逊相关系数来表征指标之间的相关性。式中：ρ(p,q)表示指标p与指标q之间的相关系数；xip，xiq表示第i个电力现货市场中第p个和第q个指标数值；和表示电力现货市场中第p个和第q个指标的平均值。当指标数值中存在一组或一组以上指标为恒定值时，将会导致在计算相关系数时分母为0，计算出错。这里对数据进行0.1％的微小扰动，同时保证指标数值之和不变，这样就能解决分母为零而无法计算的问题。可以写出相关系数矩阵：从而可以确定每个指标的权重系数为：式中：ωj表示第j个指标的权重系数。将指标权重以权重向量的形式表示为：p2＝[ω1,ω2,l,ωi,l,ωn](i＝1,2,l,n)(79)式中：p2表示采用第二类赋权方法即相关系数分析法得到的权重系数向量。s4采用基于层次分析法的熵值法计算电力现货市场评价指标权重系数，具体实现方法如下：组合赋权法是基于最优化理论而提出的，具有涵盖主客观赋权的特点，能够避免人为因素和样本差异对指标重要程度的过度影响。在这里采用一种基于层次分析法的熵值法来进行对指标的组合赋权。层次分析法是一种主观赋权法，具有定性与定量相结合处理各种决策因素的特点。其基本思路是确定判断矩阵，两两比较判断矩阵中各元素之间的相对重要性，然后对评价指标进行赋值；熵值法则是一种客观赋权法，利用信息熵来进行指标权重的赋值。在信息论中，熵是对不确定性的一种度量，也可以用来判断某个指标的离散程度。在评价体系中，当一个指标在不同的电力现货市场中离散程度越小，熵越大，表示其不确定性越小，其所携带的反应不同电力现货市场差异的信息也就越小，在进行市场之间比较时所起到的作用越小，权重系数也就越小；反之，熵越小，权重系数越大。基于层次分析法的熵值法的主要思路是在每一层次的分析中，分别用传统的层次分析法与熵值法进行权重系数的赋值，并将两者相乘得到该方面的组合权重赋值。该处理方法既能体现出人为因素上影响，能够通过市场评价来体现出政策上的变化对市场发展趋势具有指导意义；另一方面，熵值法则是能够将不同市场之间的差异性放大体现在评价结果中，方便不同市场之间的比较与完善。步骤1：利用传统的层次分析法对电力现货市场评价体系中的各个指标进行权重赋值得到(1)根据前文中以建立的电力现货市场评价体系构建层次结构模型；(2)构建判断矩阵xahp根据表8中列出的比例标度表对指标之间进行两两对比，并将结果写作判断矩阵xahp。表8层次分析法比例标度表因素a与因素b的关系量化值同等重要1稍微重要3较强重要5强烈重要7极端重要9两相邻判断的中间值2,4,6,8式中：表示第i个指标与第j个指标之间的重要程度判定结果。同时，判断矩阵xahp还具有以下两个特点：(3)求取判断矩阵xahp的最大特征根以及对应的归一化处理后的特征向量中的元素是同一层次下对更高层次标准和规则的相对重要性的排序权值，故该过程也被称为层次单排序。(4)一致性检验。并非所有的判断矩阵都能进行层次单排序，当判断矩阵确定不一致性偏差较大时，无法进行层次单排序。故在此需要进行一致性检验，对判断矩阵的确定不一致进行检验。式中：表示判断矩阵的第i个特征值；cii表示判断矩阵第i个特征值的一致性指标，当cii＝0时，有完全的一致性，当cii接近于0时，有满意的一致性，当cii越大时，不一致性越大；ri表示判断矩阵的平均随机一致性指标，一般使用表9所示的平均随机一致性指标ri标准值进行判断；cimax表示对于最大特征根所得到一致性指标；cr表示判断矩阵的检验系数，一般，如果cr＜0.1，则认为该判断矩阵通过一致性检验。表9平均随机一致性指标ri标准值(5)一致性的改进。若判断矩阵没有通过一致性检验时，需要重新征求专家意见重新计算。但是这样会大大增加专家可能的工作量，这里使用一种一致性改进方法对判断矩阵的元素进行调整，使其一致性在一定程度上降低。一致性改进的步骤如下：1)对判断矩阵xahp进行列归一化：其中式中：xahp*表示列归一化后的判断矩阵；表示列归一化后的判断矩阵内的元素。2)利用“和积法”求排序向量：其中3)插入诱导矩阵其中4)找到诱导矩阵中最大值元素所在位置(i,j)，并将原始判断矩阵中相应位置的元素修正为同时将修正为5)重新进行一致性检验，若仍不满足一致性检验则重复1)至4)直至满足一致性检验。6)层次排序以及一致性检验。在每个层次中，根据其所有因素对于更高一层的相对重要性的权值进行排序，直到排序至最高层即目标层，同时进行一致性检验。步骤2：利用熵值法根据电力现货市场运行数据对各个指标进行权重赋值得到(1)对每一个指标数据进行标准化处理，根据公式处理即可得到结果，并将每一组指标数据表示为如下的电力市场运行效果指标矩阵式中：mi表示第i个电力市场运行效果指标向量；xij表示第i个电力市场中第j个指标。(2)计算每个指标下每个电力市场所占比重式中：pij表示第i个电力市场中第j个指标在第j个指标中的比重。(3)计算每个指标的熵值其中式中：ej表示第j个指标的熵值；k为修正系数。(4)计算每个指标的权重系数式中：pj表示第j个指标的权重系数。步骤3：将传统的层次分析法得到的权重系数与熵值法计算得到的权重系数相乘得到组合系数即：步骤4：若有更高级别的评价层次，则再次重复上述步骤。步骤5：将所有指标的权重赋值按照前文的赋值进行所占比重进行重新计算，即：式中：表示最终的指标权重系数，得到最终的电力现货市场评价体系中指标的权重系数向量p3，表示为：式中：p3表示采用第三类赋权方法即基于层次分析法的熵值法得到的权重系数向量。s5：利用基于博弈论的综合权重赋值方法，结合多种赋权方法的优点，确定各指标的综合权重系数，具体实现方法如下：步骤1：计算目标权重向量ωres:式中：ωi表示k种权重系数确定方法下第i中方法下得到的权重向量；αi为线性组合系数，表示第i中方法下得到的权重向量在目标权重向量中的影响程度。步骤2：将目标权重向量集化表示为向量集步骤3：求取最优αi使得目标权重向量集与各个权重向量之间的偏差最小，即：根据其微分性质可得其最优化一阶导数条件为：步骤4：根据求解的最优αi表示出最终的综合权重向量ωop。s6：结合电力现货市场具有灰色性特点，使用灰色关联度分析法对市场进行综合评价，具体实现方法如下：根据权重系数产生的原因，在这里将上述三种权重系数进行如下定义：(1)基本权重系数基本权重系数指的是利用专家打分法得到权重系数。由于其是根据专家的知识以及经验得到的结果，一定程度上反应了学术界以及工程届对于该问题的专业看法，具有十分重要参考意义，可以作为权重系数的基本赋值。(2)可能权重系数可能权重系数指的是利用客观赋权法得到的权重系数。由于客观赋权法是根据数据之间的差异性对指标进行赋值，即在具体应用时，它为决策者指明了具体算例中需要重点进行关注的指标。故称之为可能权重系数。(3)参考权重系数参考权重系数指的是利用组合权重赋值法得到的结果。该种方法简单考虑了主客观赋值法的优缺点，具有一定的最优化性，可以作为一些较为简单的指标体系的最终权重系数，故称之为参考权重系数。但是，当其应用于像电力现货市场评价体系如此庞大复杂的评价体系时，显得较为的简单单薄，可信度不够高。可以看到，在前文中利用不同方法得到的权重系数之间存在不一致关系，为了能够对各个方法之间的权重进行协调，得到一个均衡结果，使得权重系数更加科学全面客观，能够应用于复杂庞大的评价体系中，本文采用基于博弈论的组合权重确定方法。该方法根据博弈论的原理，通过对不同的权重系数进行集化，协调不同方法之间的不一致性，得到最终的比较合理的权重系数赋值。集权模型一般可分为以下三种：博弈集结模型、团队集结模型以及群体集结模型。基于博弈论的组合权重确定方法采用博弈集结模型，基本思路是在不同的权重系数向量中寻找到一种组合权重系数向量，使得该向量与其他向量之间的距离之和为最小值，即综合权重与各种方法得到的权重之间的偏差最小，其实质是一个多人优化问题。步骤1：对每一个指标数据进行标准化处理，根据公式处理即可得到结果，并将每一组指标数据表示为如下的电力市场运行效果评价矩阵式中：ma0表示理论运行状态下电力市场运行效果评价向量，st0j表示理论运行状态下第j列指标的值，一般默认为1，mai表示第i个电力市场运行效果评价向量，stij表示第i个电力市场中第j列指标的值。步骤2：电力市场运行效果评价矩阵乘上由博弈集结模型得到的综合指标权重系数得到电力市场综合运行效果评价矩阵，即式中：cma0表示理论运行状态下电力市场综合运行效果评价向量，cst0j表示理论运行状态下第j列指标综合评价值，cmai表示第i个电力市场综合运行效果评价向量，cstij表示第i个电力市场中第j列指标综合评价值，ωj表示第j个指标的综合权重系数。步骤3：求取电力市场运行效果评价矩阵差数列矩阵其中δcstij＝|cst0j-cstij|(i＝1,2,l,m；j＝1,2,l,n)(103)式中：δcmai表示第i个电力市场综合运行效果评价向量与理论运行状态下运行效果评价向量的差异向量。步骤4：求取每个市场下每个指标与理论运行状态下相应指标的灰色关联系数式中，δm为电力市场运行效果评价矩阵差数列矩阵中最小的值即δm为电力市场运行效果评价矩阵差数列矩阵中最大的值即ρ为分辨系数，取值范围为[0,1]，影响灰色关联系数ξij的整体水平上的数值大小，但是对最终的关联系数排序没有影响，一般取经验值0.618。步骤5：求取每个市场与理论运行状态下市场的关联度步骤6：将得到的关联度γi进行从大到小顺序的排序，得到关于i个电力市场运行情况从优到劣的排序，并得到一个相对评分值即关联度的数值γi。下面结合实例说明在电力现货市场评价体系中筛选部分适应于中长期交易的指标构成新的指标体系，由于该指标体系中指标数量较小，且指标涉及的方面较多，所以不再进行细分层次，具体指标与数据如表10所示：表10广东电力市场与云南电力市场中长期交易部分原始数据将数据进行标准化后得到如表11所示结果：表11广东电力市场与云南电力市场中长期交易部分标准化数据参考电力市场方面的教授以及规则制定者意见，利用专家打分法得到各个指标权重系数向量为：p1＝[0.12,0.08,0.15,0.19,0.04,0.12,0.04,0.04,0.22]利用相关系数法得到各个指标权重系数向量为：p2＝[0.10,0.12,0.10,0.11,0.10,0.11,0.12,0.12,0.12]利用基于层次分析法的熵值法得到各个指标权重系数向量为：p3＝[0.07,0.01,0.07,0.07,0.00,0.12,0.03,0.00,0.62]利用基于博弈论的综合指标权重确定方法得到最终的综合权重系数向量为：pres＝[0.12,0.08,0.14,0.18,0.04,0.12,0.05,0.04,0.23]将不同权重赋值方法得到的权重系数进行比较如附图3所示，从图中可以看到，相关系数分析法给出的权重系数大小较为一致，说明该组数据中没有出现需要进行特别留意的关键性指标数据；基于层次分析法的熵值法对于市场开放程度u2、装机容量增长率u5、需求量增长率u8以及市场成员数目增长率u9的赋值较为极端，对u2权重赋值为0.01，对u5与u8权重赋值为0，对u9权重赋值为远超于平均水平的0.62，查看数据以及判断矩阵发现，这是因为u2、u5与u8在判断矩阵中的重要程度较低，导致其在层次分析法中权重系数较低；同时数据之间的差异性也比较小，使得其在熵值法的权重赋值中权重系数也比较小，这导致其组合权重系数将会变得十分小，甚至为零。而u9则相反，在层次分析法与熵值法中的权重赋值均较大，导致其组合权重远超平均水平。虽然从权重系数分配的角度来说是合理的，但是在实际的评价体系中，这样的权重系数分配过于偏激，会产生市场评估得分过低的情况，不太实用，这也是基于层次分析法的熵值法的局限性。而基于博弈论的组合权重确定方法则能够弥补该方面的不足，从图3中可以清晰的看到，权重系数整体分配上更加合理，没有出现基于层次分析法的熵值法对u9赋予0.64远超平均水平的权重系数的情况，说明基于博弈论的综合权重确定方法的实际应用情况将会更好。同时，该结果与专家打分法结果接近，说明该结果能够得到专家的一致认同，结果是十分合理的。利用灰色关联度对广东电力市场以及云南电力市场中长期交易部分运行情况与理论最佳运行情况进行比较计算得到如下结果：表12广东电力市场与云南电力市场中长期交易部分灰色关联度分析结果由灰色关联度可以得到，云南电力市场中长期交易情况略优于广东电力市场，实际上，国内对于云南电力市场建设成果也给予了较高评价，与本文方法分析结果一致。广东是我国最先一批建设电力市场的省份之一，也是目前为止我国电力市场建设走在最前沿的省份，现阶段广东电力市场已经开始进行电力现货市场实时交易的试运行，领先于目前处于日前市场建设的云南电力市场。而广东电力市场中长期交易部分运行情况略低于云南电力市场的结果表明广东电力市场建设过程中得到的经验教训成功地被推广，上一阶段的建设是有着显著成果的；同时也表明云南电力市场进行下一阶段日前市场建设的决定是正确的，符合市场实际情况与要求。对云南的电力市场数据进行分析发现云南电力市场具有与众不同的特点。云南电力市场新能源占比较高，市场开放程度较高，电价较低，但是电价波动情况较大。这是因为云南的能源结构中主要由水电构成，占比达69％以上，云南整体对于水利资源的开发利用较大。由于云南属于季风气候，具有明显的季节性干湿特点，夏天处于汛期，可发电量过大，导致电价的下降，而在冬天则由于处于旱期，可发电量减小，电价则上升。一年的电价具有明显的季节特点，在夏天低至0.11元/千瓦时，在冬天高至0.22元/千瓦时，电价波动较大。同时，在夏天，水电站又采取“弃水保价”的措施，造成资源的大量浪费。所以，如何在夏天汛期保证较大的需求消纳也将是下一步云南电力市场建设的重点之一。主要可以从两个方面入手：一是在已有的较高开放程度上继续提升开放程度，依靠出口电量来保证汛期电量的充分消纳，将来也可以作为区域电力市场提升开放程度的典型案例推广到全国进行学习；二是拉动区域内经济的发展，云南相较于其东边的广东省来说经济水平并不算太高，还有很多潜力空间值得开发，电力市场可以通过对用电侧的额外补贴来刺激需求与吸引投资，带动全省的经济发展，并从中获益。当前第1页12