一种获得玻璃材料结构松弛参数的方法与流程

技术领域：

本发明涉及材料性能参数测试领域，尤其涉及一种获得玻璃材料结构松弛参数的方法。

背景技术：
：

汽车玻璃成型是将玻璃原片经加热炉加热到玻璃化转变温度以上的软化状态后，通过各种工艺成型，例如自重、bt、gt等。玻璃在软化状态属于粘弹性体，对其材料力学性能的准确表征，关系到玻璃成型的型面、工艺、模具等关键技术的开发，是玻璃产品成型技术的研究基础，目前使用最普遍的是粘弹性本构。粘弹性本构模型中涉及两类松弛，即应力松弛和结构松弛。对应力松弛和应力松弛参数的获取方法已经相对成熟。然而对结构松弛及其参数获取的实验方法却研究甚少。结构松弛是玻璃等材料处于玻璃化转变区时玻璃态时，处于热力学的非平衡态，会自发的向平衡态的结构松弛的过程。对于有钢化的成型方式，由于玻璃收到急冷淬火，成型时含有大量的结构松弛，会造成明显的回弹和钢化应力，因此需考虑结构松弛对成型的影响。

玻璃结构松弛通常用tool-narayanawamy-moynihan(tnm)模型描述，该模型中包含四个参数，分别是指前因子τ0，结构松弛活化能与理想气体常数比值-δh^*/r，非线性参数x，以及非指程度β。有两种实验方法可以获得tnm模型参数，一种是基于dsc差示扫描量热仪的比热测试方法，一种是基于dil热膨胀仪的膨胀系数测试方式。

本发明采用的参数获取方法是基于dsc的比热测试方法，与其他学者研究光学玻璃材料结构松弛dsc测试的区别主要表现在获取参数-δh^*/r上，这个参数不是某一个松弛单元特有的，而是多个松弛单元协同运动必须具备的活化焓，不能直接利用单条比热曲线获得的-δh^*/r(这种方式得到的值偏小)，其他学者通常利用材料的高温黏度测试，通过vogel-fulcher-tammann模型换算出-δh^*/r，不仅费时费力，设备也很昂贵。本发明利用moynihan提出的极限假想温度与降温速率之间的关系，在此结构松弛参数获取方法上做了大量改进。

虽然有学者在研究药品冷冻干燥材料(例如丙三醇)的结构松弛性能中提到可以用moynihan关系确定-δh^*/r，但是本专利提出的将-δh^*/r这个参数固定，然后通过最小二乘方法寻找其余三个参数最优解的方法，尚属首创。研究药品冷冻干燥材料结构松弛参数属于材料的低温性能，而本专利针对的汽车玻璃结构松弛属于材料的高温性能，研究对象的不同使得研究方法、使用仪器等存在明显的差别。

本发明是在集成了上述光学玻璃研究和冷冻干燥材料研究各自的优点的基础上提出的一种获得玻璃材料结构松弛参数的方法。

技术实现要素：
：

本发明针对现有技术存在的上述技术问题，提供获得玻璃材料结构松弛参数的方法，不仅省去了费时费力的高温黏度测试，以及昂贵的高温黏度测试设备，同时大大提高了结构松弛参数的获得的便捷性、可靠性。

本发明所采取的技术方案是：

一种获得玻璃材料结构松弛参数的方法，其特征在于包含以下步骤：

步骤1，利用差示扫描量热仪获得至少两个不同降温速率下的降温比热曲线，通过降温比热曲线换算获得每个降温速率下的极限假想温度t′f；

步骤2，通过极限假想温度与降温速率之间的关系式：计算得到-δh^*/r，式中q为降温速率，t′f为极限假想温度，-δh^*/r为结构松弛活化能与理想气体常数比值；

步骤3，对步骤1中获得的降温比热曲线进行无量纲处理得到实验无量纲比热

步骤4，基于tnm模型获得理论无量纲比热所述理论无量纲比热中包括指前因子τ0，结构松弛活化能与理想气体常数比值-δh^*/r，非线性参数x以及非指程度β；

步骤5，将步骤1中获得的-δh^*/r代入步骤4中的理论无量纲比热，以理论无量纲比热对实验无量纲比热进行非线性最小二乘拟合，通过最优化方法计算寻找τ0、x、β的最优解；

步骤6，将上述步骤中得到的-δh^*/r和τ0、x、β的最优解代入计算机软件中，计算得到结构松弛参数。

在一种可能的实施方式中，步骤1中每个降温比热曲线包括位于降温比热曲线两端的玻璃段比热曲线和液态段比热曲线，将所述降温比热曲线积分得到焓曲线。

在一种可能的实施方式中，所述焓曲线包括分别与玻璃段比热曲线和液态段比热曲线相对应的玻璃段焓曲线和液态段焓曲线，将所述玻璃段焓曲线和液态段焓曲线延长，两者交点对应的温度，即为极限假想温度t′f。

在一种可能的实施方式中，在步骤3中对玻璃段比热曲线和液态段比热曲线进行线性拟合，通过公式进行无量纲处理得到实验无量纲比热式中cpg(t)和cpl(t)分别表示玻璃段比热曲线和液态段比热曲线拟合后的直线，cp(t)为实验测得的比热值。

在一种可能的实施方式中，步骤5中以理论无量纲比热表达式拟合实验的无量纲比热得到tnm模型的最优解所使用的公式为n和n分别表示降温比热曲线的数目和每条降温比热曲线上的离散点数，wi表示权重，用以平衡每条降温比热曲线在优化过程中的贡献。

本发明由于采取了上述技术方案，其具有如下有益效果：

本发明的一种获得玻璃材料结构松弛参数的方法，使用的是常见的差示扫描量热仪，省去了费时费力的高温黏度测试以及昂贵的高温黏度测试设备，同时大大提高了结构松弛参数的获得的便捷性、可靠性，对于不同的玻璃材料可以很方便地重复此方法获得结构松弛参数。

附图说明：

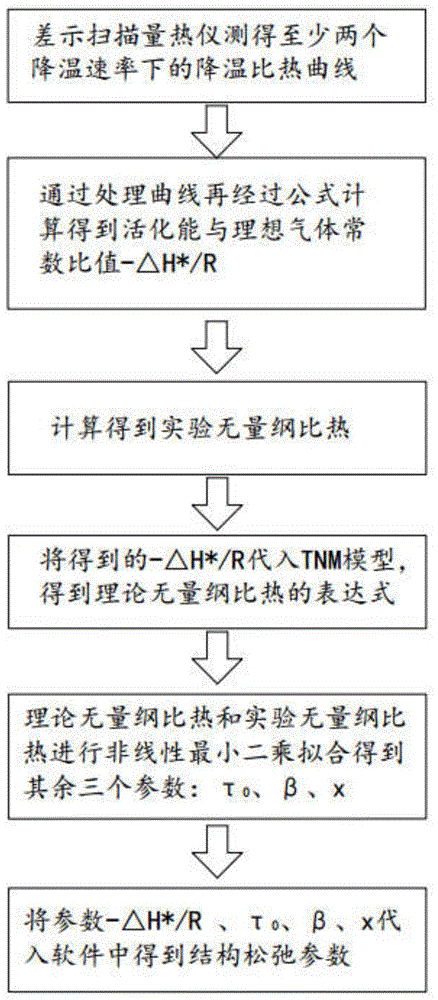
图1为本发明的方法流程图；

图2为本发明中的降温比热曲线和将降温比热曲线积分得到的焓曲线示意图。

标号说明：

1、玻璃段比热曲线，2、液态段比热曲线，3、玻璃段焓曲线，4、液态段焓曲线。

具体实施方式：

为详细说明本发明的技术内容、所实现目的及效果，下面将结合附图与实施方式对本发明做进一步的说明，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。

如图1所示，为本发明提供的一种获得玻璃材料结构松弛参数的方法，该方法包含以下步骤：

步骤1，选择合适的检测设备，由于玻璃的玻璃化转变温度较高，普通的dsc设备最大只能达到650℃，而汽车玻璃的液态段通常在650℃以上，因此需要选择高温dsc差示扫描量热仪，例如dsc404f或者setaram96line，调试校准dsc差示扫描量热仪，利用差示扫描量热仪获得至少两个不同降温速率下的降温比热曲线，通过降温比热曲线换算获得每个降温速率下的极限假想温度t′f；

步骤2，通过极限假想温度与降温速率之间的关系式：

通过公式(1)计算得到-δh^*/r，式中q为降温速率，t′f为极限假想温度，-δh^*/r为结构松弛活化能与理想气体常数比值，由于-δh^*/r与降温速率q和t′f的函数关系，可以知道测试越多不同降温速率下的降温比热曲线，实验中所得到的-δh^*/r值越精确；

由于汽车玻璃钢化速率很快，实验选取的降温速率应尽可能的大，范围要宽，本发明优选的具体实验条件为在同一升温速率10℃/min下加热至800℃，然后分别以20、50、100、150、200℃/min的降温速率从800℃降温至300℃即可(汽车玻璃的玻璃化转变温度在610℃左右)。

步骤3，对步骤1中获得的降温比热曲线进行无量纲处理得到实验无量纲比热所谓无量纲处理即为归一化处理，使降温比热曲线转变为一个最大值为1的曲线；

步骤4，基于tnm模型获得理论无量纲比热所述理论无量纲比热中包括指前因子τ0，结构松弛活化能与理想气体常数比值-δh^*/r，非线性参数x以及非指程度β，tnm模型即tool-narayanawamy-moynihan模型，是一个现有技术，通过tnm模型得到的是理论计算得出的无量纲比热数值，在这里得到的理论无量纲比热是一个关于-δh^*/r和τ0、x、β的表达式；

步骤5，将步骤1中获得的-δh^*/r代入步骤4中的理论无量纲比热，以理论无量纲比热对实验无量纲比热进行非线性最小二乘拟合，通过最优化方法计算寻找τ0、x、β的最优解，固定了-δh^*/r的数值从而得到其他参数的值；

步骤6，将上述步骤中得到的-δh^*/r和τ0、x、β的最优解代入计算机软件中，计算得到结构松弛参数，计算机计算仿真软件如abaqus等具有成熟的建模和计算功能，其中玻璃材料结构松弛参数的得到需要上述四个参数，通过上述步骤得到的四个参数输入到软件中，便可得到所需的玻璃材料结构松弛参数。

通常情况下通过dsc差示扫描量热仪可以直接得到计算玻璃材料结构松弛参数所需的四个参数-δh^*/r和τ0、x、β，但是实践中发现如此得到的玻璃材料结构松弛参数与实际情况存在出入。因此提出一种获得玻璃材料结构松弛参数的方法，通过本发明的方法计算得到的结构松弛参数更加符合生产实践过程的结果，相比于其他的测试方法，本发明的方法省去了费时费力的高温黏度测试以及昂贵的高温黏度测试设备，同时大大提高了结构松弛参数的获得的便捷性、可靠性，对于不同的玻璃材料可以很方便地重复此方法获得结构松弛参数。

如图2所示为通过差示扫描量热仪得到的降温比热曲线，以及通过对降温比热曲线积分得到的焓曲线，降温比热曲线中横坐标为温度t，纵坐标为比热c值cp(t)；焓曲线中纵坐标变为焓h。

其中，步骤1中每个降温比热曲线包括位于降温比热曲线两端的玻璃段比热曲线1和液态段比热曲线2，将所述降温比热曲线积分得到焓曲线。其中，所得到的焓曲线具有与降温比热曲线两端的玻璃段比热曲线1和液态段比热曲线2相对应的玻璃段焓曲线3和液态段焓曲线4。当温度处于玻璃段中，玻璃为固态的玻璃态；而当温度处于液态段中，玻璃为融化的液态。玻璃段焓曲线3和液态段焓曲线4近似于一条直线，将两者延长，交点对应的温度即为极限假想温度t′f，随后在步骤2中使用步骤1得到的数值计算得到-δh^*/r。

在步骤3中对玻璃段比热曲线1和液态段比热曲线2进行线性拟合，通过公式

对试验测得的比热进行无量纲处理得到实验无量纲比热式中cpg(t)和cpl(t)分别表示玻璃段比热曲线1和液态段比热曲线2拟合后的直线，是通过对曲线起点和终点的位置做切线得到的拟合直线，cp(t)为实验设备记录的比热值。

其中，在步骤4中通过tnm模型得到的是理论无量纲比热的表达式

其中

所述的tnm模型即为公式(3)(4)(5)的组合，用以表达和计算理论无量纲比热理论无量纲比热容包含四个结构松弛模型参数指前因子τ0，结构松弛活化能与理想气体常数比值-δh^*/r，非线性参数x，以及非指程度β，其中-δh^*/r使用上述步骤2中计算得到的数值代入；另外δti为温度步长，通常取1k；i、j、k代表数值积分的离散点；q是实验采用的降温速率。

其中，在步骤5中，拟合实验无量纲比热得到tnm模型的最优解所使用的公式为：

公式(6)为使用最小二乘法拟合实验无量纲比热和理论无量纲比热的计算公式，其中n和n分别表示降温比热曲线的数目和每条降温比热曲线上的离散点数，wi表示权重，用以平衡每条降温比热曲线在优化过程中的贡献。将其导入计算机仿真计算软件中进行优化调整，在固定了从而得到三个参数τ0、x、β的最优解。

最后一步中，将上述过程中得到的四个参数，输入到计算机仿真计算软件如abaqus中，便可得到所需的玻璃材料结构松弛参数。

上述说明仅为提供本发明较好的实施方式，并非对本发明的限制，本发明也不仅限于上述举例，本技术领域的普通技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也属于本发明的保护范围。