渐开线斜齿轮副齿宽修形动力学模型建立方法与流程

本发明涉及机械动力学技术领域，特别是涉及一种渐开线斜齿轮副齿宽修形动力学模型建立方法。

背景技术：

斜齿轮是大功率重载齿轮，对齿轮的强度要求比较高，对于存在齿向啮合偏差载荷分布不均的齿轮副，轮齿啮合中心并不在齿面齿宽方向的齿轮中间，甚至在齿轮运动过程中，啮合中心在齿宽方向左右变动。因此，难以分析这种由齿宽方向不均引起的齿轮副动态特性规律。

因此，如何提高齿宽方向不均的齿轮副动态特性准确性为本领域技术人员亟待解决的技术问题。

技术实现要素：

有鉴于此，本发明目的是提供一种渐开线斜齿轮副齿宽修形动力学模型建立方法，能够提高齿宽方向不均的齿轮副动态特性准确性。

为了达到上述目的，本发明提供如下技术方案：

一种渐开线斜齿轮副齿宽修形动力学模型建立方法，包括以下步骤：

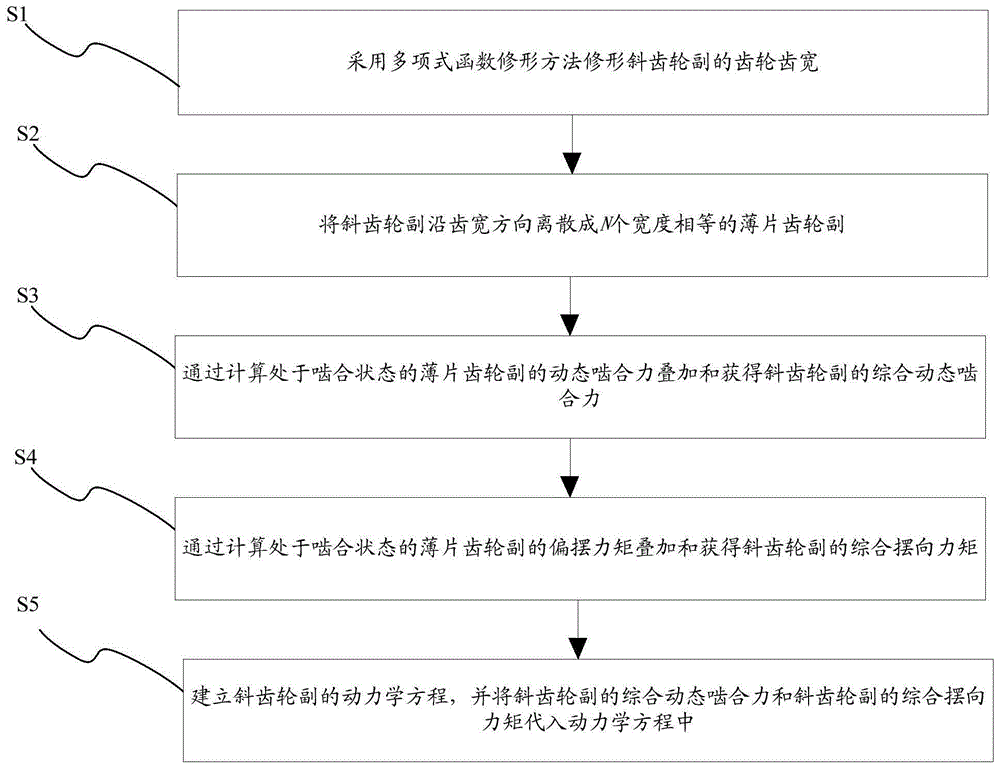
采用多项式函数修形方法修形斜齿轮副的齿轮齿宽；

将所述斜齿轮副沿齿宽方向离散成n个宽度相等的薄片齿轮副；

通过计算处于啮合状态的所述薄片齿轮副的动态啮合力叠加和获得所述斜齿轮副的综合动态啮合力；

通过计算处于啮合状态的所述薄片齿轮副的偏摆力矩叠加和获得所述斜齿轮副的综合摆向力矩；

建立所述斜齿轮副的动力学方程，并将所述斜齿轮副的综合动态啮合力和所述斜齿轮副的综合摆向力矩代入所述动力学方程中。

在一个具体实施方案中，所述多项式函数的修形量公式为：

式中，δd,i代表齿宽方向任意位置修形量，di为所述斜齿轮齿面上距离中心位置长度，s为多项式函数的弯曲指数，b为齿向修形长度，δd为齿向修形量，d为齿宽，1≤s≤5。

在另一个具体实施方案中，处于啮合状态的所述薄片齿轮副的齿轮瞬时压力角为：

αl＜αt,i＜αu；

αl为所述斜齿轮的最小压力角，αt,i为所述薄片齿轮副的齿轮瞬时压力角，i＝1,2分别代表所述斜齿轮副中的两个斜齿轮，αu为所述斜齿轮的最大压力角。

在另一个具体实施方案中，所述斜齿轮副的综合动态啮合力计算公式为：

式中，为所述斜齿轮副的综合动态啮合力，fm,i为第i对薄片齿轮副在啮合线方向上的动态啮合力。

在另一个具体实施方案中，每对薄片齿轮副在啮合线方向上的动态啮合力计算公式为：

式中，i＝1,…,n，代表第i对薄片齿轮副，ke为第i对薄片齿轮副的时变啮合刚度，为第i对薄片齿轮副啮合阻尼，m1和m2分别为斜齿轮副的模数，x1、x2、y1、y2、z1、z2分别为斜齿轮副两个斜齿轮在坐标系上的坐标位置，rb1和rb2分别为斜齿轮副两个斜齿轮的半径；

δi(b,δit)为第i对薄片齿轮副的啮合线变形量，为第i对薄片齿轮副的啮合线变形量的一阶导数，δi(t)为第i对薄片齿轮副的动态传递误差，为第i对薄片齿轮副的动态传递误差的一阶导数；

γ为符号函数，γ＝1代表齿面啮合，γ＝-1代表齿背啮合，αi为第i对薄片齿轮副的动态啮合角，γi为第i对薄片齿轮副的任意时刻相对位置角；

ei为第i对式薄片齿轮副的综合误差及齿轮修形引起的齿形偏差，es,i为第i对式薄片齿轮副齿廓齿形误差，ep,i为第i对式薄片齿轮副齿轮装配误差在啮合线上投影的等效值，em,i为制造加工、安装及磨损引起轴承、箱体零件变形导致传动轴不平行，引起齿宽方向的误差，eβ,i为第i对薄片齿轮副齿向修形引起的齿形偏差。

在另一个具体实施方案中，

式中，δi(t)≥bcosβb时为齿面啮合状态，δi(t)≤-bcosβb时为齿背啮合状态，其余为脱齿状态。

在另一个具体实施方案中，所述es,i的计算公式为：es,i＝e0,i+er,isin(2πωt)，e0，i＝0，fpd,i为齿轮基节偏差，ff,i为齿形公差；

所述ep,i的计算公式为：ep,i＝ap,isin(αi+γγ)；

所述em,i的计算公式为：

所述eβ,i的计算公式为：

在另一个具体实施方案中，所述斜齿轮副的综合摆向力矩计算公式为：

tm,i＝fm,i·di；

tm,i为第i对薄片齿轮副所受的偏摆力矩。

在另一个具体实施方案中，所述斜齿轮副包括第一齿轮和第二齿轮；

所述第一齿轮的动力学方程为：

所述第二齿轮的动力学方程为：

t1、t2分别为系统的输入与负载扭矩，kix、kiy、kiz和cix、ciy、ciz分别为各个齿轮中心轴承刚度与阻尼，ixi,iyi,izi分别为齿轮绕x，y和z轴转动惯量，i＝1,2。

在另一个具体实施方案中，为齿面啮合摩擦力，μ为齿面摩擦系数。

根据本发明的各个实施方案可以根据需要任意组合，这些组合之后所得的实施方案也在本发明范围内，是本发明具体实施方式的一部分。

根据上述技术方案可知，本发明提供的渐开线斜齿轮副齿宽修形动力学模型建立方法，采用多项式函数修形方法修形斜齿轮副的齿轮齿宽，能够更准确地体现出齿宽方向不同位置的载荷不均导致齿面变形；此外，本发明通过将斜齿轮副沿齿宽方向离散成n个宽度相等的薄片齿轮副，将啮合状态的薄片齿轮副的动态啮合力叠加在一起获得斜齿轮副的综合动态啮合力，将处于啮合状态的薄片齿轮副的偏摆力矩叠加在一起获得斜齿轮副的综合摆向力矩，并将将斜齿轮副的综合动态啮合力和斜齿轮副的综合摆向力矩代入动力学方程中，得到渐开线斜齿轮副齿宽修形动力学模型，提高了齿宽方向不均的齿轮副动态特性准确性。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1是本发明提供的一种渐开线斜齿轮副齿宽修形动力学模型建立方法流程图；

图2是本发明提供的斜轮齿齿宽修形参数示意图；

图3是本发明提供的齿轮薄片切割示意图；

图4为本发明提供的齿轮角度示意图；

图5是本发明提供的斜齿轮分布啮合三维动力学模型；

图6为本发明提供的不同修形量下的载荷分配因子kh曲线图；

图7是本发明提供的不同弯曲指数下的载荷分配因子kh曲线图；

图8是本发明提供的齿向动载系数kβ随修形量变化关系图；

图9为本发明提供的齿向动载系数kβ随转速变化关系图；

图10是本发明提供的齿向动载系数kβ随负载变化关系图；

图11是本发明提供的三维齿面接触应力图；

图12为本发明提供的齿面应力投影图；

图13是本发明提供的齿宽修形量δd＝0时，齿面应力分布三维图；

图14是本发明提供的齿宽修形量δd＝0时，齿面应力分布二维等高线图；

图15是本发明提供的齿宽修形量δd＝8μm时，齿面应力分布三维图；

图16是本发明提供的齿宽修形量δd＝8μm时，齿面应力分布二维等高线图；

图17是本发明提供的齿宽修形量δd＝16μm时，齿面应力分布三维图；

图18是本发明提供的齿宽修形量δd＝16μm时，齿面应力分布二维等高线图；

图19是本发明提供的齿宽修形量δd＝24μm时，齿面应力分布三维图；

图20是本发明提供的齿宽修形量δd＝24μm时，齿面应力分布二维等高线图；

图21是本发明提供的弯曲指数s＝1.5时，齿面应力分布三维图；

图22是本发明提供的弯曲指数s＝1.5时，齿面应力分布二维等高线图；

图23是本发明提供的弯曲指数s＝2时，齿面应力分布三维图；

图24是本发明提供的弯曲指数s＝2时，齿面应力分布二维等高线图；

图25是本发明提供的弯曲指数s＝2.5时，齿面应力分布三维图；

图26是本发明提供的弯曲指数s＝2.5时，齿面应力分布二维等高线图；

图27是本发明提供的弯曲指数s＝3时，齿面应力分布三维图；

图28是本发明提供的弯曲指数s＝3时，齿面应力分布二维等高线图。

具体实施方式

为了使本领域的技术人员更好的理解本发明的技术方案，下面结合附图和具体实施方式对本发明作进一步的详细说明。

如图1所示，本发明公开了一种渐开线斜齿轮副齿宽修形动力学模型建立方法，包括以下步骤：

步骤s1：采用多项式函数修形方法修形斜齿轮副的齿轮齿宽。

需要说明的是，对齿宽进行综合修形，在斜齿轮副的齿轮齿宽方向左右两边采用相同的修形参数，即包含齿向修形量δd，齿向修形长度b以及齿向修形曲线如图2所示。

具体地，本发明公开了多项式函数的修形量公式为：

式中，δd,i代表齿宽方向任意位置修形量，di为斜齿轮齿面上距离中心位置长度，s为多项式函数的弯曲指数，b为齿向修形长度，δd为齿向修形量，d为齿宽，1≤s≤5。

对于另一啮合齿轮，通常采用相同的修形参数进行修形。这样，可以用包含3个参数的参数集p表示单个齿轮的齿宽修形，p∈{δd,b,s}。

步骤s2：将斜齿轮副沿齿宽方向离散成n个宽度相等的薄片齿轮副。

对于存在齿向啮合偏差的载荷分布不均的齿轮副，轮齿啮合中心并不在齿面齿宽方向的齿轮中间，甚至在齿轮运动过程中，啮合中心在齿宽方向左右变动。采用常规方法无法准确分析轮齿啮合力在齿宽方向的载荷响应分布。本发明通过建立更精确的啮合模型来分析这种由齿宽方向不均引起的齿轮系统动态特性规律。

斜齿轮副相对于直齿轮副来说，唯一的根本区别就是斜齿系统设计中包含螺旋角参数β。从另一角度来看，直齿轮副是一种特殊的斜齿轮，即螺旋角值β＝0°。因此，将斜齿轮沿齿宽方向离散成n个宽度相等的薄片，如图3所示，每一个薄片都是一对齿宽较小的斜齿轮，齿宽为δl，螺旋角为β，每一个薄片轮齿的啮合刚度(i＝1,…,n)。

步骤s3：通过计算处于啮合状态的薄片齿轮副的动态啮合力叠加和获得斜齿轮副的综合动态啮合力。

对于单对齿轮副，只要确定了啮合位置，齿轮的啮合刚度便可求得。然而对于斜齿轮，进行薄片切割后的一系列薄片斜齿轮副，不仅要确定每个薄片的啮合位置，还要确定各个薄片是否处于啮合状态，所以确定各个薄片轮齿是否处于啮合十分重要。如图4所示，以第一齿轮输入角速度ω1驱动第二齿轮为例。为定值，且可以表示为：

式中，t为时间，为的初始最小角相位。

各切片齿轮中的和(i＝1,2分别为第一齿轮和第二齿轮)的大小可以分别表示为；

其中，i为处于啮合的齿轮的编号，i＝1,…,n。α'0代表齿轮的端面压力角。di表示各薄片齿轮的轴向坐标位于薄片轮齿的中间，l为齿轮副的中心距，β表示斜齿轮副的螺旋角。

各薄片轮齿的瞬时压力角为：处于啮合状态的薄片齿轮副的齿轮瞬时压力角为：αl＜αt,i＜αu。αl为斜齿轮的最小压力角，αt,i为薄片齿轮副的齿轮瞬时压力角，i＝1,2分别代表斜齿轮副中的两个斜齿轮，αu为斜齿轮的最大压力角。

进一步地，本发明公开了斜齿轮副的综合动态啮合力计算公式为：式中，为斜齿轮副的综合动态啮合力，fm,i为第i对薄片齿轮副在啮合线方向上的动态啮合力。

具体地，本发明公开了每对薄片齿轮副在啮合线方向上的动态啮合力计算公式为：

式中，i＝1,…,n，代表第i对薄片齿轮副，ke为第i对薄片齿轮副的时变啮合刚度，为第i对薄片齿轮副啮合阻尼，m1和m2分别为斜齿轮副的模数，x1、x2、y1、y2、z1、z2分别为斜齿轮副两个斜齿轮在坐标系上的坐标位置，rb1和rb2分别为斜齿轮副两个斜齿轮的半径。δi(b,δit)为第i对薄片齿轮副的啮合线变形量，为第i对薄片齿轮副的啮合线变形量的一阶导数，δi(t)为第i对薄片齿轮副的动态传递误差，为第i对薄片齿轮副的动态传递误差的一阶导数。γ为符号函数，γ＝1代表齿面啮合，γ＝-1代表齿背啮合，αi为第i对薄片齿轮副的动态啮合角，γi为第i对薄片齿轮副的任意时刻相对位置角。ei为第i对式薄片齿轮副的综合误差及齿轮修形引起的齿形偏差，es,i为第i对式薄片齿轮副齿廓齿形误差，ep,i为第i对式薄片齿轮副齿轮装配误差在啮合线上投影的等效值，em,i为制造加工、安装及磨损引起轴承、箱体零件变形导致传动轴不平行，引起齿宽方向的误差，eβ,i为第i对薄片齿轮副齿向修形引起的齿形偏差。

本发明充分考虑了斜齿轮副啮合时存在的各种误差，进一步提高了修形精度。

具体地，本发明公开了式中，δi(t)≥bcosβb时为齿面啮合状态，δi(t)≤-bcosβb时为齿背啮合状态，其余为脱齿状态。

进一步地，本发明具体公开了es,i的计算公式为：es,i＝e0,i+er,isin(2πωt)，e0，i＝0，fpd，i为齿轮基节偏差，ff，i为齿形公差；

ep,i的计算公式为：ep,i＝ap,isin(αi+γγ)；

em,i的计算公式为：

eβ,i的计算公式为：

步骤s4：通过计算处于啮合状态的薄片齿轮副的偏摆力矩叠加和获得斜齿轮副的综合摆向力矩。

斜齿轮副的综合摆向力矩计算公式为：tm,i＝fm,i·di；tm,i为第i对薄片齿轮副所受的偏摆力矩。

步骤s5：建立斜齿轮副的动力学方程，并将斜齿轮副的综合动态啮合力和斜齿轮副的综合摆向力矩代入动力学方程中。

如图5所示，具体地，本发明公开了斜齿轮副包括第一齿轮和第二齿轮，第一齿轮的动力学方程为：

第二齿轮的动力学方程为：

t1、t2分别为系统的输入与负载扭矩，kix、kiy、kiz和cix、ciy、ciz分别为各个齿轮中心轴承刚度与阻尼，ixi,iyi,izi分别为齿轮绕x，y和z轴转动惯量，i＝1,2。

进一步地，本发明公开了为齿面啮合摩擦力，μ为齿面摩擦系数。

为了证明本发明公开的方法的准确性，本发明通过对斜齿轮副的齿宽方向动态载荷分布状态进行分析来验证，定义各薄片齿轮副的动态载荷分配因子和齿轮系统齿向动态载荷系数，各表达式分别下：

式中，(fm,i)rms为第i对薄片齿轮副动态啮合力的均方根值，[(fm,i)rms]max为薄片齿轮副动态啮合力的均方根值的最大值，fn为准静态条件下齿面所受实际载荷，n为切片后处于啮合状态的薄片齿轮副总数。其中，动态载荷分配因子是与各薄片齿轮副齿面所受动态啮合力相关的参数，可以表征齿轮副动态载荷在齿宽方向分布状态；齿向动态载荷系数是与各薄片齿轮副齿面所受动态载荷均值及最大载荷相关参数，可以用来表达斜齿轮副动态载荷在齿宽方向分布的不均匀程度。

实施例一

在输入转速为2000r/min，负载扭矩为100nm的工况下，修形长度b＝d/2(即全齿宽修形)，s多项式函数的弯曲指数s＝2的条件下，研究了不同修形量下动态载荷分配因子在齿宽方向的分布状态，结果如图6所示。其中，齿宽最大修形量δd取值分别为[0μm,8μm,16μm,24μm]。从图中可以看出，在无修形状态下，由于齿轮安装、轴承变形等误差导致实际工作中，齿宽方向受载不均。载荷最大值(kh,i＝1.41)集中在齿宽方向的一端，最小值(kh,i＝0.62)集中在齿宽另一端。随着修形量的增大，齿宽方向的载荷最大值逐渐靠近齿面的中心位置，且最大载荷分配因子逐渐减小。在齿宽修形量为δd＝24μm的状态下，最大载荷分配因子位于距齿宽中心4.2mm处。此时，最大载荷分配因子为kh,i＝1.19，相比较标准状态下的齿轮副，齿宽方向的载荷波动幅值得到显著降低。从结果可以看出，采用齿宽修形方法，在适当的修形量下，可以改善齿面载荷过于集中的状态；同时可以改变齿向载荷分布中心，使得齿向载荷中心逐渐靠近齿面中心位置。

在该工况下，修形长度b＝d/2，齿宽最大修形量δd＝24μm的条件下，不同多项式函数的弯曲指数下动态载荷分配因子在齿宽方向的分布状态，结果如如图7所示。其中，弯曲指数s取值分别为[1.5,2,2.5,3]。从图中可以看出，弯曲指数的变化不会显著改变齿向动态载荷的最大值与最小值，也不会对齿向载荷分布中心有较大影响，但会影响动态载荷在齿宽方向的分布形状。随着弯曲指数的逐渐增大，齿向动态载荷分布中心位置附近的载荷变化逐渐平缓，载荷分布较为均匀。相比于弯曲指数较小的修形曲线，齿向动态载荷的最大值稍有降低。从结果可以看出，采用齿宽修形方法，在不同的多项式函数的弯曲指数下，齿向动态载荷中心位置不会有明显变化，但是会影响载荷中心位置附近的载荷变化曲率。也就是说，在该工况下，采用较大的多项式函数的弯曲指数，可以使得载荷中心位置附近载荷分布较为均匀。

在相同的转速及载荷工况下，不同多项式函数的弯曲指数条件下齿宽修形量对齿向动态载荷系数的影响规律，结果如图8所示。其中，弯曲指数s取值分别为[1.5,2,2.5,3]，修形长度b＝d/2。从图中可以看出，对于每一个弯曲指数，都存在一个最优修形量，使得动态载荷系数达到最优值，且最优修形量都在23μm左右。其次，可以看出，最优修形量下，弯曲指数s＝3时的动态载荷系数最优能达到1.64左右；弯曲指数s＝1.5时的动态载荷系数最优能达到1.81左右。这表明最优修形量下，较大的弯曲指数能够一定程度上降低斜齿轮副动态载荷在齿宽方向分布的不均匀的状态。此外，从图中还可以得出，当采取较小的齿宽修形量时(修形量δd＜9μm)，采用较大的弯曲指数会使得修形效果不如较小的弯曲指数对应的修形齿轮。当需要采用较小修形量时，采用弯曲指数较低的修形曲线会使得修形效果更佳。

负载扭矩为100nm的工况下，在弯曲指数s＝3，修形长度b＝d/2的条件下，不同齿宽修形量下的齿轮系统齿向动载系数随转速的变化规律如图9所示。其中，齿宽最大修形量δd取值分别为[0μm,8μm,16μm,24μm]，转速变化范围为[100r/min，2500r/min]。从结果可以看出，不同修形量下，随转速的增大，齿向动载系数均是呈逐渐增大最后趋于稳定的变化趋势。相比于无修形的标准齿轮系统，采用齿向修形后的齿轮副均能在整个转速工作范围内实现对动态载荷降低的效果。且随着转速的升高，修形后的齿轮齿向动态载荷降低越明显。在转速为2500r/min时，采用齿向修形量为δd＝24μm的齿轮副修形效果最为显著，此时齿向动态载荷系数为1.96，相比于无修形状态下的结果(kβ＝2.21)，修形使得齿向动载系数降低了11.31％。

在输入转速为2000r/min的工况下，齿宽修形量为δd＝24μm，修形长度b＝d/2的条件下，多项式函数的弯曲指数下的齿轮系统齿向动载系数随负载扭矩的变化规律结果如图10所示。其中，多项式函数的弯曲指数s取值分别为[1.5,2,2.5,3]，负载变化范围为[0nm，800nm]。从结果可以看出，当载荷较大的条件下，采用较小的弯曲指数能够更好地降低齿向动载系数。负载为800nm时，弯曲指数s＝1.5对应的最优齿向动载系数为1.71左右，弯曲指数s＝3对应的齿向动载系数为kβ＝1.80左右，相比较而且弯曲指数s＝1.5对应的修形齿轮比弯曲指数s＝3对应的修形齿轮优化了5.3％。此外，注意到在负载越低的工况下，对应的动载系数也越大。从图中可以看出，此时采用较大的弯曲指数能够更好地降低齿向动载系数。结合图7所示结果可以分析出，在较低负载工况下，由于齿面受载弹性变形较小，采用较小的弯曲指数会使得载荷过于集中在齿面载荷分布中心的位置，导致齿向动载系数降低不如较大的弯曲指数明显。

由此可见，在不同多项式函数的弯曲指数下，都能够找到最优齿宽修形量，使得斜齿轮副的齿向动载系数最小。采用本发明提供的方法，不仅能够减缓动态载荷在齿宽方向分布不均的程度，降低动态载荷在整个齿宽方向的最大值，还能够改善齿宽方向的载荷分布中心，使得载荷中心位置逐渐靠近齿面中心，从而降低载荷中心位置不重合引起的侧偏摆力矩。在最优修形量下，当负载一定时，不同的弯曲指数下对应的修形齿轮均能够在整个工作转速范围内降低齿宽方向动态载荷。当齿宽修形量较大时，采用较大的弯曲指数会使得载荷中心位置附近的动载荷变化较为平缓，优于较小弯曲指数对应的修形齿轮；当齿宽修形量较小时，采用较小的弯曲指数会使得修形效果更佳。在负载较大时，由于齿面受载变形较大，此时采用较小弯曲指数的修形效果要由于较大的弯曲指数对应的修形齿轮；但在负载较小时，采用较小弯曲指数修形曲线会使得载荷分布过于集中，导致修形效果不如采用较大弯曲指数对应的修形齿轮。

实施例二

将上述切片后的薄片轮齿看作以接触点处的曲率半径ρ1,ρ2为半径的一对圆柱体的接触，当两个轴线平行的圆柱体在载荷的作用下相互接触并压紧时(如图11和12所示)，由于局部弹性变形，其接触线变成宽度为h的狭长接触带，由弹性力学理论可求得接触宽度h可表示为:

式中，fn为圆柱体所受法向压力，即薄片齿轮副所受啮合力fm,i；l为接触线长度，即处于啮合状态的薄片齿宽d/n；μ1和μ1为两圆柱体材料的泊松比；e1和e2为两圆柱体材料的弹性模量；ρ1和ρ2为两圆柱体的半径，即薄片齿轮副轮齿的瞬时半径。

两个齿轮在啮合挤压时，齿面接触区域所受压力大小相等，方向相反，因此齿面所受应力和应变均大小相等，方向相反，如图12所示。接触区域的表面产生局部应力称为接触应力，最大接触应力δh发生在变形最大的理论接触线上，可以表示为式所示:第i对薄片齿轮副最大接触应力的基本公式为:

根据本发明提供的啮合动力学模型计算流程和上述齿面接触动应力分析方法，首先，在输入转速为2000r/min，负载扭矩为500nm的稳态工况下，修形长度b＝d/2(即全齿宽修形)，多项式函数的弯曲指数s＝2.5的条件下，分别研究了不同齿宽修形量下第一齿轮的齿面动态接触应力分布状态。不同齿宽修形量下的齿面应力分布三维图和二维等高线图结果如图13-20所示。其中，齿宽最大修形量δd取值分别为[0μm,8μm,16μm,24μm]。从图13和14可以看出，在齿宽修形量δd＝0，即无修形的标准齿轮状态下，由于制造安装、轴承变形等误差使得齿面接触不均，导致出现齿面偏载现象。其中最大齿面应力出现在重合度较低的齿向一端位置，最大值约为419mpa。从二维等高线可以看出，无修形状态下的齿轮副齿面接触动应力在超过400mpa的齿面接触位置主要集中在齿面宽度为[-22.5mm，-10mm]的范围内。从图15-16可以看出，修形量δd＝8μm条件下，修形后使得齿宽应力较大的端面数值有所降低，且齿面上最大应力约为408mpa。从二维等高线可以看出，在该修形状态下的齿轮副齿面接触动应力在超过380mpa的齿面接触位置主要集中在齿面宽度为[-22.5mm，-3mm]的范围内。从图17-18可以看出，修形量δd＝16μm条件下，修形后使得齿面上最大应力约为379mpa。从二维等高线可以看出，在该修形状态下的齿轮副齿面接触动应力在超过360mpa的齿面接触位置主要集中在齿面宽度为[-19mm，3mm]的范围内。从图19-20可以看出，修形量δd＝24μm条件下，修形后使得齿面上最大应力约为368mpa。从二维等高线可以看出，在该修形状态下的齿轮副齿面接触动应力在超过350mpa的齿面接触位置主要集中在齿面宽度为[-15mm，5mm]的范围内。从结果可以得出，采用齿宽修形可以有效地消减齿端应力集中现象，降低齿面最大接触动应力。此外，齿宽修形还能减小载荷分布中心与齿面中心位置距离，缓解齿轮侧偏摆现象。

在输入转速为2000r/min，负载扭矩为500nm的稳态工况下，修形长度b＝d/2，齿宽修形量为δd＝24μm的条件下，不同弯曲指数下第一齿轮的齿面动态接触应力分布状态。不同弯曲指数下的齿面应力分布三维图和二维等高线图结果如图21-28所示。其中，多项式函数的弯曲指数s取值分别为[1.5,2,2.5,3]。从三维图中可以看出，无论采用哪种弯曲指数修形，在该修形量下都能显著降低齿宽端面接触应力集中现象，且使得齿面接触应力中心在齿面中心附近。此外，四种弯曲指数下的接触应力最大值均为412mpa左右。进一步对比四种弯曲指数下的接触应力二维等高线图，可以看出，当弯曲指数依次取值为[1.5,2,2.5,3]时，齿面接触应力超过400mpa的齿宽范围分别为[-4.5mm，3.5mm]，[-7mm，4mm]，[-12.5mm，5mm]，[-15mm，6mm]，接触应力峰值的齿宽跨度范围分别为8mm，11mm，17.5mm，21mm。可以看出随着修形指数的增大，该工况下的齿面接触应力峰值分布较为均匀。从分析结果得出，在输入工况和修形量一定的条件下，多项式函数的弯曲指数变化并不会明显改变齿面接触动应力的峰值及应力中心位置，但会影响接触动应力峰值附近的分布均匀状态。

需要说明的是，在本文中，诸如第一和第二等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。

对所公开的实施例的上述说明，使本领域专业技术人员能够实现或使用本发明。对实施例的多种修改对本领域的专业技术人员来说将是显而易见的，本文中所定义的一般原理可以在不脱离本发明的精神或范围的情况下，在其它实施例中实现。因此，本发明将不会被限制于本文所示的实施例，而是要符合与本文所公开的原理和创造特点相一致的最宽的范围。