一种隧道台阶法的判别方法与流程

本发明涉及隧道及地下工程技术领域，具体涉及一种隧道台阶法的判别方法。

背景技术：

隧道及地下工程施工时，具有多种施工方式，当工程建设条件较差或工程开挖高度过高时，采用一次性全断面开挖容易造成工程失稳，因此，在这种情况下常采用台阶法施工，以此确保工程施工安全，但现有技术中缺乏较准确的台阶法施工的判断方法，以确定台阶法施工的适用情况。

在台阶法施工中其核心内容就是明确各台阶科学合理的开挖高度，尤其是上台阶的开挖高度，上台阶开挖高度决定隧道是否存在坍塌危险，因此，需要找出台阶法施工中一次性开挖高度的临界值，一次性开挖高度在临界值范围内，可最大限度的保证隧道开挖的安全，目前，在实际工程中台阶法各高度的确定多采用工程类比法或技术人员的工程经验，缺乏系统地理论计算依据，无法较为准确的得出隧道一次性开挖高度。

因此，开发一种新隧道台阶法的判别方法，不但具有迫切的研究价值，也具有良好的经济效益和工业应用潜力，这正是本发明得以完成的动力所在和基础。

技术实现要素：

为了克服上述所指出的现有技术的缺陷，本发明人对此进行了深入研究，在付出了大量创造性劳动后，从而完成了本发明。

具体而言，本发明所要解决的技术问题是：提供一种隧道台阶法的判别方法，以解决现有隧道施工中台阶法施工缺乏系统地理论计算依据的技术问题。

为实现上述目的，本发明提供如下技术方案：

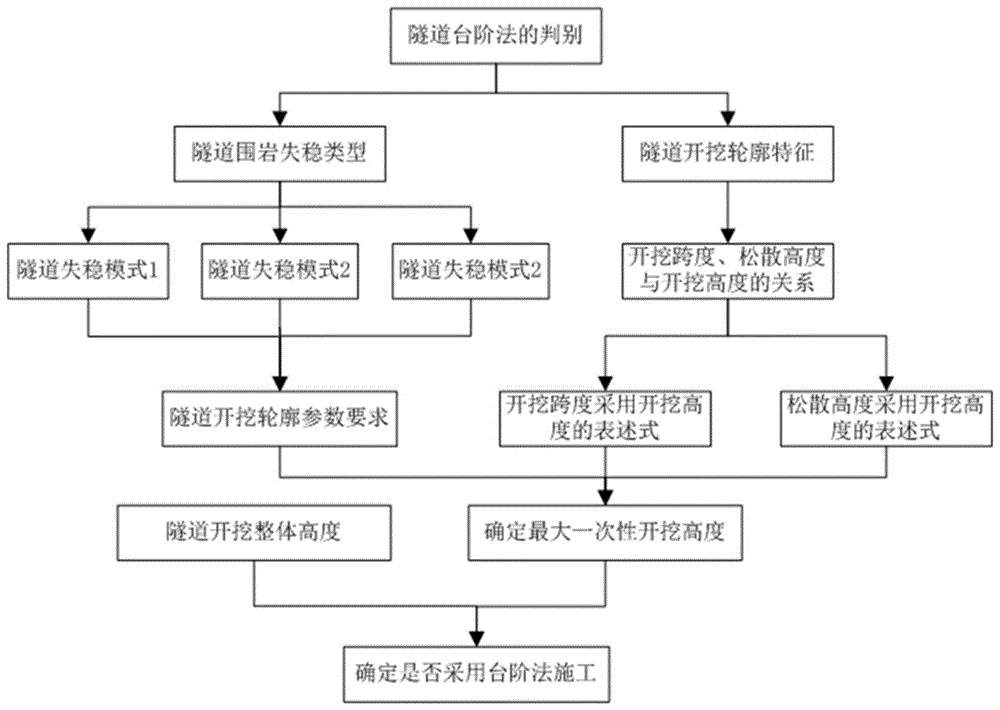
一种隧道台阶法的判别方法，该方法包括如下步骤：

(1)确定隧道的整体开挖高度；

(2)计算隧道一次性开挖高度的最大值；

(3)依据隧道整体开挖高度与最大一次性开挖高度两者间关系，确定隧道开挖是否采用台阶法。

在本发明中，作为一种改进，所述步骤(2)中隧道一次性开挖高度最大值的计算包括如下步骤：

1)以隧道的不同塌落类型建立不同的失稳模式；

2)以围岩稳定为控制条件建立失稳判别公式；

3)依据隧道开挖轮廓的几何特征，建立隧道开挖跨度、开挖高度及松散塌落高度间的关系；

4)利用隧道开挖跨度、开挖高度、松散塌落高度三者间的关系及失稳判别公式，计算得出失稳临界状态对应的隧道一次性开挖高度最大值。

在本发明中，作为一种改进，所述步骤(1)中塌落类型包括以下三种：

1)隧道拱顶围岩塌落失稳，表现为围岩受拉破坏，将其表述为失稳模式1；

2)隧道拱肩部位滑塌，表现为围岩在拱肩部位发生剪切破坏，将其表述为失稳模式2；

3)隧道边墙部位滑塌，表现为围岩边墙部位发生剪切滑移破坏，将其表述为失稳模式3。

在本发明中，作为一种改进，所述失稳模式1中隧道拱顶松散塌落，假定隧道顶部松散塌落范围为一简支梁，以隧道围岩梁弯拉为控制条件计算临界公式，梁内的最大弯矩发生在梁的中部，最大弯矩为：

式中：l为隧道开挖跨度；h为简支梁的厚度，即隧道围岩松散塌落高度；ρg为围岩重度；

根据材料力学中的相关理论，梁截面上的最大拉应力为：

稳定时最大拉应力应当小于围岩抗拉强度值，即最大拉应力应当满足：

σmax≤σt；

式中：σt为隧道围岩抗拉强度设计值；

即

得出失稳模式1的失稳判别公式为：

在本发明中，作为一种改进，所述失稳模式2中围岩梁自身较稳定，而在梁的两端存在软弱坍塌面，以围岩梁端潜在滑移面为控制条件计算临界公式，其中滑移面与水平面夹角为岩石滑移角α：其中：为岩石内摩擦角；

滑移面内塌落围岩梁的重力g：

g＝ρghl+ρgh²cotα；

斜面长为：

根据力学平衡关系得到作用在滑移面的力f分别为：

滑移面上的正应力为：

滑移面按照摩尔库伦准则为判据，所述摩尔库伦准则为：

式中：c为围岩粘聚力；

当τn≤τ，滑移面是稳定的，即：

在本发明中，作为一种改进，所述失稳模式3中隧道开挖产生的松散荷载作用于隧道两侧，造成隧道两侧围岩滑移，隧道两侧围岩滑移体上部承受的荷载为：

式中：h为隧道的开挖高度；

边墙三角体自身重量：

滑移面上的正应力为：

滑移面同样按照摩尔库伦准则为判据，可知：

当τn≤τ，滑移面是稳定的，即：

在本发明中，作为一种改进，隧道开挖轮廓采用弧形轮廓面，隧道开挖跨度l与开挖高度h用抛物线函数关系表述为：

l＝f(h)；

其中，f为对应的函数关系表达式；

隧道围岩松散塌落高度h取决于隧道开挖跨度l和高度h，可表述为：

h＝g(l，h)；

其中，g为对应的函数关系表达式；

由上述公式可得：

h＝g(f(h)，h)＝gf(h)。

在本发明中，作为一种改进，在隧道安全前提下，隧道围岩松散塌落高度h需满足三种失稳模式的临界公式，即：

由以上公式，计算得到隧道允许一次性开挖高度h的最大值hmax，若隧道整体开挖高度ha大于一次性开挖高度最大值hmax，采用台阶法进行施工。

与现有技术相比，本发明的有益效果是：

(1)本发明根据隧道施工中常见的塌方类型，给了三种隧道围岩塌方失稳模式和塌方失稳的理论判别公式，在此基础上，构建了隧道台阶法施工时台阶各尺寸与围岩稳定的关系，获取了台阶法上台阶一次开挖高度，为台阶法施工的工法设计提供了理论基础。

(2)通过确定一次性开挖高度与整体开挖高度之间的关系，从而判断是否采用台阶法施工，而一次性开挖高度的计算则结合隧道的参数，从而使该判断方法具有系统的理论数据支撑，保障隧道施工的安全可靠。

附图说明

为了更清楚地说明本发明具体实施方式或现有技术中的技术方案，下面将对具体实施方式或现有技术描述中所需要使用的附图作简单地介绍。在所有附图中，类似的元件或部分一般由类似的附图标记标识。附图中，各元件或部分并不一定按照实际的比例绘制。

图1为本发明的流程示意图；

图2为本发明实施例二中失稳模式1的结构示意图；

图3为本发明实施例二中失稳模式2的结构示意图；

图4为本发明实施例二中失稳模式3的结构示意图；

具体实施方式

下面将结合附图对本发明技术方案的实施例进行详细的描述。以下实施例仅用于更加清楚地说明本发明的技术方案，因此只作为示例，而不能以此来限制本发明的保护范围。

实施例一：如图1所示，一种隧道台阶法的判别方法，该方法包括如下步骤：

(1)确定隧道的整体开挖高度；

(2)计算隧道一次性开挖高度的最大值；

(3)依据隧道整体开挖高度与最大一次性开挖高度两者间关系，确定隧道开挖是否采用台阶法。

该方法利用一次性开挖高度与隧道的整体开挖高度之间的关系进行判别，其中，若隧道整体开挖高度ha大于隧道允许一次性开挖高度的最大值hmax，应采用台阶法进行施工，若隧道整体开挖高度ha小于隧道允许一次性开挖高度的最大值hmax，则可以采用全断面开挖施工，所述隧道的整体开挖高度ha和开挖跨度l为施工前即可确定的参数。

其中，隧道一次性开挖高度最大值的计算包括如下步骤：

1)以隧道的不同塌落类型建立不同的失稳模式；

2)以围岩稳定为控制条件建立失稳判别公式；

3)依据隧道开挖轮廓的几何特征，建立隧道开挖跨度、开挖高度及松散塌落高度间的关系；

4)利用隧道开挖跨度、开挖高度、松散塌落高度三者间的关系及失稳判别公式，计算得出失稳临界状态对应的隧道一次性开挖高度最大值。

依据隧道施工中围岩塌方类型建立三种隧道围岩失稳模式，失稳模式1为隧道拱顶围岩塌落失稳，该模式表现为围岩受拉破坏；失稳模式2为隧道拱肩部位滑塌，该模式表现为围岩在拱肩部位发生剪切破坏；失稳模式3为隧道边墙部位滑塌，该模式表现为围岩边墙部位发生剪切滑移破坏。

隧道一次性开挖高度需要满足三种失稳模式，其高度范围在失稳判别公式内，才能保证隧道围岩的稳定性。

其中，所述失稳模式1中隧道拱顶松散塌落，假定隧道顶部松散塌落范围为一简支梁，以隧道围岩梁弯拉为控制条件，梁内的最大弯矩发生在梁的中部，最大弯矩为：

式中：l为隧道开挖跨度；h为简支梁的厚度，即隧道围岩松散塌落高度；ρg为围岩重度；

根据材料力学中的相关理论，梁截面上的最大拉应力为：

稳定时最大拉应力应当小于围岩抗拉强度值，即最大拉应力应当满足：

σmax≤σt；

式中：σt为隧道围岩抗拉强度设计值；

即：

得出失稳模式1的失稳判别公式为：

所述失稳模式2中围岩梁自身较稳定，而在梁的两端存在软弱坍塌面，以围岩梁端潜在滑移面为控制条件计算临界公式，其中滑移面与水平面夹角为岩石滑移角α：其中：为岩石内摩擦角；

滑移面内塌落围岩梁的重力g：

g＝ρghl+ρgh²cotα；

斜面长为：

根据力学平衡关系得到作用在滑移面的力f分别为：

滑移面上的正应力为：

滑移面按照摩尔库伦准则为判据，所述摩尔库伦准则为：

式中：c为围岩粘聚力；

当τn≤τ，滑移面是稳定的，即：

所述失稳模式3中隧道开挖产生的松散荷载作用于隧道两侧，造成隧道两侧围岩滑移，隧道两侧围岩滑移体上部承受的荷载为：

式中：h为隧道的开挖高度；

边墙三角体自身重量：

滑移面上的正应力为：

滑移面同样按照摩尔库伦准则为判据，可知：

当τn≤τ，滑移面是稳定的，即：

经过计算，得出失稳模式1、失稳模式2和失稳模式3的失稳判别公式分别为：

隧道的开挖轮廓具有多种，其中，最常见的为弧形轮廓面，弧形轮廓面的计算公式可采用抛物线函数关系，隧道开挖跨度l与开挖高度h用抛物线函数关系表述为：

l＝f(h)；

其中，f为对应不同轮廓面的函数关系表达式；

隧道围岩松散塌落高度h取决于隧道开挖跨度l和高度h，可表述为：

h＝g(l，h)；

其中，g同样为对应的函数关系表达式；

由上述公式可得：

h＝g(f(h)，h)＝gf(h)。

在隧道安全前提下，隧道围岩松散塌落高度h需满足三种失稳模式的临界公式，即：

将已知的简支梁的厚度h与l带入公式，通过计算可得到隧道允许一次性开挖高度h的最大临界值hmax，若隧道整体开挖高度ha大于一次性开挖高度最大值hmax，采用台阶法进行施工。

实施例二：实施例二与实施例一基本相同，其不同之处在于：如图2所示，隧道采用台阶开挖时，假定隧道顶部松散塌落范围为一简支梁(abcd)，依据简支梁结构力学计算结果，梁内的最大弯矩发生在梁的中部，最大弯矩为：

式中：l为隧道开挖跨度；h为简支梁(abcd)的厚度；围岩重度为ρg。

根据材料力学中的相关理论，梁截面上的最大拉应力为：

稳定时最大拉应力应当小于围岩抗拉强度值，即最大拉应力应当满足：

σmax≤σt；

式中：σt为隧道围岩抗拉强度设计值。

即：

如图3所示，隧道开挖时，隧道塌落围岩梁(拱)abcd自身较稳定，而在梁的两端存在一定的软弱面，假定该软弱滑移面分别为eg、fh，其中滑移面与水平面夹角为岩石滑移角，值为为岩石内摩擦角，为计算方面和考虑安全性，计算中假定滑移面仅为ec和fd，则滑移面内塌落围岩梁(拱)efcd的重力g：

g＝ρghl+ρgh²cotα；

斜面长为：

根据力学平衡关系得到作用在滑移面的力f分别为：

由以上三者关系可得滑移面上的正应力为：

滑移面上的按照摩尔库伦准则为判据：

若：τn≤τ，是稳定的；否则，沿滑移面破坏，即：

如图4所示，隧道采用台阶开挖时，假定开挖后的塌方以边墙滑移，图中cbg、efh为主，隧道开挖产生的松散荷载作用于隧道两侧的cbg、efh上，造成隧道两侧围岩沿cg和fh面滑移，隧道两侧滑移体bcg或efh上部abcf承受的荷载为：

边墙三角体自身重量：

滑移面上的正应力为：

滑移面上的按照摩尔库伦准则为判据，可知：

若：τn≤τ，是稳定的；否则，沿滑移面破坏，即：

实施例三：隧道为v级围岩隧道，隧道围岩的已知力学参数取值如下：

ρg(围岩重度)＝20kn/m³；

c(围岩粘聚力)＝0.1mpa；

σt(隧道围岩抗拉强度设计值)＝0.12mpa。

隧道的开挖轮廓为椭圆形断面，隧道整体开挖高度为10m，开挖跨度为6m，其椭圆形断面的开挖轮廓函数表述为：

角度的函数式为：

sinα＝sin57°＝0.838；

cosα＝cos57°＝0.544；

cotα＝cot57°＝0.649。

具体计算过程包括如下四个步骤：

(1)若隧道开挖安全，需隧道开挖轮廓各参数需满足三种隧道失稳模式关系：

将隧道的具体参数带入后，即：

0.5l+0.32h≤10；

(2)根据隧道开挖轮廓参数的特征，可知：

则：

此l与h的关系式对应实施例一中的l＝f(h)关系式。

根据公路隧道设计规范，开挖诱发的潜在松散塌落高度h其值为：

h＝0.45×2^s-1ω；

式中：s为围岩级别v级；ω为宽度影响系数；

此关系式对应实施例一中的h＝g(l，h)关系式。

式中ω＝1+i(l-5)，当l＜5m时，取i＝0.2，l≥5m时，取i＝0.1。

由此可知：

当l＜5m时：

h＝3.6·(1+0.2(l-5))；

h＝3.6·(1+0.1(l-5))；

由此推得，当h＜2.24或h＞7.76，则：

当7.76≥h≥2.24，则：；

(3)确定h的最大值：

首先考虑h＝2.24m的情况，即h＝2.24m、h＝3.6m、l＝5.0m，核查是否满足三种失稳模式下的安全要求：

0.5l+0.32h＝2.5+1.12＝3.62＜10

计算后满足安全要求。

考虑h＝5m的情况，即h＝5m、h＝3.96m、l＝6.0m，核查是否满足三种失稳模式下的安全要求：

0.5l+0.32h＝4.26＜10；

计算后不满足隧道失稳模式1要求，表明该算例中控制隧道围岩稳定的是隧道失稳模式1，由隧道失稳模式1可知，其极限情况为：

即：

求得：h＝3m；l＝5.5m，h＝3.78m。

(4)隧道施工台阶法确定：

由上述计算得知，隧道整体开挖高度为10m时，隧道一次性最大开挖安全高度为3m，隧道一次性最大开挖高度小于隧道整体开挖高度，因此，隧道应采用台阶法施工。

最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的范围，其均应涵盖在本发明的权利要求和说明书的范围当中。