一种考虑雾化和邻近效应的超大规模集成电路布局方法与流程

本发明属于超大规模集成电路设计技术领域，具体涉及一种考虑雾化和邻近效应的超大规模集成电路布局方法。

背景技术：

由于ebl可以打印出精细的图案，它被用于亚22nm工艺节点和以上的图案。电子枪通过一组透镜和光圈直接发射电子在晶片上刻下图案。当电子枪发射出的一次电子束击中电阻和衬底时，电子可能会散射。散射电子产生后向散射电子，后向散射电子可能击中物镜的底部。因此，撞击可能产生下一代电子，即所谓的重新散射电子。这些散射的、反散射的和重新散射的电子可能会引起不希望的曝光，从而导致邻近效应和雾化效应。

邻近效应是由散射和反散射电子产生的。更准确地说，散射电子(前向散射电子)引起前向邻近效应，即电子在进入光刻胶和衬底时发生小角度偏转。相反，后向散射电子(称为后向散射电子)会产生后向邻近效应，这种效应通常在较大的角度下发生偏转。此外，反散射电子可能会离开电阻，撞击物镜底部，再次反弹到电阻中，从而产生重新散射的电子。重新散射的电子被分散到离主曝光点几毫米远的地方。这些重新散射的电子会引起过度曝光，从而造成布局模式的变化，称为雾化效应。

一些已发表的论文解决了关键的雾化和邻近效应，但他们大多数处理这两个影响在制造过程或后布局阶段。shimomura等人通过添加散射电子吸收板来处理雾化效应。hudek和bayer利用一系列实验数据来确定邻近效应的最优参数，开发了一个软件工具(称为“prox-in”)来确定一个最优的控制点扩展函数来修正邻近效应。然而，布局后修正非常耗时。除了运行时间较长外，为了保证关键维度的精度，需要位图的海量数据。

为了更早地解决雾化效应，huang和chang提出了第一个芯片级布局算法，以最小化芯片上的雾化变化。其基本思想是在雾化模型的指导下布局区间，以最小化布局过程中的雾化变化。雾化模型是一种利用快速高斯变换来估计雾化效应的精确评价方案。实验结果表明，他们的方法达到了高解决率。然而，这项工作没有考虑关键的邻近效应。另一个问题是，与不考虑雾化效应的布局方法相比，其运行时间长了2.44倍。因此，需要设计一种有效的算法来同时处理关键的雾化效应和接近效应。

技术实现要素：

本发明的目的在于提供一种考虑雾化和邻近效应的超大规模集成电路布局方法，该方法有利于减少雾化和邻近效应带来的不良影响，提升布局效率。

为实现上述目的，本发明采用的技术方案是：一种考虑雾化和邻近效应的超大规模集成电路布局方法，包括如下步骤：

(1)对电子束光刻ebl中雾化和邻近效应建立能量分布模型并描述其变化；

(2)优化全局布局中的模型与函数，确定平滑的目标函数f(x，y)；

(3)引入新变量将无约束最小化问题化为具有线性约束的可分离最小化问题csmp；

(4)确定可分离最小化问题的邻近组admm算法与迭代式；

(5)解决邻近组迭代中的两个子问题；

(6)对邻近组admm算法进行收敛性分析。

进一步地，所述步骤(1)中，在ebl中，将雾化效应和接近效应分别建模为高斯分布和双高斯函数，ffog(d)雾化效应和邻近效应fpro(d)的数学模型分别为：

其中，是距入射点的距离，βf、βf和βb是雾化效应作用范围、前向邻近效应和后向邻近效应；vf是与雾化效应的权重有关的参数；η是后向散射能量与前向能量之比；

对于雾化效应，给定评估点ti和受该点影响的一组源通过快速高斯变换计算评估方案为：

其中，qj是aj的权重，δa是正常数；同样，前向邻近效应和后向邻近效应由下式计算：

式中，和是由正向和反向引起的发生源集，分别在评估点ti处具有近似效果；

采用上述评估方案来估算fpe：设评估点为它们均匀分布在整个布局上，雾化效应的变化由下式计算：

邻近效应的变化由下式计算：

其中，x和y是发生源的x和y坐标。

进一步地，所述步骤(2)中，在全局布局中，线长和密度函数都不平滑，用对数和线长模型和钟形函数分别近似总半周长线长和平滑密度函数；将全局布局问题公式化为平滑约束最小化问题，如下所示：

其中，mb为binb中可移动单元的最大允许面积；

为了优化雾化和邻近效应的变化，同时保持良好的布局线长度和密度，将布局的目标函数定义为：

其中，λ1、λ2、λ3和λ4为权重，该些权重不断更新，以在迭代过程中搜索所有电路单元的最佳位置；

通过引入两个新变量(g，h)，将无约束最小化问题进一步公式化为具有线性约束的可分离最小化问题，如下所示：

其中，表示线长和密度约束，θ2(g，h)＝λ3sf(g，h)+λ4sp(q，h)表示雾化和邻近变化；该公式将雾化和邻近变化与线长和密度约束分开。

进一步地，所述步骤(3)中，与式(5)的最小化问题相关的拉格朗日函数为：

其中，增广拉格朗日乘子法为：

采用近端组admm来解决式(5)的最小化问题：给定基于增强的拉格朗日函数(6)，通过以下公式，式(5)的最小化问题的近端组admm产生下一个迭代

式中，和是近似项；该方法将原始变量分为(x，y)和(g，h)两类，然后采用近端admm解决两个求解问题；在近端组admm的每次迭代中，有两个子问题要解决，分别是式(7)的子问题和式(8)的子问题；

对于式(7)的子问题，使用最速下降法来最小化线长和密度约束违规；根据最优性的一阶必要条件，从式(7)得出：

以及

这导致以下形式的最陡下降步骤：

令：

和

式(8)的子问题相当于minφ(g)和的一阶最优性条件，有和

以同样的方式计算梯度和

首先，有：

式(12)的计算，即：

由于雾化和邻近效应都是相关高斯分布函数的总和，因此通过相同的方法获得sf(g，h^t)和sp(g，h^t)的偏导数；sf(g，h^t)的偏导数描述为：

如上将平均数分成两部分：一个是主要受雾化效应影响的部分，另一个是主要不受雾化效应影响的部分的平均值；由于平均值主要不受雾化效应的影响，将其视为常数，并表示为e，即选择周围的网格来计算平均效果变化值；然后，有：

其中，是评估点ti的坐标；

将受评估点ti影响的窗口表示为γ；使用积分法近似指数函数，得到：

其中，wγ、hγ和rγ分别是窗口γ的宽度、高度和边界；ti是一个评估点，ai位于其影响区域；

为了估计式(15)中的的值，采用确界原理，有：

将式(16)、(17)和(18)代入(15)，得到：

并且，

遵循式(14)～(20)的过程，计算出：

结合式(12)、(13)、(19)和(21)，并让得到：

即：

同样，得到：

相较于现有技术，本发明具有以下有益效果：1)本发明将降低雾化和邻近效应影响的全局布局问题表述为一个可分离的线性约束最小化问题，这大大降低了寻优问题的复杂性。2、本发明提出了一个新的邻近组admm算法来解决可分离极小化问题。为了利用可分重公式的优点，在该方法的每次迭代中，以较低的计算代价解决了两个子问题。3)本发明在两个可靠的假设下，保证了对一阶临界点的全局收敛性，为生成的解的质量提供了理论保证。4、本发明可以高效的解决考虑雾化和邻近效应的vlsi布局问题。经实验结果表明，本发明方法对于所解决的问题是有效和高效的。与目前最先进的算法相比，本方法不仅降低了13.4％的雾化效应和21.4％的邻近效应带来的影响，而且还有1.65倍加速。

附图说明

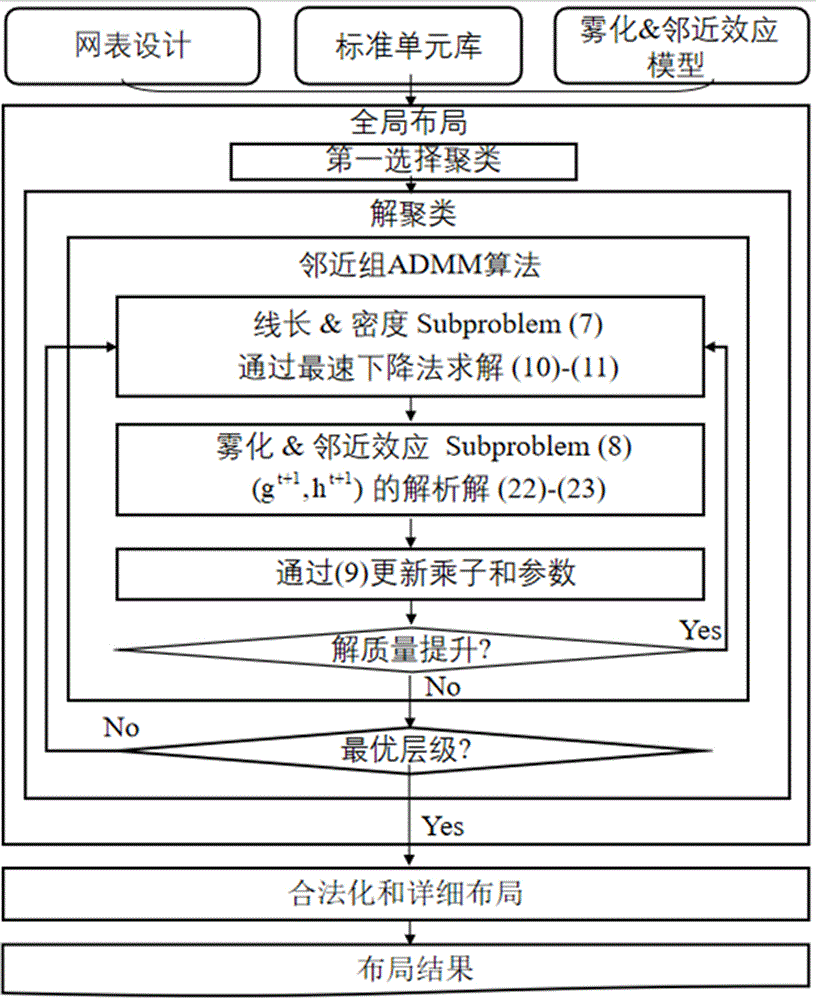
图1是本发明实施例的方法实现流程图。

具体实施方式

下面结合附图及具体实施例对本发明作进一步说明。

本发明提供了一种考虑雾化和邻近效应的超大规模集成电路布局方法，来解决考虑雾化和邻近效应的vlsi布局问题，进而减少雾化和邻近效应带来的不良影响，从而提升布局效率。该方法的基本思想是先将全局布局问题表述为一个可分离的线性约束最小化问题。根据雾化和邻近效应的能量模型，将其中的目标通过交替的方式一个一个解决，写出邻近组并求解，也大大降低了寻优问题的复杂性，同时降低了计算代价，从而高效地降低了雾化和邻近效应带来的影响。在该方法的每次迭代中，以较低的计算代价解决了两个子问题。第一个子问题(主要与线长和密度有关)通过无线搜索的最速下降算法求解，而第二个子问题(主要与雾化和邻近效应有关)通过一些近似技术用解析解近似求解。该方法具体包括如下步骤：

(1)对电子束光刻(ebl)中雾化和邻近效应建立能量分布模型并描述其变化。

(2)优化全局布局中的模型与函数，确定平滑的目标函数f(x，y)。

(3)引入新变量将无约束最小化问题化为具有线性约束的可分离最小化问题(csmp)。

(4)确定可分离最小化问题的邻近组admm算法与迭代式。

(5)解决邻近组迭代中的两个子问题。

(6)对邻近组admm算法进行收敛性分析。

请参见图1，图1是本发明方法的实现流程图。该方法的数学模型描述如下：

在ebl中，将雾化效应和接近效应分别建模为高斯分布和双高斯函数，ffog(d)雾化效应和邻近效应fpro(d)的数学模型分别为：

其中，是距入射点的距离，βf、βf和βb是雾化效应作用范围、前向邻近效应和后向邻近效应。vf是与雾化效应的权重有关的参数。η是后向散射能量与前向能量之比。对于可校正的最小尺寸，βf为20000μm，βf为0.06μm，βb为30μm。本发明提出了一种有效且准确的评估方案，以通过快速高斯变换来估计雾化效应。在该方案中，每个标准单元都被视为发生源，并且选择均匀分布在整个布局上的评估点来估计两种效果的变化(两个相邻评估点之间的间距是一个常数，例如5μm)。

对于雾化效应，给定评估点ti和受该点影响的一组源通过快速高斯变换计算评估方案为：

其中，qj是aj的权重，δa是正常数。同样，前向邻近效应和后向邻近效应由下式计算：

式中，和是由正向和反向引起的发生源集，分别在评估点ti处具有近似效果。

在本发明中，采用上述高效、准确的评估方案来估算fpe：设评估点为它们均匀分布在整个布局上，雾化效应的变化由下式计算：

邻近效应的变化由下式计算：

其中，x和y是发生源的x和y坐标，例如标准单元格的位置。

在全局布局中，线长和密度函数都不平滑，用对数和线长模型和钟形函数分别近似总半周长线长(hpwl)和平滑密度函数。将全局布局问题公式化为平滑约束最小化问题，如下所示：

其中，mb为binb中可移动单元的最大允许面积。

为了优化雾化和邻近效应的变化，同时保持良好的布局线长度和密度，将布局的目标函数定义为：

其中，λ1、λ2、λ3和λ4为权重，该些权重不断更新，以在迭代过程中搜索所有电路单元的最佳位置。

通过引入两个新变量(g，h)，将无约束最小化问题进一步公式化为具有线性约束的可分离最小化问题，如下所示：

其中，表示线长和密度约束，θ2(g，h)＝λ3sf(g，h)+λ4sp(q，h)表示雾化和邻近变化。该公式将雾化和邻近变化与线长和密度约束分开。特别地，两个目标函数可以以交替的方式一个一个地优化，这可以显着加快优化过程。

admm算法是一种针对可分离结构的优化问题的有效算法，尤其是对于具有线性约束的可分离优化问题。本发明进一步提出了一种新颖的近端组admm来解决式(5)的最小化问题，并证明该方法生成的迭代序列收敛于式(5)的最小化问题的一阶临界点。

图1中“proximalgroupadmm”部分具体如下：

所述步骤(3)中，与式(5)的最小化问题相关的拉格朗日函数为：

其中，增广拉格朗日乘子法为：

采用近端组admm来解决式(5)的最小化问题：给定基于增强的拉格朗日函数(6)，通过以下公式，式(5)的最小化问题的近端组admm产生下一个迭代

式中，和是近似项。该方法将原始变量分为(x，y)和(g，h)两类，然后采用近端admm解决两个求解问题。在近端组admm的每次迭代中，有两个子问题要解决，分别是式(7)的子问题和式(8)的子问题。

图1中“wirelength&densitysubproblem(7)；solve(10)(11)bysteepestdescentmethod”部分，具体方式如下：

对于式(7)的子问题，使用最速下降法来最小化线长和密度约束违规。根据最优性的一阶必要条件，从式(7)得出：

以及

这导致以下形式的最陡下降步骤：

图1中“fogging&proximityeffectssubproblem(8)；analyticalsolutionofvia(22)-(23)”部分，具体方式如下：

令：

和

式(8)的子问题相当于minφ(g)和的一阶最优性条件，有和

以同样的方式计算梯度和

首先，有：

式(12)的计算，即：

由于雾化和邻近效应都是相关高斯分布函数的总和，因此通过相同的方法获得sf(g，h^t)和sp(g，h^t)的偏导数。sf(g，h^t)的偏导数描述为：

如上将平均数分成两部分：一个是主要受雾化效应影响的部分，另一个是主要不受雾化效应影响的部分的平均值。由于平均值主要不受雾化效应的影响，将其视为常数，并表示为e，即选择周围的网格来计算平均效果变化值。然后，有：

其由是评估点ti的坐标。之所以成立最后一个等式，是因为独立于gi。

将受评估点ti影响的窗口表示为γ。使用积分法近似指数函数，得到：

其中，wγ、hγ和rγ分别是窗口γ的宽度、高度和边界。ti是一个评估点，ai位于其影响区域。

为了估计式(15)中的的值，采用确界原理，有：

将式(16)、(17)和(18)代入(15)，得到：

并且，

遵循式(14)～(20)的过程，计算出：

这里q可以用类似的方法推导出来。结合式(12)、(13)、(19)和(21)，并让得到：

即：

同样，得到：

图1中“legalization&detailedplacement；placementresult”部分，具体方式如下：

对于每个非法单元，找最近且合法的位置来放置该单元。

所述步骤(5)中，通过一阶最优条件，问题(5)的临界点满足以下这一方程：

通过之前提出的邻近组admm算法(交替方向乘子法)，得到方程：

做如下假设：1)la在所考虑的芯片区域内位于下面。2)和在(x，y)上是lipschitz连续的，而和在(g，h)上是lipschitz连续的。表示然后我们有以下引理：

引理1)假设序列{z^t}是通过提出的方法生成的。然后，如果惩罚参数β＞0和γ＞0足够大，则函数值的序列将单调递减，其中，只要la有下界，我们就能得到方程：

和

定理1)由邻近的admm组生成{zt}，则它收敛到问题的临界点。

证明：通过引理1，h0是一个有界闭集的地方。因此，{z^t}是收敛的，至少有一个收敛的子序列。假设是一个收敛的子序列，和ti→+∞。

由式(25)-(30)和式(31)-(32)可得：

和

同理，可得：

和

注意，对于任意t大于等于1，ti属于自然数，以上所有方程成立，对方程(25)-(30)两边同时对ti取极限，并且，注意到当ti趋于0时趋于z，我们就有极限点z满足条件24，因此它是问题(5)的驻点。

以上是本发明的较佳实施例，凡依本发明技术方案所作的改变，所产生的功能作用未超出本发明技术方案的范围时，均属于本发明的保护范围。