一种高效的汽车侧面碰撞安全可靠性设计优化方法与流程

本发明涉及汽车可靠性设计优化
技术领域：
，尤其涉及一种高效的汽车侧面碰撞安全可靠性设计优化方法。
背景技术：
：随着高性能计算机的出现，汽车行业已经使用多学科的优化和耐撞性仿真解决车辆侧面碰撞的安全问题，从而减少新车辆开发的成本和时间。但是，基于仿真的优化通常是确定性的优化设计，这些设计通常采用设计约束边界的极限。实际工程中，汽车整车结构中存在材料属性、几何特性、碰撞环境等大量不确定因素，直接影响车辆侧面碰撞的可靠性。基于可靠性的设计优化(rbdo)既可以获得最佳的设计方案，同时充分考虑这些不确定性因素的影响，能够有效平衡最佳设计目标和可靠性。rbdo已经成为解决工程设计中复杂问题的最强大方法之一，并且发展出许多高级理论和方法。传统的rbdo解决方法通常分为三类。(1)双循环方法。这类方法可靠性分析嵌套在设计优化内部，每次通过优化算法迭代设计空间中的新点时，都需要执行可靠性分析。双循环方法效率很低，无法满足工程应用的要求。(2)单循环方法。这类方法的采用近似技术或karush-kuhn-tucker(kkt)最优性条件代替可靠性分析，从而将嵌套双循环转化为单循环问题。它计算效率非常高，但是当功能函数的非线性程度较高时可能不收敛。(3)序列优化方法。这类方法使可靠性分析与设计优化解耦，两者顺序执行直到收敛。序列优化方法是最有效的rbdo方法之一，具有精度高、精度高和稳定性强的特点。上述传统的rbdo求解方法基本采用一阶可靠性分析方法，需要迭代计算mpp点，在处理具有高维和高度非线性问题时，可能会导致效率降低或者精度不足。考虑到汽车侧面碰撞问题具有复杂度高、工况(环境)极端、非线性程度高等特点，传统的方法无法有效解决这个问题。上述方法也无法集成许多先进的可靠性分析方法，如降维积分方法(drm)，稀疏网格积分(sgi)等。与基于mpp的可靠性分析方法相比，这些方法无需计算功能函数的导数，不要执行迭代求解过程，并且在某些情况下计算效率更高。如果将这些先进的方法集成到序列优化方法中，有希望开发出高效、高精度的rbdo求解方法，对于汽车侧面碰撞可靠性优化设计问题的研究具有较大的意义。如中国专利公告号cn104036100b，授权公告日20170510，公开了一种不确定性下基于贝叶斯偏差修正的汽车可靠性设计优化方法，属于汽车可靠性设计优化
技术领域：
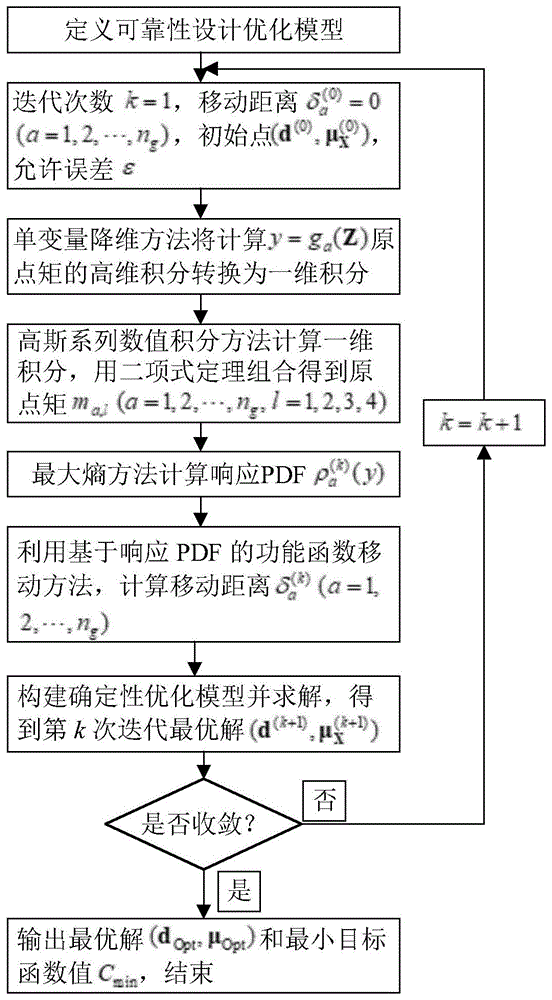
。该方法包括以下步骤：步骤一：定义基于可靠性设计优化(rbdo)问题；步骤二：为贝叶斯推理偏差模型以及初始响应面模型构建试验设计(doe)矩阵；步骤三：使用步骤二中所述的偏差模型修正初始响应面模型并量化来自于重复试验和cae仿真的不确定性；步骤四：运行rbdo优化程序寻最优、最可靠解；步骤五：进行蒙特卡洛仿真(mcs)验证所得解的可靠性。该方法运算次数多，耗时长，效率低。技术实现要素：本发明要解决的技术问题是当完成优化目标的条件下，例如优化目标设为在保证侧面碰撞的性能前提下最小化整车重量，进一步地减少运算次数，在保持更高精度的情况下，节省优化设计时间，提高优化设计效率。为解决上述问题而采用了一种高性能的汽车碰撞安全可靠性设计优化方法该方法的可靠性分析和确定性优化按顺序执行，先用单变量降维方法求出响应的前四阶矩，并根据最大熵原理求出响应的pdf。然后进行确定性优化，利用基于响应pdf的功能函数移动方法求出平移距离，构造等效的确定性优化模型并求解，得到新的最优解。以新的最优解作为输入，重复执行可靠性分析和确定性优化过程，直至满足收敛条件，最终得到原优化模型的最优解。具体步骤如下：第一步：根据汽车侧面碰撞安全性的可靠性设计优化的要求，定义数学优化模型，定义数学优化模型包括确定系统的确定性设计变量、随机设计变量和随机参数，根据随机变量、参数的概率统计特点获得概率分布；同时要确定目标函数，建立系统功能函数，设置目标可靠度；第二步：设定迭代次数k＝1，功能函数pdf的移动距离初始点设置允许误差ε(一个较小的正数)，令a＝1来记录功能函数编号；第三步：引入单变量降维方法，将系功能函数分解为单个随机参量的子系统，用于使计算响应原点矩的高维积分转换为计算一维积分qij；第四步：利用高斯系列数值积分方法计算一维积分qij，用二项式定理组合qij计算原点矩ma,l。第五步：假设待估响应y的概率密度函数为使用最大熵方法求取得到ρa(y)的解析式，在得到响应y的pdfρ(y)后，通过对ρ(y)进行积分来计算约束的可靠度ra；第六步：令a＝a+1，重复第三～五步，直至求出所有功能函数响应的概率密度函数ρa和可靠度ra(a＝1,2,…,ng)；第七步：利用基于响应pdf的功能函数移动方法，计算移动距离第八步：构建确定性优化模型并求解，得到第k次迭代的最优解和最小目标函数值第九步：判断是否成立，若成立执行第十步；若不成立，令k＝k+1，a＝1，重复第三～九歩。第十步：输出最优解和最小目标函数值结束。作为本发明进一步的改进，在第一步中，可靠性设计优化的数学模型为：其中，c(d,μx)是目标函数，p{ga(d,x,p)≥0}是第a个功能函数的可靠度，ga(d,x,p)是第a个功能函数，d是确定性设计变量，x是随机设计变量，p是随机参数，μx,μp分别是x,p均值，是目标可靠度，dl,du,是确定性设计变量d和随机设计变量x各自均值的上下界，用z＝(x,p)代表所有的随机变量/参数，则ga(d,x,p)简写为ga(d,z)；由于进行不确定性分析时，d不变，因此可将ga(d,z)简写为ga(z)。作为本发明进一步的改进，在第一步中，当优化目标为在保证侧面碰撞的性能前提下最小化整车重量时，采用欧洲增强型车辆安全委员会的侧面碰撞测试标准，则可靠性设计优化的数学模型为：s.t.p(腹部载荷：fabdom≤1.0kn)≥rtp(肋变形(上/中/下)：defrib_l/rib_m/rib_u≤32mm)≥rtp(粘性标准(上/中/下)：vcupper/middle/lower≤0.32m/s)≥rtp(耻骨综合力：forcepubic≤4.0kn)≥rtp(b柱中点速度：velb-pillar≤9.9mm/ms)≥rtp(前门处的b柱速度：veldoor≤15.7mm/ms)≥rt作为本发明进一步的改进，采用最佳拉丁超立方体抽样和二次反向逐步回归建立包括weight、fabdom、defrib_l、defrib_m、defrib_u、vcupper、vcmiddle、vclower、forcepubic、velb-pillar和veldoor的全局响应面模型。此外，在上述技术方案中，所述随机设计变量x包括x1：b柱内壁厚度、x2：b柱加固的厚度、x3：地板侧面内壁的厚度、x4：横梁的厚度、x5：车门梁的厚度、x6：门带线加固厚度、x7：车顶纵梁的厚度、x8：b柱内壁材料和x9：地板侧面内壁材料；所述随机参数p包括x10：移动壁障高度和x11:撞击位置。作为本发明进一步的改进，所述第三步的具体步骤为：计算第a个功能函数ga(z)的前l阶原点矩ma,l，l＝1,2,3,4表达式为：式中e{·}代表数学期望算子；对功能函数y＝ga(z)进行加性分解：式中μi表示随机变量zi的均值，n表示随机变量个数；使用单变量降维方法后响应y的第l阶原点矩公式：将式(4)使用二项式定理展开得到：作以下定义：则式(4)可简化成：上式的可通过下列递归公式求出：通过式(3)～(8)，可以将高维积分转化为求解数学期望这是一个一维积分；为方便描述，用qij表示该积分，则有：式中是zi的概率密度函数。作为本发明进一步的改进，所述第四步的具体步骤为：高斯系列数值积分公式为：式中ωi,m代表权重，vi,h代表积分节点，m代表积分节点数目。由高斯系列数值积分计算所有的qij，结合式(7)～(8)，即可求出原点矩ma,l，每个一维积分使用m个积分节点，对于n维功能函数，所需积分节点的数目为m×n+1，即需要计算m×n+1次功能函数。作为本发明进一步的改进，所述第五步的具体步骤为：假设待估响应y的概率密度函数为则其山农熵计算公式为：使用最大熵方法(mem)求取可描述为以下优化问题：使用拉格朗日乘子法求解，构造拉格朗日函数如下：当拉格朗日函数对于概率密度函数的偏导数等于0时，式(9)取得极值，从而得到ρa(y)的解析式如下：求出拉格朗日乘子λl(l＝0,1,2,3,4)并得到响应y的pdfρ(y)后，可以通过对ρ(y)进行积分来计算约束的可靠度ra：作为本发明进一步的改进，所述第七步的具体步骤为：将可靠性优化模型改写为：式中，代表第a个功能函数响应的pdf，对于优化过程中的每一组试探点(d,μx)，都可以用第三～五步求出响应的pdf，因此是设计变量的函数，可以表示为基于响应pdf的功能函数移动方法的基本思想为：通常，可靠性设计中的可靠性要求(≥0.90)通常远高于确定性设计所实现的可靠性(≈0.5)，即概率约束比确定性约束更严格。在几何上，当目标可靠度rt＞0.5时，概率设计优化的可行域比确定性优化的可行域窄。建立等效确定性优化模型的关键在于从概率约束到确定性约束的转换，需要计算从确定性约束边界到概率约束边界的平移距离。通过平移，将实际的约束边界从确定性约束边界移向概率约束边界，从而提高该约束的可靠度。假设和分别是第k次和第(k+1)次迭代得到的响应的pdf，代表第k次的最优点，(d,μx)代表第(k+1)次迭代的试探点；第k次和第k+1次迭代响应的pdf的关系为：式中，代表设计变量从变为(d,μx)时ρa(y|d,μx)的移动距离，这个距离等于功能函数值之差：为了保证满足概率约束，需要当前迭代步的约束可靠度大于或等于目标可靠度：将式(17)代入式(19)，得到：因为在第k次迭代时表达式已经求出，所以式(20)不等号左边项的大小只与的取值有关，可以定义为的函数：式(20)可以改写为：通过求解上面的方程，可以获得平移距离式中arch表示函数h的逆函数，将式(18)代入式(23)得到：考虑到确定性优化约束与概率约束的不等符号相同，式(24)可以取等号，最终得到平移距离的公式为：作为本发明进一步的改进，所述第八步的具体步骤为：第k次迭代确定性优化模型的公式为：求解该确定性优化模型，得到第k次迭代的最优解和最小目标函数值本发明的优势和有益效果在于以下几点：1.本发明方法，将可靠性的设计优化分解为由可靠性评估和确定性优化依次执行的顺序求解过程，避免双层嵌套的求解过程；将存在冲突的约束通过基于响应pdf的功能函数移动方法移向可靠区域，保证求出满足概率约束的最优解。该方法兼具了高精度和高效率的双重优点。2.本发明方法，在可靠性分析中使用了功能函数响应的前四阶统计矩，相较于传统的只利用一阶和二阶矩的一阶可靠性方法，利用的信息更多；虽然两者所需的计算量均较少，但是本发明方法相对来讲能够获得更加准确的计算结果。3.本发明方法，可以集成许多高级可靠性分析方法，例如双变量(或多变量)降维积分方法，多项式混沌展开方法，稀疏网格数值积分方法等，不仅能获得更高的精度，而且可以扩展应用范围，解决复杂度更高、非线性更强的工程问题。附图说明图1为本发明方法的流程框图。图2为汽车侧面碰撞有限元(fem)模型。图3为基于响应pdf的功能函数移动方法的示意图。图4为连续两次迭代响应的pdf变形近似示意图。图5为目标函数关于功能函数计算次数变化。具体实施方式下面结合附图及具体实例、采用与蒙特卡洛模拟(mcs)对比的方法对本发明作进一步详细说明，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。第一步：根据汽车轻量化设计可靠性设计优化的要求，定义数学模型。这一步需要确定系统的确定性设计变量、随机设计变量和随机参数，根据随机变量、参数的概率统计特点获得概率分布。同时要确定目标函数，建立系统功能函数，设置目标可靠度等。应对侧面碰撞防护，车辆设计必须满足政府和汽车行业关于侧面碰撞防护的规范要求。目前国内参考或使用的主要有三个的侧面碰撞防护标准：(1)中国国家标准《汽车侧面柱碰撞的乘员保护》(gb/t37337-2019)；(2)美国公路交通安全管理局对机动车安全标准的侧面碰撞测试标准(fmvss)；(3)欧洲增强型车辆安全委员会(eevc)的侧面碰撞测试标准。在本实例中，采用欧洲增强型车辆安全委员会(eevc)的侧面碰撞测试标准。假人响应侧面碰撞研究的主要指标，eevc标准对于假人响应的规定主要包括腹部峰值力(abdomenload)、肋骨变形(ribdeflection)、粘性指标(vc:viscouscriteria)、耻骨综合力(pubicsymphysisforce)和头部受伤指标(hic:headinjurycriterion)五部分。此外，由于b柱的中点速度和前门处的b柱速度也是受到极大关注的两项指标，本实例也将使用这两个指标。表1是此标准的详细信息。表1欧洲增强型车辆安全委员会(eevc)的侧面碰撞测试标准本实例的优化目标是在保证侧面碰撞的性能前提下最小化整车重量，目标可靠度取rt＝0.99。根据表1所示的安全标准和b柱的中点速度和前门处的b柱速度两项指标的标准，本实例的rbdo问题公式为：系统模型包括整车有限元模型，侧面碰撞虚拟有限元模型和侧面移动壁障模型。附图2是整车有限元模型，该模型包含85941个壳单元和96122个节点。在侧面碰撞事故的有限元模拟中，移动壁障的初始速度设置为是49.89km/h。在sgiorigin2000计算机上，进行一次有限元仿真的时间约为20小时。鉴于有限元方法高昂的计算成本，为方便计算，本实例采用最佳拉丁超立方体抽样(optimallatinhypercubesampling)和二次反向逐步回归(quadraticbackward-stepwiseregression)建立全局响应面模型。本实例建立的响应面的公式为：weight＝1.98+4.90x1+6.67x2+6.98x3+4.01x4+1.78x5+2.73x7fabdom＝1.16-0.3717x2x4-0.00931x2x10-0.484x3x9+0.01343x6x10defrib_l＝46.36-9.9x2-12.9x1x8+0.1107x3x10defrib_m＝33.86+2.95x3+0.1792x10+5.057x1x2-11.0x2x8-0.0215x5x10-9.98x7x8+22.0x8x9defrib_u＝28.98+3.818x3-4.2x1x2+0.0207x5x10+6.63x6x9-7.7x7x8+0.32x9x10vcupper＝0.261-0.0159x1x2-0.188x1x8-0.019x2x7+0.0144x3x5+0.0008757x5x10+0.08045x6x9+0.00139x8x11+0.00001575x10x11velb-pillar＝10.85-0.674x1x2-1.95x2x8+0.02054x3x10-0.0198x4x10+0.028x6x10本实例有10个概率约束，包括几何尺寸，关键零件的材料属性，移动壁障的高度和撞击位置等11个随机设计变量及参数。其中有0个确定性设计变量，9个随机设计变量(x1～x9)和2个随机参数(x10,x11)。随机设计变量和参数的名称，分布类型和参数，以及均值的变化范围如表2所示。表2随机设计变量和参数的特性第二步：设定迭代次数k＝1，设计变量初始点(μ1,μ2,…,μ9)＝(1,1,1,1,1,1,1,0.3,0.3)，随机参数均值(μ10,μ11)＝(10,10)设置允许误差ε＝0.01，功能函数pdf的移动距离令a＝1来记录功能函数编号。第三步：引入单变量降维方法，将系功能函数分解为单个随机参量的子系统，从而使计算响应原点矩的高维积分转换为一维积分。计算第a个功能函数ga(z)的前l阶原点矩ma,l(l＝1,2,3,4)表达式为：式中e{·}代表数学期望算子。对功能函数y＝ga(z)进行加性分解式中μj表示随机变量zj的均值，n表示随机变量个数。使用单变量降维方法后响应y的第l阶原点矩公式将式(4)使用二项式定理展开得到：作以下定义：则式(4)可简化成：上式的可通过下列递归公式求出：通过式(3)～(8)，可以将高维积分转化为求解数学期望这是一个一维积分。为方便描述，用qij(i＝1,…,n,j＝1,…,l)表示该积分，则有：式中是zi的概率密度函数。第四步：利用高斯系列数值积分方法计算一维积分qij，用二项式定理组合qij计算原点矩ma,l。高斯系列数值积分公式为：式中ωi,m代表权重，vi,h代表积分节点，m代表积分节点数目。由高斯系列数值积分计算所有的qij，结合式(7)～(8)，即可求出原点矩ma,l(l＝1,2,3,4)。每个一维积分使用4个积分节点。模型总共有10个功能函数，积分节点数目如表3所示：表3各功能函数的计算次数第五步：假设待估响应y的概率密度函数为则其山农熵计算公式为：使用最大熵方法(mem)求取可描述为以下优化问题：使用拉格朗日乘子法求解，构造拉格朗日函数如下：当拉格朗日函数对于概率密度函数的偏导数等于0时，式(9)取得极值，从而得到ρa(y)的解析式如下：求出拉格朗日乘子λl(l＝0,1,2,3,4)并得到响应y的pdfρ(y)后，可以通过对ρ(y)进行积分来计算约束的可靠度：第六步：令a＝a+1，重复第三～五步，直至求出所有功能函数响应的概率密度函数ρa和可靠度ra(a＝1,2,…,10)。第七步：利用基于响应pdf的功能函数移动方法，计算移动距离将可靠性优化模型改写为：式中，代表第a个功能函数响应的pdf。对于优化过程中的每一组试探点(d,μx)，都可以用第三～五步求出响应的pdf，因此是设计变量的函数，可以表示为基于响应pdf的功能函数移动方法的基本思想为：通常，可靠性设计中的可靠性要求(≥0.90)通常远高于确定性设计所实现的可靠性(≈0.5)，即概率约束比确定性约束更严格。在几何上，当目标可靠度rt＞0.5时，概率设计优化的可行域比确定性优化的可行域窄。建立等效确定性优化模型的关键在于从概率约束到确定性约束的转换，需要计算从确定性约束边界到概率约束边界的平移距离。通过平移，不满足可靠性条件的确定性约束边界移向概率约束边界，从而提高了该约束的可靠度。以概率约束p{g(x1,x2)≥0}＝rt为例，它有两个随机设计变量。如附图3所示，图中有两个坐标系：一个是设计空间，由设计变量和组成；另一个是随机空间，由随机变量x1和x2组成。最内层虚线表示的曲面是确定性设计中的约束边界g(x1,x2)＝0，平移后，得到中间细实线代表的实际设计方案的约束边界。该曲面更加靠近最外层的概率约束边界，对应的可靠度也更高。经过数次平移后，实际设计方案边界与概率设计边界重合，得到满足约束的设计方案。假设和分别是第k次和第(k+1)次迭代得到的响应的pdf。代表第k次的最优点，(d,μx)代表第(k+1)次迭代的试探点。一般而言，如附图4所示，和同时存在伸缩和平移两种变形。对于伸缩变形，pdf曲线表现为沿垂直轴伸展或收缩；而平移变形是pdf曲线显示沿水平轴平行移动。引入一个近似：和仅存在平移变形而没有伸缩变形，如附图4所示。由于在两次连续迭代中获得的候选设计点通常位于较小的邻域内，尤其是当优化设计接近收敛时，在这种情况下，响应的pdf的形状非常接近，两者的差异可视为仅有平移变形，因此进行这样的近似是合理的。基于这个近似，第k次和第k+1次迭代响应的pdf的关系为：式中，代表设计变量从变为(d,μx)时ρa(y|d,μx)的移动距离，这个距离等于功能函数值之差:为了保证满足概率约束，需要当前迭代步的约束可靠度大于或等于目标可靠度:将式(17)代入式(19)，得到：因为在第k次迭代时表达式已经求出，所以式(20)不等号左边项的大小只与的取值有关，可以定义为的函数式(20)可以改写为：通过求解上面的方程，可以获得平移距离式中arch表示函数h的逆函数。将式(18)代入式(23)得到：考虑到确定性优化约束与概率约束的不等符号相同，式(24)可以取等号。最终得到平移距离的公式为：第八步：构建确定性优化模型并求解，得到第k次迭代的最优解第k次迭代确定性优化模型的公式为：求解该确定性优化模型，得到第k次迭代的最优解和最小目标函数值第九步：判断是否成立，若成立执行第十一步；若不成立，令k＝k+1，a＝1，重复第三～九歩。第十步：输出最优解和最小目标函数值结束。采用上述步骤，经过三次迭代后达到收敛，各迭代歩得到的最优解、最小目标函数值、功能函数计算次数如表4所示。为了对比效率，使用双循环放方法求解本实例，其中双循环方法的可靠性分析与本发明方法相同，表5是两种方法的结果对比。从表4可知，所提出的方法只需2118次性能函数评估即可收敛，每个周期平均需要706次评估。与双循环方法相比，本发明方法的计算量不到它的1/15，表现出非常高的效率。同时，本方法得到的最小目标函数值与双循环方法非常接近(误差为0.9％)，表明本方法与双循环方法相近的精度。表6是收敛时各功能函数的可靠度，可以看到除了第8个约束的可靠度略微小于目标可靠度rt＝0.99(相差只有0.04％)，其他功能函数的可靠度都非常接近或超过目标可靠度，再次表明本发明方法具有非常高的精度。附图5描述了优化过程中目标函数值关于计算次数标函数的收敛过程，图中各个迭代周期彼此清晰地区分，在每个周期中，进行一次可靠性评估后再进行确定性优化。综上所述，本发明方法兼具有高精度和高效率的双重特点，值得推广。表4可靠性设计优化迭代过程表5两种方法的对比表6概率约束可靠度功能函数g1g2g3g4g5g6g7g8g9g10可靠度1.00.99011.01.01.01.01.00.98960.99970.9903本发明首先，定义了汽车侧面碰撞安全性的可靠性设计优化数学优化模型，通过概率统计等手段获取了随机设计变量和参数的概率分布特性，并建立了汽车侧面碰撞系统功能函数的响应面模型；然后，发展基于响应pdf的功能函数移动方法将传统嵌套的可靠性优化设计解耦为可靠性分析和确定性优化序列执行，即使用单变量降维方法求解响应的pdf进行可靠性分析，并计算功能函数移动量构造等效确定性优化获得更优的设计变量，上述过程重复执行直至满足收敛条件得到问题的最优解；最后，通过一个具体的汽车侧面碰撞安全分析算例验证了上述方法的可行性与高效性。本发明结合基于响应pdf的功能函数移动方法、单变量降维方法(udrm)和最大熵方法(mem)，提出了一种高效的汽车侧面碰撞安全性的可靠性设计优化方法。本发明方法与传统性方法的区别在于：利用所提出的基于响应pdf的功能函数移动方法，将可靠性分析与优化设计解耦，提高了效率；可靠性分析使用了响应的前四阶矩的信息，可以获得更高的精度，兼具有高精度和高效率的双重特点。以上内容是结合具体的优选实施方式对本发明所作的进一步详细说明，不能认定本发明的具体实施只局限于这些说明。对于本发明所属
技术领域：
的技术人员来说，在不脱离本发明构思的前提下，还可以做出若干等同替代或明显变型，而且性能或用途相同，都应当视为属于本发明的保护范围之内。当前第1页12