具有OODA分形机制的编程方法与流程

本发明涉及大规模计算机系统编程模型，特别是具有ooda分形机制的编程方法。

背景技术：

目前随着云计算技术的不断兴起，人们获取计算资源的途径也变得越来越方便和便捷。然而，解决不同计算业务，需要利用不同编程模型对问题进行建模。如：分布式计算业务需要利用mapreduce编程模型进行问题建模；深度学习业务需要利用tensorflow计算图机制，对问题进行建模；并行计算业务需要利用mpi并行计算与通信模型完成建模。因此，目前在利用编程模型对业务过程进行建模时，难以利用一种相同的编程模型，完成对各种计算问题的建模，并找到最优解决方案。

因此，亟需一种能实现计算问题做优解的建模方法。

技术实现要素：

有鉴于此，本发明提供一种具有ooda分形机制的编程方法，其特征在于：所述方法具体包括：按照业务复杂程度，将业务分为n个分形层次，并按照ooda分形编程的四个步骤，即：o1观察，o2调整，d3想定，a4行动，逐一对每一分形层实施建模，获得各个分形层的业务算子；

所述n为小于等于4的整数；n为1表示微观层次，n为2表示微观层次和中观层次，n为3表示微观层次、中观层次和宏观层次，n为4表示微观层次、中观层次、宏观层次和极限层次；

所述逐一对每一分形层实施建模即为以微观、中观、宏观和极限的顺序依次对每一分形层建模，获得微观分形层业务算子、中观分形层业务算子、宏观分形层业务算子和极限分形层业务算子。

进一步，所述微观业务算子采用下述方法获得，根据ooda分形编程的四个步骤，完成对微观业务算子的建模，具体步骤如下：

s1：o1观察，通过统一的编程标签，对需要处理的数据进行打标签；

s2：o2调整，根据整个业务的计算机理，确定最小不可分的数据计算单元；

s3：d3想定，按照业务需求中计算处理的逻辑，对业务的子任务的计算逻辑关系进行建模，形成事件算子；

s4：a4行动，根据已经完成建模的计算业务需求，利用相同或不同的计算事件单元，根据事件算子的先后执行依赖关系和数据输入输出关系，形成具有工作流依赖关系特征的微观业务算子。

进一步，步骤s4还包括在a4行动步骤中，通过全分形业务建模，可根据业务具体内容，生成与事件算子具有完全相同拓扑连接关系的微观业务算子。

进一步，步骤s4还包括在a4行动步骤中，通过非分形业务建模，生成与事件算子拓扑连接不完全相同的微观业务算子。

进一步，所述中观业务算子采用下述方法获得，根据ooda分形编程的四个步骤，完成对微观业务算子的建模，具体步骤如下：

s1：o1观察，通过统一的编程标签，对需要处理的数据进行打标签；

s2：o2调整，利用微观业务算子完成对中观业务算子的建模，保留输入和输出的打标数据接口的前提下，将微观业务算子封装，形成基础算子；

s3：d3想定，按照业务需求中计算处理的逻辑，对业务的子任务的计算逻辑关系进行建模，如数据-计算的逻辑关系，形成事件算子；

s4：a4行动，根据已经完成建模的计算业务需求，利用相同或不同的计算事件单元，根据事件算子的先后执行依赖关系和数据输入输出关系，形成具有工作流依赖关系特征的中观业务算子。

进一步，所述宏观业务算子采用下述方法获得，对已有的中观业务算子，保留输入和输出的打标数据接口，将中观业务算子封装在02调整中，在通过d3想定和a4行动构建宏观业务算子。

本发明的有益技术效果：本发明提供的具有ooda分形机制的编程方法，其利用ooda与分形建模思想，来完成各种复杂度的业务建模，从而找到各种计算问题的建模的最优解决方案；简化简单求解问题的表述方式。利用ooda四步法则对简单问题进行业务建模，完成对简单问题的求解逻辑的简洁化表达；分形拆解复杂问题。利用逐层分形方式，对复杂业务进行问题拆分，形成独立求解的简单问题。同时，结合计算机系统的分层结构，对不同层级的业务分配计算资源，为组成计算机系统的各个层级调度器，提供资源分配依据。

附图说明

下面结合附图和实施例对本发明作进一步描述：

图1基于ooda分形编程方法的微观业务算子建模原理图。

图2基于ooda分形编程产生中观业务算子的原理图。

图3基于ooda分形编程的各个分形层次图。

具体实施方式

以下结合说明书附图对本发明做出进一步的说明：

本发明提供一种具有ooda分形机制的编程方法，其特征在于：所述方法具体包括：按照业务复杂程度，将业务分为n个分形层次，并按照ooda分形编程的四个步骤，即：o1观察，o2调整，d3想定，a4行动，逐一对每一分形层实施建模，获得各个分形层的业务算子；

所述n为小于等于4的整数；n为1表示微观层次，n为2表示微观层次和中观层次，n为3表示微观层次、中观层次和宏观层次，n为4表示微观层次、中观层次、宏观层次和极限层次；

所述逐一对每一分形层实施建模即为以微观、中观、宏观和极限的顺序依次对每一分形层建模，获得微观分形层业务算子、中观分形层业务算子、宏观分形层业务算子和极限分形层业务算子。本发明提供的具有ooda分形机制的编程方法，其利用ooda与分形建模思想，来完成各种复杂度的业务建模，从而找到各种计算问题的建模的最优解决方案；简化简单求解问题的表述方式。利用ooda四步法则对简单问题进行业务建模，完成对简单问题的求解逻辑的简洁化表达；分形拆解复杂问题。利用逐层分形方式，对复杂业务进行问题拆分，形成独立求解的简单问题。同时，结合计算机系统的分层结构，对不同层级的业务分配计算资源，为组成计算机系统的各个层级调度器，提供资源分配依据。

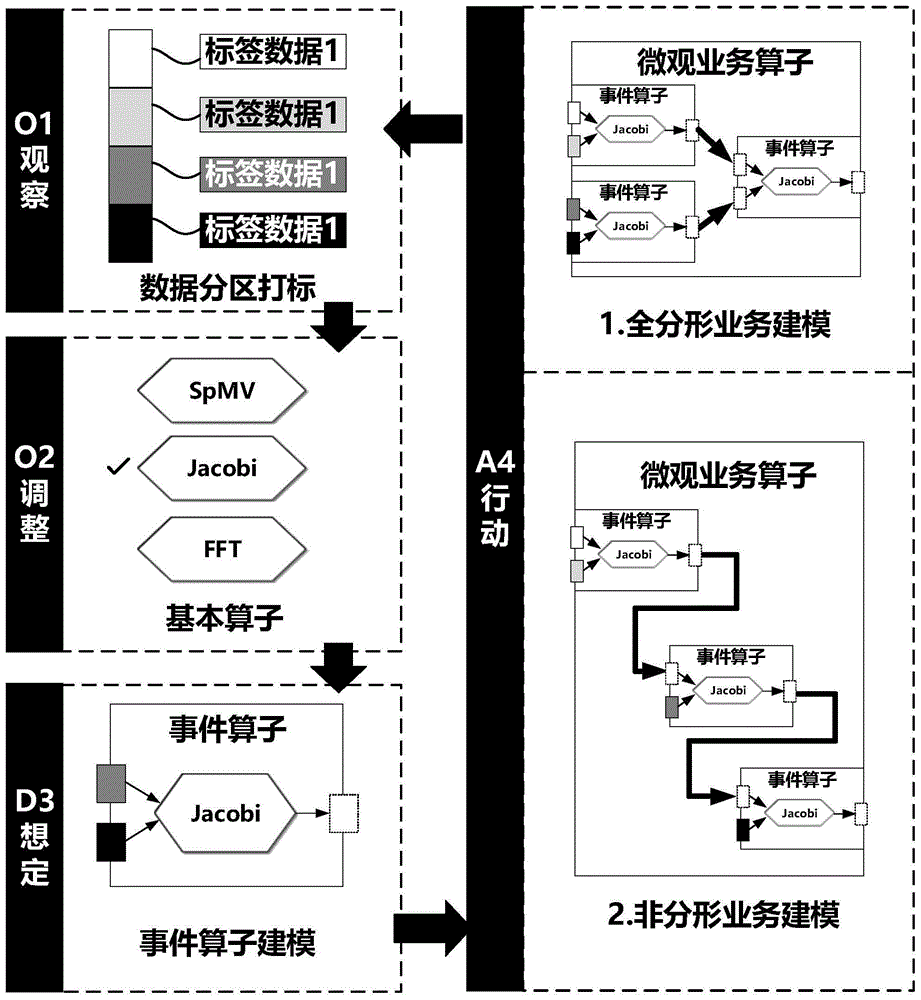
在本实施例中，所述微观业务算子采用下述方法获得，根据ooda分形编程的四个步骤，完成对微观业务算子的建模，具体步骤如下：如图1所示，

s1：o1观察，通过统一的编程标签，对需要处理的数据进行打标签；通过打标屏蔽不同计算业务处理数量结构的差异。

s2：o2调整，根据整个业务的计算机理，确定最小不可分的数据计算单元，即为基本算子；

s3：d3想定，按照业务需求中计算处理的逻辑，对业务的子任务的计算逻辑关系进行建模，形成事件算子；如图1中的黑色箭头表示“数据-计算”逻辑关系，形成“事件算子”。每个事件算子，会独立占用最小计算资源单位，如：一个进程或线程，占用一个ooda处理器的单个group(组)计算分区的alu(算术逻辑单元)，alu数量可以是单一的，也可以是多个。

s4：a4行动，根据已经完成建模的计算业务需求，利用相同或不同的计算事件单元，根据事件算子的先后执行依赖关系和数据输入输出关系，形成具有工作流依赖关系特征的微观业务算子。

在本实施例中，步骤s4还包括在a4行动步骤中，通过全分形业务建模，可根据业务具体内容，生成与事件算子具有完全相同拓扑连接关系的微观业务算子。如图2所示。

在本实施例中，步骤s4还包括在a4行动步骤中，通过非分形业务建模，生成与事件算子拓扑连接不完全相同的微观业务算子。如图2所示。

在本实施例中，所述中观业务算子采用下述方法获得，根据ooda分形编程的四个步骤，完成对微观业务算子的建模，具体步骤如下：

s1：o1观察，通过统一的编程标签，对需要处理的数据进行打标签；

s2：o2调整，利用微观业务算子完成对中观业务算子的建模，保留输入和输出的打标数据接口的前提下，将微观业务算子封装，形成基础算子；

s3：d3想定，按照业务需求中计算处理的逻辑，对业务的子任务的计算逻辑关系进行建模，如数据-计算的逻辑关系，形成事件算子；

s4：a4行动，根据已经完成建模的计算业务需求，利用相同或不同的计算事件单元，根据事件算子的先后执行依赖关系和数据输入输出关系，形成具有工作流依赖关系特征的中观业务算子。

通过ooda分形编程的四个步骤，利用微观业务算子完成对中观业务算子的建模。图2是利用全分形业务建模后，得到的微观业务算子，作为ooda分形编程的输入的一种实施例。由微观分形到“中观”。对已有的微观业务算子，在保留输入和输出的打标数据接口的前提下，封装为可在“o2调整”中选择的“事件算子”。利用封装后的事件算子，在通过想定和行动，构建出中观业务算子。

在本实施例中，所述宏观业务算子采用下述方法获得，对已有的中观业务算子，保留输入和输出的打标数据接口，将中观业务算子封装在02调整中，在通过d3想定和a4行动构建宏观业务算子。

本专利提供一种具有多分形层的建模方法。其特征如图3所示，具有如下3个特征：其一、根据最终业务的复杂程度，可经过多次ooda分形编程，完成全部的建模过程。每次ooda分形编程的过程，都与一个分形层对应。每个分型层所产生的业务算子，分别对应计算机系统结构中，不同粒度的计算部件。图3为一个复杂问题建模的实施例，包含4次ooda分形编程的建模过程。其二、对复杂问题的ooda分形编程过程中，各个分形层与计算机体系结构的资源级别一一对应。如图3所示，4个分形层次从小到大分别是：微观，中观，宏观，极限。与四个分形层次产生的算子，所对应的可在计算机系统中运行的应用程序，在计算资源调度级别也是从小到大一一对应，分别对应：处理器、计算卡、服务器主机、机群系统。例如，微观业务算子所对应应用程序，在计算机系统中运行时，则对应单个处理器所运行的程序。在资源调度时，微观业务算子所对应应用程序，会占用部分或全部单个处理器计算资源。其三、结合基于ooda分形的算子建模方法，以及基于已有业务算子产生更高层业务算子的建模方法，按照如图3中不同分形层所输入的不同类型算子，可完成对宏观业务算子和极限业务算子的建模。

ooda环(oodaloop)理论最早由美国空军上校johnboyd于1966年提出，是用于描述军事指挥决策过程的主要模型框架。ooda环依次由：观察(observe)，调整(orient)，想定(decide)，行动(act)，在内共四步以循环方式执行军事决策。ooda环理论完成决策或复杂问题的思维过程，整是人脑理性思维的思维定式。如今，ooda环理论已经不仅仅应用在军事决策方面，已经逐步成为解决各行各业关键问题的建模手段。然而，随着业务问题的不断复杂化，解决某个关键问题需要利用多次“重复”与“迭代”的方式完成。而多次“重复”与“迭代”的思维方式，正是分形思维。

最后说明的是，以上实施例仅用以说明本发明的技术方案而非限制，尽管参照较佳实施例对本发明进行了详细说明，本领域的普通技术人员应当理解，可以对本发明的技术方案进行修改或者等同替换，而不脱离本发明技术方案的宗旨和范围，其均应涵盖在本发明的权利要求范围当中。