数学口算算式题型分析方法、装置、电子设备和存储介质与流程

本申请实施例涉及搜题应用技术，尤其涉及一种数学口算算式题型分析方法、装置、设备和存储介质。

背景技术：

随着科技的进步和人们生活水平的提高，越来越多的高科技融入到人们的生活、工作和学习中。例如在教育领域，线上搜题的出现给学生、家长和教师带来了极大的便利。通过线上搜题，学生可以快速获取到题目正确答案及试题解析，教师可以确定学生对题目运算的对或错，以及时了解学生的掌握情况。

但是，数学口算算式在小学低年级数学的学习中是很重要的学习内容，而现有搜题技术中，通常是对数学运算式进行识别，然后将计算结果返回给用户。而小学低年级学生年纪比较小，无法独立看懂题目解析，也无法向家长或老师讲述计算思路。从学生的角度讲，对于算错的题目，不能明白为什么出错，假如下次遇到相同类型的题目后，仍有可能计算错误；从家长或教师的角度讲，只能获知学生对各个题目计算的对或错，不能通过全面了解题目特点来高效指导学生。

因此，现有的搜题技术在数学口算算式的应用中，只确定题目正确答案和解析，或只确定运算结果的对错的功能单一，无法多维度了解运算题目的其他特点，不利于家长或者老师指导学生真正去理解和掌握题目。

技术实现要素：

本申请提供了一种数学口算算式题型方法、装置、设备和存储介质，以解决现有口算算式搜题技术中只确定题目正确答案的方式功能单一，无法多维度了解运算题目特点，不利于家长或教师指导学生真正去理解和掌握题目的问题。

本发明采用如下技术方案：

第一方面，本申请实施例提供了一种数学口算算式题型分析方法，该方法包括：

获取口算算式文本；

识别所述口算算式文本中的运算数、运算符和括号；

根据所述运算数的数量或所述运算符的数量、所述运算数的特征、所述运算符的种类，和/或，所述括号的种类和数量，分析所述口算算式的题型。

第二方面，本申请实施例提供了一种数学口算算式题型分析装置，该装置包括：

算式文本获取模块，用于获取口算算式文本；

识别模块，用于识别所述口算算式文本中的运算数、运算符和括号；

题型分析模块，用于根据所述运算数的数量或所述运算符的数量、所述运算数的特征、所述运算符的种类，和/或，所述括号的种类和数量，分析所述口算算式的题型。

第三方面，本申请实施例提供了一种电子设备，包括存储器以及一个或多个处理器；

所述存储器，用于存储一个或多个程序；

当所述一个或多个程序被所述一个或多个处理器执行，使得所述一个或多个处理器实现如第一方面所述的数学口算算式题型分析法。

第四方面，本申请实施例提供了一种包含计算机可执行指令的存储介质，所述计算机可执行指令在由计算机处理器执行时用于执行如第一方面所述的数学口算算式题型分析方。

本发明采用的技术方案中有如下有益效果：通过获取口算算式文本，并识别口算算式文本中的运算数、运算符和括号，在利用运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型。实现了对低年级数学口算算式题型的准确判断，应用到搜题技术中，可以对运算题目进行多维度了解，有助于家长或教师根据题型特点指导学生真正去理解和掌握题目。

附图说明

通过阅读参照以下附图所作的对非限制性实施例所作的详细描述，本申请的其它特征、目的和优点将会变得更明显：

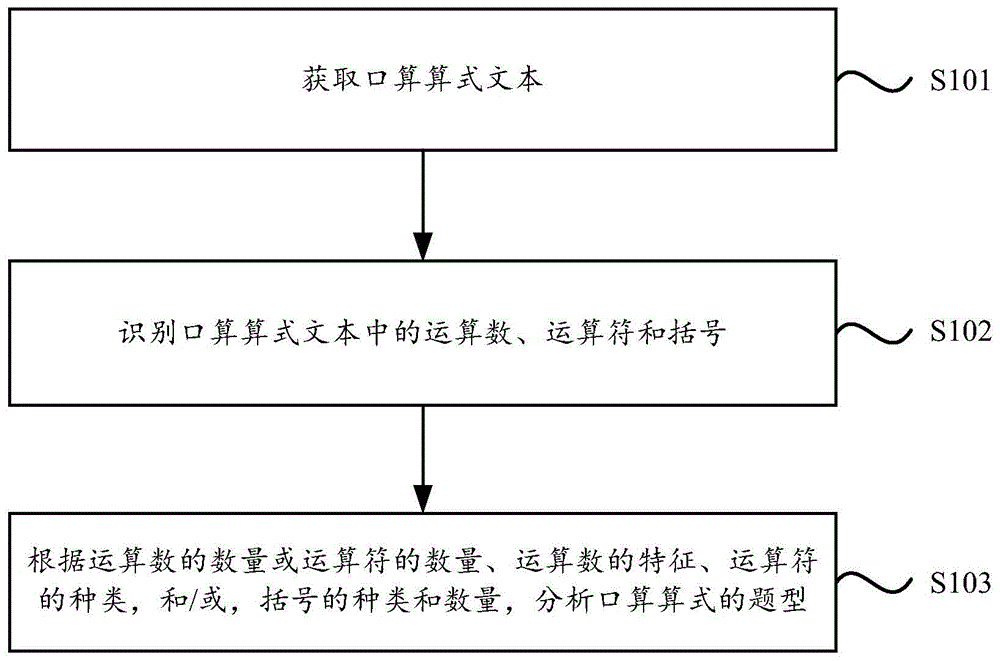
图1是本申请实施例提供的一种数学口算算式题型分析方法的流程图；

图2是本申请实施例中适用的一种题型分析结果的显示页面图；

图3是本申请实施例中适用的一种题型分析详解的显示页面图；

图4是本申请实施例提供的一种数学口算算式题型分析装置的结构示意图；

图5是本申请实施例提供的一种电子设备的结构示意图。

具体实施方式

为了使本申请的目的、技术方案和优点更加清楚，下面结合附图对本申请具体实施例作进一步的详细描述。可以理解的是，此处所描述的具体实施例仅仅用于解释本申请，而非对本申请的限定。另外还需要说明的是，为了便于描述，附图中仅示出了与本申请相关的部分而非全部内容。在更加详细地讨论示例性实施例之前应当提到的是，一些示例性实施例被描述成作为流程图描绘的处理或方法。虽然流程图将各项操作(或步骤)描述成顺序的处理，但是其中的许多操作可以被并行地、并发地或者同时实施。此外，各项操作的顺序可以被重新安排。当其操作完成时所述处理可以被终止，但是还可以具有未包括在附图中的附加步骤。所述处理可以对应于方法、函数、规程、子例程、子程序等等。

首先对本申请实施例的可应用场景进行说明。本申请实施例可以应用在低年级数学口算算式的搜题场景中，在搜出正确答案的同时，还可以分析该数学口算算式的题目类型。在现有的搜题场景中，通常只能搜题得到题目答案和/或题目答案解析，现有搜题场景中常用的方法有ai(artificialintelligence，人工智能)搜题和ocr(opticalcharacterrecognition，光学字符识别)搜题等。但是，但是，在小学低年级数学口算的应用有其独特的特点，比如，口算算式比较简单，可应用样本文本较少，导致搜题准确率低；口算算式的题目场景较多，包括试卷、练习册和家长手册。这样，由于对题库的要求较高，且研发成本和素材成本较高，导致ai搜题不能普遍应用在低年级数学口算中。另外，现有传统ocr搜题在低年级口算算式的应用中比较普遍，但其通常也是对数学运算式进行识别，然后将计算结果或解析返回给用户，对题目的其他信息推荐能力较差，其他信息比如题目的题型，而题目的题型对真正理解和掌握题目有重要的作用题型。因此，本申请实施例提供的数学口算算式题型分析可以实现了对搜题功能的扩展。

图1给出了本申请实施例提供的一种数学口算算式题型分析方法的流程图，本实施例提供的数学口算算式题型分析方法可以由数学口算算式题型分析装置来执行，该数学口算算式题型分析装置可通过硬件和/或软件的方式实现。参考图1，该方法具体可以包括：

s101、获取口算算式文本。

以低年级练习册中的数学口算为例，学生完成某个章节的练习题目、完成教师布置的作业后或者学生在遇到不会做的题目时，家长为了更好的帮助孩子理解题目，应用电子设备的搜题软件来获得题目答案、题目解析和题型，而本申请实施例的数学口算算式题型分析方法可以集成在电子设备中，通过搜题软件来执行相应的题型分析功能。

具体的，通过电子设备获取搜题文本，一种方式是可以直接获取口算算式文本，另一种方式是可以通过获取口算算式的图片并识别出文本。在一个具体的例子中，例如启动电子设备的ocr识别功能，获取目标口算算式的目标图片，可以应用ocr识别技术，将目标图片识别为口算算式文本。在一个具体的例子中，电子设备可以是学习平板或智能手机等。

s102、识别口算算式文本中的运算数、运算符和括号。

其中，一个完整的口算算式文本中包括运算数、运算符、“＝”和运算结果，是否包含括号和题型有关。比如预先存储有各个运算数、各个运算符和各个类型的括号，由于三者的文本分别具有不同的特征，因此，可以识别一个完成的口算算式文本中哪些文本是运算数、哪些文本是运算符，以及，哪些文本是括号。在实际的应用过程中，运算结果不是分析题型的必要条件，因此，这里可以识别运算结果，也可以不识别运算结果。

s103、根据运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型。

其中，通过文本匹配可以识别口算算式文本中都包括哪些运算数、哪些运算符、运算结果或什么类型的括号等。比如，预先存储有“+”、“-”、“×”和“÷”这四种运算符，将待识别的口算算式文本中的运算符进行匹配就可以确定运算符的种类。预先存储有“(”“)”“{”“}”“[”“]”等类型的括号，将待识别的口算算式文本中的括号进行匹配就可以确定括号的种类。而运算数的特征可以通过对运算数进行分析实现，例如，运算数的特征可以是一位数、两位数、三位数、0、20以下的整数或整十的倍数等。具体的，分类标准不同，确定的口算算式的题型不同。比如，多个相同的运算符就可以确定为连续运算，该相同的运算符为加法运算符时，可以确定为连加运算等。而比如改运算中的运算数均为整十的倍数，则可以确定为整十数的运算。

本发明采用的技术方案中有如下有益效果：通过获取口算算式文本，并识别口算算式文本中的运算数、运算符和括号，在利用运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型。实现了对低年级数学口算算式题型的准确判断，应用到搜题技术中，可以对运算题目进行多维度了解，有助于家长或教师根据题型特点指导学生真正去理解和掌握题目。

示例性的，根据运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型，具体还可以包括对含加法运算中的进位分析和对含减法运算中的退位分析。

若运算符中包括至少一个加法运算符，则针对每个加法运算符，提取参与加法运算的两个运算数的对应位位置的数字分别相加，判断是否有进位，若是，则口算算式的题型为有进位的运算。具体的，在低年级数学口算中，进位和退位是重点考察的一个知识点。在加法运算中，针对每个对应位置，比如，个位数字加个位数字大于或等于10，表明有进位，十位数字加十位数字大于或等于10，表明有进位。示例性的，当有两个及以上加法运算符时，则根据运算法则确定每组参与加法运算的两个运算数，再分别进行进位判断。在一个具体的例子中，5+6+1＝？，则针对第一个加法运算符，参与加法运算的两个运算数分别为5和6，相加结果11大于10，则判断有进位；针对第二个加法运算符，参与加法运算的两个运算数分别为11和1，则将两个数的个位数分别相加，十位数分别相加，来判断是否有进位。

若运算符中包括至少一个减法运算符，则针对每个减法运算符，提取参与减法运算的两个运算数的对应位位置的数字分别相减，判断是否有退位，若是，则口算算式的题型为有退位的运算。具体的，在减法运算中，针对每个对应位置，比如，被减数的个位小于减数的个位，则表明有退位，被减数的十位数字小于减数的十位数字，表明有退位。示例性的，当有两个及以上减法运算符时，则根据运算法则确定每组参与减法运算的两个运算数，再分别进行进位判断。在一个具体的例子中，25-7-9＝？，则针对第一个减号，参与减法运算的两个运算数分别为25和7，个位数相减，5小于7，则判断有进位，计算结果为18；针对第二个减号，参与减法运算的两个运算数分别为18和9，则将两个数的个位数相减，8小于9，则判断有进位。

另外，上述示例为连加或连减运算，若为加减混合运算，则判断方法相同，这里不赘述。

示例性的，根据运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型，具体包括但不限于以下情况的分析。

若运算数为两个或运算符为一个，则口算算式的题型为运算符对应的题型的基础运算。其中，运算数的数量比运算符的数量多一个，因此，如果运算数为两个，或，运算符为一个，则表明是两个运算数参与的运算，则题型为基础运算。还可以继续对运算符的种类进行判断，以确定是加法运算、减法运算、乘法运算或除法运算；还可以继续对运算数的特征进行判断，比如，运算数是否包含0、运算数是1-10、运算数是20以内、运算数是整十的倍数、运算数是三位数等。需要说明的是，判断标准可以根据教材内容确定，比如，某个版本的教材中相关章节有20以内的加减法口算，则可以将运算数是20以内作为一个题型。

若运算数为三个及以上，则口算算式的题型为连续运算。其中，如果运算数为三个及以上，表明运算符为两个及以上，则题型为连续运算。具体的，假如运算符的种类相同，比如均为加法，则为连加运算；假如运算符的种类不同，则题型为混合运算。还可以对运算数的特征进行判断，进一步细化连续运算中的题型分类，其中，运算数的特征判断方法可以参见前述实施例，在此不赘述。

若运算数包含零，则口算算式的题型为含零的运算。其中，由于低年级学生对零的概念理解程度相对较弱，在计算过程中比较容易出错，因此，可以判断运算数是否包括零，若是，则为含零的计算。这样可以进一步进行其他层面的分类去确定题型。比如，被减数中个位是0，则提示教师或家长注意该种题型的退位计算是否出错等。

若运算数为整十的倍数，则口算算式的题型为整十数的运算。其中，如果运算数为整十的倍数，则确定该类题型为整十数的运算，另外，还可以判断运算符的种类和数量，继续对题型进行细化分类。比如，整十数的加法运算和整十数的减法运算等。

若运算数的特征不同，分别确定每个运算数的特征，则口算算式的题型为与各个运算数的特征对应的运算。其中，运算数的特征进行判断，比如，运算数是否包含0、运算数是1-10、运算数是20以内、运算数是整十的倍数、运算数是三位数等。需要说明的是，判断标准可以根据教材内容确定，比如，某个版本的教材中相关章节有20以内的加减法口算，则可以将运算数是20以内作为一个类型。另外，还可以对运算符的数量和特征进行细分，确定题型。

若运算符的种类至少为两种，则口算算式的题型为混合运算。其中，判断运算符的种类，在运算符的种类至少为两种时，确定口算算式的题型为混合运算。可选的，具体包括但不限于以下几种情况：若运算符包括加法运算符和减法运算符，则口算算式的题型为加减混合运算；若运算符包括乘法运算符和除法运算符，则口算算式的题型为乘除混合运算；若运算符号包括加法运算符和减法运算符中的至少一个，以及，乘法运算符和除法运算符中的至少一个，则口算算式的题型为加减乘除混合运算。示例性的，考虑到低年级学生对乘法和除法的理解程度相对较弱，另外，运算法则也是需要重点掌握的知识点，比如先算乘除后算加减，因此，在混合运算中，将含有乘法和除法的题型进行分类。

若口算算式文本中包括括号，则口算算式的题型为带括号的运算。其中，括号主要包括小括号“(”和“)”、大括号“{”和“}”，以及，中括号“[”和“]”。带括号的题型，可以提示教师或家长注意学生是否在口算过程中注意到括号的存在，或者，注意是否存在由于没仔细看到括号带来的计算错误的情况。从运算法则的角度出发，优先计算括号中运算内容。

示例性的，还包括：若运算符中包括至少一个乘法运算符，则判断参与乘法运算的两个运算数的特征，若两个运算数均为一位数，则运算的题型的包含乘法口诀的计算。其中，对应乘法运算，还可以细分为多种运算题型，其中，参与乘法运算的两个运算数均为一位数，则运算的题型为包含乘法口诀的运算。该类题型有助于帮助教师和家长了解学生对乘法口诀的掌握情况。

示例性的，若运算数包含零，则口算算式的题型为含零的运算中，若运算数包含零，且，零参与的运算为乘法运算，则口算算式的题型为含零的乘法运算。具体的，对于运算数包含零的运算，如果运算符不同，则可以确定不同的题型，每个题型中对零的定位不同。其中，如果有零参与的乘法运算，则确定口算算式的题型为含零的乘法运算。该类题型有助于教师了解学生对零乘以任何数都得零的知识点的掌握。另外，在有零参与的除法运算中，还可以确定题型为含零的除法运算。

在一个具体的例子中，口算算式为15+78＝93，匹配算式{a}#{b}＝{r}，匹配运算符#为+，运算数的取值范围[10,99}，这样能匹配到的题型是两位数加两位数。然后判断是否有进位，提取运算数个位相加为1+7＝8，小于10，提取运算数十位相加为5+8＝13，大于10，确定有进位，则可以判断该题型为带进位的两位数加两位数运算。示例性的，图2示出了一种题型分析结果的显示页面图，图3示出了一种题型分析详解的显示页面图，点击图3中的“题型分析详解”的图标，可跳转至图3的题型分析详解的显示页面。

需要说明的是，题型的分类没有唯一的标准，具体可以根据学生的出错频率或者教学大纲中的知识点进行分类；而且，同一个题型，按照运算数的特征进行分类，或者，按照运算符的种类或者特征进行分类，或者，同时按照上述两种标准进行分类，得到的题型确定结果可能不同，可能某个题型是包含另一个题型的，比如，连加题型包括20以内的连加的题型。因此，上述几种题型只是举例说明，并不形成具体的限定。

在实际的应用过程中，更细化的题型可以包括：1-10的加法或减法运算、含零的加法或减法运算、连加或连减运算、加减混合运算、十几和十几的加减混合运算、20以内的进位加法运算、20以内的退位减法运算、整十数加法或减法运算、两位数加减一位数运算、两位数加减整十数运算、加减混合或连加连减中包括小括号的运算、不进位的两位数加两位数运算、进位的两位数加两位数运算、退位的两位数减两位数的运算、包含乘法口诀的运算、乘加或乘减运算、用2-6的乘法口诀求商的运算、加减乘除混合运算、笔算几百几十加几百几十的运算、三位数加两位数或三位数的运算、不退位的三位数减三位数的运算、退位的三位数减两位数的运算、被减数中间有零的退位减法以及利用减法为减法验算的运算、零乘一个数的运算、三位数乘以一位数或两位数的运算、以及，除数是两位数的除法运算等。可以应用不同的分析标准或分析条件来对题型进行分析或判断。

在一个具体的例子中，表1示出了一种各题型特征表，其中，{a}、{b}、{c}表示对应的运算数，#表示运算符，{r}表示运算结果；{+}、{-}、{×}、{÷}表示运算符；||表示或；&&表示与；最大运算数即为运算数中的最大值；最小运算数即为运算数中的最小值；true表示是，false表示否。

表1各题型特征表

需要说明的是，由于篇幅限制，表1显示在了两页中，实际均为表1中的表格内容。

在上述实施例的基础上，图4为本申请实施例提供的一种数学口算算式题型分析装置的结构示意图。参考图4，本实施例提供的数学口算算式题型分析装置具体包括：算式文本获取模块401、识别模块402和题型分析模块403。

其中，算式文本获取模块401，用于获取口算算式文本；识别模块402，用于识别口算算式文本中的运算数、运算符和括号；题型分析模块403，用于根据运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型。

本发明采用的技术方案中有如下有益效果：通过获取口算算式文本，并识别口算算式文本中的运算数、运算符和括号，在利用运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型。实现了对低年级数学口算算式题型的准确判断，应用到搜题技术中，可以对运算题目进行多维度了解，有助于家长或教师根据题型特点指导学生真正去理解和掌握题目。

可选的，算式文本获取模块401具体用于：

获取目标口算算式的目标图片；

将目标图片识别为口算算式文本。

可选的，题型分析模块403包括进位分析子模块和退位分析子模块，其中：

进位分析子模块用于：在运算符中包括至少一个加法运算符时，针对每个加法运算符，提取参与加法运算的两个运算数的对应位位置的数字分别相加，判断是否有进位，若是，则确定口算算式的题型为有进位的运算；

退位分析子模块用于：在运算符中包括至少一个减法运算符时，针对每个减法运算符，提取参与减法运算的两个运算数的对应位位置的数字分别相减，判断是否有退位，若是，则确定口算算式的题型为有退位的运算。

可选的，题型分析模块403包括运算数类型分析子模块、运算符类型分析子模块和运算括号分析子模块，其中：

运算数类型分析子模块用于：在运算数为两个或运算符为一个时，确定口算算式的题型为运算符对应的题型的基础运算；在运算数为三个及以上时，确定口算算式的题型为连续运算；在运算数包含零时，确定口算算式的题型为含零的运算；在运算数为整十的倍数时，确定口算算式的题型为整十数的运算；在运算数的特征不同时，分别确定每个运算数的特征，并确定口算算式的题型为与各个运算数的特征对应的运算。

运算符类型分析子模块用于：在运算符的种类至少为两种时，确定口算算式的题型为混合运算；

运算括号分析子模块用于：在口算算式文本中包括括号时，确定口算算式的题型为带括号的运算。

可选的，运算符类型分析子模块具体用于：

在运算符包括加法运算符和减法运算符时，确定口算算式的题型为加减混合运算；

在运算符包括乘法运算符和除法运算符时，确定口算算式的题型为乘除混合运算；

在运算符号包括加法运算符和减法运算符中的至少一个，以及，乘法运算符和除法运算符中的至少一个时，确定口算算式的题型为加减乘除混合运算。

可选的，运算数类型分析子模块具体用于：

在运算符中包括至少一个乘法运算符时，判断参与乘法运算的两个运算数的特征，若两个运算数均为一位数，则运算的题型的包含乘法口诀的计算。

可选的，运算数类型分析子模块具体用于：

在运算数包含零，且，零参与的运算为乘法运算时，口算算式的题型为含零的乘法运算。

本申请实施例提供的数学口算算式题型分析装置可以用于执行上述实施例提供的数学口算算式题型分析方法，具备相应的功能和有益效果。

本申请实施例提供了一种电子设备，且该电子设备中可集成本申请实施例提供的数学口算算式题型分析装置。图5是本申请实施例提供的一种电子设备的结构示意图。参考图5，该电子设备包括：处理器50、存储器51。该电子设备中处理器50的数量可以是一个或者多个，图5中以一个处理器50为例。该电子设备中存储器51的数量可以是一个或者多个，图5中以一个存储器51为例。该电子设备的处理器50和存储器51可以通过总线或者其他方式连接，图5中以通过总线连接为例。

存储器51作为一种计算机可读存储介质，可用于存储软件程序、计算机可执行程序以及模块，如本申请任意实施例所述的数学口算算式题型分析方法对应的程序指令/模块(例如，数学口算算式题型分析装置中的算式文本获取模块401、识别模块402和题型分析模块403)。存储器51可主要包括存储程序区和存储数据区，其中，存储程序区可存储操作系统、至少一个功能所需的应用程序；存储数据区可存储根据设备的使用所创建的数据等。此外，存储器51可以包括高速随机存取存储器，还可以包括非易失性存储器，例如至少一个磁盘存储器件、闪存器件、或其他非易失性固态存储器件。在一些实例中，存储器51可进一步包括相对于处理器50远程设置的存储器，这些远程存储器可以通过网络连接至设备。上述网络的实例包括但不限于互联网、企业内部网、局域网、移动通信网及其组合。

处理器50通过运行存储在存储器51中的软件程序、指令以及模块，从而执行设备的各种功能应用以及数据处理，即实现上述的数学口算算式题型分析方法，该数学口算算式题型分析方法包括：获取口算算式文本；识别口算算式文本中的运算数、运算符和括号；根据运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型。

上述提供的设备可用于执行上述实施例提供的数学口算算式题型分析方法，具备相应的功能和有益效果。

本申请实施例还提供一种包含计算机可执行指令的存储介质，所述计算机可执行指令在由计算机处理器执行时用于执行一种数学口算算式题型分析方法，该数学口算算式题型分析方法包括：获取口算算式文本；识别口算算式文本中的运算数、运算符和括号；根据运算数的数量或运算符的数量、运算数的特征、运算符的种类，和/或，括号的种类和数量，分析口算算式的题型。

存储介质——任何的各种类型的存储器设备或存储设备。术语“存储介质”旨在包括：安装介质，例如cd-rom、软盘或磁带装置；计算机系统存储器或随机存取存储器，诸如dram、ddrram、sram、edoram，兰巴斯(rambus)ram等；非易失性存储器，诸如闪存、磁介质(例如硬盘或光存储)；寄存器或其它相似类型的存储器元件等。存储介质可以还包括其它类型的存储器或其组合。另外，存储介质可以位于程序在其中被执行的第一计算机系统中，或者可以位于不同的第二计算机系统中，第二计算机系统通过网络(诸如因特网)连接到第一计算机系统。第二计算机系统可以提供程序指令给第一计算机用于执行。术语“存储介质”可以包括可以驻留在不同位置中(例如在通过网络连接的不同计算机系统中)的两个或更多存储介质。存储介质可以存储可由一个或多个处理器执行的程序指令(例如具体实现为计算机程序)。

当然，本申请实施例所提供的一种包含计算机可执行指令的存储介质，其计算机可执行指令不限于如上所述的数学口算算式题型分析方法，还可以执行本申请任意实施例所提供的数学口算算式题型分析方法中的相关操作。

上述实施例中提供的数学口算算式题型分析装置、存储介质及设备可执行本申请任意实施例所提供的数学口算算式题型分析方法，未在上述实施例中详尽描述的技术细节，可参见本申请任意实施例所提供的数学口算算式题型分析方法。

注意，上述仅为本申请的较佳实施例及所运用技术原理。本领域技术人员会理解，本申请不限于这里所述的特定实施例，对本领域技术人员来说能够进行各种明显的变化、重新调整和替代而不会脱离本申请的保护范围。因此，虽然通过以上实施例对本申请进行了较为详细的说明，但是本申请不仅仅限于以上实施例，在不脱离本申请构思的情况下，还可以包括更多其他等效实施例，而本申请的范围由所附的权利要求范围决定。