一种目标近场雷达回波的快速仿真方法与流程

本发明属于电磁计算技术领域，具体涉及一种目标近场雷达回波的快速仿真方法。

背景技术：

目标的近场电磁散射特性研究是基于无线电引信相关技术为背景发展起来的，在精确制导、电磁兼容等领域发挥着重要作用。在近场条件下，雷达回波需要考虑入射场的非平面波效应、距离以及局部照射。此外，在相关应用中，目标与天线之间还存在高速运动，诸多因素的影响加大了近场雷达回波研究的难度。

现有技术获取目标近场雷达回波，主要通过实际测量和数值仿真。其中，实际测量即在外场或者微波暗室开展实验获取雷达回波，需要有比较完备的测试系统、测试理论和数据处理技术支撑；而数值仿真则通过数值方法求解满足特定边界条件的麦克斯韦方程组，计算出相应的散射场回波。根据精度和效率，数值方法又分为高频近似法和全波数值法两类。

然而，现有技术具有以下缺陷：

1、实际测量对场地要求高、所受的干扰因素多、测试周期长，不可避免地限制了其实际应用。

2、数值方法中，高频近似数值方法方法无法精确描述目标的细微结构，对复杂目标的计算结果与实际测量结果有偏差。而传统的全波数值法计算每个场点的散射回波都需要对整个目标的表面等效电磁流积分，对大片雷达近场回波观察区的计算非常耗时。

3、每次测量或仿真得到的不同状态下的雷达回波数据不具备可重复利用性。

综上，现有求解近场散射回波技术整体而言存在效率不高、精度不足、不够灵活等问题，迫切需要开发新的技术解决近场散射回波的快速准确计算。

技术实现要素：

有鉴于此，本发明提供了一种目标近场雷达回波的快速仿真方法，能解决近场散射回波的快速准确计算。

实现本发明的技术方案如下：

一种目标近场雷达回波的快速仿真方法，包括以下步骤：

步骤一、利用低秩分解方法压缩频率、极化、入射角度、天线方向图得到基状态空间；

步骤二、数值求解不同基状态的入射场照射下，目标表面的等效电磁流分布；

步骤三、建立一个包围体，将近场回波观察区包围起来，并采用四面体网格对该包围体进行剖分；

步骤四、计算入射状态为p时的四面体网格棱边i的中点的切向散射场；将四面体网格所有棱边中点的切向散射场表示为公式(2)所示的形式；

dm×p＝lm×n·jn×p+km×n·mn×p(1)

其中，m为所有四面体非重复棱边总数，n代表离散等效电磁流所需的基函数个数，p表示基状态总数，p＝1,2,...,p，jn×p表示等效电流矩阵，mn×p表示等效磁流矩阵；lm×n和km×n均为近场阻抗矩阵，矩阵dm×p即为近场散射数据库；

对所述近场阻抗矩阵lm×n和km×n进行压缩；

将压缩后的近场阻抗矩阵和jn×p以及mn×p相乘，获得近场散射数据库dm×p；

步骤五、建立二分查找树，快速查找任意场点所属的四面体；

步骤六、将实际入射场的状态表示为基状态的叠加，并从数据库中提取该场点所属四面体各棱边的切向场dmk,p，使用边缘元基函数n(r)，插值得到各场点的近场回波。

进一步地，所述建立二分查找树采用如下递归过程完成：

建立四面体集合的外接长方体盒子；

选择外接长方体x,y,z最长的方向，对每个四面体重心在该方向的坐标值排序；

对排序后的四面体重心等分，相应的四面体集合也随之等分，得到树的两个子节点；

递归直到每节点只含有一个四面体；

查找过程采用如下过程完成：

从根结点开始，判断场点是否在该节点外接盒子内部；

如果场点不在外接盒子内部，跳过该节点及其子节点的查找，否则判断该节点是否只含一个四面体；

若场点在外接盒子内部，且该节点只含一个四面体，查找完成；否则继续对该节点的子节点重复上述查找过程。

进一步地，采用多层矩阵分解算法或多层快速多极子技术对所述近场阻抗矩阵lm×n和km×n进行压缩。

有益效果：

1、本发明利用数据库的思想，压缩众多入射状态量得到基状态空间，根据基状态空间建立目标近场散射数据库，提高了数据的复用，避免了费时的临时计算。

2、本发明方法提出近场回波数据库快速构建和快速检索技术，使得观察区域任意场点的回波能够快速准确获得。因此，本发明能够有效解决近场散射回波计算精度差、计算效率低和灵活性不足的问题。

附图说明

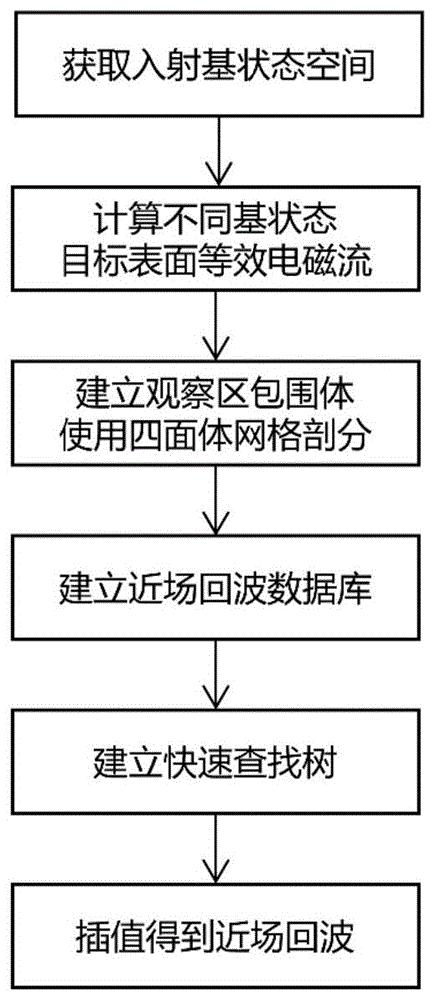
图1、本发明方法总体流程图。

图2、本发明中集群树、块集群树和分层矩阵示意图。

图3、本发明的多层矩阵分解示意图。

图4、本发明中四面体边缘元插值示意图。

具体实施方式

下面结合附图并举实施例，对本发明进行详细描述。

本发明提供了一种目标近场雷达回波快速仿真方法，具体是指一种基于近场散射数据库快速生成与检索的近场回波快速仿真方法。该方法如图1所示，包含以下步骤：

步骤一：获取入射基状态空间。利用低秩分解方法，例如骨元技术，压缩频率、极化、入射角度、天线方向图等不同入射状态量，得到完备的基状态空间，作为近场散射数据库的检索字段。

步骤二：数值求解不同基状态的入射场照射下，目标表面的等效电磁流分布。求解等效电磁流的方法可用常规数值方法完成，诸如物理光学法、矩量法、合元极法等。求得的等效电流和磁流矩阵分别表示为jn×p和mn×p。其中n代表离散等效电磁流所需的基函数个数，p表示基状态总数，矩阵元素代表等效电磁流的基函数展开系数。

步骤三：建立一个包围体，将近场回波观察区包围起来，并采用四面体网格对该包围体进行剖分。该包围体要求略大于待求区域，四面体网格尺寸可设置为0.05λ0～0.1λ0，λ0表示自由空间的波长。

步骤四：建立近场散射回波数据库。具体的，

步骤4.1、入射状态p，四面体棱边i的中点的切向散射场可以用(1)式求解

其中，k0代表自由空间的波数，z0为自由空间波阻抗，g是自由空间的格林函数，r,r′分别是场点和源点(目标表面离散点)坐标,是四面体棱边i的单位方向矢量。fj(r′)代表展开电磁流的基函数，p＝1,2,...,p，以rwg基函数为例，此时分布有等效电磁流的目标表面被三角形网格离散，积分在每个rwg所定义的一对三角形上进行。jjp和mjp分别代表通过步骤二得到的基状态为p时等效电、磁流的基函数展开系数，j＝1,2,...,n，和分别代表作用在场点和源点的微分算子,s′代表源点分布的曲面。

步骤4.2、将四面体网格所有棱边中点的切向散射场的计算表示为公式(2)所示矩阵相乘求和的形式

dm×p＝lm×n·jn×p+km×n·mn×p(3)

其中，m为所有四面体非重复棱边总数，lm×n和km×n称为近场阻抗矩阵，其矩阵元素如公式(1)中所述。矩阵dm×p即为近场散射数据库。

步骤4.3、采用多层矩阵分解算法对公式(2)中所述近场阻抗矩阵lm×n和km×n进行压缩。

采用如下过程完成：

(1)建立集群树。如图2所示，对场点和源点按照最长尺寸方向递归二分，得到集群树ti,tj；

(2)建立块集群树。从根到叶，每个场集群t和同一层的源集群s可以构成一个块集群t×s。该块集群需要继续细分，如果构成该块集群的源集群和场集群非完全分离。该过程直到集群树的最细层为止，最终得到一棵块集群树ti×j。如图2所示，块集群树将对应一个分层矩阵，完全分离的块集群对应着分层矩阵的可容块，最细层不完全分离的块集群对应分层矩阵的不可容块。

(3)填充分层矩阵。不可容块的填充直接采用公式(1)计算，可容块的填充采用多层矩阵分解算法填充，最终，近场阻抗矩阵压缩存储如下

其中，是块集群t×s对应的维度为m×n的子矩阵，fm×n为满阵，l是矩阵分解层数，rq,q＝0,...,l+1是分块稀疏矩阵，图3展示了一个分解层数为3层的多层矩阵分解的示意图。

近场阻抗矩阵l,k的压缩，也可采用多层快速多极子技术，典型步骤是聚集、转移和发散。其中，聚集只在源点进行，发散只在场点进行，转移矩阵从源点到场点单方向进行。

步骤4.4、求解近场散射数据库，具体操作是将压缩过后近场阻抗矩阵和电磁流矩阵相乘，获得近场散射数据库dm×p。

步骤五：建立二分查找树，快速查找任意场点所属的四面体。

建立查找树采用如下递归过程完成：

(1)建立四面体集合的外接长方体盒子

(2)选择外接长方体x,y,z最长的方向，对每个四面体重心在该方向的坐标值排序；

(3)对排序后的四面体重心等分，相应的四面体集合也随之等分，得到树的两个子节点；

(4)递归直到每节点只含有一个四面体

查找过程采用如下过程完成：

从根结点开始，判断场点是否在该节点外接盒子内部；

如果场点不在外接盒子内部，跳过该节点及其子节点的查找，否则判断该节点是否只含一个四面体；

若场点在外接盒子内部，且该节点只含一个四面体，查找完成；否则继续对该节点的子节点重复上述查找过程。

步骤六：利用数据库插值得到各场点的近场回波。具体操作是将实际入射场的状态表示为基状态的叠加，并从数据库中提取该场点所属四面体各棱边的切向场如图4所示，使用边缘元基函数n(r)，插值得到各场点的近场回波。插值过程可用公式(4)表述

综上，本发明提出一种基于数据库技术的目标近场雷达回波获取技术，实现了不同状态下近场回波的快速计算；利用多层矩阵分解或多层快速多极子技术，能够快速获得近场散射数据库；建立快速查找树，能够快速检索数据库，准确获取观察区任一场点的近场回波。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。