隧道局部变形识别方法及装置与流程
本申请涉及隧道检测技术领域,尤其涉及一种隧道局部变形识别方法及装置。
背景技术:
本部分旨在为权利要求书中陈述的本发明实施例提供背景或上下文。此处的描述不因为包括在本部分中就承认是现有技术。
隧道结构主要由洞身、洞门组成。为防止围岩变形或坍塌,沿洞身周边用钢筋混凝土等材料构建的永久性支护结构称为衬砌,沿线路长度方向,衬砌一般分节段设置,节段之间设置接缝。圆形或椭圆形是洞身主要的断面形式。为提高隧道结构寿命和安全性,需要定期对隧道结构开展状态评估,其中隧道洞身衬砌变形是表征结构受力和隧道稳定性的重要指标。
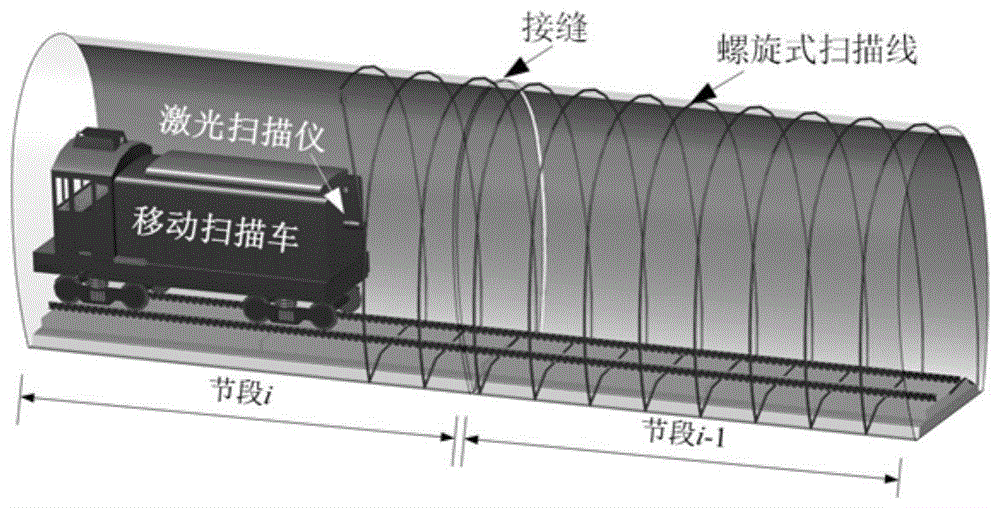
采集洞身衬砌轮廓几何信息是开展隧道结构变形分析的基础工作。因具有测量精度高、非接触等优点,三维激光扫描技术广泛应用在建设期或运营期隧道几何信息采集,按测量方式的不同三维激光扫描技术主要分为逐站联测和移动式两种类型,逐站联测主要应用在隧道建设期,移动式扫描具有测量效率高、交通干扰小等优点,主要应用在运营期,移动式扫描的工作原理如图1所示。
国内外技术人员围绕隧道三维扫描数据开展了大量研究,主要集中在采用圆、椭圆对隧道断面进行拟合,获取轮廓圆心和半径,上述方法适用于分析隧道结构整体变形,如因围岩变形引起的断面收敛变化以及因地质活动引起的区域范围内(连续数个节段)隧道整体变形;事实上,隧道结构除发生上述整体变形外,单个节段在局部围岩条件发生改变时(如偏压、拱顶岩体坠落等),洞身衬砌还会发生局部变形,相较于隧道整体变形,洞身衬砌的局部变形更易迫使结构受力或隧道稳定趋于不安全状态。传统的圆、椭圆断面拟合方法对节段局部变形不敏感。
技术实现要素:
本申请实施例提供一种隧道局部变形识别方法,用以提高隧道节段的局部变形识别精度,该方法包括:
将隧道每个节段划分为多个单元,获取每个单元上当前点群中各个空间点在大地坐标系下的当前大地坐标,以及每个节段的历史基准轴线和每个单元上历史点群中各个空间点的历史大地坐标;根据每个单元上当前点群中各个空间点的当前大地坐标,确定每个节段的当前轴线;调整当前轴线与历史基准轴线平行且当前轴线的中点与历史基准轴线的中点重合,将每个单元上当前点群中各个空间点的大地坐标转换为当前轴线平行于历史基准轴线且当前轴线的中点与历史基准轴线的中点重合时的转换坐标;根据每个单元上当前点群中各个空间点的转换坐标,确定当前点群中各个空间点在垂直于历史基准轴线的平面上的当前投影点坐标,并利用nurbs拟合得到当前投影拟合函数;根据每个单元上历史点群中各个空间点的历史大地坐标,确定历史点群中各个空间点在垂直于历史基准轴线的平面上的历史投影点坐标,并利用nurbs拟合得到历史投影拟合函数;确定拟合圆的圆心坐标、拟合圆上指定点的局部坐标、拟合圆上指定点在当前投影拟合函数上的当前最佳投影点坐标,以及在历史投影拟合函数上的历史最佳投影点坐标,其中,所述拟合圆由每个单元上当前点群中各个空间点在与历史基准轴线垂直的平面上的投影点拟合得到;根据当前最佳投影点坐标、历史最佳投影点坐标、拟合圆上的指定点的局部坐标及拟合圆的圆心坐标确定拟合圆上该指定点处隧道局部变形参数;如果隧道局部变形参数不等于0,则确定隧道局部发生变形,并将隧道局部变形参数的绝对值确定为隧道变形量。
在一种实现方式中,将每个单元上当前点群中各个空间点的大地坐标转换为当前轴线平行于历史基准轴线且当前轴线的中点与历史基准轴线的中点重合时的转换坐标,包括:根据(x(0),y(0),z(0))t=r1(x(1),y(1),z(1))t+t1确定各个空间点的大地坐标(x(1),y(1),z(1))对应的转换坐标(x(0),y(0),z(0));其中,r1表示空间旋转矩阵,r1=r(γ)·r(τ)·r(β),
在一种实现方式中,根据每个单元上当前点群中各个空间点的转换坐标,确定当前点群中各个空间点在垂直于历史基准轴线的平面上的当前投影点坐标,并利用nurbs拟合得到当前投影拟合函数,包括:在每个单元中心建立与历史基准轴线垂直的垂直平面,将每个单元上当前点群中各个空间点投影到垂直平面上,得到当前点群中各个空间点对应的当前投影点;以历史基准轴线与垂直平面的交点为原点,构建局部坐标系,根据当前点群中空间点的转换坐标确定局部坐标系下当前投影点的局部坐标;利用当前投影点拟合圆,根据当前投影点的局部坐标确定拟合圆的圆心和圆心坐标,以拟合圆的圆心为中心,以预设角度为圆心角,将拟合圆划分为多个扇形;根据每个扇形范围内投影点的局部坐标确定每个扇形范围内投影点的特征点,对所有扇形范围内的特征点进行nurbs拟合,得到当前投影拟合函数。
在一种实现方式中,根据每个扇形范围内投影点的局部坐标确定每个扇形范围内投影点的特征点,包括:计算每个扇形范围内所有投影点的局部坐标的平均值,将计算得到的平均值对应的点作为每个扇形范围内投影点的特征点。
在一种实现方式中,指定点为拟合圆上划分的扇形的角平分线与拟合圆的交点;确定拟合圆上的指定点的局部坐标,包括:根据
在一种实现方式中,根据当前最佳投影点坐标、历史最佳投影点坐标、拟合圆上的指定点的局部坐标及拟合圆的圆心坐标确定拟合圆上该指定点处隧道局部变形参数,包括:根据
在一种实现方式中,根据每个单元上当前点群中各个空间点在大地坐标系下的大地坐标,确定每个节段的当前轴线,包括:针对每个节段,在节段的拱顶两端各选择一个目标点,根据两个目标点的大地坐标确定初始单位方向矢量;沿初始单位方向矢量的方向,将每个节段划分为等长度的多个单元,在每个单元中心构建与初始单位方向矢量垂直的平面,作为投影平面;将投影平面与初始单位方向矢量的交点作为原点,构建局部坐标系;将每个单元上每个点投影到投影平面,将投影到指定范围内的投影点确定为有效点;将有效点的大地坐标转换为局部坐标系下的局部坐标;利用每个单元的有效点在投影平面上拟合圆,确定拟合圆的圆心局部坐标;将圆心局部坐标转换为圆心大地坐标;将每个节段所有单元的圆心大地坐标进行空间直线拟合,得到第一轴线;根据第一轴线确定第一单位方向矢量;利用根据初始单位方向矢量确定第一轴线和第一单位方向矢量的方法,根据第一单位方向矢量确定每个节段的第二轴线和第二单位方向矢量;确定第一单位方向矢量与第二单位方向矢量的偏差;如果所述偏差小于等于偏差阈值,则将第二轴线确定为该节段隧道的当前轴线。
在一种实现方式中,两个目标点分别为ps(xs,ys,zs)、pe(xe,ye,ze),根据两个目标点的大地坐标确定初始单位方向矢量,包括:根据vt=(xt,yt,zt)=(xe-xs,ye-ys,ze-zs)/s计算初始单位方向矢量vt;其中,s为ps至pe向量的模,
在一种实现方式中,将投影平面与初始单位方向矢量的交点作为原点,构建局部坐标系,包括:将投影平面与初始单位方向矢量的交点作为局部坐标系的原点,将大地坐标系中x轴方向作为局部坐标系的y轴方向,将大地坐标系中指向竖向高程的z轴在投影平面上投影的反方向作为局部坐标系的x轴方向,将初始单位方向矢量的方向作为局部坐标系的z轴方向,构建局部坐标系。
在一种实现方式中,在将投影到指定范围内的投影点确定为有效点之前,所述方法还包括:在所有投影点中沿y轴方向选择间距最大的两个点作为纵轴外边缘点,沿x轴方向选择隧道拱顶的一个点作为横轴外边缘点,利用两个纵轴外边缘点和一个横轴外边缘点确定外边界圆,得到外边界圆的圆心和半径;根据δd=α(δl|zt|+2δ)确定预设偏移量δd;其中,α表示经验系数;δl表示单元的长度;|zt|表示初始单位方向矢量的分项绝对值;δ表示隧道大地坐标测量系统的测距精度;将与外边界圆共圆心,半径小于外边界圆半径预设偏移量的圆确定为内边界圆;将内边界圆和外边界圆构成的圆环确定为指定范围。
在一种实现方式中,在将有效点的大地坐标转换为局部坐标系下的局部坐标之前,所述方法还包括:根据(xse-j,yse-j,zse-j)=(j-0.5)svt/m+(xs,ys,zs)确定投影平面与初始单位方向矢量的交点pse-j的坐标(xse-j,yse-j,zse-j);其中,j表示划分的第j个单元,j=1,2,...,m,m表示节段划分的单元的总数量;所述将有效点的大地坐标转换为局部坐标系下的局部坐标,包括:根据
在一种实现方式中,将每个节段所有单元的圆心坐标进行空间直线拟合,得到第一轴线;根据第一轴线确定第一单位方向矢量,包括:构建第一轴线的参数方程
在一种实现方式中,所述确定第一单位方向矢量与第二单位方向矢量的偏差,包括:根据c=1-v(t0)·v(t1)=1-xt0xt1-yt0yt1-zt0zt1确定第一单位方向矢量v(t0)与第二单位方向矢量v(t1)的偏差c,其中,(xt1,yt1,zt1)为第二单位方向矢量v(t1)的大地坐标。
在一种实现方式中,在确定第一单位方向矢量与第二单位方向矢量的偏差之后,所述方法还包括:如果所述偏差大于偏差阈值,则将第二单位方向矢量作为新的第一单位方向矢量,根据新的第一单位方向矢量计算新的第二单位方向矢量和第二轴线,直至计算得到的第一单位方向矢量与第二单位方向矢量的偏差小于等于偏差阈值,将最后一次计算得到的第二轴线确定为该节段隧道的隧道轴线。
本申请实施例还提供一种隧道局部变形识别装置,用以提高隧道节段的局部变形识别精度,该装置包括:
获取模块,用于将隧道每个节段划分为多个单元,获取每个单元上当前点群中各个空间点在大地坐标系下的当前大地坐标,以及每个节段的历史基准轴线和每个单元上历史点群中各个空间点的历史大地坐标;确定模块,用于根据获取模块获取的每个单元上当前点群中各个空间点的当前大地坐标,确定每个节段的当前轴线;坐标转换模块,用于调整确定模块确定的当前轴线与获取模块获取的历史基准轴线平行且当前轴线的中点与历史基准轴线的中点重合,将每个单元上当前点群中各个空间点的大地坐标转换为当前轴线平行于历史基准轴线且当前轴线的中点与历史基准轴线的中点重合时的转换坐标;确定模块,还用于根据坐标转换模块转换的每个单元上当前点群中各个空间点的转换坐标,确定当前点群中各个空间点在垂直于历史基准轴线的平面上的当前投影点坐标,并利用nurbs拟合得到当前投影拟合函数;根据每个单元上历史点群中各个空间点的历史大地坐标,确定历史点群中各个空间点在垂直于历史基准轴线的平面上的历史投影点坐标,并利用nurbs拟合得到历史投影拟合函数;确定模块,还用于确定拟合圆的圆心坐标、拟合圆上指定点的局部坐标、拟合圆上指定点在当前投影拟合函数上的当前最佳投影点坐标,以及在历史投影拟合函数上的历史最佳投影点坐标,其中,所述拟合圆由每个单元上当前点群中各个空间点在与历史基准轴线垂直的平面上的投影点拟合得到;确定模块,还用于根据当前最佳投影点坐标、历史最佳投影点坐标、拟合圆上指定点的局部坐标及拟合圆的圆心坐标确定拟合圆上该指定点处隧道局部变形参数;确定模块,还用于当隧道局部变形参数不等于0时,确定隧道局部发生变形,并将隧道局部变形参数的绝对值确定为隧道变形量。
本申请实施例中,将当前轴线调整为与历史基准轴线平行且中点重合的状态,之后,先确定当前状态下隧道节段上每个单元上当前点群中空间点在垂直于当前轴线的平面上的投影点,并利用nurbs拟合确定投影点在平面上的当前投影拟合函数及当前最佳投影点坐标,并且,还确定历史状态下隧道节段每个单元上历史点群中空间点在垂直于历史基准轴线上的历史投影拟合函数及历史最佳投影点坐标,由于垂直于调整后的当前轴线的平面与垂直于历史基准轴线的平面平行且中点重合,根据当前投影拟合函数、当前最佳投影点坐标、历史投影拟合函数及历史最佳投影点坐标可以确定隧道局部变形参数,该隧道局部变形参数用于表征当前状态下的隧道与历史状态下隧道是否发生的变形。由于nurbs拟合出曲线更为符合投影点的整体形态,与现有技术中直接利用圆或椭圆进行拟合相比,提高了隧道节段的局部变形识别精度。
附图说明
为了更清楚地说明本申请实施例或现有技术中的技术方案,下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本申请的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。在附图中:
图1为本申请实施例中一种移动式扫描的工作原理图;
图2为本申请实施例中一种隧道局部变形识别方法的流程图;
图3为本申请实施例中一种在接缝处切分平面的示意图;
图4为本申请实施例中一种当前轴线确定方法的流程图;
图5为本申请实施例中一种隧道轴线确定方法的原理示意图;
图6为本申请实施例中一种确定有效点的原理示意图;
图7为本申请实施例中一种v(t0)与vt方向存在偏差的示意图;
图8为本申请实施例中一种更新后的节段轴线的示意图;
图9为本申请实施例中前后两次计算得到的节段轴线偏差处于偏差阈值范围之内的轴线示意图;
图10为本申请实施例中隧道轴线确定方法的另一种流程图;
图11为本申请实施例中划分特征点的示意图;
图12为本申请实施例中任意指定点
图13为现有技术中传统的利用圆拟合方法对隧道拟合与本申请实施例中利用nurbs进行样条拟合的对比图;
图14为本申请实施例中一种隧道局部变形识别装置的结构示意图。
具体实施方式
为使本申请实施例的目的、技术方案和优点更加清楚明白,下面结合附图对本申请实施例做进一步详细说明。在此,本申请的示意性实施例及其说明用于解释本申请,但并不作为对本申请的限定。
本申请实施例提供了一种隧道局部变形识别方法,如图2所示,该方法包括步骤201至步骤207:
步骤201、将隧道每个节段划分为多个单元,获取每个单元上当前点群中各个空间点在大地坐标系下的当前大地坐标,以及每个节段的历史基准轴线和每个单元上历史点群中各个空间点的历史大地坐标。
其中,历史基准轴线和历史大地坐标是在历史时期中获取的,例如,在隧道建成之时通过测量获取到的,或者在本次隧道局部变形识别之前任意时期获取的,例如,在当前的5年之前或10年之前等时期获取到的。相应的,本申请实施例中比较当前隧道的状态和获取历史基准轴线的历史时期时隧道的状态,以确定当前隧道相对于获取历史基准轴线的历史时期时的隧道是否发生变形。示例性的,如果历史基准轴线是隧道建成之时获取的,则可以确定当前隧道相对于刚建成时的隧道是否发生变形;如果历史基准轴线是5年前获取的,则可以确定当前隧道相对于5年前的隧道是否发生变形。
可以利用三维激光扫描技术采集待测隧道每个节段上每个单元当前点群中各个空间点以及历史点群中各个空间点的大地坐标。三维激光扫描时,一般将扫描起始点的隧道拱顶点确定为原点,遵循右手法则建立大地坐标系。所建立的大地坐标系中,xoy为水平平面,z轴指示竖向高程,y轴与隧道线路走向一致。三维激光扫描仪自动将采集的待测隧道上每个点的位置信息转换为大地坐标系下的大地坐标,本申请实施例中可以直接获取三维激光扫描仪采集的各个空间点的大地坐标。
需要说明的是,由于空间中包含无数个点,三维激光扫描仪难以获取每个点的大地坐标,而是获取其中一部分点的大地坐标,这样,在不同时间扫描或在多次扫描过程中,三维激光扫描仪扫描得到的空间点不会完全相同。因此,本申请实施例中,将当前三维激光扫描仪扫描到的点的集合称为当前点群,将某个历史时期中扫描得到的点的集合称为历史点群,当前点群和历史点群中包含的空间点不完全相同,可能部分相同,可能全部都不相同。
隧道由多个节段构成,不同节段连接处存在接缝,在本申请实施例中,以一个节段为单位,确定该节段的隧道轴线。相应的,也将三维激光扫描仪采集的隧道点的大地坐标按照其所属节段进行切分,得到待分析节段的所有点的大地坐标。示例性的,图1和图3分别示出了不同节段之间连接接缝,以及在接缝处切分平面的示意图。
本申请实施例中,以移动式扫描数据为例,每个单元的长度以涵盖2~5道螺旋式扫描线,且按照该长度划分时,能够将节段划分为整数个单元为宜。每个单元的长度可以由用户根据实际情况确定,且不同节段单元的长度也可以不同,对于每个单元的长度,在此不做限定。示例性的,图5中以δl标示出了一个节段中的一个单元j。
步骤202、根据每个单元上当前点群中各个空间点的当前大地坐标,确定每个节段的当前轴线。
参阅图4,步骤202具体可以执行为如下步骤2021至步骤2028:
步骤2021、针对每个节段,在节段的拱顶两端各选择一个目标点,根据两个目标点的大地坐标确定初始单位方向矢量。
选择拱顶每个端口处z值最大的点作为目标点。所选择的两个目标点分别为ps(xs,ys,zs)、pe(xe,ye,ze),根据如下公式计算初始单位方向矢量vt:
vt=(xt,yt,zt)=(xe-xs,ye-ys,ze-zs)/s
其中,s为ps至pe向量的模,
步骤2022、在每个单元中心构建与初始单位方向矢量垂直的平面,作为投影平面,将投影平面与初始单位方向矢量的交点作为原点,构建局部坐标系。
设节段划分的单元的总数量为m,每个单元的编号为j,j=1,2,...,m。参见图5,在单元j中心处构建了一个与第一单位方向矢量vt垂直的平面
(xse-j,yse-j,zse-j)=(j-0.5)svt/m+(xs,ys,zs)
投影平面
xt(x-xse-j)+yt(y-yse-j)+zt(z-zse-j)=0
为了便于利用最小二乘法在投影平面
步骤2023、将每个单元上每个点投影到投影平面,将投影到指定范围内的投影点确定为有效点;将有效点的大地坐标转换为局部坐标系下的局部坐标。
参见图6,图6为将一个单元上的每个点投影到投影平面后的投影平面的示意图。图6中示出了局部坐标系的x轴方向和y轴方向。
本申请实施例中,在所有投影点中沿y轴方向选择间距最大的两个点作为纵轴外边缘点,沿x轴方向选择隧道拱顶的一个点作为横轴外边缘点,利用两个纵轴外边缘点和一个横轴外边缘点确定外边界圆,得到外边界圆的圆心和半径;将与外边界圆共圆心,半径小于外边界圆半径预设偏移量的圆确定为内边界圆;将内边界圆和外边界圆构成的圆环确定为指定范围。如图6所示,将落在该内外边界圆环内的投影点作为有效点,其余点视为无效点。其中,隧道壁电气化挂柱、通风管道、交通指示、照明、通讯、装饰物等附属设施及测量系统的不稳定性是导致无效点产生的主要因素。
预设偏移量δd由隧道纵坡及三维激光扫描仪等测量大地坐标的测量系统的测距精度决定,其具体计算方式如下:
δd=α(δl|zt|+2δ)
其中,α表示经验系数,用于线性综合调整隧道纵坡及测量系统精度影响;δl表示单元的长度;|zt|表示第一单位方向矢量的分项绝对值;δ表示隧道大地坐标测量系统的测距精度,也即三维激光扫描仪等测量系统的测距精度。需要说明的是,三维激光扫描仪等测量系统通过测量距离和角度等参数来换算得到大地坐标,一般测量系统中会给出测距精度,因此,此处利用的δ可以直接从三维激光扫描仪等大地坐标测量系统中直接获取到。
每个单元上当前大地坐标为pi的每个空间点投影到投影平面后,其投影点在大地坐标系下的大地坐标
其中,t表示矩阵转置运算;zse-j表示交点pse-j的z轴坐标。
将单元j在平面
(x,y,z)t=r{(x,y,z)t+q}
其中,x、y、z分别表示局部坐标系中的x轴、y轴和z轴的坐标值;x、y、z分别表示大地坐标系中x轴、y轴和z轴的坐标值;r表示由大地坐标系变换至局部坐标系的旋转矩阵;q表示由大地坐标系变换至局部坐标系的平移向量;
具体的,r与q分别根据如下方法计算:
q=[-xse-j-yse-j-zse-j]t
上式中,ux=(uxi,uxj,uxk),uz=(uyi,uyj,uyk),uy=(uzi,uzj,uzk),ux、uy、uz分别为局部坐标系x轴、y轴、z轴在大地坐标系中的单位坐标向量。
因ux与大地坐标系z轴在投影平面
uz=vt=(xt,yt,zt)
uy=uz×ux
计算得到ux、uz、uy后,即可确定r。
步骤2024、利用每个单元的有效点在投影平面上拟合圆,确定拟合圆的圆心局部坐标,将圆心局部坐标转换为圆心大地坐标。
需要说明的是,利用点的坐标及最小二乘法拟合圆,并确定拟合圆的圆心坐标是本领域的常用技术手段,对于其具体过程,在此不做赘述。
将圆心局部坐标转换为大地坐标系下的圆心大地坐标的计算方法为:
(x,y,z)t=r-1(x,y,z)t-q
步骤2025、将每个节段所有单元的圆心大地坐标进行空间直线拟合,得到第一轴线;根据第一轴线确定第一单位方向矢量。
按照步骤2022至步骤2024中的方法可以分别确定节段中每个单元的圆心大地坐标,将所有单元的圆心大地坐标进行空间直线拟合可以得到第一轴线,示例性的,如图5所示,ax(t0)即为由圆心
任意m个空间坐标点拟合空间直线射影式方程,也即第一轴线的参数方程为:
上式中,组建由方程系数构建的待求矩阵:
a=[a1a2]t=(z1z1t)-1z1x1
b=[b1b2]t=(z1z1t)-1z1y1
其中,x1、y1、z1为m个点坐标(x1,y1,z1)、...、(xm,ym,zm)构建的计算元素,构建方法如下:
x1=[x1x2…xm]t,y1=[y1y2…ym]t,
根据上述公式可以确定a1与b1,即可确定第一轴线的方向向量(a1,b1,1)。
则第一单位方向矢量v(t0)的大地坐标(xt0,yt0,zt0)为:
步骤2026、利用根据初始单位方向矢量确定第一轴线和第一单位方向矢量的方法,根据第一单位方向矢量确定每个节段的第二轴线和第二单位方向矢量。
因在节段两端拱顶拾取的目标点ps、pe为人为挑选,与隧道轴线走向可能存在偏差,拟合后节段第二单位方向矢量v(t0)与vt方向存在偏差,如图7所示。
本步骤在于更新节段轴线计算结果。得到v(t0)后,沿v(t0)再次划分单元,每个单元构建新的投影平面
步骤2027、确定第一单位方向矢量与第二单位方向矢量的偏差。
具体的,根据c=1-v(t0)·v(t1)=1-xt0xt1-yt0yt1-zt0zt1确定第一单位方向矢量v(t0)与第二单位方向矢量v(t1)的偏差c。
步骤2028、如果偏差小于等于偏差阈值,则将第二轴线确定为该节段隧道的当前轴线。
步骤2027及步骤2028在于判别更新后的节段轴线与初次计算的节段轴线的吻合(或称为平行)程度,如果两者之间的偏差在偏差阈值的范围之内,则认为两次计算得到的节段轴线相互平行,将第二轴线确定为该节段隧道的隧道轴线。前后两次节段轴线偏差处于限值范围之内,状态如图9所示。
若二者之间存在超过偏差阈值的偏差,参见图10,第二单位方向矢量作为新的第一单位方向矢量,根据新的第一单位方向矢量计算新的第二单位方向矢量和第二轴线,直至极端得到的第一单位方向矢量与第二单位方向矢量的偏差小于等于偏差阈值,将最后一次计算得到的第二轴线确定为该节段隧道的隧道轴线。
隧道的每个节段都按照步骤2022至步骤2027中的方法进行计算,可以得到隧道所有节段的当前轴线。
需要说明的是,如果获取到历史大地坐标,没有获取到历史基准轴线,可以利用上述步骤2021至步骤2028中的方法确定历史基准轴线,将上述步骤2021至步骤2028中使用的各个空间点的当前大地坐标替换为相应的历史大地坐标即可。
上述步骤2021至步骤2028中,通过对隧道每个节段划分单元,将每个单元上的点投影到投影平面上,保留指定范围内的投影点作为有效点,对有效点进行圆拟合确定单元圆心,将划分的多个单元的圆心拟合确定轴线,并通过迭代更新确定隧道节段轴线,可以获得隧道节段的精确轴线,获得的轴线的精度高,适用于隧道运营期变形分析,为隧道的局部变形分析提供基础。
步骤203、调整当前轴线与历史基准轴线平行且当前轴线的中点与历史基准轴线的中点重合,将每个单元上当前点群中各个空间点的大地坐标转换为当前轴线平行于历史基准轴线且当前轴线的中点与历史基准轴线的中点重合时的转换坐标。
考虑到不同状态下采集数据坐标系可能存在差异,为将变形后状态与基准状态进行比对,需将变形后轴线与基准轴线进行叠合,轴线叠合准则为:①维持历史基准轴线不变,调整当前轴线,使调整后的当前轴线与历史基准轴线平行;②将调整后的当前轴线的中点与历史基准轴线的中点重合。为此需要对当前轴线和当前点群中空间点的当前大地坐标进行空间变换,任意一点或向量的变换方法如下:
(x(0),y(0),z(0))t=r1(x(1),y(1),z(1))t+t1
其中,(x(1),y(1),z(1))表示所需转换的空间点的大地坐标;(x(0),y(0),z(0))表示各个空间点的大地坐标对应的转换坐标;r1表示空间旋转矩阵,r1=r(γ)·r(τ)·r(β)。
步骤204、根据每个单元上当前点群中各个空间点的转换坐标,确定当前点群中各个空间点在垂直于历史基准轴线的平面上的当前投影点坐标,并利用nurbs拟合得到当前投影拟合函数;根据每个单元上历史点群中各个空间点的历史大地坐标,确定历史点群中各个空间点在垂直于历史基准轴线的平面上的历史投影点坐标,并利用nurbs拟合得到历史投影拟合函数。
具体的,在每个单元中心建立与历史基准轴线垂直的垂直平面,将每个单元上当前点群中各个空间点投影到垂直平面上,得到当前点群中各个空间点对应的当前投影点;以历史基准轴线与垂直平面的交点为原点,构建局部坐标系,根据当前点群中空间点的转换坐标确定局部坐标系下当前投影点的局部坐标;利用当前投影点拟合圆,根据当前投影点的局部坐标确定拟合圆的圆心和圆心坐标,以拟合圆的圆心为中心,以预设角度为圆心角,将拟合圆划分为多个扇形;根据每个扇形范围内投影点的局部坐标确定每个扇形范围内投影点的特征点,对所有扇形范围内的特征点进行非均匀有理b样条(non-uniformrationalb-splines,nurbs)拟合,得到当前投影拟合函数。
需要说明的是,确定历史投影拟合函数的方法与确定当前投影拟合函数的方法相同,在此不再赘述。
对每个扇形范围内所有投影点的局部坐标求平均值,也即,x轴、y轴、z轴分别求平均值,将得到的平均x坐标、平均y坐标、平均z坐标作为该扇形范围内特征点的局部坐标。
基于特征点开展nurbs拟合,得到拟合函数c(u)的方法如下所示:
上式中p为多项式次数,ωi为权重向量元素。ni,p(u)为基函数方程,具体求解方法如下:
上式中,ui为非均匀单调的节点向量u元素,u定义如下:
节点向量元素个数m+1与多项式次数p及特征点数n+1之间满足以下约束:
m=n+p+1
步骤205、确定拟合圆的圆心坐标、拟合圆上指定点的局部坐标、拟合圆上指定点在当前投影拟合函数上的当前最佳投影点坐标,以及在历史投影拟合函数上的历史最佳投影点坐标。
其中,拟合圆由每个单元上当前点群中各个空间点在与当前轴线垂直的平面上的投影点拟合得到。在拟合时,利用了最小二乘法。
需要说明的是,利用当前点群中空间点的转换坐标确定投影点的局部坐标、利用投影点拟合圆、根据投影点的局部坐标确定拟合圆的圆心和圆心坐标,可以根据步骤2023和步骤2024实现,对于其具体过程,在此不做赘述。
示例性的,图11给出了以拟合圆的圆心为中心,以
设拟合圆半径为r圆,拟合圆的圆心
计算任意指定点
平面任意一点至曲线c(u)的最佳投影点的计算原理方法如下:
①、构建与曲线c(u)关系的函数f(u):
f(u)=c′(u)·(c(u)-p)
②、在(0,1)范围内设定u的初值,开展迭代计算,其中第k+1次与第k次u值计算关系式如下所示:
上式中c′(uk)标识曲线c(u)在uk处的一阶导矢,c″(uk)标识曲线c(u)在uk处的二阶导矢。
③、迭代计算收敛判别准则如下:
基于①②计算公式驱动,在③的约束下,可求得平面任意一点至曲线c(u)的最佳投影点所对应的节点值uopt,将节点值uopt带入曲线c(u)函数即可求得最佳投影点坐标p(u)。
根据上述①~③,可以确定pi在当前投影拟合函数上的当前最佳投影点坐标
步骤206、根据当前最佳投影点坐标、历史最佳投影点坐标、拟合圆上指定点的局部坐标及拟合圆的圆心坐标确定拟合圆上该指定点处隧道局部变形参数。
拟合圆上该指定点pi处隧道局部变形参数δρ根据如下公式进行计算:
其中,
步骤207、如果隧道局部变形参数不等于0,则确定隧道局部发生变形,并将隧道局部变形参数的绝对值确定为隧道变形量。
如果隧道局部变形参数大于0,则确定隧道相对于历史基准轴线对应的历史状态,发生了变形,且变形方向为径向向心;如果隧道局部变形参数小于0,则确定隧道相对于历史基准轴线对应的历史状态,发生了变形,且变形方向为径向离心。并且,δρ的绝对值为隧道变形量,也即隧道变形的大小,δρ的绝对值越大,隧道变形越大。
参见图13,为传统的利用圆拟合方法对隧道拟合与本申请实施例中利用nurbs进行样条拟合的对比图,其中,基准状态圆拟合、变形后圆拟合分别为利用传统的利用圆或椭圆断面拟合方法对历史状态和当前状态隧道拟合后得到的拟合曲线,基准状态
本申请实施例中,将当前轴线调整为与历史基准轴线平行且中点重合的状态,之后,先确定当前状态下隧道节段上每个单元上当前点群中空间点在垂直于当前轴线的平面上的投影点,并利用nurbs拟合确定投影点在平面上的当前投影拟合函数及当前最佳投影点坐标,并且,还确定历史状态下隧道节段每个单元上历史点群中空间点在垂直于历史基准轴线上的历史投影拟合函数及历史最佳投影点坐标,由于垂直于调整后的当前轴线的平面与垂直于历史基准轴线的平面平行且中点重合,根据当前投影拟合函数、当前最佳投影点坐标、历史投影拟合函数及历史最佳投影点坐标可以确定隧道局部变形参数,该隧道局部变形参数用于表征当前状态下的隧道与历史状态下隧道是否发生的变形。由于nurbs拟合出曲线更为符合投影点的整体形态,与现有技术中直接利用圆或椭圆进行拟合相比,提高了隧道节段的局部变形识别精度。
本申请实施例中还提供了一种隧道局部变形识别装置,如图14所示,该装置1400包括获取模块1401、确定模块1402和坐标转换模块1403。
获取模块1401,用于将隧道每个节段划分为多个单元,获取每个单元上当前点群中各个空间点在大地坐标系下的当前大地坐标,以及每个节段的历史基准轴线和每个单元上历史点群中各个空间点的历史大地坐标。
确定模块1402,用于根据获取模块1401获取的每个单元上当前点群中各个空间点的当前大地坐标,确定每个节段的当前轴线。
坐标转换模块1403,用于调整确定模块1402确定的当前轴线与获取模块1401获取的历史基准轴线平行且当前轴线的中点与历史基准轴线的中点重合,将每个单元上当前点群中各个空间点的大地坐标转换为当前轴线平行于历史基准轴线且当前轴线的中点与历史基准轴线的中点重合时的转换坐标。
确定模块1402,还用于根据坐标转换模块1403转换的每个单元上当前点群中各个空间点的转换坐标,确定当前点群中各个空间点在垂直于历史基准轴线的平面上的当前投影点坐标,并利用nurbs拟合得到当前投影拟合函数;根据每个单元历史点群中各个空间点的历史大地坐标,确定历史点群中各个空间点在垂直于历史基准轴线的平面上的历史投影点坐标,并利用nurbs拟合得到历史投影拟合函数。
确定模块1402,还用于确定拟合圆的圆心坐标、拟合圆上指定点的局部坐标、拟合圆上指定点在当前投影拟合函数上的当前最佳投影点坐标,以及在历史投影拟合函数上的历史最佳投影点坐标,其中,所述拟合圆由每个单元上当前点群中各个空间点在与历史基准轴线垂直的平面上的投影点拟合得到。
确定模块1402,还用于根据当前最佳投影点坐标、历史最佳投影点坐标、拟合圆上指定点的局部坐标及拟合圆的圆心坐标确定拟合圆上该指定点处隧道局部变形参数。
确定模块1402,还用于当隧道局部变形参数不等于0时,确定隧道局部发生变形,并将隧道局部变形参数的绝对值确定为隧道变形量。
在本申请实施例的一种实现方式中,坐标转换模块1403,用于:
根据(x(0),y(0),z(0))t=r1(x(1),y(1),z(1))t+t1确定当前点群中各个空间点的大地坐标(x(1),y(1),z(1))对应的转换坐标(x(0),y(0),z(0));
其中,r1表示空间旋转矩阵,r1=r(γ)·r(τ)·r(β),
在本申请实施例的一种实现方式中,确定模块1402,用于:
在每个单元中心建立与历史基准轴线垂直的垂直平面,将每个单元上当前点群中各个空间点投影到垂直平面上,得到当前点群中各个空间点对应的当前投影点;
以历史基准轴线与垂直平面的交点为原点,构建局部坐标系,根据当前点群中空间点的转换坐标确定局部坐标系下当前投影点的局部坐标;
利用当前投影点拟合圆,根据当前投影点的局部坐标确定拟合圆的圆心和圆心坐标,以拟合圆的圆心为中心,以预设角度为圆心角,将拟合圆划分为多个扇形;
根据每个扇形范围内投影点的局部坐标确定每个扇形范围内投影点的特征点,对所有扇形范围内的特征点进行nurbs拟合,得到当前投影拟合函数。
在本申请实施例的一种实现方式中,确定模块1402,用于:
计算每个扇形范围内所有投影点的局部坐标的平均值,将计算得到的平均值对应的点作为每个扇形范围内投影点的特征点。
在本申请实施例的一种实现方式中,指定点为拟合圆上划分的扇形的角平分线与拟合圆的交点;确定模块1402,用于:
根据
其中,(xo,yo)表示拟合圆的圆心坐标;r圆表示拟合圆的半径;i表示划分的第i个扇形;
在本申请实施例的一种实现方式中,确定模块1402,用于:
根据
其中,
在本申请实施例的一种实现方式中,确定模块1402,用于
针对每个节段,在节段的拱顶两端各选择一个目标点,根据两个目标点的大地坐标确定初始单位方向矢量;
在每个单元中心构建与初始单位方向矢量垂直的平面,作为投影平面,将投影平面与初始单位方向矢量的交点作为原点,构建局部坐标系;
将每个单元上每个点投影到投影平面,将投影到指定范围内的投影点确定为有效点;将有效点的大地坐标转换为局部坐标系下的局部坐标;
利用每个单元的有效点在投影平面上拟合圆,确定拟合圆的圆心局部坐标,将圆心局部坐标转换为圆心大地坐标;
将每个节段所有单元的圆心大地坐标进行空间直线拟合,得到第一轴线;根据第一轴线确定第一单位方向矢量;
利用根据初始单位方向矢量确定第一轴线和第一单位方向矢量的方法,根据第一单位方向矢量确定每个节段的第二轴线和第二单位方向矢量;
确定第一单位方向矢量与第二单位方向矢量的偏差;
如果所述偏差小于等于偏差阈值,则将第二轴线确定为该节段隧道的当前轴线。
在本申请实施例的一种实现方式中,两个目标点分别为ps(xs,ys,zs)、pe(xe,ye,ze),确定模块1402,用于:
根据vt=(xt,yt,zt)=(xe-xs,ye-ys,ze-zs)/s计算第一单位方向矢量vt;
其中,s为ps至pe向量的模,
在本申请实施例的一种实现方式中,确定模块1402,用于:
将投影平面与初始单位方向矢量的交点作为局部坐标系的原点,将大地坐标系中x轴方向作为局部坐标系的y轴方向,将大地坐标系中指向竖向高程的z轴在投影平面上投影的反方向作为局部坐标系的x轴方向,将初始单位方向矢量的方向作为局部坐标系的z轴方向,构建局部坐标系。
在本申请实施例的一种实现方式中,确定模块1402,还用于
在所有投影点中沿y轴方向选择间距最大的两个点作为纵轴外边缘点,沿x轴方向选择隧道拱顶的一个点作为横轴外边缘点,利用两个纵轴外边缘点和一个横轴外边缘点确定外边界圆,得到外边界圆的圆心和半径;
根据δd=α(δl|zt|+2δ)确定预设偏移量δd;其中,α表示经验系数;δl表示单元的长度;|zt|表示初始单位方向矢量的分项绝对值;δ表示隧道大地坐标测量系统的测距精度。
将与外边界圆共圆心,半径小于外边界圆半径预设偏移量的圆确定为内边界圆;
将内边界圆和外边界圆构成的圆环确定为指定范围。
在本申请实施例的一种实现方式中,确定模块1402,还用于:
根据(xse-j,yse-j,zse-j)=(j-0.5)svt/m+(xs,ys,zs)确定交点pse-j的坐标(xse-j,yse-j,zse-j);
其中,j表示划分的第j个单元,j=1,2,...,m,m表示节段划分的单元的总数量。
确定模块1402,用于:
根据
利用(x,y,z)t=r{(x,y,z)t+q}的原理,将有效点大地坐标转化为局部坐标;
其中,pi表示第i个有效点对应的单元上空间点的大地坐标;vt表示初始单位方向矢量;t表示矩阵转置运算;zse-j表示交点pse-j的z轴坐标;x、y、z分别表示局部坐标系中的x轴、y轴和z轴的坐标值;x、y、z分别表示大地坐标系中x轴、y轴和z轴的坐标值;r表示由大地坐标系变换至局部坐标系的旋转矩阵;q表示由大地坐标系变换至局部坐标系的平移向量;
其中,
在本申请实施例的一种实现方式中,确定模块1402,用于:
构建第一轴线的参数方程
根据[a1a2]t=(z1z1t)-1z1x1,[b1b2]t=(z1z1t)-1z1y1确定参数方程的待求参数a1、a2、b1、b2;其中,x1=[x1x2…xm]t,y1=[y1y2…ym]t,
根据
在本申请实施例的一种实现方式中,确定模块1402,用于:
根据c=1-v(t0)·v(t1)=1-xt0xt1-yt0yt1-zt0zt1确定第一单位方向矢量v(t0)与第二单位方向矢量v(t1)的偏差c,其中,(xt1,yt1,zt1)为第二单位方向矢量v(t1)的大地坐标。
在本申请实施例的一种实现方式中,确定模块1402,还用于:
如果所述偏差大于偏差阈值,则将第二单位方向矢量作为新的第一单位方向矢量,根据新的第一单位方向矢量计算新的第二单位方向矢量和第二轴线,直至计算得到的第一单位方向矢量与第二单位方向矢量的偏差小于等于偏差阈值,将最后一次计算得到的第二轴线确定为该节段隧道的隧道轴线。
本申请实施例中,将当前轴线调整为与历史基准轴线平行且中点重合的状态,之后,先确定当前状态下隧道节段上每个单元上当前点群中空间点在垂直于当前轴线的平面上的投影点,并利用nurbs拟合确定投影点在平面上的当前投影拟合函数及当前最佳投影点坐标,并且,还确定历史状态下隧道节段每个单元上历史点群中空间点在垂直于历史基准轴线上的历史投影拟合函数及历史最佳投影点坐标,由于垂直于调整后的当前轴线的平面与垂直于历史基准轴线的平面平行且中点重合,根据当前投影拟合函数、当前最佳投影点坐标、历史投影拟合函数及历史最佳投影点坐标可以确定隧道局部变形参数,该隧道局部变形参数用于表征当前状态下的隧道与历史状态下隧道是否发生的变形。由于nurbs拟合出曲线更为符合投影点的整体形态,与现有技术中直接利用圆或椭圆进行拟合相比,提高了隧道节段的局部变形识别精度。
本申请实施例还提供了一种计算机设备,包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序,处理器执行计算机程序时实现步骤201至步骤207及其各种实现方式所述的任一方法。
本申请实施例还提供了一种计算机可读存储介质,计算机可读存储介质存储有执行步骤201至步骤207及其各种实现方式所述的任一方法的计算机程序。
本领域内的技术人员应明白,本申请的实施例可提供为方法、系统、或计算机程序产品。因此,本申请可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且,本申请可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、小型光盘只读存储(compactdiskreadonlymemory,cd-rom)、光学存储器等)上实施的计算机程序产品的形式。
本申请是参照根据本申请实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器,使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中,使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品,该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上,使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理,从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。
以上所述的具体实施例,对本申请的目的、技术方案和有益效果进行了进一步详细说明,所应理解的是,以上所述仅为本申请的具体实施例而已,并不用于限定本申请的保护范围,凡在本申请的精神和原则之内,所做的任何修改、等同替换、改进等,均应包含在本申请的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!