一种高考选科模型及其建立方法与流程

本发明涉及计算机领域，更确切地说是一种高考选科模型及其建立方法。
背景技术：
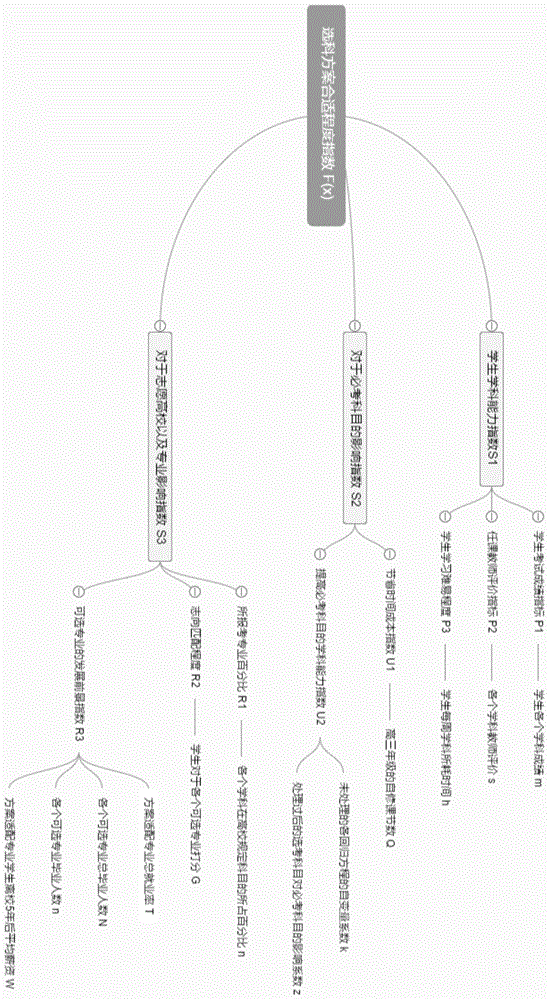
：2014年9月19日，发布的《全国深化高等学校考试招生综合改革实施方案(以上海、浙江为试点地区)》，简称2017上海市“3+3”新高考改革方案。文件中提及，上海地区将于2017年作为试点地区正式实行“3+3”模式，并且将于2019年开始全国推广。作为新高考的第三届考生，都存在着对于加三的“选科难”问题，究竟该依据什么来从物理，化学，生物，政治，历史，地理中选出自己将要面对参加高考的三门课程那？于是，通过对603名来自上海市不同学校的初三，高一，高二学生的问卷调查，发现他们在选科时大多都会被以下三点所左右①学生本人六门选考科目水平②选考科目对于“3+3”整体的影响。(其中包括每门学科花费时间，教师的建议评价，对于必考科目的影响等等)③选考科目对志愿高校及专业填报的影响。那么，能否利用层次分析法建立一种选科模型，使其能帮助同学们在选科时，只需将自己的学习成绩，每门学科花费时间，理想高校以及专业等一系列基本信息量化输入后，就能轻松的得到自己最适合的+3选科呢？本课题将通过线性回归结合层次分析来做出一个建立在excel上的选科工具，使其能根据同学们的个人学习情况为新高考20种选科组合进行个性化的私人专属“打分”，以为其量身打造出最合适的选科。如果该课题成功，将会为许多高中的“选科难”问题提供一个很有价值的参考，无疑是新高考体制下，对于许多同学们的一大福音。技术实现要素：本发明的目的是提供一种高考选科模型及其建立方法，其可以解决现有技术中的上述缺点。本发明采用以下技术方案：一种高考选科模型建立方法，包括：建立一选科方案合适程度指数f(x)，其中，s1为学生学科能力指数；s2为对于必考科目的影响指数；s3为对于志愿高校及专业影响指数。s1学生学科能力指数具体还包括：学生考试成绩指标p1、任课教师评价指标p2、学生学习难易程度指标p3。s2对于必考科目的影响指数具体还包括：节省时间成本指标u1、提高必考科目的学科能力指数u2。s3对于志愿高校及专业影响指数还包括：选科方案适配专业所占百分比r1、志向匹配程度指标r2、可选专业的发展前景指数r3。可选专业的发展前景指数r3指数还包括方案适配专业总就业率t、各个可选专业总毕业人数n、各个可选专业毕业人数n,方案适配专业学生离校5年后平均薪资w。一种高考选科模型，包括：该模型包括一选科方案合适程度指数f(x)，其中，s1为学生学科能力指数；s2为对于必考科目的影响指数；s3为对于志愿高校及专业影响指数。s1学生学科能力指数具体还包括：学生考试成绩指标、任课教师评价指标、学生学习难易程度指标。s2对于必考科目的影响指数具体还包括：节省时间成本指标、提高必考科目的学科能力指数。s3对于志愿高校及专业影响指数还包括：选科方案适配专业所占百分比r1、志向匹配程度指标r2、可选专业的发展前景指数r3。可选专业的发展前景指数r3指数还包括方案适配专业总就业率t、各个可选专业总毕业人数n、各个可选专业毕业人数n,方案适配专业学生离校5年后平均薪资w。本发明的优点是：将笼统的结论具体化、科学化是本发明的一大创新之处；选考科目对于提高必考科目学科水平的帮助，并引入线性回归分析得到各个选考科目对于必考科目的影响系数以及标准化处理过后的变量系数和学生的各科分数，提出了一个新的研究方面和思考方法；通过利用计算机进行计算，促使计算结果更加迅速，应用前景更加广泛。附图说明图1是本发明的结构示意图。图2是实施例1的结构示意图。图3是本发明中的学生学科能力评价模型体系示意图。图4是本发明中的对于必考科目的影响评判模型体系的示意图。图5是本发明中的必考科目的模型示意图。图6至图11是本发明中的必考科目中的各学科的关系示意图。图12是本发明的传统文科的回归标准化的正态p-p图。图13是本发明的传统理科的回归标准化的正态p-p图。图14是本发明中的对于志愿高校以及专业影响模型体系的示意图。具体实施方式下面进一步阐述本发明的具体实施方式：权重表示的是每个因素对于目标影响的程度大小，也就是重要性.因素对目标越重要权重数越大，反之则越小.每位学生在各个因素上能力、水平不同，把这些条件都量化为分值，分别乘以相应权重再相加，得出的最终数值f(x)即是衡量选科方案合适程度的分数。具体到学生，老师对于个人选科的思考产生，可能会和下述若干因素有关：学生考试成绩，任课教师评价，学生每周学科所耗时间，高三自修课节数，各个学科在高校规定科目所占百分比，学生对于各个专业的志向匹配程度，选科组合对应专业的就业率，选科组合对应专业学生离校5年后平均薪资等等。参考高考选科研究以及其他择优方案指标类似研究的文献，最终得到确定学生高考选科的各项指标并建立学生选科方案合适程度指标体系，入图1所示。对于上述指标的详细解释及其分值的确定规则如下：1学生考试成绩指标p1：学生测试成绩是可以直观的反映该学生是否适合该选科组合的首要条件。但为了消除各个学科由于试卷难度差异而导致分数“含金量”的差异，并且遵循新高考选科的“等级考计分方式”在计算该指标时，本发明对学生的成绩进行了统一的标准化处理，确保计算该指标时，能够切实地体现出选科组合为学生带来的实际效益。2任课教师评价指标p2：学校内的老师对学生的学习情况，水平以及能力有着充分的了解，并且也有足够的经验为学生的选科进行指点。故而，他们的打分对于学生的选科而言起着不小的作用。本指标主要是参考教师的打分。3学生学习难易程度指标p3：设想一个学生在某个学科上，耗费了极大的时间，精力和财力才能取得较为满意的成绩，那么他在对于这门学科的选择务必要考虑慎重。因为在高三，备战高考的重要阶段，多门课程学业压力繁重，倘若学生在一门课程上耗费了大量的时间，那么必然会影响到学生个人整体的学习心态和效率。为了尽量避免考生在选科以后，出现类似状况，本指标将通过参考学生每周在学科上所耗费的时间来量化体现。4节省时间成本指标u1：因为在新高考体制下，生物，地理两门课的课程大纲相对另外四门课(物理，化学，政治，历史)而言，被精简得较多，因而被允许在高二就进行高考。所以，若报考这两门课，会为学生在高三的校内学习生活带来更多自由支配的时间，学生可以以此来制定更合适的复习计划，本指标将着重参考统计出的学生因选科而空闲出的高三学习时间。5提高必考科目的学科能力指数u2：在传统对学科特性的认知中，物理、化学、生物为理科，政治、历史、地理为文科，尽管这样的思维联系在近年来的高考模式中的体现出现得越来越少了，但至少还能体现出一些选科对于必考科目(语文、数学)学习能力的影响，对于物理、化学学科的素养提升，思维拓展，在一定程度上，必然可以强化数学学科的综合能力，助他们在数学考试中披荆斩棘；而文科方面，政治，历史学科的学习可以在潜移默化的过程中熏陶他们的人文情怀，让学生在语文的考场上得心应手。本指标将利用ibmspss软件，建立多元线性回归方程，通过对其各个科目前代表的系数的百分化和均值化处理，来反映各学科对于必考科目的影响程度，由于我国普通高中均用中文进行非外语科目的教学，故各个选科对于外语科目无法起到什么影响，忽略不计。6选科方案适配专业所占百分比r1：建立这一指标能够直观地体现出选科方案对于专业填报的优势，许多知名高校的知名专业为了确保录取学生的专业能力，从6门选考科目中选取了一至两门作为报考该专业的必选科目.本因素可用该选课方案可报考专业的占比来表示.(注：本指标中只考虑北京大学、清华大学、复旦大学、上海交通大学、浙江大学、同济大学、上海市财经大学、上海市外国语大学、华东师范大学、东华大学、华东理工大学、上海大学十二所高校的专业)值得注意的是，一些专业对选取科目有着一些其他要求.例如北京大学化学系规定的必选科目只有化学一门，但备注为“同等条件下优先录取物理考生”。这样的情况在全国的高校中并非个例.虽然报考该专业的考生并非一定选考物理，但选考物理会给考生带来一定优势.建立本指标时将对此情况进行处理，提高模型的实用性、准确性。7志向匹配程度指标r2：学生通过高考的选拔进入高校及其专业来深入地学习知识，实现自我从初等科学向高等科学的转型，成为一个能够报效社会、国家发展的栋梁之才。但这前提应该是，进入自我理想的、志趣相投的高校及其专业，这样学生才会有充沛的动力和不竭的兴趣。不同于其它指标，本指标将通过让学生自行客观打分来反映该因素。8可选专业的发展前景指数r3：不同的高校及其专业有不同的发展空间.一些专业在就业时会受到青睐，而有的专业由于应用性和知名度较低，在就业时会被许多企业忽视。不少人将这一方面作为选择专业的重要考量依据.本模型中将使用毕业生离校1年后就业率和毕业生离校5年后薪资待遇反映这一指标。本发明利用层次分析法建立一种选科模型，使其能帮助同学们在选科时，只需将自己的学习成绩，每门学科花费时间，理想高校以及专业等一系列基本信息量化输入后，就能轻松的得到自己最适合的选科呢，本发明将通过线性回归结合层次分析来做出一个建立在excel上的选科工具，使其能根据同学们的个人学习情况为新高考20种选科组合进行个性化的私人专属“打分”，以为其量身打造出最合适的选科。本发明具有以下优点：(1)目前所能查阅到的关于帮助学生自主选取科目的文献几乎都是定性研究，根据调查分析等研究得出的笼统结论，但却没有定量的研究，.将笼统的结论具体化、科学化是本发明的一大创新之处.(2)本发明考虑选考科目对于提高必考科目学科水平的帮助，并引入线性回归分析得到各个选考科目对于必考科目的影响系数以及标准化处理过后的变量系数和学生的各科分数，提出了一个新的研究方面和思考方法；.(3)通过利用计算机进行计算，促使计算结果更加迅速，应用前景更加广泛。实施例1以下截取上海市某示范性高中某班某次期末大考经排名后的成绩(原始分数)，样本容量为50。如表1所示，表1将上述原始分数，通过本模型的标准化处理过后，得到了如表2所示的成绩(标准分数)以及排名：表2如图2所示，建立模型体系，本发明中采用层次分析法传统的1～9的尺度来衡量两两因素之间的重要性比较：如图3所示，表3通过上式构造矩阵如表4所示：表4经过一致性检验并且归一化并保留四位小数后可得，如表5所示，选科方案合适程度模型权重满分s10.22912291s20.64876487s30.12221222表5可列得以下算式：(s1)max＝2291(s2)max＝6487(s3)max＝1222得到检验模型，如表6所示，表6可以得到四位同学的选科方案的总得分，如表7所示：学生编号适合程度总分18443.528425.538159.547243表7本发明同四位同学及部分家长、老师进行交流，他们均认为该项分数高低能够真实地反映四种选科方案的适合程度，说明了本模型的合理性.如图3所示，其为学生学科能力评价模型，模型体系。同理，运用层次分析法，对于学科水平构造对比矩阵，如表8所示，表8经过计算可得：ci＝0.003cr＝5.17×10-3＜0.1，故该矩阵同样通过一致性检验.进一步计算，可求得权重，如表9所示：表9整理后得到如下公式：检验模型，如表10所示，科目1科目2科目31819479292798437092714928292表10本发明从教师处获取相关数据，将四人的成绩标准化处理后，得到下列结查，如表11所示，科目1科目2科目3总分10.807411.607990.04793249.26621.923660.780430.05083255.09843-0.308841.30847-1.54900189.012641.283931.082611.03537268.0382表11本次考试标准化后的最高总分为278.316，故可计算得到四人在“成绩”因素中的得分(保留整数)，如表12所示，表12本发明在询问各科任教教师后，得到教师对四位同学的评分：学生编号教师评分1教师评分2教师评分317.598297.57.536.59748.57.58表13故可计算得到四位同学在“教师评价”因素上的分数(保留整数)：学生编号“教师评价”因素得分1429242033944420表14本发明在调查四位同学后，得到他们在各学科花费的时间.根据本发明自身经验，一般一周内的校内自由支配时间为5.5小时.故可计算得到四位同学在“学科所耗时间”因素上所得分数(保留整数)：学生编号所耗时间(小时)“学科所耗时间”因素得分1312723127347643.5101表15由此得到四位同学“学科水平能力”的分数为：学生编号“学科水平能力”得分11886219093147941952表16以上四位同学以及部分家长、老师均认为以上分数能够真实地反映四位同学在相应科目上的学科水平，从一定程度上说明了该模型的合理性.对于必考科目的影响评判模型，如图4所示，其为本发明必考科目的影响评判模型体系图。建立模型由于多余的自由支配的复习时间更能够给学生复习必考科目带来帮助，故给“节省时间成本”因素赋分733分(占比60％)，给“对必考科目影响”因素赋分489分(占比40％).对于节省的时间成本，可得如下公式：如图5所示，由于在必考科目中，文科的数目(语文，英语2门)比理科(数学，1门)多.其中，语文受“+3”文科科目的影响较大，英语受影响较小.根据统计调查，物理、化学、生物对数学学科产生的影响依次递减；历史、政治、地理对于语文、英语学科的影响同样依次递减.由于中国普通高中均用中文进行以上“+3”科目的教学，故“+3科目”对于英语科目的影响可以忽略不计。其结果如图6-11所示。由以上图像可知，传统文科中，历史对于语文的影响最大，政治次之；化学对于数学的影响居于传统理科之首，第二是物理。而地理对于语文的影响以及生物对于数学的影响并不明显，故在本模型中将忽略不计地理、生物的影响.本发明利用ibmspss软件，建立多元线性回归模型以得到相应方程.1、传统文科，如表17所示，表17表18表19如图12所示，由此得到回归方程：y＝38.664+0.350x1+0.141x2，其中x1、x2分别代表了学生的历史、政治成绩。2、传统理科表20表21表22如图13所示，由上述数据可求得该回归方程为：y＝44.235+0.138x3+0.344x4，本模型中将各科成绩前的系数作为各学科对必考科目的影响程度的反映.对于每个系数，作出了如下的处理：其中其中t∈{3,4}经过计算后，并保留4位小数得到如下表格：表23地理、生物因在高二时就结束了所有相关课程以及考试，故影响系数赋为0)并得到如下公式：u2＝(zt1+zt2+zt3)×489s3＝u1+u2检验模型如表24所示，本发明抽样了四位同学的选科组合，能够得到这些同学在高三各自能拥有的自修课节数，由此计算到他们在“节省时间成本”指标上的得分：学生编号高三年级自修课节数得分12366.522366.532366.544733表24根据四位同学的选科组合，可得到他们选考科目对于必考科目的影响因素，并计算得到他们在此指标上的得分，如表25所示。学生编号对必考科目影响系数得分10.5244.520.5244.530.4996244.340.3668179.3表25再计算出，四位同学在本指标上的总得分，如表26所示：学生编号“对必考科目影响”总分1611261136104912表26对于志愿高校以及专业影响模型体系如图14所示。建立模型，如表27所示。表27计算得到：ci＝7.7×10-3cr＝0.014＜0.1，故该矩阵具有令人满意的一致性，通过检验.经过归一化处理后可得，如表28所示：对于志愿高校以及专业影响模型权重对应分数r10.5743724r20.3282128r30.098635表28其中，针对“适配专业百分比”指标，遵循以下法则：由于加选理科在适配专业覆盖率上相比文科有巨大的优势。故当选课方案，中同时包括物理、化学时，该指标得分在同等条件下，加50分，以此来量化理科生的选科优势。而对于影响专业发展前景的因素，本发明构造出了如表29所示的矩阵：表29计算得到：ci＝0,cr＝0，故该矩阵通过一致性检验如表30所示，经过归一化处理后，并保留到千分位可得：影响因素权重对应分数离校1年后就业率0.200127离校5年后薪资0.800508表30总结以后可得：其中n为可选专业总数检验模型如表31所示，学生编号可报考专业占比“可报考专业占比”因素得分196.21％3633296.21％3633395.45％3555457.58％2144表31本发明通过向这四位同学展示他们的可选专业，并请他们打分，进一步计算出他们在“志向匹配程度”上面的得分，如表32所示。学生编号学生打分“志向匹配程度”因素得分1919152919153102128491915表32本发明在中国知网上检索有关资料，并不能够收集到所有专业的就业率和薪资，所以在对本模型的检验过程中，采用四位同学个人填报的第一志愿的就业率和薪资作为数据比较的首要依据，数据结果如表33和表34所示。学生编号第一志愿专业(类)就业率薪资待遇(元)1化学工程与工艺93.42％155762应用数学90.55％138363历史88.62％117984环境科学92.10％10751表33表34故可以得到如下四位同学的选科方案在“对于志愿高校以及专业选取的影响”模型上所得分数，如表35所示：学生编号s315999259583604744406表35本发明同四位同学进行了反馈，他们均认为该项分数高低能够真实地反映他们的选科方案在志愿高校以及专业选取上所带来的优势，说明了本模型的合理性。以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。当前第1页12