起落架的可靠性分析方法与流程

本公开涉及可靠性分析技术领域，尤其涉及一种起落架的可靠性分析方法。

背景技术：

作为飞机的关键子系统，起落架系统对飞机的起飞与着陆具有重要的影响。

起落架系统包括起落架支柱和收放机构。该收放机构用于驱动起落架支柱进行收放运动。由于现代飞机使用频率高，服役环境复杂，因而对起落架系统可靠性提出了极高要求和严苛考验。然而，现有技术缺乏对起落架进行可靠性分析的方法。

需要说明的是，在上述背景技术部分公开的信息仅用于加强对本公开的背景的理解，因此可以包括不构成对本领域普通技术人员已知的现有技术的信息。

技术实现要素：

本公开的目的在于提供一种起落架的可靠性分析方法，能够对起落架进行可靠性分析。

根据本公开的一个方面，提供一种起落架的可靠性分析方法，所述起落架包括起落架支柱以及用于驱动所述起落架支柱进行收放运动的收放机构，所述起落架的可靠性分析方法包括：

确定所述收放机构的磨损增量；

根据所述收放机构的磨损增量对所述起落架进行可靠性分析。

在本公开的一种示例性实施例中，根据所述收放机构的磨损增量对所述起落架进行可靠性分析包括：

确定所述起落架的失效模式；

根据所述失效模式和所述收放机构的磨损增量对所述起落架进行可靠性分析。

在本公开的一种示例性实施例中，所述失效模式包括卡滞失效模式、定位失效模式以及精度失效模式中的一种或多种。

在本公开的一种示例性实施例中，所述失效模式包括卡滞失效模式，根据所述失效模式和所述收放机构的磨损增量对所述起落架进行可靠性分析包括：

根据所述收放机构的磨损增量确定g1(x)，所述g1(x)为所述收放机构能提供的最大推力减去所述起落架支柱进行收放运动所需的驱动力的值；

若所述g1(x)小于零，则判定所述起落架失效。

在本公开的一种示例性实施例中，所述失效模式包括定位失效模式，根据所述失效模式和所述收放机构的磨损增量对所述起落架进行可靠性分析包括：

根据所述收放机构的磨损增量确定g2(x)，所述g2(x)为所述起落架支柱的收放运动能达到的最大角度减去所述起落架支柱的收放运动所需的最大角度的值；

若所述g2(x)小于零，则判定所述起落架失效。

在本公开的一种示例性实施例中，所述失效模式包括精度失效模式，根据所述失效模式和所述收放机构的磨损增量对所述起落架进行可靠性分析包括：

根据所述收放机构的磨损增量确定g3(x)，所述g3(x)为所述起落架支柱在最终放下时产生的角度差减去所述起落架支柱在最终放下时所允许的角度差；

若所述g3(x)小于零，则判定所述起落架失效。

在本公开的一种示例性实施例中，确定所述收放机构的磨损增量包括：

确定所述收放机构在一次收放运动中的平均磨损增量；

确定所述起落架支柱的收放运动的次数；

根据所述平均磨损增量与所述收放运动的次数确定所述收放机构的磨损增量。

在本公开的一种示例性实施例中，所述收放机构包括铰链结构，确定所述收放机构在一次收放运动中的平均磨损增量包括：

确定所述铰链结构在一次收放运动中的平均磨损增量，并作为所述收放机构在一次收放运动中的平均磨损增量。

在本公开的一种示例性实施例中，所述铰链结构包括能够相对转动的两个部件，确定所述铰链结构在一次收放运动中的平均磨损增量包括：

根据第一预设关系式确定所述铰链结构在一次收放运动中的平均磨损增量，所述第一预设关系式为：

其中，h为平均磨损增量，t为所述起落架支柱进行一次收放运动所需要的时间，k为磨损系数，p为所述铰链结构中两个所述部件的接触点应力，v为所述铰链结构中两个所述部件的相对转动速度。

在本公开的一种示例性实施例中，所述磨损增量服从正态分布。

本公开的起落架的可靠性分析方法，首先确定收放机构的磨损增量，接着根据收放机构的磨损增量对起落架进行可靠性分析，从而提高了可靠性分析的准确性。

应当理解的是，以上的一般描述和后文的细节描述仅是示例性和解释性的，并不能限制本公开。

附图说明

通过参照附图来详细描述其示例性实施例，本公开的上述和其它特征及优点将变得更加明显。显而易见地，下面描述中的附图仅仅是本公开的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

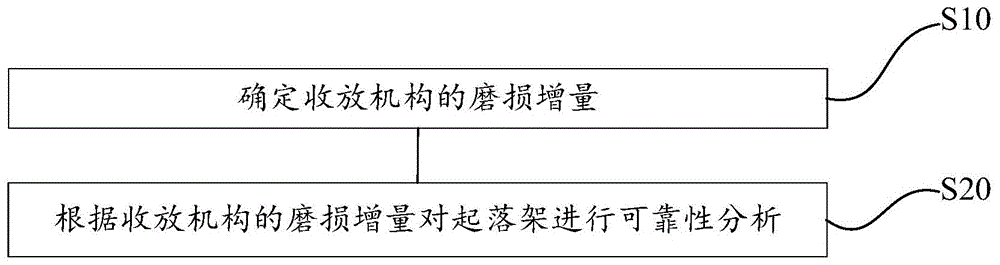
图1为本公开实施方式的起落架的可靠性分析方法的流程图；

图2为本公开实施方式的起落架的可靠性分析方法中步骤s10的流程图；

图3为本公开实施方式的起落架的可靠性分析方法中步骤s20的流程图。

具体实施方式

现在将参考附图更全面地描述示例实施方式。然而，示例实施方式能够以多种形式实施，且不应被理解为限于在此阐述的范例；相反，提供这些实施例使得本公开将全面和完整，并将示例实施例的构思全面地传达给本领域的技术人员。所描述的特征、结构或特性可以以任何合适的方式结合在一个或更多实施方式中。在下面的描述中，提供许多具体细节从而给出对本公开的实施方式的充分理解。然而，本领域技术人员将意识到，可以实践本公开的技术方案而没有所述特定细节中的一个或更多，或者可以采用其它的方法、材料等。在其它情况下，不详细示出或描述公知技术方案以避免模糊本公开的各方面。

此外，用语“一”和“该”用以表示存在一个或多个要素/组成部分/等；用语“包括”和“具有”用以表示开放式的包括在内的意思并且是指除了列出的要素/组成部分/等之外还可存在另外的要素/组成部分/等。

相关技术中，收放机构使起落架发生故障概率较高的部件。在对起落架进行可靠性分析时，分析人员没有考虑到收放机构的磨损增量，降低了可靠性分析的准确性。

为了解决上述问题，本公开实施方式提供一种起落架的可靠性分析方法。该起落架包括起落架支柱以及用于驱动起落架支柱进行收放运动的收放机构。如图1所示，该起落架的可靠性分析方法可以包括：

步骤s10、确定收放机构的磨损增量。

步骤s20、根据收放机构的磨损增量对起落架进行可靠性分析。

本公开实施方式的起落架的可靠性分析方法，首先确定收放机构的磨损增量，接着根据收放机构的磨损增量对起落架进行可靠性分析，从而提高了可靠性分析的准确性。

下面对本公开实施方式的各步骤进行详细说明：

在步骤s10中，确定收放机构的磨损增量。

该磨损增量可以服从正态分布。如图2所示，步骤s10可以包括：

步骤s100、确定收放机构在一次收放运动中的平均磨损增量。

其中，该收放运动为上述起落架支柱的收放运动。该起落架支柱的收放运动为：在飞机降落过程中，该收放机构驱动起落架支柱放下，以使飞机可以着陆；在飞机起飞后，该收放机构驱动起落架支柱收起。其中，飞机经历一次起飞和降落过程，该起落架支柱便进行一次收放运动。

该收放机构可以包括铰链结构。其中，确定收放机构在一次收放运动中的平均磨损增量可以包括：确定铰链结构在一次收放运动中的平均磨损增量，并作为收放机构在一次收放运动中的平均磨损增量。该铰链结构可以包括能够相对转动的两个部件，确定铰链结构在一次收放运动中的平均磨损增量可以包括：根据第一预设关系式确定铰链结构在一次收放运动中的平均磨损增量。该第一预设关系式可以为：

其中，h为平均磨损增量，t为起落架支柱进行一次收放运动所需要的时间，k为磨损系数，p为铰链结构中两个部件的接触点应力，v为铰链结构中两个部件的相对转动速度。该平均磨损增量为上述铰链结构的间隙的变化值。

在本公开其它实施方式中，可以采用archard模型对磨损增量进行计算，其表达形式如下：

式中，v为磨损体积，s为滑动距离，k为磨损系数，f为法向载荷，h为材料的布氏硬度。

步骤s101、确定起落架支柱的收放运动的次数。

步骤s102、根据平均磨损增量与收放运动的次数确定收放机构的磨损增量。

其中，该磨损增量可以等于平均磨损增量与收放运动的次数的积，即平均磨损增量乘以收放运动的次数的值。

在步骤s20中，根据收放机构的磨损增量对起落架进行可靠性分析。

其中，如图3所示，步骤s20可以包括：

步骤s200、确定起落架的失效模式。

该失效模式可以包括卡滞失效模式、定位失效模式以及精度失效模式中的一种或多种。

步骤s201、根据失效模式和收放机构的磨损增量对起落架进行可靠性分析。

以失效模式包括卡滞失效模式为例，根据失效模式和收放机构的磨损增量对起落架进行可靠性分析包括：根据收放机构的磨损增量确定g1(x)，g1(x)为收放机构能提供的最大推力减去起落架支柱进行收放运动所需的驱动力的值；若g1(x)小于零，即收放机构能提供的最大推力无法驱动起落架支柱进行收放运动，则判定起落架失效。

以失效模式包括定位失效模式为例，根据失效模式和收放机构的磨损增量对起落架进行可靠性分析包括：根据收放机构的磨损增量确定g2(x)，g2(x)为起落架支柱的收放运动能达到的最大角度减去起落架支柱的收放运动所需的最大角度的值；若g2(x)小于零，则判定起落架失效。其中，该起落架还可以包括上位锁。在g2(x)小于零时，判定上位锁无法实现锁住功能。

以失效模式包括精度失效模式为例，根据失效模式和收放机构的磨损增量对起落架进行可靠性分析包括：根据收放机构的磨损增量确定g3(x)，g3(x)为起落架支柱在最终放下时产生的角度差减去起落架支柱在最终放下时所允许的角度差；若g3(x)小于零，则判定起落架失效。其中，该起落架还可以包括下位锁。在g3(x)小于零时，判定下位锁无法实现锁住功能。

以失效模式包括卡滞失效模式、定位失效模式以及精度失效模式共三种失效模式为例，根据失效模式和收放机构的磨损增量对起落架进行可靠性分析包括：根据收放机构的磨损增量确定g1(x)，g2(x)以及g3(x)，若g1(x)，g2(x)以及g3(x)中至少存在一个小于零，则判定起落架失效。

上述g1(x)，g2(x)以及g3(x)中的x可以为m维随机变量，即x＝[x1，x2，…，xm]。其中，该x1可以为上述收放机构的铰链结构的磨损增量，该x2，…，xm可以为收放机构的其它部位的磨损增量，本公开在此不再详述。

此外，对工程实际问题进行可靠性分析时，通常需要借助仿真软件映射输入变量与输出响应之间的关系，但复杂机构的动力学分析复杂费时，特别是在对机构进行大量、反复的响应分析时，往往需要耗费大量的时间，效率低下。因此，通常使用代理模型来提高计算效率。目前比较常见的代理模型有响应面、神经网络和kriging模型等。其中，kriging模型以其预测能力强，局限性小而被广泛使用，它能用少量的样本得到给定精度要求的代理模型，减少了可靠性及灵敏度的计算量，提高了效率。

根据kriging理论，假设输出响应量g(x)与输入变量x之间的关系为：

g(x)＝f^t(x)β+z(x)；

其中，f(x)为回归多项式基函数向量，β为回归系数的向量，z(x)为零均值的高斯随机过程，协方差函数为：

其中，为高斯过程的方差。r(xi，xj；θ)为具有参数向量θ的相关函数，将其表示为：

给定一组样本点，则g(x)的无偏估计及预测误差定义如下：

原始的kriging代理模型法无法平衡精度与效率的矛盾，因为其无法保证用于构造kriging代理模型的样本点都是对预测精度具有显著贡献的点。为了提高代理模型的预测精度，本公开使用均方误差法来训练kriging代理模型，该方法挑选预测方差最大的点作为更新的训练样本点更新kriging代理模型，即

xnew＝argmaxs²(x)；

确定kriging模型构建的收敛条件为：

e＝|sm-s1|/s1≤5×10^-4；

式中sm＝maxs，s1为上一次未加点时的最大标准差。e值越小，kriging代理模型的预测精度越准。

本公开基于自适应kriging代理模型，对起落架收放机构进行可靠性和灵敏度分析，步骤包括：

步骤a10、抽取样本池，根据输入变量的联合概率密度函数产生样本池，该样本池由n＝10⁶个样本组成。

步骤a20、构建初始训练样本集，从样本池中抽取50组初始训练样本x0，调用adams仿真计算出响应值g0＝[fneed，anglemax，δ]，形成初始训练样本集。

步骤a30、构建模型，使用训练样本集(x0，g0)拟合出kriging模型。

步骤a40、选择更新样本点，根据公式xnew＝argmaxs²(x)，从样本池中选择更新的样本点xnew。

步骤a50、判别kriging模型自学习过程的收敛性，若e小于等于5×10^-4，停止学习过程，执行步骤a60；若e大于5×10^-4，将更新样本点xnew输入adams，计算g(xnew)，将{xnew，g(xnew)}加入训练样本池，更新kriging模型。

步骤a60、计算失效概率与灵敏度，基于最终建立的kriging模型，使用montecarlo法估计失效概率pf和灵敏度指标δi^p。

此外，尽管在附图中以特定顺序描述了本公开中方法的各个步骤，但是，这并非要求或者暗示必须按照该特定顺序来执行这些步骤，或是必须执行全部所示的步骤才能实现期望的结果。附加的或备选的，可以省略某些步骤，将多个步骤合并为一个步骤执行，以及/或者将一个步骤分解为多个步骤执行等。

本领域技术人员在考虑说明书及实践后，将容易想到本公开的其它实施方案。本申请旨在涵盖本公开的任何变型、用途或者适应性变化，这些变型、用途或者适应性变化遵循本公开的一般性原理并包括本技术领域中的公知常识或惯用技术手段。说明书和实施例仅被视为示例性的，本公开的真正范围和精神由所附的权利要求指出。