基于压缩感知技术的k-means算法

1.本发明涉及数据挖掘技术领域和数据分析技术领域，具体地说是一种基于压缩感知技术的k-means算法的改进方法。


背景技术：

2.数据挖掘指的是从大量的，无规则的，杂乱无章的数据中提取出或者挖掘出有用的，人们事先不知道的，但是它又是潜在的、有用的信息和知识的一个过程。数据挖掘的方法有很多，包括决策树分析、分类、聚类、关联规则、预言、估值、可视化等等。其中聚类是一种无监督学习的分类技术，聚类的目的是使同一类中的数据的相似度尽可能高，而且不同类的相异度也尽可能高，从而得到数据中潜在的分类信息。
3.聚类在各种科学领域具有悠久而丰富的历史。k-means是最流行和最简单的聚类算法之一，于1955年首次发布。尽管k-means是在50多年前提出的，并且自那时以来已经发布了数千种聚类算法，但k-means是仍然广泛使用。
4.lloyd-max算法是执行k-means聚类的传统经典方法。然而，随着训练数据集的增长，其计算成本变得过高。


技术实现要素：

5.本发明的目的在于提供了一种基于压缩感知技术的k-means聚类算法，有效避免了现有技术中面对大量数据集时算法计算复杂度高的缺陷。
6.本发明的技术解决方案为：一种基于压缩感知技术的k-means聚类算法的解决方案，具体步骤如下：
7.(1)从数据集x中得到频率数分布λ，并绘制出m个频率向量ω
j
；
8.步骤
①
，输入数据集x、参数n0≤n、m0、c和迭代次数t，估算出均值方差σ2；
9.步骤
②
，输入数据集的均值方差{∑
k
}
k＝1,2,
…
k
，权重α，频率数m，计算出频率数向量ω＝{ω1,ω2，
…
,ω
m
}；
10.(2)计算出数据集的草图；
11.步骤
①
，给定m个频率向量ω＝{ω1,ω2，
…
,ω
m
}；
12.步骤
②
，l个数据的数据集y的草图定义为
[0013][0014]
其中，频率ω1,ω2，
…
,ω
m
为概率分布p的特征函数的采样，定义
[0015][0016]
(3)使用ckm算法从草图中检索出质心集c。
[0017]
输入：草图频率向量ω,参数k,l，u；
[0018]
输出：质心集c,权重α
[0019]
初始化：
[0020]
for t
←
1to 2k do
[0021]
步骤1：发现新的质心
[0022][0023]
步骤2：扩展质心集
[0024]
c
←
c∪{c}
[0025]
步骤3：通过硬阈值实现稀疏性if t＞k
[0026]
if|c|＞k then
[0027][0028]
选择k个最大条目
[0029]
优化质心集
[0030]
步骤4：输出α
[0031][0032]
步骤5：降低梯度
[0033][0034]
步骤6：更新残差:
[0035][0036]
本发明设计了从草图中检索质心集的目标函数，所述目标函数为：
[0037]
其中α≥0，
[0038]
本发明与现有技术相比，其显著优点：该方法的聚类效果表现与k-means算法相似，因为草图的大小与原始数据集的大小无关，仅与质心个数k和数据维数n有关，则降低了算法的计算复杂度。对于大型数据集，通过实验表明改进算法比传统k-means算法更加优化。
附图说明
[0039]
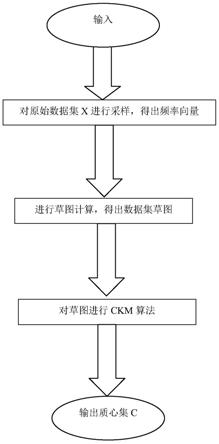
图1为本发明的方法流程图。
[0040]
图2为本发明的ckm算法的流程图。
[0041]
图3为采用本发明所提用方法和采用现有技术的目标函数sse性能对比示意图。
[0042]
图4为采用本发明所提用方法和采用现有技术的聚类效果rand index性能对比的示意图。
[0043]
图5为采用本发明所提用方法和采用现有技术的时间复杂度、空间复杂度和相关目标函数sse性能的对比示意图。
具体实施方式
[0044]
本发明一种基于压缩感知技术的k-means算法，主要利用原始数据集的草图来估计聚类中心，该方法提出了k-means的压缩版本(ckm)，它从草图中估计聚类中心，即从训练数据集的急剧压缩表示中估计聚类中心。该方法使用压缩学习正交匹配追踪替换算法(clompr)的变体从草图中检索质心，这是一种最初用于大规模高斯混合模型(gmm)估计的算法。它的复杂性读取o(nmk2)，因此一旦计算出草图，就完全消除了n的依赖性。还可以通过利用快速变换或在较低维度中嵌入作为预处理步骤，可以进一步降低这种复杂性。
[0045]
该方法主要包含以下步骤：(1)计算数据集频率数分布λ，并得到m个频率向量ω
j
；(2)计算数据集草图；(3)使用ckm算法进行聚类，得到质心集。相较于现有技术利用k-means聚类算法进行聚类，具有更优性能。
[0046]
下面结合具体实施例对本发明技术方案进一步说明。
[0047]
如图1所示，本发明一种基于压缩感知技术的k-means聚类方法，包括如下步骤：
[0048]
(1)从数据集x中得到频率数分布λ，并绘制出m个频率向量ω；
[0049]
首先，把数据集中每个对象表示成一个向量，即数据集x＝{x1,x2,
…
x
n
}，n为数据对象个数，其中每个数据对象表示为x
i
＝{x
i1
,x
i2
,
…
x
id
}，d为数据集中特征的数目。在算法运行时，需要把整个数据矩阵x加载到内存中。其次，输入参数n0≤n、m0、c和迭代次数t，估算出均值方差σ2。最后，输入数据集的均值方差{∑
k
}
k＝1,2,
…
k
，权重α，频率数m，计算出频率数向量ω＝{ω1,ω2，
…
,ω
m
}。
[0050]
(2)计算出数据集的草图；根据第一步的结果，利用公式计算出数据集的草图(2)计算出数据集的草图；根据第一步的结果，利用公式计算出数据集的草图
[0051]
其中，频率ω1,ω2，
…
,ω
m
为概率分布p的特征函数的采样，定义
[0052][0053]
(3)使用ckm算法从草图中检索出质心集c。
[0054]
输入：草图频率向量ω,参数k,l，u；
[0055]
初始化：
[0056]
for t
←
1to 2k do
[0057]
步骤1：发现新的质心
[0058][0059]
步骤2：扩展质心集
[0060]
c
←
c∪{c}
[0061]
步骤3：通过硬阈值实现稀疏性if t＞k
[0062]
if|c|＞k then
[0063][0064]
选择k个最大条目
[0065]
优化质心集
[0066]
步骤4：输出α
[0067][0068]
步骤5：降低梯度
[0069][0070]
步骤6：更新残差:
[0071][0072]
迭代步骤1、2、3、4、5和6，直到算法收敛，最后输出：质心集c,权重α
[0073]
本发明设计了从草图中检索质心集的目标函数，所述目标函数为：
[0074]
其中α≥0，
[0075]
为了客观评价本发明的效果，本实施例在一个真实数据上比较了本发明(ckm算法)与现有的k-means算法的聚类算法性能。对ckm的matlab实现与实现lloyd-max的matlab的k-means函数进行比较。本发明采用两种常用的聚类算法评价指标：目标函数sse和rand index来评价本发明和现有方法的性能。lloyd-max通常会随机初始化重复几次，并保留产生最低sse的质心集。在ckm算法中，实际上无法访问sse，因为在计算草图之后丢弃了数据。因此，当执行几次ckm重复时，选择最小化成本函数的质心集：
[0076][0077]
对mnist数据集进行谱聚类。实际上，为了测试本发明方法在大型数据集上的性
能，使用原始的7
·
104图像，使用infmnist的原始图像来创建图像。
[0078]
图1表示了在mnist数据集上，将超过100个sse实验的平均值和方差除以n，并进行1或10次重复。图2表示了调整后的rand指数用于比较mnist上1或10次迭代的聚类结果。图3表示了ckm算法的时间和记忆复杂度，相对于k-means的时间和记忆复杂度。
[0079]
正如预期的那样，k-means在多次执行时受益匪浅，而ckm在重复之间更加稳定。这使得ckm在实践中运行的重复次数少于实际的k均值(更多)。此外，对于大数据集(n＝1000000)，ckm的性能具有可忽略的方差，并且在1到10次重复之间具有可忽略的差异。因此，虽然草图的大小m保持固定为所有n，但是当应用于大数据集时，该方法实际上更有效。有趣的是，在所有情况下，ckm在分类中优于k均值。这可能意味着所提出的成本函数比sse更适应这一特定任务。
[0080]
计算草图的计算复杂性未在此图中概述，因为它可以在线和大规模并行化方式完成并且高度依赖于用户的可用硬件。正如预期的那样，给定草图ckm在大型数据集上的效率远高于k-means，即使对于大量频率也是如此。总体而言，在具有107个元素的数据集上，一次ckm运行速度比具有5个重复数据的k-means快150倍。
[0081]
以上以用实施例说明的方式对本发明作了描述，本领域的技术人员应当理解，本公开不限于以上描述的实施例，在不偏离本发明的范围的情况下，可以做出各种变化、改变和替换。