一种基于双梁模型的悬索桥精细化动力分析方法与流程

本发明属于结构动力学领域，特别涉及一种基于双梁模型的悬索桥精细化动力分析方法。

背景技术：

悬索桥由于其构造简单，受力明确，跨越能力强等被公认为是特大跨度桥梁的主要结构形式。大跨度悬索桥的动力特性分析通常采用有限元法进行，能否正确模拟结构刚度、质量和边界条件将直接影响分析结果的准确性，而动力特性又是结构抗风抗震分析的基础。由于悬索桥主缆不可更换，且其安全性对全桥的承重能力和安全性至关重要，因此有必要对其动力特性进行精细化建模分析。然而已有研究在对悬索桥进行建模分析时通常会对主缆进行简化，即采用杆单元进行建模，其垂度效应引起的几何非线性通常采用ernst等效弹性模量公式进行处理。这类处理方式在对主缆进行动力特性分析时会存在以下问题：(1)由于忽略了主缆的弯曲刚度，在对边缆或对于跨度较小的主缆进行分析时，其计算结果很可能误差较大；(2)难以计入由于主缆振动时由于弹性伸长引起的附加索力影响。

由于主缆在恒载作用下具有很大的初始张拉力，对后续结构形状提供强大的“重力刚度”，而加劲梁的挠度是从属于主缆的，随着跨度的增大，加劲梁自身的抗弯刚度对结构刚度的影响也逐渐减小。可见，有必要对悬索桥主缆进行精细化建模，发展一套悬索桥精细化动力分析理论，这就需要对已有悬索桥力学模型和分析理论进行改进。

技术实现要素：

本发明解决的技术问题是：本发明目的在于针对现有技术的不足，提出一种悬索桥精细化动力分析模型及求解方法，该模型将更加符合实际情况、能够更可靠地用于桥梁结构的结构设计、动力特性分析、以及振动控制等场合。

本发明的技术方案是：一种基于双梁模型的悬索桥精细化动力分析方法，包括以下步骤:

步骤一：基于双梁模型的悬索桥动力学建模，建立系统运动微分方程组，包括以下子步骤：

子步骤一：双梁模型由两个梁及若干离散弹簧组成，两个梁通过弹簧连接，分别用于模拟悬索桥主缆和主梁。各弹簧用于模拟悬索桥的吊杆，ki表示i个弹簧的刚度系数，大小等于第i个吊杆的轴向刚度；lsi表示第i个吊杆距离左端点的距离；模型中位于上方的具有垂度的梁代表悬索桥的主缆，下方的梁则用以模拟悬索桥的主梁，悬索桥的主跨跨径为l0；在振动过程中，主缆和主梁被吊杆分割的各个单元(分别称为索段和梁段)将遵循不同的运动构型，因此需要在各索段和梁段上分别建立局部坐标系；定义第i个索段和梁段分别为sci和sgi，二者的局部坐标系分别为(xci,yci)和(xgi,y)，系统的整体坐标系为(x,y)；

子步骤二：依据哈密顿原理，建立局部坐标系下悬索桥各索段和梁段的运动微分方程如下：

其中e1i1(e2i2)、m1(m2)、h1(h2)分别为主缆(主梁)的抗弯刚度、每延米质量、以及承受的水平张(压)力；u1i及u2i分别为主缆和主梁第i个单元的位移函数；()′代表对局部坐标系下的空间坐标xci或xgi求导，(·)表示对时间t求导；δ(·)为狄拉克函数；yi为主缆第i个索段的初始静构型；θi为第i个吊杆与主缆法向所夹锐角；

式中hi为主缆第i个索段振动时由于弹性伸长引起的附加索力，计算式如下：

其中a1和εi(t)表示主缆的横截面面积和索段的动应变，li为第i个索段的轴向长度，其值可由li＝lsi-lsi-1确定；表示i个索段的曲线长度；

步骤二：对(1)和(2)式应用分离变量法并求其通解，得到主缆和主梁的无量纲化后的振型函数和如下：

其中μi＝li/l0，ξ1i＝xci/x，ξ2i＝xgi/x，其中n＝1,2，1代表主缆而2代表主梁；

其中μsi＝lsi/l0；

(4)和(5)式中的系数为未知常数，它们取决于结构的边界条件，可在后续分析过程中通过代换先行消去，在求得了系统模态频率ω后予以确定。

步骤三：计算单元动刚度矩阵k^(j)，包括以下子步骤：

子步骤一：为了表述方便，将(4)式和(5)式进一步写为如下矩阵形式：

其中

其中

由(9)式求得b⁽ⁱ⁾后，根据结点位移u⁽ⁱ⁾与位移函数的关系可以将第i个索段和梁段的结点位移向量u⁽ⁱ⁾统一表示为：

u⁽ⁱ⁾＝c⁽ⁱ⁾·a⁽ⁱ⁾(10)

其中和分别表示第i个索段左端结点的位移和转角，和分别表示第i个索段右端结点的位移和转角；和分别表示第i个梁段左端结点的位移和转角，和分别表示第i个梁段右端结点的位移和转角；

cni＝cos(qnμi),sni＝sin(qnμi),n＝1,2。

再结合结点力平衡条件可得

其中

其中ν＝e2i2/e1i1。式(11)可进一步写为

f⁽ⁱ⁾＝k⁽ⁱ⁾·u⁽ⁱ⁾(12)

其中单元刚度矩阵k⁽ⁱ⁾可由下式确定

步骤四：对各单元刚度矩阵k⁽ⁱ⁾进行集组，得到整体坐标系下的总体动刚度矩阵k。

矩阵k是一关于系统模态频率ω的方阵，ω是频率方程|k(ω)|＝0的根。其中|·|为行列式符号。频率方程|k(ω)|＝0的求解可借助常规数值迭代算法来实现，如newton法或muller法等，进而可得系统的各阶模态频率ω；

步骤五：将求得的模态频率ω代入(4)和(5)式，再结合边界条件确定待定系数进而可求得系统的各阶模态振型和

本发明进一步的技术方案是：所述步骤四中的矩阵k是一个关于系统模态频率ω的方阵，其中ω即为频率方程|k(ω)|＝0的各个根；|·|为行列式符号；该方程的精确求解可采用netwon法、muller算法等常规数值迭代算法求解，进而可得系统的各阶模态频率ω。

发明效果

本发明的技术效果在于：

1.目前，对悬索桥动力特性的求解缺乏快速有效的分析方法，致使其动力分析多采用以有限元法为代表的数值解法，因此计算效率较低，不便于进行批量化参数分析。本发明提出的方法是一种频域解法，其求解过程全部是闭合形式的，因此相比于传统时域解法具有更高的计算效率和精度。

2.本发明方法过程简单，根据动力刚度法给出了悬索桥频率方程的闭合解，通过解此频率方程实现了系统模态频率和振型的求解。本发明建立了一套完整的、充分考虑悬索桥主缆、主梁、以及吊杆刚度影响的精细化动力学模型，同时给出了系统动力特性的一般化求解流程，以便于工程人员应用于悬索桥结构优化设计、健康监测、以及振动控制等。

3.附图说明

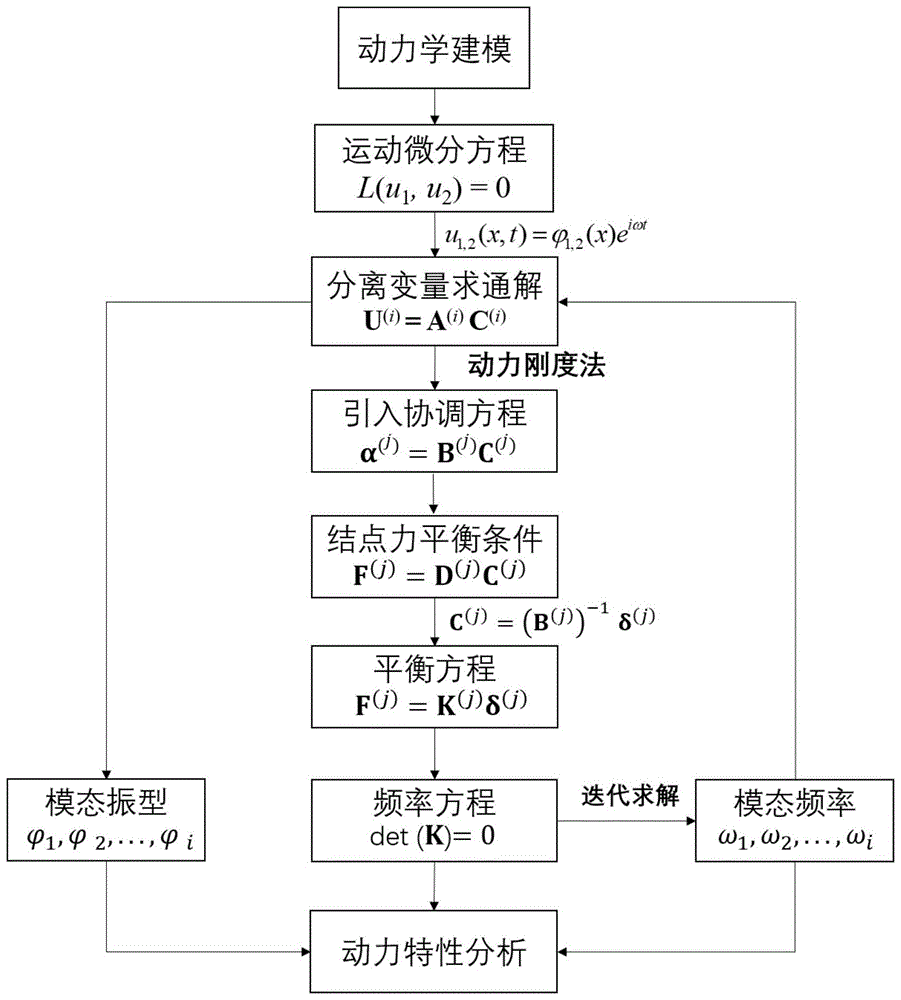
图1为计算流程图

图2为单跨悬索桥简化动力学模型图

具体实施方式

参见图1—图2，本发明所述的大跨度悬索桥精细化动力分析方法包括以下步骤：

1.依据本发明提出的双梁模型对悬索桥进行动力学建模(附图2)，依据哈密顿原理建立其运动微分方程组；

2.计算被吊杆划分的主缆各索段的附加索力hi，建立局部坐标系下各索段的运动微分方程，采用分离变量法将其变换至频域并求其振型函数

3.由hj计算主缆各索段的垂度矩阵b⁽ⁱ⁾，再结合结点位移连续条件及力平衡条件计算过度矩阵c⁽ⁱ⁾和d⁽ⁱ⁾，最后计算单元动刚度矩阵k⁽ⁱ⁾：

其中n＝1代表主缆，n＝2代表主梁。

4.对各单元动刚度矩阵进行集组，得到悬索桥的整体动刚度矩阵k；

5.依据wittrick-williams算法计算频率方程|k(ω)|＝0，该超越方程的根即系统的各阶模态频率；

6.将求得的模态频率ω代入通解结合边界条件求解待定系数进而得到对应模态振型。

下面对本发明技术方案进行详细说明，但本发明的保护范围不局限于所述实施例。如图1所示，本发明所述一种单跨悬索桥的快速精细分析方法，包括以下步骤：

1.建立如附图2所示的悬索桥动力学模型，依据哈密顿原理建立悬索桥运动微分方程如下：

其中e1i1(e2i2)、m1(m2)、h1(h2)分别为主缆(主梁)的抗弯刚度、每延米质量、以及承受的水平张(压)力；u1i及u2i分别为主缆和主梁第i个单元的位移函数；ki为第i个吊杆的刚度；()′代表对空间坐标x求导，(·)表示对时间t求导；lsi表示第i个吊杆所在横坐标位置；δ(·)为狄拉克函数；yi为主缆第i个索段的初始构型；θii为主缆法向与吊杆所夹锐角。

为主缆第i个索段振动时由于弹性伸长引起的附加索力。

2.主缆和主梁振型函数及的求解

将和代入(15)式和(16)式并进行无量纲化处理求其通解即可得到主缆和主梁各单元的振型函数如下：

其中li为第i个单元的长度(见附图2)，l0为悬索桥主跨跨径，

其中8个待定系数可由索单元和梁单元的边界条件予以确定，即待定系数应满足如下关系：

cni＝cos(qnμi),sni＝sin(qnμi),n＝1,2。

3.单元动刚度矩阵k⁽ⁱ⁾的求解

(4)和(5)式可进一步表示为如下矩阵形式：

其中

其中

求得b⁽ⁱ⁾后，根据结点位移u⁽ⁱ⁾与位移函数的关系可以将结点位移表示为：

u⁽ⁱ⁾＝c⁽ⁱ⁾·a⁽ⁱ⁾(24)

其中

cni＝cos(qnμi),sni＝sin(qnμi),n＝1,2。

再结合结点力平衡条件可得

其中

其中ν＝e2i2/e1i1。式(25)可进一步写为

f⁽ⁱ⁾＝k⁽ⁱ⁾·u⁽ⁱ⁾(26)

其中

4.整体动刚度矩阵k的求解

根据吊杆竖向刚度ki和单元动刚度矩阵k^(j)，即可按照与有限元法单元刚度矩阵集组过程相同的方法，通过叠加各单元对整体结构的刚度贡献得到整体刚度矩阵k，进而得到整体坐标系下的整体动刚度矩阵k。

上式是一个具有双吊杆的悬索桥的整体动刚度矩阵，其中，矩阵中各元素的上下标意义与单元刚度矩阵k^(j)中的元素一致。

5.频率方程的求解

得到整体刚度矩阵k后，求解特征方程det(k(ω))＝0即可求得系统的各阶模态频率ω。该方程通常为超越方程，可通过数值迭代算法求解，例如newton法和muller法等。

6.振型的求解

求得系统第i阶模态频率ωi后，可将其回代至(4)和(5)式可得和再将二者的表达式代入(20)式即可求得系数最终确定出主缆和主梁的模态振型和