一种系统级分析模型各部件动力贡献度分析方法及系统与流程

本发明涉及反应堆结构力学领域，具体涉及一种系统级分析模型各部件动力贡献度分析方法及系统。

背景技术：

反应堆主要系统(冷却剂系统、反应堆系统、净化系统、辅助系统等)的动力分析和载荷分配计算是反应堆和其附属系统结构设计中的重要环节，是对结构安全性评估的主要技术手段。系统级的动力分析与计算是开展反应堆系统载荷分配研究和安全分析的上游。系统级动力分析模型通常包括反应堆及一回路系统中的主要设备(如，反应堆压力容器、冷却剂主泵、蒸汽发生器、稳压器)、管道(如，主管道、辅助管道)和其他辅助系统(如，余热排出系统、净化系统等)等。系统级动力分析模型通常通过有限元方法建立，通过对各主要设备和部件的简化，抽象出能够描述系统主要动力特征的力学模型。其主要是用来计算系统在受到外界动态载荷作用下(如，地震、loca、冲击等)各主要设备与部件的位移与反作用力，为进一步细化分析各部件的承载强度和应力评估提供计算输入。

系统级动力分析主要通过频域内的模态分析、谱分析、谐响应分析及时域内的非线性瞬态分析的方式展开。由于系统级模型中通常包括大量的非线性因素，且模型规模较为庞大，因此通过全尺寸模拟系统级模型来获得单个部件或设备的动态响应贡献程度将会耗费大量机时和计算代价。如何通过一种快速的方法考察系统级模型在特定载荷条件下各部件的动力贡献程度，是分析部件动力特性的重要因素。

现阶段工程上主要通过模态分析的方法来考察整个系统的动态特性。尽管模态分析能够给出系统在一定频段内的共振频率与振型分布，但现有的分析方法与计算软件无法给出系统级模型中某个设备或部件的主导共振频率和主要参与质量。工程中常用的方法是通过观察特定模态下系统所有节点的振型位移，进而定性判断某阶共振频率下运动幅度较大的部件。由于模态分析中的振型函数通常针对系统模型的质量矩阵进行了归一化处理，因此这种定性的判断方法无法在物理坐标上给出真实的部件动力贡献度描述，仅能根据分析者的工程经验给出大致的判断，无法在设备的设计初期就给出快速的力学设计建议。

综上所述，发明人在实现本申请实施例中发明技术方案的过程中，发现现阶段的技术至少存在如下问题：

1.现有公开发表的文献与资料缺少针对系统级动力分析模型下对各部件动力贡献程度的定量研究。

2.工程中通过定性观察系统级模型的振型分布来确定部件动力贡献度的方式缺乏理论支承，且无法给出定量描述。

3.通过开展系统级模型非线性瞬态分析获取单个部件动力贡献度的方式计算代价较高，不利于系统设计初期的快速迭代。

技术实现要素：

本发明所要解决的技术问题是现有技术中缺少针对系统级动力分析模型下对各部件动力贡献程度分析技术，无法对各部件动力贡献程度给出定量描述，目的在于提供一种系统级分析模型各部件动力贡献度分析方法及系统，解决上述问题。

本发明通过下述技术方案实现：

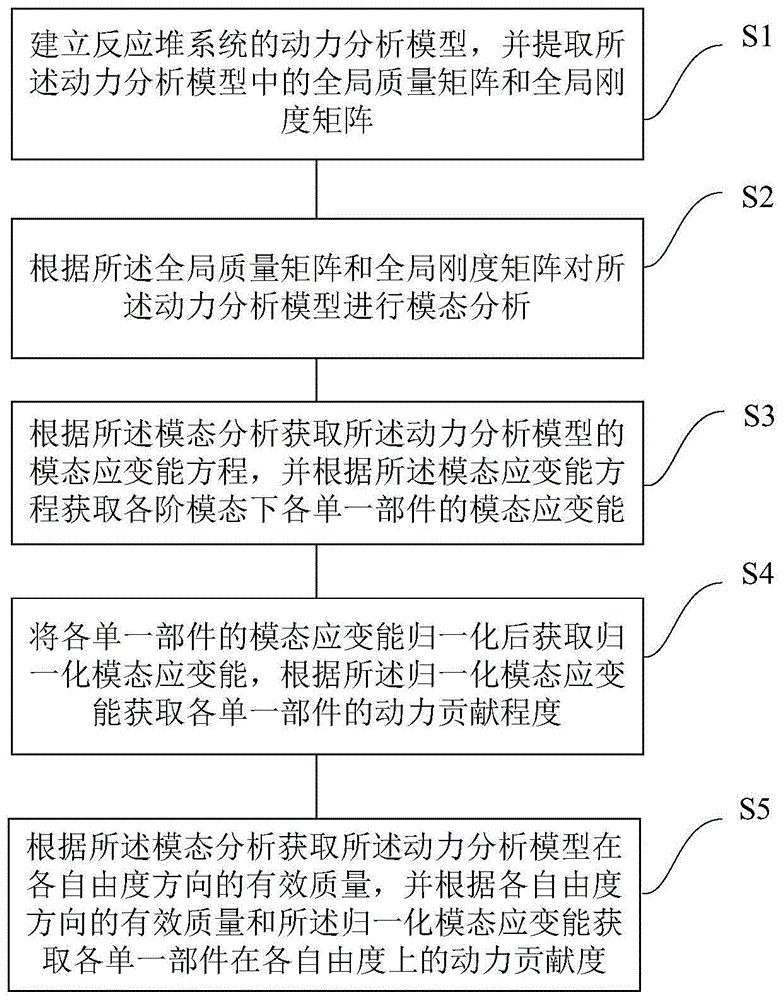
一种系统级分析模型各部件动力贡献度分析方法，包括：s1：建立反应堆系统的动力分析模型，并提取所述动力分析模型中的全局质量矩阵和全局刚度矩阵；s2：根据所述全局质量矩阵和全局刚度矩阵对所述动力分析模型进行模态分析；s3：根据所述模态分析获取所述动力分析模型的模态应变能方程，并根据所述模态应变能方程获取各阶模态下各单一部件的模态应变能；s4：将各单一部件的模态应变能归一化后获取归一化模态应变能，根据所述归一化模态应变能获取各单一部件的动力贡献程度。

本发明应用时，建立反应堆系统的动力分析模型可以采用有限元、离散元等离散模型的方式建立，动力分析模型中的关键部件包括有：燃料组件(fa)、堆芯吊篮(cb)、上部堆内构件(uvi)、堆芯围桶(cs)、控制棒驱动机构(crdm)、反应堆压力容器(rpv)、一体化堆顶结构(uvi)。在建立模型后可以从动力分析模型中提取出全局质量矩阵m和全局刚度矩阵k；根据m和k就可以对动力分析模型进行模态分析，模态分析可以得出动力分析模型各阶模态的固定频率和振型，各阶模态的固定频率和振型是后续分析的基础数据；通过模态分析可以获得动力分析模型的模态应变能方程，模态应变能方程是包含固定频率、振型、全局质量矩阵和全局刚度矩阵的方程，在这个方程的基础上，对全局刚度矩阵分解就可以获取各阶模态下各单一部件的模态应变能，对各单一部件的模态应变能归一化后就可以获取各单一部件的动力贡献程度。本发明提供的计算方法仅需要考察系统级模型的模态信息，并对全局质量和刚度矩阵进行分块操作即可，避免了直接开展非线性系统级模型瞬态分析的所需高昂计算代价和机时。该方法可在开展瞬态分析前的预处理阶段深入挖掘系统的动态特征和信息，在反应堆结构力学的标准分析流程中可得到推广。

进一步的，还包括以下步骤：

s5：根据所述模态分析获取所述动力分析模型在各自由度方向的有效质量，并根据各自由度方向的有效质量和所述归一化模态应变能获取各单一部件在各自由度上的动力贡献度。

本发明应用时，在各自由度方向的有效质量可以通过加入位移载荷向量的方式获取，本发明将有效质量和归一化模态应变能可以获取各单一部件在各自由度上的动力贡献度。

进一步的，根据下式获取所述动力分析模型在各自由度方向的有效质量：

式中为j阶模态下动力分析模型的有效质量；γj为模态参与因子；为第j阶模态的振型；m为所述动力分析模型的全局质量矩阵；d为位移载荷向量；

根据下式获取各单一部件在各自由度上的动力贡献度：

式中x为自由度方向；为p节点在第j阶模态x自由度方向下的动力贡献度；ωj为第j阶模态的固有频率；为p节点在第j阶模态的振型；kpq为动力分析模型全局刚度矩阵中的分块矩阵；为j阶模态下动力分析模型在x自由度方向的有效质量。

本发明应用时，d为位移载荷向量，这是在系统约束处某自由度方向施加单位位移时系统其他节点的位移向量，而x为自由度是表征的x代表可能出现的所有自由度，包括但不限于每个节点的三个平动方向和上转动方向的自由度；动力分析模型中的部件都是离散化的，各个部件在离散成多个单元时，单元自身会具有多个节点，通过节点可以表征部件的特征。在上述公式中，n为所考察不同部件和其不同自由度所对应节点集合的个数。p(p＝1,...,n)为所考察部件在系统级模型中所对应的节点集编号。

进一步的，步骤s5包括以下子步骤：

s51：对各自由度方向的有效质量进行无量纲化处理获取各阶模态下有效质量参与总质量的百分比；

s52：获取各单一部件在各自由度上的动力贡献度时，将有效质量参与总质量的百分比低于阈值的模态忽略。

本发明应用时，动力响应分析是一个运算量巨大的计算过程，尤其在加入了自由度方向以后，运算量会呈几何倍增长，所以为了提高运算效率，本发明还对各自由度方向的有效质量进行无量纲化处理获取各阶模态下有效质量参与总质量的百分比，并将，将有效质量参与总质量的百分比低于阈值的模态忽略，以此提高运算效率。

进一步的，步骤s2中，根据下式对所述动力分析模型进行模态分析：

式中ωj为第j阶模态的固有频率；为第j阶模态的振型；m为所述动力分析模型的全局质量矩阵；k为所述动力分析模型的全局刚度矩阵。

进一步的，步骤s3包括以下子步骤：对所述模态应变能方程中的全局刚度矩阵进行分块，并根据分块矩阵的乘法规则获取各阶模态下各单一部件的模态应变能。

本发明应用时，一个分块矩阵可以表征一个节点、一个单元或者一个部件的刚度，通过分块矩阵的方式，可以将所需要的数据从全局刚度矩阵中进行提取。

进一步的，所述模态应变能方程为：

式中ωj为第j阶模态的固有频率；为第j阶模态的振型；m为所述动力分析模型的全局质量矩阵；k为所述动力分析模型的全局刚度矩阵；

根据下式对所述模态应变能方程中的全局刚度矩阵进行分块：

式中k11至knn均为全局刚度矩阵中的分块矩阵；

根据下式获取各阶模态下各单一部件的模态应变能：

式中为p节点在第j阶模态下的模态应变能；kpq为动力分析模型全局刚度矩阵中的分块矩阵。

进一步的，步骤s4中将各单一部件的模态应变能归一化后获取归一化模态应变能采用下式获取：

式中为p节点在第j阶模态下的归一化模态应变能；kpq为动力分析模型全局刚度矩阵中的分块矩阵。

一种系统级分析模型各部件动力贡献度分析系统，包括：

建模单元：用于建立反应堆系统的动力分析模型；

提取单元：用于提取所述动力分析模型中的全局质量矩阵和全局刚度矩阵；

分析单元：用于根据所述全局质量矩阵和全局刚度矩阵对所述动力分析模型进行模态分析；

处理单元：用于根据所述模态分析获取所述动力分析模型的模态应变能方程，并根据所述模态应变能方程获取各阶模态下各单一部件的模态应变能；

归一化单元：用于将各单一部件的模态应变能归一化后获取归一化模态应变能，根据所述归一化模态应变能获取各单一部件的动力贡献程度；

自由度分析单元：用于根据所述模态分析获取所述动力分析模型在各自由度方向的有效质量，并根据各自由度方向的有效质量和所述归一化模态应变能获取各单一部件在各自由度上的动力贡献度。

进一步的，所述处理单元对所述模态应变能方程中的全局刚度矩阵进行分块，并根据分块矩阵的乘法规则获取各阶模态下各单一部件的模态应变能。

本发明与现有技术相比，具有如下的优点和有益效果：

本发明一种系统级分析模型各部件动力贡献度分析方法及系统，提供了一种考察系统级动力分析模型中各部件动力贡献度的计算方法，解决了当前工程中无法在特定自由度上对部件动力贡献度进行定量计算的现状。该方法适用于反应堆冷却剂系统的动态分析和计算。该方法能够在考虑系统中不同设备或部件存在耦合的情况下分析各部件的动态响应贡献度，其适用的动力分析载荷工况包括反应堆结构力学分析中常见的地震、loca、冲击等。本发明提供的计算方法仅需要考察系统级模型的模态信息，并对全局质量和刚度矩阵进行分块操作即可，避免了直接开展非线性系统级模型瞬态分析的所需高昂计算代价和机时。该方法可在开展瞬态分析前的预处理阶段深入挖掘系统的动态特征和信息，在反应堆结构力学的标准分析流程中可得到推广。

附图说明

此处所说明的附图用来提供对本发明实施例的进一步理解，构成本申请的一部分，并不构成对本发明实施例的限定。在附图中：

图1为本发明方法步骤示意图；

图2为本发明实施例方法步骤示意图；

图3为本发明实施例反应堆系统动力分析计算模型示意图；

图4为本发明实施例反应堆系统结构示意图；

图5为本发明实施例反应堆系统所受地震载荷响应谱；

图6为本发明实施例反应堆系统不同方向下模态有效质量的分布；

图7为本发明实施例反应堆系统不同部件动力贡献度分布；

图8为本发明实施例反应堆系统单个部件不同自由度动力贡献度分布。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚明白，下面结合实施例和附图，对本发明作进一步的详细说明，本发明的示意性实施方式及其说明仅用于解释本发明，并不作为对本发明的限定。

实施例1

如图1所示，本发明一种系统级分析模型各部件动力贡献度分析方法，包括：s1：建立反应堆系统的动力分析模型，并提取所述动力分析模型中的全局质量矩阵和全局刚度矩阵；s2：根据所述全局质量矩阵和全局刚度矩阵对所述动力分析模型进行模态分析；s3：根据所述模态分析获取所述动力分析模型的模态应变能方程，并根据所述模态应变能方程获取各阶模态下各单一部件的模态应变能；s4：将各单一部件的模态应变能归一化后获取归一化模态应变能，根据所述归一化模态应变能获取各单一部件的动力贡献程度。

本实施例实施时，建立反应堆系统的动力分析模型可以采用有限元、离散元等离散模型的方式建立，动力分析模型中的关键部件包括有：燃料组件(fa)、堆芯吊篮(cb)、上部堆内构件(uvi)、堆芯围桶(cs)、控制棒驱动机构(crdm)、反应堆压力容器(rpv)、一体化堆顶结构(uvi)。在建立模型后可以从动力分析模型中提取出全局质量矩阵m和全局刚度矩阵k；根据m和k就可以对动力分析模型进行模态分析，模态分析可以得出动力分析模型各阶模态的固定频率和振型，各阶模态的固定频率和振型是后续分析的基础数据；通过模态分析可以获得动力分析模型的模态应变能方程，模态应变能方程是包含固定频率、振型、全局质量矩阵和全局刚度矩阵的方程，在这个方程的基础上，对全局刚度矩阵分解就可以获取各阶模态下各单一部件的模态应变能，对各单一部件的模态应变能归一化后就可以获取各单一部件的动力贡献程度。本发明提供的计算方法仅需要考察系统级模型的模态信息，并对全局质量和刚度矩阵进行分块操作即可，避免了直接开展非线性系统级模型瞬态分析的所需高昂计算代价和机时。该方法可在开展瞬态分析前的预处理阶段深入挖掘系统的动态特征和信息，在反应堆结构力学的标准分析流程中可得到推广。

为了进一步的说明本实施例的工作过程，还包括以下步骤：

s5：根据所述模态分析获取所述动力分析模型在各自由度方向的有效质量，并根据各自由度方向的有效质量和所述归一化模态应变能获取各单一部件在各自由度上的动力贡献度。

本实施例实施时，在各自由度方向的有效质量可以通过加入位移载荷向量的方式获取，本发明将有效质量和归一化模态应变能可以获取各单一部件在各自由度上的动力贡献度。

为了进一步的说明本实施例的工作过程，根据下式获取所述动力分析模型在各自由度方向的有效质量：

式中为j阶模态下动力分析模型的有效质量；γj为模态参与因子；为第j阶模态的振型；m为所述动力分析模型的全局质量矩阵；d为位移载荷向量；

根据下式获取各单一部件在各自由度上的动力贡献度：

式中x为自由度；为p节点在第j阶模态x自由度下的动力贡献度；ωj为第j阶模态的固有频率；为p节点在第j阶模态的振型；kpq为动力分析模型全局刚度矩阵中的分块矩阵；为j阶模态下动力分析模型在x自由度的有效质量。

本实施例实施时，d为位移载荷向量，这是在系统约束处某自由度方向施加单位位移时系统其他节点的位移向量，而x为自由度是表征的x代表可能出现的所有自由度，包括但不限于每个节点的三个平动方向和上转动方向的自由度；动力分析模型中的部件都是离散化的，各个部件在离散成多个单元时，单元自身会具有多个节点，通过节点可以表征部件的特征。在上述公式中，n为所考察不同部件和其不同自由度所对应节点集合的个数。p(p＝1,...,n)为所考察部件在系统级模型中所对应的节点集编号。

为了进一步的说明本实施例的工作过程，步骤s5包括以下子步骤：

s51：对各自由度方向的有效质量进行无量纲化处理获取各阶模态下有效质量参与总质量的百分比；

s52：获取各单一部件在各自由度上的动力贡献度时，将有效质量参与总质量的百分比低于阈值的模态忽略。

本实施例实施时，动力响应分析是一个运算量巨大的计算过程，尤其在加入了自由度方向以后，运算量会呈几何倍增长，所以为了提高运算效率，本发明还对各自由度方向的有效质量进行无量纲化处理获取各阶模态下有效质量参与总质量的百分比，并将，将有效质量参与总质量的百分比低于阈值的模态忽略，以此提高运算效率。

为了进一步的说明本实施例的工作过程，步骤s2中，根据下式对所述动力分析模型进行模态分析：

式中ωj为第j阶模态的固有频率；为第j阶模态的振型；m为所述动力分析模型的全局质量矩阵；k为所述动力分析模型的全局刚度矩阵。

为了进一步的说明本实施例的工作过程，步骤s3包括以下子步骤：对所述模态应变能方程中的全局刚度矩阵进行分块，并根据分块矩阵的乘法规则获取各阶模态下各单一部件的模态应变能。

本实施例实施时，一个分块矩阵可以表征一个节点、一个单元或者一个部件的刚度，通过分块矩阵的方式，可以将所需要的数据从全局刚度矩阵中进行提取。

为了进一步的说明本实施例的工作过程，所述模态应变能方程为：

式中ωj为第j阶模态的固有频率；为第j阶模态的振型；m为所述动力分析模型的全局质量矩阵；k为所述动力分析模型的全局刚度矩阵；

根据下式对所述模态应变能方程中的全局刚度矩阵进行分块：

式中k11至knn均为全局刚度矩阵中的分块矩阵；

根据下式获取各阶模态下各单一部件的模态应变能：

式中为p节点在第j阶模态下的模态应变能；kpq为动力分析模型全局刚度矩阵中的分块矩阵。

进一步的，步骤s4中将各单一部件的模态应变能归一化后获取归一化模态应变能采用下式获取：

式中为p节点在第j阶模态下的归一化模态应变能；kpq为动力分析模型全局刚度矩阵中的分块矩阵。

实施例2

本实施例一种系统级分析模型各部件动力贡献度分析系统，包括：

建模单元：用于建立反应堆系统的动力分析模型；

提取单元：用于提取所述动力分析模型中的全局质量矩阵和全局刚度矩阵；

分析单元：用于根据所述全局质量矩阵和全局刚度矩阵对所述动力分析模型进行模态分析；

处理单元：用于根据所述模态分析获取所述动力分析模型的模态应变能方程，并根据所述模态应变能方程获取各阶模态下各单一部件的模态应变能；

归一化单元：用于将各单一部件的模态应变能归一化后获取归一化模态应变能，根据所述归一化模态应变能获取各单一部件的动力贡献程度；

自由度分析单元：用于根据所述模态分析获取所述动力分析模型在各自由度方向的有效质量，并根据各自由度方向的有效质量和所述归一化模态应变能获取各单一部件在各自由度上的动力贡献度。

为了进一步的说明本实施例的工作过程，所述处理单元对所述模态应变能方程中的全局刚度矩阵进行分块，并根据分块矩阵的乘法规则获取各阶模态下各单一部件的模态应变能。

实施例3

本实施例在实施例1和实施例2的基础上，

本申请实施例提供了一种反应堆系统中几种关键部件在沿反应堆压力容器轴线方向上动态贡献度的分析方法，所述方法包括：

1、利用有限元计算程序对反应堆系统进行动力分析建模。模型包括的关键部件包括：燃料组件(fa)、堆芯吊篮(cb)、上部堆内构件(uvi)、堆芯围桶(cs)、控制棒驱动机构(crdm)、反应堆压力容器(rpv)、一体化堆顶结构(uvi)。

2、提取系统级动力分析模型中的全局质量和刚度矩阵，记为m和k，将系统级模型的质量和刚度矩阵以稀疏矩阵的存储形式记录在文本文件中。

3、根据系统级模型的质量和刚度矩阵开展模态分析，如公式(1)所示。通过振型函数计算系统级模型在各自由度方向的有效质量，如公式(2)所示，并对有效质量进行无量纲化处理，如公式(3)所示。

4、根据模态分析，可得知系统级模型的模态应变能存在如公式(4)所示的关系。通过对全局刚度矩阵k进行分块操作，根据分块矩阵的乘法规则，可得某阶模态下单个部件的模态应变能，如公式(6)所示。矩阵的分块根据所考察部件及其自由度所属的有限元模型节点集合开展。矩阵分块操作的关键技术如公式(5)所示。

5、利用振型函数的正交性及归一化属性，可将公式(6)所示的部件模态应变能进行归一化处理，以便考察部件的动力贡献程度，如公式(7)所示。

6、进一步地，当考虑部件在不同自由度方向上模态重要程度的权重时，可结合模态有效质量和归一化的模态应变能进行考察，如公式(8)所示。

量化考察系统级模型中某个部件在特定自由度下的动力贡献度时，以直方图的形式输出公式(7)和(8)在不同模态下的量化分布。

其中：

上述各公式中，公式(1)中m和k分别为系统级动力分析有限元模型的全局质量矩阵和刚度矩阵，ωj和为第j阶模态的固有频率和振型；公式(2)中向量d为在系统约束处某自由度方向施加单位位移时系统其他节点的位移向量，γj为模态参与因子，meff为模态有效质量；公式(3)中mtot为系统级模型的总质量；公式(5)中n为所考察不同部件和其不同自由度所对应节点集合的个数。

第j阶模态有效质量参与总质量百分比

r＝d约束后的向量，位移载荷向量

进一步地，当公式(3)中的r值低于一定的小量门限值时，可认为其对应自由度方向的模态对系统的整体响应不占主要地位，因此在考察部件动力贡献度时可忽略各方向质量比均比较小的模态。

进一步地，自由度方向包括有限元模型中每个节点的三个平动方向x、y、z以及三个转动方向rotx、roty、rotz。

进一步地，公式(6)和(7)中p(p＝1,...,n)为所考察部件在系统级模型中所对应的节点集编号。

进一步地，公式(8)中变量wrmse的下标x表征计权x自由度方向模态有效质量时的部件动态贡献指标，其他自由度方向的计算同公式(8)。

利用本发明提供的计算方法，能够定量研究和考察系统级动力分析模型中各设备或部件在特定自由度下的动力贡献程度。本发明所提供的方法无需针对系统级动力分析模型开展非线性瞬态分析，仅需要模态信息即可掌握部件的动力特性。应用本发明提供的方法，在设备或部件设计初期就可充分掌握其在存在系统耦合作用下的动态贡献程度，为设备和部件的初步力学设计和后续结构优化提供定量参考依据。本发明中所有过程由计算机程序实现，计算结果可靠，分析过程可集成在反应堆结构力学标准分析流程当中。

实施例4

本实施例在实施例1～3的基础上，针对一种压水堆反应堆系统在地震载荷下的动力响应分析，对反应堆系统不同关键部件在沿压力容器轴线方向上的动力贡献度进行了分析计算。反应堆系统关键部件包括：燃料组件(fa)、堆芯吊篮(cb)、上部堆内构件(uvi)、堆芯围桶(cs)、控制棒驱动机构(crdm)、反应堆压力容器(rpv)、一体化堆顶结构(uvi)等。反应堆系统的结构示意图和动力分析有限元模型的抽象表征见图3和图4。反应堆系统地震分析的动态载荷输入以三个水平方向的地震响应谱形式给出，见图5，响应谱的作为位置为反应堆进口管嘴交界位置处。

如图2所述，包括以下步骤：

s10，通过有限分析软件或程序建立系统级动力分析有限元模型，提取模型的全局质量矩阵m和刚度矩阵k，并以稀疏矩阵的存储方式将全局质量和刚度矩阵保存在文本文件中。

在步骤s10后，本申请实施例的方法便进入步骤s20，即：对系统级模型进行模态分析，模态分析的基本技术如公式(1)所示，同时计算不同自由度方向下各阶模态的有效质量，如公式(2)所示。本实施例中反应堆系统不同方向模态有效质量的分布见图6。

在步骤s20后，本申请实施例的方法便进入步骤s30，即：根据各自由度方向无量纲有效质量在不同模态下的分布，如公式(3)所示，选择系统级模型的主导模态进行部件动力贡献度考察。本实施例中，主导模态对应着图5中有效质量位于较高水平的模态。

在步骤s30后，本申请实施例的方法便进入步骤s40，即：根据不同设备或部件在系统级有限元模型中的节点分布，对全局刚度矩阵k以及各阶阵型进行分块操作，如公式(5)所示。

在步骤s40后，本申请实施例的方法便进入步骤s50，即：根据公式(6)和(7)，计算单个部件在系统级模型中的模态应变能和其归一化指标，反应堆系统不同部件在主导模态下归一化后的模态应变能分布见图7。

在步骤s50后，本申请实施例的方法便进入步骤s60，即：根据公式(8)，以各自由度方向无量纲模态有效质量为权重，计算各部件计权模态应变能在主导模态下的分布情况。本实施例以燃料组件(fa)为例，在图8中给出了考虑沿反应堆压力容器轴线方向模态有效质量计权的部件各自由度方向动态贡献度的分布。

在步骤s60后，本申请实施例的方法便进入步骤s70，即：将各部件动力贡献度在主导模态下的分布以直方图或柱状图形式予以展示。

在步骤s70后，本申请实施例的方法便进入步骤s80，即：输出部件动力贡献度分析结果。

其中，在图8所示的各自由度动态贡献中，ux、uy、uz表示各考察节点各向平动位移；rot表示各向转动方向位移的集合。

其中，在实际应用中，商用有限元软件包括：ansys、abaqus等，数值计算软件和编程语言包括：matlab、fortran、c/c++、python等。

以上所述的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施方式而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。