一种输电线路锚杆基础的设计方法与流程

本发明属于基础工程施工
技术领域：
，具体涉及一种输电线路锚杆基础的设计方法。
背景技术：
：输电铁塔基础作为输电线路的重要组成部分，其工程造价、施工工期和人力消耗在整个线路工程中占很大比重。随着建设项目环境保护要求地日益提高，电力工程对更加经济环保的基础型式的需求越来越强烈，而锚杆基础正是满足这一要求的新型基础。在输电线路锚杆基础施工中，确定锚杆入土深度时，需要考虑锚固界面粘结应力的分布和发展对锚杆基础上拔承载力的影响。现阶段工程设计中均采用锚固界面粘结应力均匀分布假设来计算锚杆上拔承载力，通过锚杆上拔承载力要求来确定锚杆埋入深度。但诸多锚杆基础真型试验已经表明，一般岩土体条件下，锚固界面上的粘结应力往往呈现先增大后减小的分布；同时实际岩土体离散性较大，工程应用时对粘结强度的取值往往偏于保守，既不经济也不合理。同时，在锚杆基础以往的工程应用及相关研究中，对下压荷载作用下锚杆基础的承载性状未有涉及，因此实际工程设计时往往忽略锚杆杆体的承压贡献，偏保守地认为群锚基础的下压荷载全部由承台下方的岩土体承担，因而承台尺寸由承台下岩土体的地基承载力特征值控制，造成工程投资的浪费。技术实现要素：本发明的目的就是为了解决上述
背景技术：
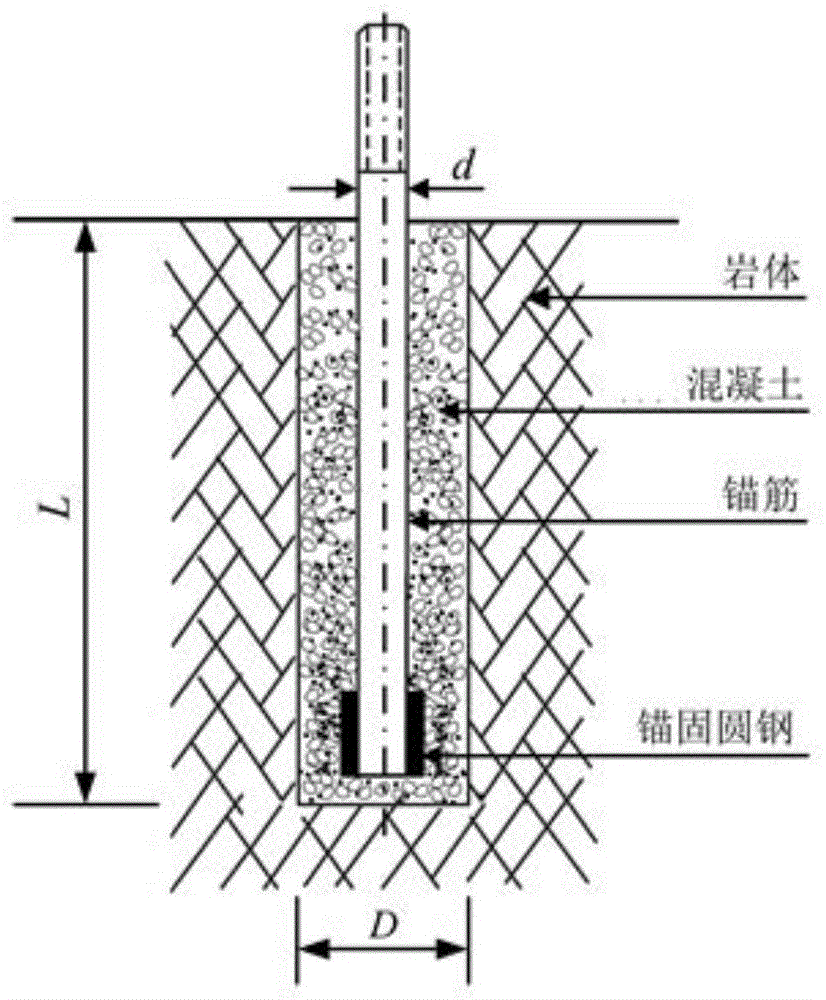
存在的不足，提供一种安全性和经济性高的输电线路锚杆基础的设计方法。本发明采用的技术方案是：一种输电线路锚杆基础的设计方法，包括设计锚杆埋深和锚杆根数，步骤为：s1：设定当次运算的锚杆根数及锚杆埋深；s2：基于基础上拔荷载、锚杆根数、群锚杆效应系数、地基水平力影响系数计算单锚杆极限上拔承载力目标值pu1；s3：以锚固界面粘结应力分布分段函数描述锚固界面粘结应力的实际分布，基于锚杆埋深、通过对锚固界面粘结应力分段函数积分得到单锚杆极限上拔承载力实际值pu；s4：比较单锚杆极限上拔承载力目标值pu1和单锚杆极限上拔承载力实际值pu，当单锚杆极限上拔承载力实际值pu大于等于单锚杆极限上拔承载力目标值pu1时，停止运算；当单锚杆极限上拔承载力实际值pu小于单锚杆极限上拔承载力目标值pu1时，则将当次运算的锚杆埋深增大一设定值作为下次运算的锚杆埋深或将当次运算的锚杆根数增大一设定数值作为下次运算的锚杆根数，重复步骤s1-s4，直到单锚杆极限上拔承载力实际值pu大于等于单锚杆极限上拔承载力目标值pu1时，停止运算；则停止运算时的锚杆埋深和锚杆根数为最终锚杆埋深和锚杆根数。进一步地，所述步骤s4中，当单锚杆极限上拔承载力实际值pu小于单锚杆极限上拔承载力目标值pu1时，将当次运算的锚杆埋深增大一设定值，并判断增大后的锚杆埋深是否大于埋深阈值：若增大后的锚杆埋深小于等于埋深阈值，则将增大后的锚杆埋深作为下次运算的锚杆埋深、将当次运算的锚杆根数作为下次运算的锚杆根数；若增大后的锚杆埋深大于埋深阈值，则将当次运算的锚杆埋深作为下次运算的锚杆埋深、将当次运算的锚杆根数增大一设定数值作为下次运算的锚杆根数。进一步地，通过以下公式计算单锚杆极限上拔承载力目标值pu1pu1＝tu/nηγe其中，pu1为单锚杆极限上拔承载力目标值；tu为基础上拔荷载，为标定值；n为锚杆根数；η为群锚杆效应系数；γe为地基水平力影响系数。进一步地，所述锚固界面粘结应力分布分段函数为：其中，τb(x)为锚杆上埋深x处的锚固界面粘结应力；x1为锚固界面粘结应力峰值位置对应的锚杆埋深；x0为锚固界面破坏段终点位置对应的锚杆埋深；τp为锚固界面峰值粘结应力；α为中间计算参数，d为锚筋直径。进一步地，通过以下公式计算单锚杆极限上拔承载力实际值pu其中，pu为单锚杆极限上拔承载力实际值，τp为锚固界面峰值粘结应力，d为锚筋直径，l为锚杆埋深，α为中间计算参数，x1为锚固界面粘结应力峰值位置对应的锚杆埋深。更进一步地，所述中间计算参数α通过以下公式确定：其中，d为锚筋直径；d为锚杆直径；d0为影响范围直径；eb为锚筋弹性模量；gr为岩体剪切模量；gg为注浆体剪切模量。进一步地，还包括设计群锚杆基础的承台面积：基于最终锚杆根数、群锚基础的下压荷载、承台下锚杆分担的下压荷载、岩土体的弹性模量和锚杆锚固体的弹性模量计算承台面积。更进一步地，通过以下公式计算承台面积其中：ac为承台面积；n为群锚基础的下压荷载；nm为承台下锚杆分担的下压荷载；f为承台下岩土体单位面积的承载力；am为锚杆的净截面面积，由锚杆根数与单锚杆的横截面积相乘得到；ec为岩土体的弹性模量；em为锚杆锚固体的弹性模量。本发明的有益效果是：本发明设计锚杆基础时，锚杆、承台参数确定基于锚固界面渐进破坏的全过程分析，考虑粘结应力沿锚杆-岩土界面全长分布，通过分段函数描述锚固界面粘结应力的实际分布，通过积分得到锚固界面的粘结承载力，最终在考虑群锚效应系数和水平力影响系数的基础上对群锚基础的上拔承载力进行全面验算，得出最合适的锚杆埋入深度及锚杆根数；同时也考虑了承台下锚固体对下压荷载的分担作用，按承台底岩土体的实际受力对承台尺寸进行复核调整，有利于减小承台尺寸，节省基础混凝土方量和减少弃土量。本发明的锚杆施工考虑的上拔承载力、下压承载力与锚杆基础的实际受力情况更加符合，有利于提高锚杆基础设计的安全可靠性，同时也具有较高的社会效益和经济效益。附图说明图1为本发明单锚基础的结构示意图。图2为本发明承台式锚杆基础的结构示意图。图3为本发明锚固界面粘结应力分布图。图4为本发明锚固界面粘结应力分布函数图。图5为本发明的设计流程图。具体实施方式下面结合附图对本发明的具体实施方式作进一步说明。在此需要说明的是，对于这些实施方式的说明用于帮助理解本发明，但并不构成对本发明的限定。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以互相结合。如图1、图2所示，锚杆埋深、锚杆根数及群锚基础承台面积是输电线路锚杆基础的重要设计参数，直接决定着输电线路的安全性能，而锚杆埋深、锚杆根数的取值直接决定了单锚杆极限上拔承载力，只有当单锚杆极限上拔承载力满足要求时，输电线路才能得到安全保障。本发明锚杆埋入深度及锚杆根数考虑了输电线路锚杆基础上拔的计算。本发明中，锚固界面粘结应力的分布发展过程简述如下：当上拔荷载较小时，锚固段前部锚固界面处于弹性阶段，锚固体与岩土体间未发生相对滑移，此时锚固体与岩土体变形协调一致，锚杆与地表交界点处的粘结应力值最大，且从最顶端开始向下呈负指数衰减，如附图3曲线a所示。随着上拔荷载的增大，最上部的粘结界面首先出现相对滑移并逐步向内发展，此时锚固段前段将出现部分破坏解耦段，破坏部分锚固界面上的粘结应力为0，接着界面粘结应力呈现线性增加至峰值然后再呈负指数衰减，如附图3曲线b所示。随着上拔荷载地进一步增大，锚杆及其上部结构将因为变形过大而不适于继续承载，此时的上拔荷载值即为锚杆的极限上拔承载力。基于上述发展过程，本发明提出采用包含破坏解耦段、上升段和衰减下降段三部分的锚固界面粘结应力分段函数来描述上拔荷载作用下锚固界面粘结应力的分布，函数图形如说明书附图4，具体如下式所示：中间计算参数α通过以下公式确定：其中：τb(x)为锚杆上埋深x处的锚固界面粘结应力；τp-锚固界面峰值粘接应力(mpa)；x1-锚杆粘接应力峰值位置对应的锚杆埋深；x0-锚固界面破坏段终点位置对应的锚杆埋深；d-锚筋直径(mm)；d-锚杆直径(mm)；d0-影响范围直径(mm)；eb-钢筋弹性模量(mpa)；gr-岩体剪切模量(mpa)；gg-注浆体剪切模量(mpa)。同时本发明做如下简化假设：1)锚固界面破坏段终点位置对应的锚杆埋深即x0取为0；2)锚杆粘接应力峰值位置对应的锚杆埋深x1按如下取值：未分化、微风化岩石25d，中风化岩石35d，强风化岩石及老黏土45d，d为锚筋直径；3)锚固界面峰值粘接应力取岩土体无侧限抗压强度的10％；4)锚杆影响范围直径取钻孔直径的10倍。在上述简化的基础上，本发明根据静力平衡条件，通过对上述锚固界面粘结应力分段函数进行积分可得到单锚杆极限上拔承载力实际值为：当单锚杆极限上拔承载力实际值满足施工要求时，就能确定锚杆埋深及锚杆根数。另一方面，单锚杆极限上拔承载力目标值pu1采用基础上拔荷载tu、群锚杆效应系数、地基水平力影响系数来共同表征，可表示为：pu1＝tu/nηγe其中，tu为基础上拔荷载，为标定值；η—群锚杆效应系数，本发明推荐当锚杆间距3d～4d时，取0.75～0.90；当锚杆间距为4d～8d时，取0.90～0.98；γe—地基水平力影响系数，本发明推荐老黏土取0.85，岩石地基取0.9，岩土体条件越好时取大值；n—锚杆根数。根据基础上拔荷载，结合前述单锚杆极限上拔承载力实际值及目标值的计算方法，通过验算得到满足单锚杆极限上拔承载力要求的锚杆根数及锚杆埋深，如图5所示，验算步骤如下：s1：已知基础上拔荷载t，令tu＝t，设定初始锚杆根数n(n一般取4、6、9、12中任意值)，则所需的单锚杆极限上拔承载力目标值为：pu1＝tu/nηγe＝t/nηγes2：设定初始锚杆埋深l(l一般取2-8m中任意值)，根据上述单锚杆上拔承载力实际值计算公式得到单锚杆极限上拔承载力实际值pu。s3：比较pu和pu1，当pu≥pu1时，所设定的锚杆根数n及锚杆埋深l满足要求；当pu＜pu1，重新调整锚杆根数n或锚杆埋深l，返回s1和s2，重新计算直到满足pu≥pu1，则最终确定锚杆埋深和锚杆根数。步骤s3中重新调整锚杆根数n或锚杆埋深l的过程如下：当pu＜pu1时，将当次运算的锚杆埋深增大一设定值δl，并判断增大后的锚杆埋深是否大于埋深阈值，设定值δl根据实际需要确定，如其大小可以为2～8m中任意值，埋深阈值为当前岩体地质及施工条件能到达的最大埋深；若增大后的锚杆埋深小于等于埋深阈值，则将增大后的锚杆埋深作为下次运算的锚杆埋深、将当次运算的锚杆根数作为下次运算的锚杆根数；若增大后的锚杆埋深大于埋深阈值，则将当次运算的锚杆埋深作为下次运算的锚杆埋深、将当次运算的锚杆根数增大一设定数值δn作为下次运算的锚杆根数，设定数值δn根据实际需要确定，如其大小可以为4、6、9、12中任意值。本发明在群锚杆的基础上设计承台时，考虑群锚基础在下压荷载作用下，承台底岩体及锚固体产生压缩变形，本发明即以承台截面变形协调条件为基础，按刚度分配原则分别对岩体与锚固体的下压荷载进行计算，承台下锚杆分担的下压荷载为：其中：ac为承台面积；n为群锚基础的下压荷载；nm为承台下锚杆分担的下压荷载；f为承台下岩土体单位面积的承载力；am为锚杆的净截面面积，由锚杆根数与单锚杆的横截面积相乘得到；ec、em分别为岩土体与锚固体的弹性模量。当承台下锚杆分担的下压荷载满足要求时，承台面积即可确定。因此，群锚杆基础的承台面积的计算步骤如下：(1)根据锚固体和地基的相关参数、初定的承台尺寸，确定锚固体荷载分配比例，进而确定承台下锚杆分担的下压荷载nm；(2)结合地基承载力特征值f进行下压荷载验算、承台尺寸复核及调整。现以某典型中风化岩石地质条件下的锚杆基础设计为例，其岩体参数如下表1所示。表1：岩体特性弹性模量泊松比剪切模量单轴饱和抗压强度浆岩界面极限粘结强度mpa/mpampampa150000.285.8630～606锚杆基础锚筋采用36mm直径hrb400的螺纹钢，其弹性模量为200gpa；锚固浆体强度等级采用c30，其弹性模量及泊松比分别取20gpa和0.2；根据本发明提出的单锚杆极限上拔承载力实际值的计算方法计算如下表2所示。表2：单锚杆极限上拔承载力实际值计算为了验证本发明设计方法的有效性和优势，将同样边界条件下的数值模拟结果、规范设计结果及类似条件下锚杆基础真型试验结果进行对比，如下表3所示。表3：上拔承载力计算结果对比注：《架空输电线路基础设计技术规程》dl/t5219-2014由表3可知，在上述地质条件下，采用本发明实例提供的设计方法，计算的单锚杆极限上拔承载力实际值要比原设计方法大约10％；同时数值模拟的结果比两种设计公式计算结果均要大，这是由于数值模拟过程中存在诸多理想假设所导致的；显然，采用本发明提出的公式计算的单锚杆极限上拔承载力实际值与基础真型试验结果真实值更为接近。而对于群锚基础承台尺寸的确定，现以某强风化页岩群锚基础为例，页岩弹性模量取3gpa，锚固体直径100mm，锚筋为4根，承台高度为1m；当不考虑锚固体的承压作用时，下压荷载全部由承台底岩土体承担，根据承台底岩土体承载力计算得到承台平面最小尺寸为1.5m×1.5m；根据本发明的思想，考虑承台底岩土体的下压作用，经过试算，当承台平面尺寸取为1.4m×1.4m时，锚固体荷载分配系数为0.159，同时承台底岩土体的压下承载力也能满足要求；与以前的做法相比，采用本发明的方法可以使承台的混凝土体积减小约13％，在锚杆基础大面积使用的条件下，本发明提出的思想和方法具有显著的经济效益和社会效益。以上仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本领域的技术人员在本发明所揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。本说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。当前第1页12