改进布谷鸟搜索算法优化极限学习机的网络流量预测方法与流程

本发明涉及智能计算技术领域，具体涉及一种改进布谷鸟搜索算法优化极限学习机的网络流量预测方法。

背景技术：

伴随着物联网、泛在网络等概念的提出，下一代互联网骨干网各节点之间、局域网各节点之间的网络流量数据将呈现大幅度增长，互联网流量即将迈入大数据时代。在大数据流量背景下，网络业务类别的急剧增加导致网络流量性质发生改变，传统的流量模型已不适用于当今乃至下一代互联网流量的分析与预测，因此对智能网络流量预测的研究势在必行。elm(extremelearningmachine，极限学习机)是人工智能神经网络的一种，具有结构简单、训练速度快、调节参数少和泛化能力强等优点，并且有极强的非线性逼近能力，作为bp神经网络的改进，克服了bp神经网络需要设置大量的网络训练参数的缺陷，并且容易产生局部最优解的问题，因此可以用于刻画影响短期电力负荷预测的非线性相关因素演变，目前已广泛应用于变压器顶部油温预测、雾霾预测、月降雨量和热带气候预测、湍流地球物理流量、土壤湿度预测、风电预测、流量预测等场合。

但是在实际应用中，由于其部分网络权值是随机初始化的，每次初始化后得出的模型预测结果不同。从而导致极限学习机网络的预测时间较长，且不能保证其预测稳定性和精度。

技术实现要素：

针对现有技术中存在的缺陷，本发明的目的在于提供一种改进布谷鸟搜索算法优化极限学习机的网络流量预测方法，提高极限学习机的网络流量预测准确率。

为达到以上目的，本发明采取的技术方案是：一种改进布谷鸟搜索算法优化极限学习机的网络流量预测方法，包括以下步骤：

获取初选集合，所述初选集合包括多个寄生巢，所述寄生巢指的是巢里面的鸟蛋，每个所述寄生巢的鸟蛋表示极限学习机的一组初始权值和阈值；

计算每个寄生巢的适应度值，所述适应度值为极限学习机的最小预测误差，将当前种群中适应度值最优的寄生巢保留至下一代；

通过变量j选择不同的更新算子对当前每个寄生巢中的鸟蛋进行更新求解；

进行局部搜索，将改进的寄生巢的数量保存在变量se中；基于概率pa选择最差的寄生巢；

进行全局搜索，在变量se中保存改进的寄生巢的数量；

根据局部搜索、全局搜索后更新的解的数量se调整性能指标pm；

根据pm判断使用snap模式或drift模式计算pa的值；

判断更新次数是否达到迭代次数，若是，根据更新后的适应度值最小的寄生巢的位置确定所述极限学习机的最优初始权值和阈值；若否，返回继续寻找适应度值最小的寄生巢。

在上述技术方案的基础上，在所述获取初选集合之前，还包括以下步骤：

对每个寄生巢进行编码，对于一个包含m个寄生巢的种群，其种群规模即为m，每个寄生巢的维度即编码长度为d；

则每寄生巢xi表示为(xi1,xi2,...,xid)(i＝1，2，...，m)；

其中，d维空间中的寄生巢用一个m×d矩阵xm×d表示，分量xij表示第i个寄生巢的第j维的决策值，每个寄生巢代表一组灰色神经网的权值和阈值。

在上述技术方案的基础上，所述计算每个寄生巢的适应度值，具体包括：

根据适应度函数公式计算每个所述寄生巢的适应度值，所述适应度函数公式为：

其中，ok为极限学习机第k个节点的实际输出，dk为极限学习机第k个节点的期望输出，q为网络的输出节点数，x代表其中一个个体。

在上述技术方案的基础上，所述通过变量j选择不同的更新算子对当前每个寄生巢中的鸟蛋进行更新求解，具体包括：

判断所述均匀分布的随机数p是否小于基于概率的变量j；若是则根据鸟蛋自身的信息和莱维飞行策略来发现新的解，即根据公式(2)进行更新；若否，则判断所述均匀分布的随机数p是否小于1减去基于概率的变量j；若是，则搜索自身周围区域和莱维飞行策略来搜索空间中xij所在位置，即根据公式(3)进行更新；若否，则使用信息共享策略和莱维飞行策略进行更新，即根据公式(4)进行更新；

其中，表示点对点乘法，β是莱维飞行指数，a0是步长比例因子，和是随机选择的两个不同解。

在上述技术方案的基础上，所述莱维飞行策略，其基本公式为：

a>0为步长参数，与所考虑问题的尺度成比例；u和v的服从均值和方差为0正态分布，其中g为标准的gamma函数，如式(8)所示：

在上述技术方案的基础上，所述进行局部搜索，具体包括：

计算当前更新后的每个寄生巢的适应度值，求得局部最小值。

在上述技术方案的基础上，所述基于概率pa选择最差的寄生巢，具体包括：

判断所述均匀分布的随机数p是否小于基于概率的变量j；若是则使用信息共享策略进行更新，即根据公式(9)进行更新；若否，则判断所述均匀分布的随机数p是否小于1减去基于概率的变量j；若是则搜索自身周围区域并吸引其到搜索空间中xij所在位置，即根据公式(10)进行更新；若否，则根据鸟蛋自身的信息来进行更新，即根据公式(11)进行更新；

在上述技术方案的基础上，所述根据局部搜索、全局搜索后更新的解的数量se调整性能指标pm，具体包括：

pm＝se/(2*n)(12)。

在上述技术方案的基础上，所述根据pm判断使用snap模式或drift模式计算pa的值，具体包括：

使用性能度量pm作为控制参数，决定性能增强或保持不变时是继续使用drift模式搜索，或切换到snap模式，并通过式(13)更新pa：

其中，±ω是用来增加或减少pa的速率；

判断所述pm是否小于0.5；若是，则使用snap模式，pa取更小的值；若否，则使用drift模式，pa取更大的值。

在上述技术方案的基础上，所述根据更新后的适应度值最小的寄生巢的位置确定所述极限学习机的最优初始权值和阈值之后，还包括以下步骤：

将更新后的适应度值最小的寄生巢对应的最优初始权值和阈值，作为极限学习机的初始连接权值和阈值进行训练；

设置隐含层节点数，使用训练样本训练elm模型，计算网络误差，计算网络预测输出和期望输出的误差；

调整网络权值，根据各层之间的误差，调整各层之间的连接权值和阈值；

使用测试样本测试网络；

计算测试误差及效果评价。

与现有技术相比，本发明的优点在于：

本发明提供一种改进布谷鸟搜索算法优化极限学习机的网络流量预测方法，采用实数编码表示每个寄生巢，采用snap-drift布谷鸟搜索算法对极限学习机进行参数优化，实现预测误差更小，预测时间更短。网管人员可以依据更高预测精度的预测结果采取相应措施避免故障发生，减小网络故障带来的破坏，增强网络的可生存性，降低维护成本。本发明执行snap-drift布谷鸟搜索算法给鸟蛋分配解、拒不搜索、概率搜索选择最差寄生巢、全局搜索、更新pm和更新pa等操作，可知算法寻优能力强，计算复杂度低，计算速度快，收敛速度快，能够进行全局搜索，有跳出局部最优解的能力。

附图说明

图1为本发明实施例的改进布谷鸟搜索算法优化极限学习机的网络流量预测方法的流程图；

图2为本发明实施例的改进布谷鸟搜索算法优化极限学习机的极限学习机测试的流程图。

具体实施方式

以下结合附图对本发明的实施例作进一步详细说明。

本发明实施例提供一种改进布谷鸟搜索算法优化极限学习机的网络流量预测方法，包括以下步骤：

获取初选集合，所述初选集合包括多个寄生巢，所述寄生巢指的是巢里面的鸟蛋，每个所述寄生巢的鸟蛋表示极限学习机的一组初始权值和阈值；

计算每个寄生巢的适应度值，所述适应度值为极限学习机的最小预测误差，将当前种群中适应度值最优的寄生巢保留至下一代；

通过变量j选择不同的更新算子对当前每个寄生巢中的鸟蛋进行更新求解；

进行局部搜索，将改进的寄生巢的数量保存在变量se中；基于概率pa选择最差的寄生巢；

进行全局搜索，在变量se中保存改进的寄生巢的数量；

根据局部搜索、全局搜索后更新的解的数量se调整性能指标；

根据判断使用snap模式或drift模式计算pa的值；

判断更新次数是否达到迭代次数，若是，根据更新后的适应度值最小的寄生巢的位置确定所述极限学习机的最优初始权值和阈值；若否，返回继续寻找适应度值最小的寄生巢。

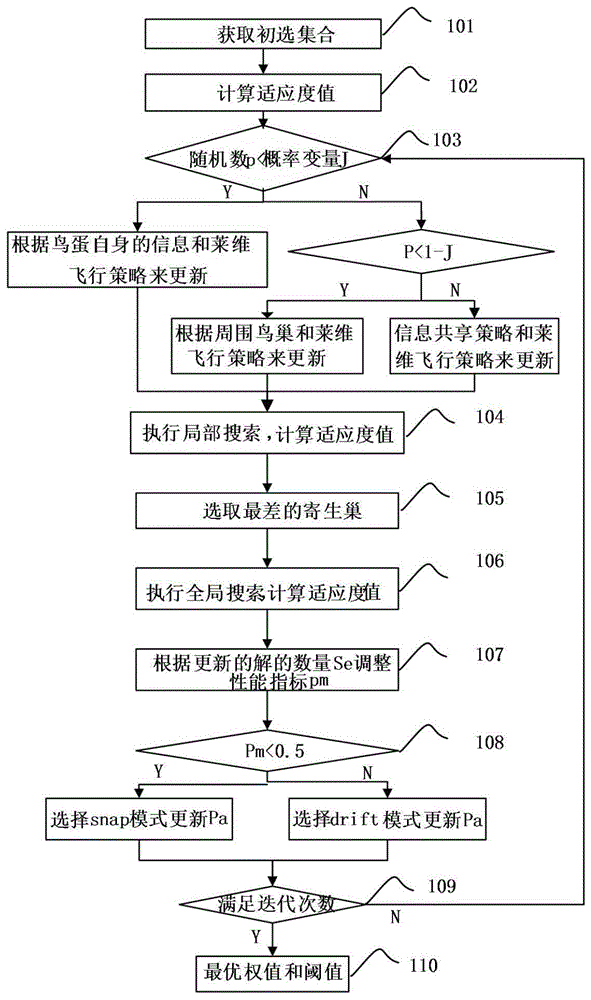
图1为本发明实施例的改进布谷鸟搜索算法优化极限学习机的网络流量预测方法的流程图，如图1所示，包括以下步骤：

步骤101：获取初选集合，所述初选集合包括多个寄生巢，所述寄生巢指的是巢里面的鸟蛋，每个所述寄生巢的鸟蛋表示极限学习机的一组初始权值和阈值，将其带入到极限学习机便可得改进后的极限学习机模型；

可选的，在所述获取初选集合之前还包括：

对每个寄生巢进行编码：对于一个包含m个寄生巢，种群规模即为n，每个寄生巢的维度即编码长度为d，，则每寄生巢xi表示为(xi1,xi2,...,xid)(i＝1，2，...，m)，其中，d维空间中的寄生巢可用一个m×d矩阵xm×d表示，分量xij表示第i个寄生巢的第j维的决策值，则每个寄生巢个体代表一组灰色神经网了的权值和阈值，将权值和阈值运用到极限学习机中，即极限学习机的预测模型就确定下来了。

步骤102：计算每个寄生巢的适应度值，根据适应度值对每个寄生巢进行评价，将当前种群中最好的寄生巢保留至下一代；所述适应度值为极限学习机的最小预测误差。适应度函数公式为：

其中，ok为极限学习机第k个节点的实际输出，dk为极限学习机第k个节点的期望输出，q为网络的输出节点数，x代表每一个个体。根据误差e(x)不断调节各个节点之间的权值和阈值对极限学习机进行训练，以达到寻找最优一组权值和阈值的目的。

步骤103：则通过变量j选择不同的更新算子对当前每个寄生巢中的鸟蛋进行更新求解；

判断所述均匀分布的随机数p是否小于基于概率的变量j；若是则根据鸟蛋自身的信息和莱维飞行策略来发现新的解，即根据公式(2)进行更新；若否，则判断所述均匀分布的随机数p是否小于(1－基于概率的变量j)；若是则搜索自身周围区域和莱维飞行策略来搜索空间中xij所在位置，即根据公式(3)进行更新；若否，则使用信息共享策略和莱维飞行策略进行更新，即根据公式(4)进行更新。

其中，表示点对点乘法，β是莱维飞行指数，a0是步长比例因子，和是随机选择的两个不同解。其中莱维飞行基本公式为：

b>0为步长参数，它与所考虑问题的尺度成比例。u和v的服从均值和方差为0正态分布，其中g为标准的gamma函数。如式(8)所示：

步骤104：局部搜索，随机选择一个寄生巢并使用莱维飞行和新合并的信息共享算子，接下来，将改进解的个数保存在变量se中；

步骤105：基于概率pa来选择最差的寄生巢；

判断所述均匀分布的随机数p是否小于基于概率的变量j；若是则使用信息共享策略进行更新，即根据公式(9)进行更新；若否，则判断所述均匀分布的随机数p是否小于(1－基于概率的变量j)；若是则搜索自身周围区域并吸引其到搜索空间中xij所在位置，即根据公式(10)进行更新；若否，则根据鸟蛋自身的信息来进行更新，即根据公式(11)进行更新。

步骤106：全局搜索，对于每个废弃的寄生巢，使用简单的随机游走算法和新的合并信息共享算子更新寄生巢，接下来，在变量se中保存改进的寄生巢的数量；

步骤107：使用经过局部和全局搜索后根据更新的解的数量se调整性能指标pm；

pm＝se/(2*n)(12)

步骤108：根据pm判断使用snap模式或drift模式计算pa的值；

sdcs使用性能度量pm作为控制参数，决定性能增强(或保持不变)时是否继续使用drift模式搜索，或切换到其他搜索模式以提高搜索能力。因此，性能度量pm为提出的算法找到搜索模式之间的平衡点提供了必要的条件。考虑到上述事实，sdcs通过式(13)更新pa:

其中，±ω是用来增加(或减少)pa的速率。当sdcs性能较差时，选择snap模式，pa取较小的值。否则，选择drift模式，pa取较大的值。

步骤109：判断更新次数是否小于所述迭代次数；

若是，则返回步骤103；若否，则去到步骤110；

步骤110：找到当前最佳适应度值，即极限学习机最优初始权值和阈值。

如图2所示，找到当前最佳适应度值后，还包括以下步骤：

步骤111：根据更新后的适应度值最小的寄生巢即最优权值和阈值，将其作为极限学习机的初始连接权值和阈值进行训练，即开始计算每一层的输出。

步骤112：设置隐含层节点数，使用训练样本训练elm模型，计算网络误差，计算网络预测输出和期望输出的误差；

步骤113：调整网络权值，根据各层之间的误差，调整各层之间的连接权值和阈值；

步骤114：使用测试样本测试网络；

步骤115：计算测试误差及效果评价。

本发明实施例采用的snap-drift布谷鸟搜索算法(snap-driftcuckoosearch，sdcs)，cs结合了采用莱维飞行的布谷鸟专性育雏寄生的思想来求解优化问题。参考探索-开发平衡的最优收缩定理，从而找到上述问题的较优的解。即最优优化器应该考虑关于当前问题的最有用的信息。采用基于积累信息的适应度函数来调节一个权衡，引入了一种新的cs变体，即snap-drift布谷鸟搜索(snap-driftcs，sdcs)，通过学习技术周期性地获取问题的适应度函数信息，从而优化问题的寻优搜索行为。事实上，此算法使用了一种强化学习的形式，在两种snap和drift模式之间进行切换。在snap模式下，sdcs增强了全局搜索能力，以缓解早熟收敛问题。在drift模式下，局部搜索的概率增加，以提高收敛速度。sdcs使用了一种概率适应；其中，算法性能随着被适应的概率的提高而降低。为此，sdcs推出了新的搜索，分别增强了snap和drift模式下的全局和局部搜索能力，能够跳出局部最优，从而达到全局搜索的目的，并且该算法的计算速度也很快。

显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。这样，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。