一种空间对象形态切割的方法与流程

本发明涉及一种空间对象形态切割的方法，属于空间图形处理技术领域。

背景技术：

切割要素是矢量图生产中经常用到的一种操作，面要素会由分割线分割出多个要素，要素的属性表也要复制原来要素的一份，都是矢量地图生产人员经常用到的要素编辑的操作，例如矢量地图根据行政区域划分进行切割。

原生qgis切割算法在处理带有大量内环(内洞)的复杂多边形时切割效率低下，且偶尔会出现崩溃的情况，原生算法在处理大量内洞时使用了大量的空间操作，导致算法效率低下。

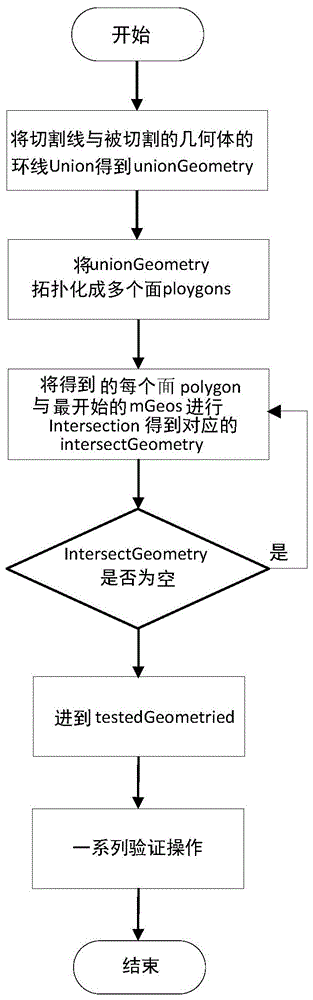
如图1所示的qgis切割算法流程图，该方法首先得到mgeos(被切割的几何体)的boundary(包括外边界和内洞边界)，即将二维的面降维成环线。然后将环线与割线进行geounion操作，得到联合后的uniongeometry。再将得到的uniongeometry拓扑化成面，此时所有闭合的环线都会拓扑化成为一个面，mgeos的内洞也会拓扑化成为一个面，因此得到多个面，变量名为unionpolygons。再对unionpolygons进行遍历，将其中每个闭合环线形成的面即polygon分别与mgeos进行geosintersection(相交或求交集)操作，得到对应的intersectgeometry，若ploygon为内洞或者切线在mgeos外部形成的冗余多边形(冗余面)，得到的intersectgeometry为nullptr(为空)，则认为是无效面并跳过；若intersectgeometry不为空，分别计算intersectgeometry和对应的ploygon的面积，若两者面积之比在[0.99,1.01]范围内，则证明这个面为有效面。最后将所有有效面导入到testedgeometried向量内，并对其进行一系列检测，若切割成功，则算法结束。

该算法适用于小数据量，能够处理所有特殊切割的情况。但是，对于复杂数据(特别是dem数据矢量化的复杂数据)每一个内洞都需要与mgeos进行intersection(相交)操作，导致时间复杂度上升过快，无法满足生产人员要求。

技术实现要素：

本发明的目的是提供一种空间对象形态切割的方法，用以解决现有切割算法效率低下的问题。

为实现上述目的，本发明的方案包括：

本发明的一种空间对象形态切割的方法，包括如下步骤：

1)得到被切割几何体的外环线和内环线；所述外环线为被切割几何体的最外层的一个或多个封闭轮廓线，所述内环线为处于外环线内部的一个或多个封闭轮廓线；

2)找到所有与切割线相交的内环线，并与外环线构成第一图形；所述第一图形包括外环线和与切割线相交的内环线之间的区域；

3)第一图形与切割线合并后拓扑化，得到多个面形成的图形，仅保留其中的有效面后得到仅由有效面形成的切割图形；每个闭合的线形成一个面，处于所述第一图形内的面为有效面；

4)将不与切割线相交的内环线按照对应位置回填入所述切割图形中；

5)输出切割图形。

现有技术的矢量图切割算法对于带有大量内洞且具有复杂外环线的图形处理速度较慢，因此本发明的改进切割算法主要规避了带有大量内洞的复杂多边形的多次空间关系运算，仅对与切割线相交的内洞和外环进行操作，得到一个中间图形，未与切割线相交的内洞无需过多处理，直接与中间图形相交即可完成切割算法，避免了大量空间操作，提升了算法效率，降低了错误率。

进一步的，步骤3)中，筛选有效面的方法为，对应获得所述切割图形中每个面中至少一个内点，若内点落入所述第一图形内，则该内点所在的面为有效面。

通过内点与被切割几何体的位置关系判断面是否为非内洞、非冗余多边形的有效面，算法简单可靠易于实现。

进一步的，步骤4)中，回填不与切割线相交的内环线的方法为，找出所有不与切割线相交的内环线，并与被切割几何体的外接矩形构成第二图形；在找出所有有效面后，根据所述外接矩形与所述外环线的位置关系，将第二图形与仅保留有效面的切割图形相交。

使用mgeos的外包矩形和不相交的内洞创建出多边形，便于实现不与切割线相交的内环线与有效面的位置关联，算法简单准确。

附图说明

图1是现有技术的qgis切割算法流程图；

图2是本发明的空间对象形态切割方法流程图；

图3(a)是被切割的几何体示意图1；

图3(b)是被切割的几何体示意图2；

图4是一个实例中的被切割的几何体示意图；

图5(a)是实例中相交图形示意图；

图5(b)是实例中非相交图形示意图；

图6是实例中相交图形与切割线合并后拓扑化的示意图；

图7是实例中有效多边形和非相交图形相交示意图。

具体实施方式

下面结合附图对本发明做进一步详细的说明。

如图2所示的本发明的空间对象形态切割方法流程图，本发明的方法包括如下步骤：

1)：得到mgeos(被切割的几何体)的外环线和内环线(内洞holes)；举例来说，如图3(a)所示，被切割的几何体mgeos为区域①(三角形图形1区域内除去椭圆图形2形成的内洞②区域的剩余部分)，两条虚线3为两条切割线，本步骤中得到外环线为图形1的边线和内环线为椭圆2的椭圆线。

2)：将内环线分为与切割线相交的内环线(intersectholes)和与切割线不相交的内环线(nointersectholes)；图3(a)中所示的被切割的几何体仅有一个内环线，即与切割线相交的内环线椭圆2，没有不与切割线相交的内环线。

3)：与切割线不相交的内环线与mgeos的外接矩形创建一个图形boxwithhole，与切割线相交的内环线与外环线创建另一个图形ringwithhole；mgeos外接矩形可以为能容纳下被切割的几何体的最小矩形；以图3(a)和图3(b)中的mgeos为例时，因没有与切割线不相交的内环线，因此得到的图形ringwithhole依然为最初的被切割的几何体mgeos的区域①，图形boxwithhole为空。

4)：图形ringwithhole与切割线合并得到合并几何体uniongeometry，再将合并几何体uniongeometry进行拓扑化，得到多个面的图形multiploygon(每个面在图形中的位置基于图形ringwithhole沿用和保留)；在拓扑化的时候，所有闭合的边都会形成一个面，因此以图3(a)和图3(b)中的mgeos为例，如图3(b)所示，multiploygon包括面a、b、c、d，面d为因切割线3而产生的冗余多边形。

5)：循环遍历multiploygon中每一个面，得到其中的一个面后，进而得到该面内的一点，判断该面中的内点是否在图形ringwithhole内；显然面b内的点落入图形ringwithhole中的内洞②中，因而未落入图形ringwithhole内；面d为切割线3在mgeos外围成的冗余多边形，因而也未落在图形ringwithhole内。

6)：如果内点不在图形ringwithhole内，则对应面无效；如果内点在多边形ringwithhole内，则对应面为有效面；面b、d为无效面，多边形a、c为有效面。

7)：得到有效面之后将仅带有全部有效面的图形(无效面在外环线内的形成内洞，在外环线外无效面则直接丢弃)与图形boxwithhole进行相交操作，回填内洞；本步骤前可先判断多边形boxwithhole中是否为空(为空即为图形中没有内环线)，若为空可直接跳过本步骤。

8)：有效面或者有效面和图形boxwithhole的交集进入检测集testedgeometry中，并完成一系列检测操作，算法结束。

下面再以一个实例对本发明的方法进行说明。

如图4所示的待切割几何体mgeos③，由图形4和和其中的空洞5、内洞6构成。虚线7为切割线。

首先得到mgeos外环线和内环线，得到的外环线为4，内环线为5和6；遍历所有内环线，寻找与切割线7相交的所有内环线，以及与切割线7不相交的内环线，即将内环线区分为与切割线7相交的和不相交的，得到切割线7相交的内环线5及与切割线7不相交的内环线6。

与切割线7相交的所有内环线即内环线5(内洞5)，和外环线4形成如图5(a)所示的相交图形；与切割线7不相交的所有内环线即内环线6(内洞6)，和外环线4的外接矩形8形成如图5(b)所示的非相交图形。

将相交图形与切割线相交，并将相交后得到的图形拓扑化，如图6所示，得到包括多个面的切割图形，其中相交图形除去内洞5的剩余部分被切割线7分割为面e、h，同时内洞5被切割线7分割为面f、g，最终切割图形包括面e、f、g、h。

遍历切割图形中的面e、f、g、h，并对应获得每个面内的一点，判断每个点是否在如图5(a)所示的相交图形内，面e、h中的点落入相交图形，面f、g中的点因落入内洞5而未落入相交图形。内点落入相交图形的对应面为有效面，未落入相交图形的对应面为无效面。

因非相交图形不为空，因此仅保留有效面的切割图形和如图5(b)所示的非相交图形进行相交操作，将内洞6按照外接矩形8和外环线4的对应位置关系回填入面h中，并在检测后最终得到如图7所示的切割后的图形，图形包括切割后的区域e、h。