概率有限状态机变异测试用例生成方法与流程

文档序号：22928778发布日期：2020-11-13 16:25阅读：472来源：国知局

本发明涉及软件测试技术领域，更具体地说，本发明涉及一种概率有限状态机变异测试用例生成方法。

背景技术：

有限状态机是一种描述软件需求的形式规格说明描述工具，具有精确性、可推导性和可验证性等优点。因此，基于有限状态机的测试特别是其测试用例生成技术被广泛研究

。国内学者在该方面也进行了深入的研究，张涌^[2]等提出一种wp方法的改进方法，使用该方法在有限机状态数目较大时可以产生相对较少的测试输入序列数目。变异测试作为一种面向缺陷的软件测试技术已经得到广泛的应用^[3]。

概率有限状态机是确定有限状态机的推广，已成为建模和分析复杂的非线性动力系统的一个有力工具^[4，5]，在计算语言学^[6]、模式识别^[7]、序列数据检测^[8]、机器人运动识别^[9]及程序理解^[10]等方面都有着重要的应用.针对有限状态机的变异测试问题，fabbri等^[11]首先对有限状态机的变异测试进行了讨论，定义了有限状态机的9种变异操作，并对基于w方法和tt方法产生的测试用例杀死状态机变异体的效率进行了比较并应用于iso传输协议的测试，结果表明基于有限状态机的变异测试能够有效的发现协议的错误。之后，fabbri等^[12]开发了基于有限状态机变异测试的工具并运用于c程序的测试。f.beli等^[13]对基于事件顺序图、有限状态机及状态图的变异体的错误检测能力进行了比较。timo等^[14]提出了符号输入有限状态机(sifsm)及其不合格变量检测方法。petrenko等^[15]探讨了约束满足问题下变异覆盖率检验的分析方法。r.m.hierons等^[16，17]讨论了概率有限状态机的变异测试，定义了概率有限状态机的4种变异操作，给出了变异体是否与原状态机等价的判定方法.若变异体与原状态机不等价，则可求解可区分pfsm及其变异体的输入序列。该方法的不足在于：(1)由于pfsm变异体数量巨大，因此逐一对每个变异体与原pfsm判定是否等价后再求解测试序列导致时间开销大；(2)不能通过测试的输出序列确定变异体的变异原因及位置。r.m.hierons在其论文的结论中指出，关于概率有限状态机的变异测试仍有两个重要问题尚待解决：(1)如何有效地生成杀死概率有限状态机变异体的测试序列；(2)在给定的概率误差范围内如何有效地减少测试序列对变异体的测试次数。另外，文献[16，17]没有给出迁移丢失、改变输入及改变输出等等其它变异体测试用例的生成方法，亦没有提供相关的辅助测试工具并通过实验来验证所提出方法的正确性和有效性。

上述的文献1～17分别对应为：

[1]liupan，miaohui-kou，zenghong-wei，meijia.dfsm-basedminimumtestcosttransitioncoveragecriterion.journalofsoftware，2011，22(77):1457-1474(inchinese).

刘攀，缪淮扣，曾红卫，梅佳.确定性有限状态机的最小测试成本迁移覆盖准则.软件学报，2011，22(77):1457-1474.

[2]zhangyong，qianqiu-le，wangyuang-feng.testsequencesselectionbasedondeterministicfinite-statemachines.journalofcomputerresearchanddevelopment，2002，39(9):1144-1150(inchinese).

张涌，钱秋乐，王渊峰.基于确定有限状态机的测试序列选取.计算机研究与发展，2002，39(9):1144-1150.

[3]shanjin-hui，gaoyou-feng，liuming-hao.anewapproachtoautomatedtestdatagenerationinmutationtesting.journalofcomputer，2008，31(6):1025-1034(inchinese).

单锦辉，高友峰，刘明浩等.一种新的变异测试数据自动生成方法.计算机学报，2008，31(6):1025-1034.

[4]xiezheng-wei，zhaiying，dengpei-min，yizhong.algebraicpropertiesofprobabilisticfinitestateautomata.journalofcomputer，2013，50(12):2691-2698(inchinese).

谢正卫，翟莹，邓培民，易忠.概率有限状态自动机的代数性质.计算机研究与发展，2013，50(12):2691-2698.

[5]vidal.e；thollard.f；higuera.c.probabilisticfinite-statemachines-parti.ieeetransactionsonpatternanalysisandmachineintelligence，2005，27(7):1013-1025.

[6]m.mohri.finitestatetransducersinlanguageandspeechprocessing.computationallinguistics，1997，23(3):269-311.

[7]wen，yicheng；ray，asok.vectorspaceformulationofprobabilisticfinitestateautomata.journalofcomputerandsystemsciences，2012，78(4):1127-1141.

[8]shen，jun；yang，minhua；zou，bin；outlierdetectionofairtemperatureseriesdatausingprobabilisticfinitestateautomata-basedalgorithm.complexity，2012，17(5):48-57.

[9]adenis，patrick；wen，yicheng；ray，asok.aninnerproductspaceonirreducibleandsynchronizableprobabilisticfinitestateautomatamathematicsofcontrolsignalsandsystems，2012，23(4):281-310.

[10]chenhua，wangchan，chenchun.programcomprehensionusinginformationretrievalandprobabilisticfinite-stateautomata.journalofzhejianguniversity(engineeringscience)，2008，42(12):2108-2111(inchinese).

陈华，王灿，陈纯等.利用信息检索和概率有限自动机的程序理解.浙江大学学报(工学版)，2008，42(12):2108-2111.

[11]s.c.p.f.fabbri，j.c.maldonado.mutationanalysistestingforfinitestatemachines.proceedingofthe5thinternationalsymposiumonsoftwarereliabilityengineering，monterey，california，6-9november1994，pp.220-229.

[12]s.c.p.f.fabbri，j.c.maldonado.protem/fsm:atooltosupportfinitestatemachinevalidationbasedonmutationtesting.proceedingofthe19thinternationalconferenceofthechileancomputersciencesociety，talca，chile，11-13november1999，p.96.

[13]f.belli，c.j.budnik.basicoperationforgeneratingbehavioralmutants.proceedingofthe2ndworkshoponmutationanalysis.raleigh，northcarolina:ieeecomputersociety，2006，p.9.

[14]nguenatimoo.，petrenkoa.，rameshs.multiplemutationtestingfromfinitestatemachineswithsymbolicinputs.in:yevtushenkon.，cavallia.，yenigünh.(eds)testingsoftwareandsystems.ictss2017.lecturenotesincomputerscience，vol10533.springer，cham，pp108-125.

[15]petrenkoa.，nguenatimoo.，rameshs.(2016)multiplemutationtestingfromfsm.in:alberte.，lanesei.(eds)formaltechniquesfordistributedobjects，components，andsystems.forte2016.lecturenotesincomputerscience，vol9688.springer，cham，pp222-238.

[16]r.m.hierons，m.g.merayo.mutationtestingfrommutationtestingfromprobabilisticfinitestatemachines.proceedingsofthe2ndtesting:academicandindustrialconferencepracticeandresearchtechnique.windsor，uk:ieeecomputersociety，10-14september2007:141-150.

[17]r.m.hierons，m.g.merayo.mutationtestingfromprobabilisticandstochasticfinitestatemachinesjournalofsystemsandsoftware，2009，82(11):1804-1818.

技术实现要素：

本发明的一个目的是解决至少上述缺陷，并提供至少后面将说明的优点。

本发明的另一个目的是提供一种概率有限状态机变异测试用例生成方法，针对概率有限状态机(probabilisticfinitestatemachine，简称pfsm)变异测试问题，定义了包括改变概率、改变输入、改变迁移目标状态、迁移丢失、增加输入等变异操作；在定义pfsm原始状态机基础上，根据各种变异操作的特点，利用pfsm原始状态机的测试用例集和假设检验方法提出杀死各种变异体的测试用例生成方法。

为了实现本发明的这些目的和其它优点，本发明提供一种概率有限状态机变异测试用例生成方法，包括：

定义pfsm原始状态机，并获得pfsm原始状态机的测试用例集；

再定义多种变异操作及对应的变异体；所述变异操作至少包括：改变概率、改变迁移目标状态；

利用假设检验方法从pfsm原始状态机的测试用例集中选出能够杀死对应变异体的测试用例，生成用于杀死变异体的测试用例集。

优选的是，所述的概率有限状态机变异测试用例生成方法中，概率有限状态机pfsm为一个五元组(s，s0，x，y，h)；

其中s是一个有限状态集；s0∈s为状态机的初始状态；x是一个有限输入符号集；y是一个有限输出符号集；h：s×x→s×y×(0，1]为迁移关系函数；

设s1，s2∈s，x∈x且y∈y，用(s1，x，y，s2，p)表示在状态s1下，当输入为x，则输出为y且从状态s1转移到状态s2的概率为p；同时满足对每个s∈s，x∈x都有其中p(s,x,y,s^*)为当pfsm在状态s下输入x时转移到s^*且输出y的概率；

定义函数pm：s×x→s×y×(0，1]如下：

从状态si始在输入序列的作用下，输出为而且转移到状态sj的概率其中：

fsm＝(s，s0，x，y，h-p)为pfsm的原始有限状态机，其中h-p为s×x→s×y，且fsm中存在迁移(s1，a，b，s2)当且仅当在pfsm中存在(s1，a，b，s2，p)；

根据基于wp方法的有限状态机测试用例生成算法，获得以下数据：

1)状态机各个状态s0，s1，…，sn-1的状态识别集合w0，w1，…，wn-1；

2)使状态机从初始状态转移到各个状态的输入序列集合即状态覆盖集合q＝{in0i|in0i为使状态机从初始状态转移到各状态的输入序列}；

3)迁移覆盖集合p；

4)测试用例集π。

针对wp方法：

定义：一组输入序列wi是一个识别状态集si当且仅当s中的每个状态sj(当i≠j)存在wi的输入序列，使得silp≠sjlp并且wi的任何子集都没有这个属性。

所有状态si的识别集wi的并集是一个特征集。

wp方法由两个阶段组成，目标如下：

阶段1：此阶段检测规约说明中定义的全部状态在实现中是可识别的，并检查每个状态ik能被序列wk识别；同时，检测从初始状态到这些状态的迁移输出和状态迁移是否正确。

阶段2：此阶段检测第一阶段未检测的其余全部的规约说明中定义的迁移。

wp方法进行如下具体操作：

1.确定一个迁移覆盖集p，其中包括一个状态覆盖集q；对于s的每个状态si，一个识别集wi被确定，w被定义为一组输入序列，至少包括所有wi的所有序列(即构建为wi的联合体)；集合wz称为w；需要注意的是，对集合p、q及wi的不同选择会产生不同的测试顺序。

2.q与w(即q.w)；规约说明的每种状态si在实现中用集合w检测；如果测试是成功的，即得s≈q.wi，在实现中的状态数i等于规约说明的集合s的状态数；由于wi是w的子集，因此使用集合wi识别实现中的状态iz是合适的；

3.第2阶段的测试序列包括不包含在q中的p所对应的wi，写为

其中wj是w和sj中sj的识别集的p到达；即s0-p→sj；在这个阶段检测其余的迁移；使用子集wj而不使用w识别转换的最终状态；如果i通过了两个阶段的测试，那么它就等于规范说明s。

文献2中的wp方法可以分为3个步骤：

①估计实现中的有限状态机中可能存在的状态数目的上界m.对某个有限状态机的正确实现应该与规约说明中的状态机具有相同的状态数目，这里的估计值m就是为了能够检测出某个有限状态机的实现中存在的额外状态，因此估计值m要大于或等于规约说明中的有限状态机中的状态数目n.估计值的选取是根据设计进行猜测得到的.

②检验在规约说明中的状态在实现中可被识别并验证其实现与规约说明中一致，同时从初始状态到这些状态所经历的状态迁移也被验证，并且检验实现中是否存在额外状态，该部分的测试输入序列可如下构造：

t1＝q.x[m-n].w.

③验证在上面没有被验证的状态迁移，测试输入序列可构造如下：

优选的是，所述的概率有限状态机变异测试用例生成方法中，针对改变概率的变异操作：

设定在概率有限状态机pfsm中，以状态si为起始且输入为xi1的迁移分别为：(si，xi1，yi1，si1，pi1)，(si，xi1，yi2，si2，pi2)，...，(si，xi1，yim，sim，pim)；

而在变异体pfsm^*中以状态si为起始且输入为xi1的迁移分别为：(si，xi1，yi1，si1，pi1^*)，(si，xi1，yi2，si2，pi2^*)，...(si，xi1，yim，sim，pim^*)；

并且至少pfsm中存在迁移(si，xi1，yij，sij，pij)而pfsm^*中存在迁移(si，xi1，yij，sij，pij^*)使得pij≠pij^*(1≤j≤m)，则pfsm^*为pfsm基于改变概率出的变异体，其中

由于在pfsm的原始状态机存在in0i∈q，因此在pfsm中存在从状态s0到si的一条路径path(s0，si)，设pfsm所经历的迁移序列如下：

(s0，xk1，yk1，sk1，pk1)(sm1，xk2，yk2，sk2，pk2)…(sm(n-1)，xkn，ykn，si，pkn)，该迁移序列对应的输入序列xk1.xk2…xkn记为path(s0，si)_in，输出序列yk1.yk2…ykn记为path(s0，si)_out，概率序列pk1pk2…pkn记path(s0，si)_pro，且满足path(s0，si)_in＝in0i∈q，其中q为基于wp方法所获得的pfsm原始状态机的状态覆盖集；

为了能够检测出pfsm^*中的迁移(si，xi1，yij，sij，pij^*)与pfsm中的迁移(si，xi1，yij，sij，pij)满足pij≠pij^*，需要通过测试表明：当被测的pfsm^*处于状态si且输入xi1时，输出yij的概率不等于pij；根据概率统计方法，可通过多次考察当被测的pfsm^*处于状态si当输入xi1时输出yij的次数来实现概率值的计算。如果状态si为初始状态，则以xi1作为输入多次运行状态机并记下输出yij的次数即可求出其概率值。若si不是初始状态，则首先使状态机从初始状态转移到状态si，然后才能输入xi1并进行统计；利用path(s0，si)_in输入序列可使状态机从初始状态转移到状态si，但在状态机中可能存在path(s0，si)_in＝path(s0，sj)_in，即把path(s0，si)_in运行于状态机，状态可能转移到si或sj；本发明所讨论的状态机是精简的，若path(s0，si)_in作用于状态机的输出序列为path(s0，si)_out则状态机必转移到si。为此，以path(s0，si)_in.xi1作为输入运行于pfsm^*若干次并统计输出序列的子串(该子串为输出序列除掉最后一个字符的字符串)等于path(s0，si)_out且输出序列最后一个字符为yij的次数sumij，即当pfsm^*处于状态si且输入xi1时输出yij的次数。

根据假设检验方法：若允许pij与pij^*的误差在ξ之间，即满足pij-ξ<pij^*<pij+ξ，则在path(s0，si)_in作用下到达状态si的样本数sum^*需满足下式1

其中p＝pk1×pk2×...×pkm，可信度取0.95，则z0＝1.96，由上式1可得式2：

sum^*≥3.8416p(1-p)/ξ²；

即当样本数sum^*≥3.8416p(1-p)/ξ²，如果满足pij-ξ<sumij/sum^*<pij+ξ，则得到pij与pij^*一致的结论，否则有pij≠pij^*；

使用一个二元组<path(s0，si)_in.xi1，sum^*>表示最多运行sum^*次输入序列path(s0，si)_in.xi1可杀死所述变异体pfsm^*并确定所改变概率的测试用例；

则用于杀死基于pfsm改变概率的变异体的测试用例集∏pro_change＝{<path(s0，si)_in.xij，sum^*>|i为pfsm任意状态si的下标值，xij为以状态si为起始迁移的输入}。

优选的是，所述的概率有限状态机变异测试用例生成方法中，判定pfsm^*中的迁移(si，xi1，yij，sij，pij^*)与pfsm中的迁移(si，xi1，yij，sij，pij)是否满足pij≠pij^*的具体步骤为：

输入：pfsm^*，path(s0，si)_in.xi1，ξ

输出：flag

step1.初始化：sumij＝0，sum^*＝0；

step2.若sum^*≥3.8416p(1-p)/ξ²，则转至step5，否则以path(s0，si)_in.xi1作为输入序列运行pfsm^*得到输出序列

step3.若则sum^*←sum^*+1且转至step4，否则转至step2；

step4.若则sumij←sumij+1且转至step2；

step5.若pij-ξ<sumij/sum^*<pij+ξ，则flag←1，否则flag←0。

优选的是，所述的概率有限状态机变异测试用例生成方法中，针对改变迁移目标状态的变异操作：

设定概率有限状态机pfsm的迁移t＝(si，x，y，si，p)在其变异体pfsm^*中为t^*＝(si，x，y，sk，p)，其中j≠k，即迁移t的目标状态si变成sk，则称pfsm*为pfsm基于改变迁移目标状态的变异体；

对于pfsm的原始有限状态机fsm，如果其迁移(si，x，y，si)的目标状态si变成sk，即得到一个与fsm不同的有限状态机，记为fsm^*，其中测试用例集π中存在输入序列使得其中分别为fsm，fsm^*在输入序列的作用下产生的一个输出序列；

根据有限状态机的定义可知若fsm与fsm^*唯一的不同之处在于fsm的迁移t＝(si，x，y，si)而在fsm^*中为对位于该迁移则为t^*＝(si，x，y，sk)，除此之外fsm与fsm^*没有任何不同，则要使得输入序列满足该输入序列在fsm中必然经过迁移t＝(si，x，y，si)而在fsm^*中必然经过t^*＝(si，x，y，sk)，即在输入序列的作用下从初始状态开始一定要转移到状态si，然后从该状态经过迁移t或t^*。因此，若输入序列满足则存在使得其中为的头。

通过以下方法在测试用例集π中到杀死变异体的输入序列

首先在π中找出头部为path(s0，si)_in的任一字符串的输入序列构成集合ω，然后在ω中找出满足的输入序列

由于ω中的输入序列越长则的可能性越大，另一方面其测试的代价也更高，为此定义输入序列优先值如式3：

其中为输入序列的长度，maxlen为ω中最长输入序列的长度值，α∈(0，1)为序列长度在优先值中的权重；ω中优先值大的输入序列将被优先运行于fsm^*以检测该序列是否为杀死变异体的输入序列；

其中，杀死变异体的测试序列的具体求解方法为：

输入：pfsm的原始状态机fsm及被变异迁移t＝(si，x，y，si，p)

输出：杀死变异体pfsm^*的测试用例

s1.生成测试用例集π；

s2.

s3.对ω中的序列按如下方式进行排序：

若则把排在前面，其中maxlen为ω中最长序列的长度值，

s4.对已经排序的ω，从ω的第一个序列开始，把序列分别作用fsm与fsm^*，直到有序列使得(fsm，xkill)≠(fsm^*，xkill)。

优选的是，所述的概率有限状态机变异测试用例生成方法中，还包括改变输入的变异操作，针对改变输入的变异操作：

设定在概率有限状态机pfsm中，分别用(si，xi1^*，yi1，si1，pi1)，(si，xi1^*，yi2，si2，pi2)，…，(si，xi1^*，yim，sim，pim)替换pfsm的(si，xi1，yi1，si1，pi1)，(si，xi1，yi2，si2，pi2)，…，(si，xi1，yim，sim，pim)而得到pfsm^*，即以状态si为起始且输入为xi1的迁移被输入xi1^*所替换，则pfsm^*为pfsm基于改变输入的变异体，其中xi1≠xi1^*；

根据变异操作可知，如果pfsm^*是分别用(si，xi1^*，yi1，si1，pi1)，(si，xi1^*，yi2，si2，pi2)，…，(si，xi1^*，yim，sim，pim)替换pfsm的(si，xi1，yi1，si1，pi1)，(si，xi1，yi2，si2，pi2)，…，(si，xi1，yim，sim，pim)得到的概率有限状态机，则当pfsm^*处于状态si时在xi1作用下的输出为空，即输出字符串的长度为0，而当pfsm处于状态si时在xi1作用下的输出为yi1，yi2，…，yim中的某个字符，其长度为1；为了能够断定概率有限状态机以状态si为起始且输入为xi1的迁移没有被其它输入所替换，按照假设检验方法，设定一个很小的ω，只要能够说明当状态机处于状态si时在xi1作用下输出字符串长度为1的概率接近1-ω则可认为以状态si为起始且输入为xi1的迁移没有被其它输入所替换，否则将认为其输入被改变；为此，以path(s0，si)_in.xi1作为测试用例反复运行于pfsm^*，直到每个输出序列的子串与path(s0，si)_out相等的次数sum^*≥3.8416ω(1-ω)/ξ²并统计在这些输出序列中其长度为|path(s0，si)_in.xi1|的个数之和sum，若1-ω-ξ<sum/sum^*<1-ω+ξ，则说明以si为起始状态且输入为xi1的迁移没有被其它输入所替换，否则其输入被改变；

如果确认了概率有限状态机以si为起始状态且输入为xi1的迁移被其它输入所替换，则接下来就要判定替换的是哪个输入字符；设在概率有限状态机pfsm中，以状态si为起始的所有迁移的输入集为x1，用path(s0，si)_in与x1中的每个字符x构成的输入序列path(s0，si)_in.x对pfsm^*进行测试，如果是x替换了xi1，则测试就会有1-ω-ξ<sum/sum^*<1-ω+ξ，即可知输入xi1被x所替换，因此即可杀死变异体；

用二元组<path(s0，si)_in.xi1，3.8416ω(1-ω)/ξ²>表示最多运行3.8416ω(1-ω)/ξ²次输入序列path(s0，si)_in.xi1可杀死基于改变输入的变异体pfsm^*并确定所改变输入的测试用例，则用于基于改变输入的变异体pfsm的测试用例集πin_change＝{<path(s0，si)_in.xij，3.8416ω(1-ω)/ξ²>|i为pfsm任意状态si的下标值，xij为以状态si为起始迁移的输入}。

优选的是，所述的概率有限状态机变异测试用例生成方法中，还包括增加输入的变异操作，针对增加输入的变异操作：

设在概率有限状态机pfsm中，以状态si为起始的所有迁移的输入集为x1，若pfsm的变异体pfsm^*以状态si为起始的所有迁移的输入集为x2且则称pfsm^*为pfsm基于增加输入的变异体；

若z∈x2而即增加了输入z，那么当pfsm^*处于状态si时在z作用下输出一个非空的字符，而当pfsm处于状态si时在z作用下则没有字符输出；根据假设检验方法可知，当以path(s0，si)_in.z作为测试用例运行于pfsm的次数最多达到sum^*时必然有输出序列yk1.yk2…ykn，而把path(s0，si)_in.z作为测试用例最多运行sum^*次pfsm^*则必有输出序列yk1.yk2…ykn.yij^*，即输入序列path(s0，si)_in.z运行在pfsm与pfsm^*上的输出不一致，即最多运行sum^*次输入序列path(s0，si)_in.z可杀死变异体pfsm^*；其中而p1＝pk1×pk2×…×pkn；

用一个二元组<path(s0，si)_in.？，sum^*>表示最多运行sum^*次输入序列path(s0，si)_in.？可杀死在pfsm中增加了以状态si为起始以？为输入的变异体pfsm^*并确定所增加输入的测试用例，则用于杀死基于pfsm增加输入的变异体的测试用例集πin_extra＝{<path(s0，si)_in.？，sum^*>|i为pfsm任意状态si的下标值，？为以状态si为起始迁移的新增输入}。

还包括迁移丢失，针对迁移丢失的变异操作：

设在概率有限状态机pfsm中，以状态si为起始且输入为xi1的迁移分别为：(si，xi1，yi1，si1，pi1)，(si，xi1，yi2，si2，pi2)，...，(si，xi1，yim，sim，pim)而在其变异体pfsm^*中以状态si为起始且输入为xi1的迁移分别为：(si，xi1，yi1，si1，pi1^*)，(si，xi1，yi2，si2，pi2^*)，...，(si，xi1，yi(j-1)，si(j-1)，pi(j-1)^*)，(si，xi1，yi(j+1)，si(j+1)，pi(j+1)^*)，...，(si，xi1，yim，sim，pim^*)，即原pfsm丢失了迁移(si，xi1，yij，sij，pij)，则pfsm^*为基于迁移丢失的变异体，其中

若要检测以状态si为起始且以x为输入的迁移是否丢失，则需要在变异体运行3.8416p(1-p)/ξ²次path(s0，si)_in.x，其中p为从初始状态转移到状态si的转移概率；

用二元组<path(s0，si)_in.x，3.8416p(1-p)/ξ²>表示最多运行3.8416p(1-p)/ξ²次输入序列path(s0，si)_in.x可杀死基于迁移丢失的变异体pfsm^*并确定所改变输入的测试用例；则基于迁移丢失的测试用例集πtran_lose＝{<path(s0，si)_in.xij，3.8416p(1-p)/ξ²>|i为pfsm任意状态si的下标值，xij为以状态si为起始迁移的输入}。

一种电子设备，其中，包括：至少一个处理器，与所述至少一个处理器通信连接的存储器、显示器和输入器，所述存储器存储有可被所述至少一个处理器执行的任一所述的概率有限状态机变异测试用例生成方法以及用到的数据，所述显示器输出所述至少一个处理器的执行结果，所述输入器输入用户的操作指令。

本发明至少包括以下有益效果：

本发明的方法得到的测试用例能够有效地杀死变异体，变异充分度高；同时由于对每个变异体无需判定其是否与原pfsm等价，因此测试时间少，尤其是随着pfsm规模及变异体个数的增加，相比文献17中r.m.hierons，m.g.merayo提出的基于等价判定的方法，本发明所提出的方法优势更明显，而且能够确定变异体的变异原因及位置。

本发明的其它优点、目标和特征将部分通过下面的说明体现，部分还将通过对本发明的研究和实践而为本领域的技术人员所理解。

附图说明

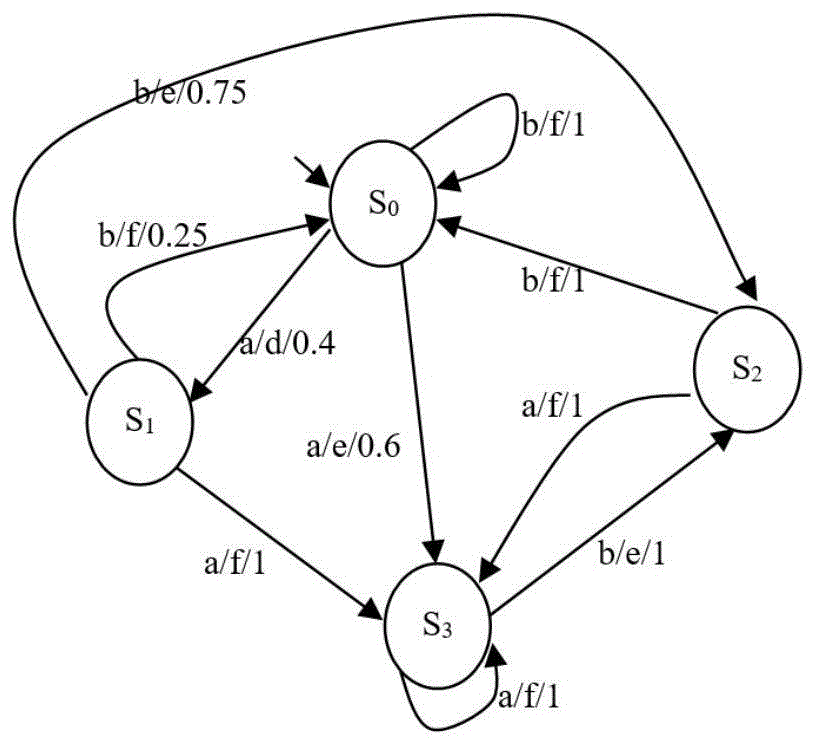
图1为本发明的概率有限状态机pfsm示意图；

图2为本发明的原始有限状态机fsm示意图；

图3为本发明的基于改变迁移目标状态的变异体示意图；

图4为本发明的基于改变概率的变异体示意图；

图5为本发明的基于迁移丢失的变异体示意图；

图6为本发明的基于改变输入的变异体示意图；

图7为本发明的基于增加输入的变异体示意图；

图8为本发明的pfsm各类变异体被杀死数目；

图9为本发明pfsm各类变异体测试时间；

图10为本发明的另一种概率有限状态机pfsm示意图；

图11为本发明图10的pfsm各类变异体被杀死数目；

图12为本发明图10的pfsm各类变异体测试时间；

图13为本发明中两种方法对基于改变概率的变异体测试时间比较；

图14为本发明中两种方法对基于改变迁移目标状态的变异体测试时间比较。

具体实施方式

下面结合实施例对本发明做进一步的详细说明，以令本领域技术人员参照说明书文字能够据以实施。

本发明的设计方案如下：

针对概率有限状态机(probabilisticfinitestatemachine，简称pfsm)变异测试问题，定义了包括改变概率、改变初始状态、改变迁移目标状态、迁移丢失、增加输入等变异操作；在定义pfsm原始状态机基础上，根据各种变异操作的特点，利用pfsm原始状态机的测试用例集和假设检验理论提出杀死各种变异体的测试用例生成方法。

定义1：概率有限状态机pfsm是一个五元组(s，s0，x，y，h)，其中s是一个有限状态集；s0∈s为状态机的初始状态；x是一个有限输入符号集；y是一个有限输出符号集；h:s×x→s×y×(0，1]为迁移关系函数；设s1，s2∈s，x∈x且y∈y，用(s1，x，y，s2，p)表示在状态s1下，当输入为x，则输出为y且从状态s1转移到状态s2的概率为p；同时满足对每个s∈s，x∈x都有其中p(s,x,y,s^*)为当pfsm在状态s下输入x时转移到s^*且输出y的概率。

定义2：设概率有限状态机pfsm＝(s，s0，x，y，h)，定义函数pm:s×x→s×y×(0，1]如下：

定义3：设概率有限状态机pfsm＝(s，s0，x，y，h)，而且从状态si始在输入序列的作用下，输出为而且转移到状态sj的概率p^*m(si，xx，yy，其中：

定义4：设概率有限状态机pfsm＝(s，s0，x，y，h)，则称fsm＝(s，s0，x，y，h-p)为pfsm的原始有限状态机，其中h-p为s×x→s×y，且fsm中存在迁移(s1，a，b，s2)当且仅当在pfsm中存在(s1，a，b，s2，p)。

基于wp方法的有限状态机测试用例生成算法可求出如下相关数据：

(1)状态机各个状态s0，s1，…，sn-1的状态识别集合w0，w1，…，wn-1；(2)使状态机从初始状态转移到各个状态的输入序列集合即状态覆盖集合q＝{in0i|in0i为使状态机从初始状态转移到各状态的输入序列}；(3)迁移覆盖集合p；(4)测试用例集π。

1.概率有限状态机的变异操作及其测试用例生成

1.1改变概率

定义5：设在概率有限状态机pfsm中，以状态si为起始且输入为xi1的迁移分别为：(si，xi1，yi1，si1，pi1)，(si，xi1，yi2，si2，pi2)，...，(si，xi1，yim，sim，pim)而在其变异体pfsm^*中以状态si为起始且输入为xi1的迁移分别为：(si，xi1，yi1，si1，pi1^*)，(si，xi1，yi2，si2，pi2^*)，…(si，xi1，yim，sim，pim^*)，并且至少pfsm中存在迁移(si，xi1，yij，sij，pij)而pfsm^*中存在迁移(si，xi1，yij，sij，pij^*)使得pij≠pij^*(1≤j≤m)，则称pfsm^*为pfsm基于改变概率出的变异体，其中

由于在pfsm的原始状态机存在in0i∈q，因此在pfsm中存在从状态s0到si的一条路径path(s0，si)，设其所经历的迁移序列如下：

为了能够检测出pfsm^*中的迁移(si，xi1，yij，sij，pij^*)与pfsm中的迁移(si，xi1，yij，sij，pij)满足pij≠pij^*，需要通过测试表明：当被测的pfsm^*处于状态si且输入xi1时，输出yij的概率不等于pij；根据概率统计方法，可通过多次考察当被测的pfsm^*处于状态si当输入xi1时输出yij的次数来实现概率值的计算。如果状态si为初始状态，则以xi1作为输入多次运行状态机并记下输出yij的次数即可求出其概率值。若si不是初始状态，则首先使状态机从初始状态转移到状态si，然后才能输入xi1并进行统计；利用path(s0，si)_in输入序列可使状态机从初始状态转移到状态si，但在状态机中可能存在path(s0，si)_in＝path(s0，sj)_in，即把path(s0，si)_in运行于状态机，状态可能转移到si或s；本发明所讨论的状态机是精简的，若path(s0，si)_in作用于状态机的输出序列为path(s0，si)_out则状态机必转移到si。为此，以path(s0，si)_in.xi1作为输入运行于pfsm^*若干次并统计输出序列的子串(该子串为输出序列除掉最后一个字符的字符串)等于path(s0，si)_out且输出序列最后一个字符为yij的次数sumij，即当pfsm^*处于状态si且输入xi1时输出yij的次数。

根据假设检验方法可知，若允许pij与pij^*的误差在ξ之间，即满足pij-ξ<pij^*<pij+ξ，则在path(s0，si)_in作用下到达状态si的样本数sum^*需满足下式

其中p＝pk1×pk2×...×pkm，若可信度取0.95，则z0＝1.96，由上式可得：

sum^*≥3.8416p(1-p)/ξ²(2)

即当样本数sum^*≥3.8416p(1-p)/ξ²，如果满足pij-ξ<sumij/sum^*<pij+ξ，则得到pij与pij^*一致的结论，否则有pij≠pij^*。

因此，如果pfsm^*中的迁移(si，xi1，yij，sij，pij^*)与pfsm中的迁移(si，xi1，yij，sij，pij)满足pij≠pij^*且误差超过ξ，则当以path(s0，si)_in.xi1作为输入运行于pfsm^*次数达3.8416p(1-p)/ξ²时pij-ξ<sumij/sum^*<pij+ξ不成立，即可杀死变异体pfsm^*；用来判定pfsm^*中的迁移(si，xi1，yij，sij，pij^*)与pfsm中的迁移(si，xi1，yij，sij，pij)是否满足pij≠pij^*的具体步骤见算法1，其中为字符串的最后一个非空字符。

算法1概率不一致判定算法

输入：pfsm^*，path(s0，si)_in.xi1，ξ

输出：flag

1.初始化：sumij＝0，sum^*＝0；

2.若sum^*≥3.8416p(1-p)/ξ²，则转至5，否则以path(s0，si)_in.xi1作为输入序列运行pfsm^*得到输出序列

3.若则sum^*←sum^*+1且转至4，否则转至2；

4.若则sumij←sumij+1且转至2；

5.若pij-ξ<sumij/sum^*<pij+ξ，则flag←1，否则flag←0

用一个二元组<path(s0，si)_in.xi1，sum^*>表示最多运行sum^*次输入序列path(s0，si)_in.xi1可杀死上述所描述变异体pfsm^*并确定所改变概率的测试用例，则用于杀死基于pfsm改变概率的变异体的测试用例集∏pro_change＝{<path(s0，si)_in.xij，sum^*>|i为pfsm任意状态si的下标值，xij为以状态si为起始迁移的输入}，其中sum^*的求解方法为sum^*≥3.8416p(1-p)/ξ²。

1.2改变初始状态

定义6：设概率有限状态机pfsm的初始状态为s0而其变异体pfsm^*的初始状态为si，其中i≠0，即初始状态s0变成si，则称pfsm*为pfsm基于改变初始状态的变异体.

对于pfsm的原始有限状态机fsm，如果其初始状态s0变成si(i≠0)，即得到一个与fsm不同的有限状态机fsm^*，则根据文献[2]的wp方法可知，存在状态s0的识别特征集w0使得(s0，w0)≠(si，w0)，其中(s0，w0)，(si，w0)分别为状态s0，si在w0作用下的输出集合，即w0能杀死fsm^*.下面证明w0也能杀死变异体pfsm^*。

定理1：设概率有限状态机pfsm的初始状态为s0而其变异体pfsm^*的初始状态为si，而且w0为pfsm的原始有限状态机fsm初始状态s0的特征，则w0能杀死变异体pfsm*。

1.3改变迁移目标状态

定义7：设概率有限状态机pfsm的迁移t＝(si，x，y，si，p)在其变异体pfsm^*中为t^*＝(si，x，y，sk，p)，其中j≠k，即迁移t的目标状态si变成sk，则称pfsm*为pfsm基于改变迁移目标状态的变异体。

对于pfsm的原始有限状态机fsm，如果其迁移(si，x，y，si)的目标状态si变成sk，即得到一个与fsm不同的有限状态机，不妨记为fsm^*，则根据文献[28]的结论可知在由wp方法生成的测试用例集π中存在输入序列使得其中分别为fsm，fsm^*在输入序列的作用下产生的一个输出序列。下面证明输入序列也使得即能杀死变异体。

定理2：设概率有限状态机pfsm的迁移t＝(si，x，y，si，p)在其变异体pfsm*中为t^*＝(si，x，y，sk，p)，若在pfsm的原始有限状态机fsm中存在输入序列使得则能杀死变异体pfsm^*。

那么如何在pfsm的原始有限状态机fsm中找到输入序列使得x能杀死变异体pfsm^*，最简单方法就是穷举法，但穷举法要逐一对fsm测试用例集π中的每个输入序列分别作用于fsm和fsm^*并比较所有可能的输出序列是否不同；然而随着状态机规模的增大，π中的输入序列个数及各输入序列的长度将也增加，从而通过穷举法来找杀死变异体pfsm*的测试用例效率变低。本发明给出一种在π中找到杀死变异体的输入序列的有效方法。

由于ω中的输入序列越长则的可能性越大，另一方面其测试的代价也更高，为此可定义输入序列优先值如式(3)：

其中为输入序列的长度，maxlen为ω中最长输入序列的长度值，α∈(0，1)为序列长度在优先值中的权重；ω中优先值大的输入序列将被优先运行于fsm^*以检测该序列是否为杀死变异体的输入序列。杀死变异体的测试序列的具体求解见算法2。

算法2杀死变异体的测试序列求解

输入：pfsm的原始状态机fsm及被变异迁移t＝(si，x，y，si，p)

输出：杀死变异体pfsm^*的测试用例

1.利用wp方法生成测试用例集π

3.对ω中的序列按如下方式进行排序：

若则把排在前面，其中maxlen为ω中最长序列的长度值，

4.对已经排序的ω，从ω的第一个序列开始，把序列分别作用fsm与fsm^*，直到有序列使得

1.4迁移丢失

定义8：设在概率有限状态机pfsm中，以状态si为起始且输入为xi1的迁移分别为：(si，xi1，yi1，si1，pi1)，(si，xi1，yi2，si2，pi2)，...，(si，xi1，yim，sim，pim)而在其变异体pfsm^*中以状态si为起始且输入为xi1的迁移分别为：(si，xi1，yi1，si1，pi1^*)，(si，xi1，yi2，si2，pi2^*)，...，(si，xi1，yi(j-1)，si(j-1)，pi(j-1)^*)，(si，xi1，yi(j+1)，si(j+1)，pi(j+1)^*)，...，(si，xi1，yim，sim，pim^*)，即原pfsm丢失了迁移(si，xi1，yij，sij，pij)，则称pfsm^*为基于迁移丢失的变异体，其中

1.5改变输入

定义9：设pfsm为一概率有限状态机，分别用(si，xi1^*，yi1，si1，pi1)，(si，xi1^*，yi2，si2，pi2)，...，(si，xi1^*，yim，sim，pim)替换pfsm的(si，xi1，yi1，si1，pi1)，(si，xi1，yi2，si2，pi2)，...，(si，xi1，yim，sim，pim)而得到pfsm^*，即以状态si为起始且输入为xi1的迁移被输入xi1^*所替换，则称pfsm^*为pfsm基于改变输入的变异体，其中xi1≠xi1^*。

根据变异操作可知，如果pfsm^*是分别用(si，xi1^*，yi1，si1，pi1)，(si，xi1^*，yi2，si2，pi2)，...，(si，xi1^*，yim，sim，pim)替换pfsm的(si，xi1，yi1，si1，pi1)，(si，xi1，yi2，si2，pi2)，...，(si，xi1，yim，sim，pim)得到的概率有限状态机，则当pfsm^*处于状态si时在xi1作用下的输出为空，即输出字符串的长度为0，而当pfsm处于状态si时在xi1作用下的输出为yi1，yi2，...，yim中的某个字符，其长度为1；为了能够断定概率状态机以状态si为起始且输入为xi1的迁移没有被其它输入所替换，按照假设检验方法，可设定一个很小的ω，只要能够说明当状态机处于状态si时在xi1作用下输出字符串长度为1的概率接近1-ω则可认为以状态si为起始且输入为xi1的迁移没有被其它输入所替换，否则将认为其输入被改变；为此，以path(s0，si)_in.xi1作为测试用例反复运行于pfsm^*，直到每个输出序列的子串(该子串为输出序列除掉最后一个字符的字符串)与path(s0，si)_out相等的次数sum^*≥3.8416ω(1-ω)/ξ²并统计在这些输出序列中其长度为|path(s0，si)_in.xi1|的个数之和(记为sum)，若1-ω-ξ<sum/sum^*<1-ω+ξ，则说明以si为起始状态且输入为xi1的迁移没有被其它输入所替换，否则其输入被改变。

通过上述测试后，如果确认了概率状态机以si为起始状态且输入为xi1的迁移被其它输入所替换，则接下来就要判定替换的是哪个输入字符？设在概率有限状态机pfsm中，以状态si为起始的所有迁移的输入集为x1，我们用path(s0，si)_in与x1中的每个字符x构成的输入序列path(s0，si)_in.x对pfsm^*进行测试，如果是x替换了xi1，则按照上述方法进行测试就会有1-ω-ξ<sum/sum^*<1-ω+ξ，即可知输入xi1被x所替换.因此，即可杀死变异体。

用一个二元组<path(s0，si)_in.xi1，3.8416ω(1-ω)/ξ²>表示最多运行3.8416ω(1-ω)/ξ²次输入序列path(s0，si)_in.xi1可杀死上述所描述变异体pfsm^*并确定所改变输入的测试用例，则用于杀死基于pfsm迁移丢失的变异体的测试用例集πin_change＝{<path(s0，si)_in.xij，3.8416ω(1-ω)/ξ²>|i为pfsm任意状态si的下标值，xij为以状态si为起始迁移的输入}。

1.6增加输入

定义10：设在概率有限状态机pfsm中，以状态si为起始的所有迁移的输入集为x1，若pfsm的变异体pfsm^*以状态si为起始的所有迁移的输入集为x2且则称pfsm^*为pfsm基于增加输入的变异体。

若z∈x2而即增加了输入z，那么当pfsm^*处于状态si时在z作用下输出一个非空的字符，而当pfsm处于状态si时在z作用下则没有字符输出.根据假设检验理论可知，当以path(s0，si)_in.z作为测试用例运行于pfsm的次数最多达到sum^*时必然有输出序列yk1.yk2…ykn，而把path(s0，si)_in.z作为测试用例最多运行sum^*次pfsm^*则必有输出序列yk1.yk2…ykn.yij^*，即输入序列path(s0，si)_in.z运行在pfsm与pfsm^*上的输出不一致，即最多运行sum^*次输入序列path(s0，si)_in.z可杀死变异体pfsm^*.其中而p1＝pk1×pk2×…×pkn。

2.变异测试用例生成例子

下面通过例子来说明如何生成杀死对上述所定义的各类变异体，如图1为一概率有限状态机，共有4个状态和10条迁移，各迁移具体输入、输出及转移概率见图所示；图2则是如图1的原始有限状态机；图3至图9分别是如图1概率有限状态机基于改变迁移目标状态、基于改变概率的变异体、基于迁移丢失、基于改变输入、基于增加输入、基于改变输出的变异体、基于增加输出的变异体。

根据wp方法可得到pfsm原始有限状态机fsm的相关集合：

(1)各个状态识别集w0＝{a}，w1＝{b}，w2＝{a，b}，w3＝{b}，其中wi为状态si的识别集，0≤i≤3；

(2)状态覆盖集q＝{ε，a，a.b}，从初始状态s0转移到状态si并停留在该状态的输入序列的子集其中q0＝{ε}，q1＝{a}，q2＝{a.b}，q3＝{a}；

(3)测试用例集π如下：

π＝{a，b，a.a，a.b，a.b.a，a.b.b，b.a，a.a.b，a.b.a.b，a.b.b.a}。

图3为基于改变迁移目标状态的变异体，原pfsm的迁移(s3，a，f，s3，1)，在变异体中则为(s3，a，f，s2，1)；根据算法2可知ω＝{a.a，a.a.b}，maxlen＝3，设α＝0.4则按公式(3)计算ω中各个序列的优先值如下：pri(a.a)＝1.7，pri(a.a.b)＝1.8，因此首先把a.b.a运行于变异体，其输出序列集合为{d.f.e，e.f.f}，而在pfsm上运行a.b.a的输出序列集合则为{d.f.e，e.f.e}，即a.b.a为杀死变异体的测试用例。

图4是基于改变概率的变异体，即原pfsm的(s1，b，f，s0，0.25)被改成(s1，b，f，s0，0.5)，而(s1，b，e，s2，0.75)被改成(s1，b，e，s2，0.5).根据前文所给的方法可求出测试序列为a.b，若设ξ＝0.01则需测试的次数为3.8416/(0.01)²×0.2×0.8＝6144，即需用测试序列a.b反复运行变异体6144次；运行结果表明输出d.f和d.e共达2460次，其中输出d.f共1221次即概率值为0.496，与pfsm的概率值0.25相差0.246；而输出1239次d.e即概率值为0.504与pfsm的概率值0.75差0.246.可见，概率差值均大于0.01超出了允许的误差范围，即检测出概率被改变了，因此最多运行6147次a.b可杀死变异体。

图5为基于迁移丢失的变异体，即与原pfsm相比少了迁移(s1，b，f，s0，0.25).根据上文的方法可知，若要检测以状态si为起始且以x为输入的迁移是否丢失，则需要在变异体运行3.8416p(1-p)/ξ²次path(s0，si)_in.x，其中p为从初始状态转移到状态si的转移概率，因此用来测试如图1的pfsm是否有迁移丢失的测试用例集πtran_lose＝{<a，9220>，<b，1>，<a.a，9220>，<a.b，7203>，<a.b，9220>，<a.b.a，9220>，<a.b.b，9220>}，其中<a，9220>(<b，1>)用来杀死以状态s0为起始以a(b)为输入的迁移丢失的变异体；<a.a，9220>用来杀死丢失了以状态s1或s3为起始以a为输入的迁移的变异体；<a.b，7203>(<a.b，9220>)用来杀死以状态s1(s3)为起始以b为输入的迁移丢失的变异体；<a.b.a，9220>(<a.b.b，9220>)用来杀死以状态s2为起始以a(b)为输入的迁移丢失的变异体.当用输入序列a.b运行于如图5的变异体7203次，结果在7203个输出序列中第一个字符为d的序列共有2883个，其中第一个字符为d且第二个字符为f的序列为0个，而第一个字符为d且第二个字符为e的序列为2883个；而当用输入序列a.b运行于如图1的概率状态机7203次时，结果在7203个输出序列中第一个字符为d的序列共有2885个，其中第一个字符为d且第二个字符为f的序列为720个，而第一个字符为d且第二个字符为e的序列为2165个；因此可知丢失了迁移(s1，b，f，s0，0.25)。

图6是基于改变输入的变异体，即原pfsm的(s1，b，e，s2，0.75)被改成了迁移(s1，a，e，s2，0.5)，即输入b改成了a；设ξ＝ω＝0.01，则根据上文1.5所给的方法可知：

πin_change＝{<a，383>，<b，383>，<a.a，383>，<a.b，383>，<a.b，383>，<a.b.a，383>，<a.b.b，383>}。运用<a.b，383>对变异体测试，输出的字符串中，第一个字符为d的字符串只有d.f而没有d.e，进一步利用<a.a，383>对变异体测试其输出除了有d.f外还有d.e，因此可知原pfsm的(s1，b，e，s2，0.75)输入b被改成了a，即所给测试用例能杀死变异体。

图7是基于增加输入的变异体，与原pfsm的相比，变异体多了迁移(s1，c，e，s3，1)，即导致增加了输入e。设ξ＝0.01，则根据上文1.6所给的方法可知πin_extra＝{<？，1>，<a.？，9220>，<a.b.？，7203>}，其中<？，1>用来杀死以状态s0为起始且输入为？的迁移的变异体；<a.？，9220>用来杀死以状态s1，s3为起始且输入为？的迁移的变异体；<a.b.？，7203>用来杀死以状态s2为起始且输入为？的迁移的变异体；？为除a，b以外的输入符.若要杀死有输入为c的迁移的变异体，则用c替换？即可得到杀死变异体的测试用例。例如，对图1的pfsm实施测试用例<a.c，7203>的输出有d和e，而对图7的变异体实施该用例时其输出则为d.e和e，变异体上的输出与在原体上的输出不一致，因此测试用例<a.c，7203>可杀死如图7的变异体。

程序设计例